First-Class Functions
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Programming Languages
Programming Languages Recitation Summer 2014 Recitation Leader • Joanna Gilberti • Email: [email protected] • Office: WWH, Room 328 • Web site: http://cims.nyu.edu/~jlg204/courses/PL/index.html Homework Submission Guidelines • Submit all homework to me via email (at [email protected] only) on the due date. • Email subject: “PL– homework #” (EXAMPLE: “PL – Homework 1”) • Use file naming convention on all attachments: “firstname_lastname_hw_#” (example: "joanna_gilberti_hw_1") • In the case multiple files are being submitted, package all files into a ZIP file, and name the ZIP file using the naming convention above. What’s Covered in Recitation • Homework Solutions • Questions on the homeworks • For additional questions on assignments, it is best to contact me via email. • I will hold office hours (time will be posted on the recitation Web site) • Run sample programs that demonstrate concepts covered in class Iterative Languages Scoping • Sample Languages • C: static-scoping • Perl: static and dynamic-scoping (use to be only dynamic scoping) • Both gcc (to run C programs), and perl (to run Perl programs) are installed on the cims servers • Must compile the C program with gcc, and then run the generated executable • Must include the path to the perl executable in the perl script Basic Scope Concepts in C • block scope (nested scope) • run scope_levels.c (sl) • ** block scope: set of statements enclosed in braces {}, and variables declared within a block has block scope and is active and accessible from its declaration to the end of the block -

Chapter 5 Names, Bindings, and Scopes
Chapter 5 Names, Bindings, and Scopes 5.1 Introduction 198 5.2 Names 199 5.3 Variables 200 5.4 The Concept of Binding 203 5.5 Scope 211 5.6 Scope and Lifetime 222 5.7 Referencing Environments 223 5.8 Named Constants 224 Summary • Review Questions • Problem Set • Programming Exercises 227 CMPS401 Class Notes (Chap05) Page 1 / 20 Dr. Kuo-pao Yang Chapter 5 Names, Bindings, and Scopes 5.1 Introduction 198 Imperative languages are abstractions of von Neumann architecture – Memory: stores both instructions and data – Processor: provides operations for modifying the contents of memory Variables are characterized by a collection of properties or attributes – The most important of which is type, a fundamental concept in programming languages – To design a type, must consider scope, lifetime, type checking, initialization, and type compatibility 5.2 Names 199 5.2.1 Design issues The following are the primary design issues for names: – Maximum length? – Are names case sensitive? – Are special words reserved words or keywords? 5.2.2 Name Forms A name is a string of characters used to identify some entity in a program. Length – If too short, they cannot be connotative – Language examples: . FORTRAN I: maximum 6 . COBOL: maximum 30 . C99: no limit but only the first 63 are significant; also, external names are limited to a maximum of 31 . C# and Java: no limit, and all characters are significant . C++: no limit, but implementers often impose a length limitation because they do not want the symbol table in which identifiers are stored during compilation to be too large and also to simplify the maintenance of that table. -

Introduction to Programming in Lisp
Introduction to Programming in Lisp Supplementary handout for 4th Year AI lectures · D W Murray · Hilary 1991 1 Background There are two widely used languages for AI, viz. Lisp and Prolog. The latter is the language for Logic Programming, but much of the remainder of the work is programmed in Lisp. Lisp is the general language for AI because it allows us to manipulate symbols and ideas in a commonsense manner. Lisp is an acronym for List Processing, a reference to the basic syntax of the language and aim of the language. The earliest list processing language was in fact IPL developed in the mid 1950’s by Simon, Newell and Shaw. Lisp itself was conceived by John McCarthy and students in the late 1950’s for use in the newly-named field of artificial intelligence. It caught on quickly in MIT’s AI Project, was implemented on the IBM 704 and by 1962 to spread through other AI groups. AI is still the largest application area for the language, but the removal of many of the flaws of early versions of the language have resulted in its gaining somewhat wider acceptance. One snag with Lisp is that although it started out as a very pure language based on mathematic logic, practical pressures mean that it has grown. There were many dialects which threaten the unity of the language, but recently there was a concerted effort to develop a more standard Lisp, viz. Common Lisp. Other Lisps you may hear of are FranzLisp, MacLisp, InterLisp, Cambridge Lisp, Le Lisp, ... Some good things about Lisp are: • Lisp is an early example of an interpreted language (though it can be compiled). -

Scope in Fortran 90
Scope in Fortran 90 The scope of objects (variables, named constants, subprograms) within a program is the portion of the program in which the object is visible (can be use and, if it is a variable, modified). It is important to understand the scope of objects not only so that we know where to define an object we wish to use, but also what portion of a program unit is effected when, for example, a variable is changed, and, what errors might occur when using identifiers declared in other program sections. Objects declared in a program unit (a main program section, module, or external subprogram) are visible throughout that program unit, including any internal subprograms it hosts. Such objects are said to be global. Objects are not visible between program units. This is illustrated in Figure 1. Figure 1: The figure shows three program units. Main program unit Main is a host to the internal function F1. The module program unit Mod is a host to internal function F2. The external subroutine Sub hosts internal function F3. Objects declared inside a program unit are global; they are visible anywhere in the program unit including in any internal subprograms that it hosts. Objects in one program unit are not visible in another program unit, for example variable X and function F3 are not visible to the module program unit Mod. Objects in the module Mod can be imported to the main program section via the USE statement, see later in this section. Data declared in an internal subprogram is only visible to that subprogram; i.e. -

Programming Language Concepts/Binding and Scope
Programming Language Concepts/Binding and Scope Programming Language Concepts/Binding and Scope Onur Tolga S¸ehito˘glu Bilgisayar M¨uhendisli˘gi 11 Mart 2008 Programming Language Concepts/Binding and Scope Outline 1 Binding 6 Declarations 2 Environment Definitions and Declarations 3 Block Structure Sequential Declarations Monolithic block structure Collateral Declarations Flat block structure Recursive declarations Nested block structure Recursive Collateral Declarations 4 Hiding Block Expressions 5 Static vs Dynamic Scope/Binding Block Commands Static binding Block Declarations Dynamic binding 7 Summary Programming Language Concepts/Binding and Scope Binding Binding Most important feature of high level languages: programmers able to give names to program entities (variable, constant, function, type, ...). These names are called identifiers. Programming Language Concepts/Binding and Scope Binding Binding Most important feature of high level languages: programmers able to give names to program entities (variable, constant, function, type, ...). These names are called identifiers. definition of an identifier ⇆ used position of an identifier. Formally: binding occurrence ⇆ applied occurrence. Programming Language Concepts/Binding and Scope Binding Binding Most important feature of high level languages: programmers able to give names to program entities (variable, constant, function, type, ...). These names are called identifiers. definition of an identifier ⇆ used position of an identifier. Formally: binding occurrence ⇆ applied occurrence. Identifiers are declared once, used n times. Programming Language Concepts/Binding and Scope Binding Binding Most important feature of high level languages: programmers able to give names to program entities (variable, constant, function, type, ...). These names are called identifiers. definition of an identifier ⇆ used position of an identifier. Formally: binding occurrence ⇆ applied occurrence. Identifiers are declared once, used n times. -

Names, Scopes, and Bindings (Cont.)
Chapter 3:: Names, Scopes, and Bindings (cont.) Programming Language Pragmatics Michael L. Scott Copyright © 2005 Elsevier Review • What is a regular expression ? • What is a context-free grammar ? • What is BNF ? • What is a derivation ? • What is a parse ? • What are terminals/non-terminals/start symbol ? • What is Kleene star and how is it denoted ? • What is binding ? Copyright © 2005 Elsevier Review • What is early/late binding with respect to OOP and Java in particular ? • What is scope ? • What is lifetime? • What is the “general” basic relationship between compile time/run time and efficiency/flexibility ? • What is the purpose of scope rules ? • What is central to recursion ? Copyright © 2005 Elsevier 1 Lifetime and Storage Management • Maintenance of stack is responsibility of calling sequence and subroutine prolog and epilog – space is saved by putting as much in the prolog and epilog as possible – time may be saved by • putting stuff in the caller instead or • combining what's known in both places (interprocedural optimization) Copyright © 2005 Elsevier Lifetime and Storage Management • Heap for dynamic allocation Copyright © 2005 Elsevier Scope Rules •A scope is a program section of maximal size in which no bindings change, or at least in which no re-declarations are permitted (see below) • In most languages with subroutines, we OPEN a new scope on subroutine entry: – create bindings for new local variables, – deactivate bindings for global variables that are re- declared (these variable are said to have a "hole" in their -

Class 15: Implementing Scope in Function Calls
Class 15: Implementing Scope in Function Calls SI 413 - Programming Languages and Implementation Dr. Daniel S. Roche United States Naval Academy Fall 2011 Roche (USNA) SI413 - Class 15 Fall 2011 1 / 10 Implementing Dynamic Scope For dynamic scope, we need a stack of bindings for every name. These are stored in a Central Reference Table. This primarily consists of a mapping from a name to a stack of values. The Central Reference Table may also contain a stack of sets, each containing identifiers that are in the current scope. This tells us which values to pop when we come to an end-of-scope. Roche (USNA) SI413 - Class 15 Fall 2011 2 / 10 Example: Central Reference Tables with Lambdas { new x := 0; new i := -1; new g := lambda z{ ret :=i;}; new f := lambda p{ new i :=x; i f (i>0){ ret :=p(0); } e l s e { x :=x + 1; i := 3; ret :=f(g); } }; w r i t e f( lambda y{ret := 0}); } What gets printed by this (dynamically-scoped) SPL program? Roche (USNA) SI413 - Class 15 Fall 2011 3 / 10 (dynamic scope, shallow binding) (dynamic scope, deep binding) (lexical scope) Example: Central Reference Tables with Lambdas The i in new g := lambda z{ w r i t e i;}; from the previous program could be: The i in scope when the function is actually called. The i in scope when g is passed as p to f The i in scope when g is defined Roche (USNA) SI413 - Class 15 Fall 2011 4 / 10 Example: Central Reference Tables with Lambdas The i in new g := lambda z{ w r i t e i;}; from the previous program could be: The i in scope when the function is actually called. -

Javascript Scope Lab Solution Review (In-Class) Remember That Javascript Has First-Class Functions
C152 – Programming Language Paradigms Prof. Tom Austin, Fall 2014 JavaScript Scope Lab Solution Review (in-class) Remember that JavaScript has first-class functions. function makeAdder(x) { return function (y) { return x + y; } } var addOne = makeAdder(1); console.log(addOne(10)); Warm up exercise: Create a makeListOfAdders function. input: a list of numbers returns: a list of adders function makeListOfAdders(lst) { var arr = []; for (var i=0; i<lst.length; i++) { var n = lst[i]; arr[i] = function(x) { return x + n; } } return arr; } Prints: 121 var adders = 121 makeListOfAdders([1,3,99,21]); 121 adders.forEach(function(adder) { 121 console.log(adder(100)); }); function makeListOfAdders(lst) { var arr = []; for (var i=0; i<lst.length; i++) { arr[i]=function(x) {return x + lst[i];} } return arr; } Prints: var adders = NaN makeListOfAdders([1,3,99,21]); NaN adders.forEach(function(adder) { NaN console.log(adder(100)); NaN }); What is going on in this wacky language???!!! JavaScript does not have block scope. So while you see: for (var i=0; i<lst.length; i++) var n = lst[i]; the interpreter sees: var i, n; for (i=0; i<lst.length; i++) n = lst[i]; In JavaScript, this is known as variable hoisting. Faking block scope function makeListOfAdders(lst) { var i, arr = []; for (i=0; i<lst.length; i++) { (function() { Function creates var n = lst[i]; new scope arr[i] = function(x) {return x + n;} })(); } return arr; } A JavaScript constructor name = "Monty"; function Rabbit(name) { this.name = name; } var r = Rabbit("Python"); Forgot new console.log(r.name); -

A History of Clojure
A History of Clojure RICH HICKEY, Cognitect, Inc., USA Shepherd: Mira Mezini, Technische Universität Darmstadt, Germany Clojure was designed to be a general-purpose, practical functional language, suitable for use by professionals wherever its host language, e.g., Java, would be. Initially designed in 2005 and released in 2007, Clojure is a dialect of Lisp, but is not a direct descendant of any prior Lisp. It complements programming with pure functions of immutable data with concurrency-safe state management constructs that support writing correct multithreaded programs without the complexity of mutex locks. Clojure is intentionally hosted, in that it compiles to and runs on the runtime of another language, such as the JVM. This is more than an implementation strategy; numerous features ensure that programs written in Clojure can leverage and interoperate with the libraries of the host language directly and efficiently. In spite of combining two (at the time) rather unpopular ideas, functional programming and Lisp, Clojure has since seen adoption in industries as diverse as finance, climate science, retail, databases, analytics, publishing, healthcare, advertising and genomics, and by consultancies and startups worldwide, much to the career-altering surprise of its author. Most of the ideas in Clojure were not novel, but their combination puts Clojure in a unique spot in language design (functional, hosted, Lisp). This paper recounts the motivation behind the initial development of Clojure and the rationale for various design decisions and language constructs. It then covers its evolution subsequent to release and adoption. CCS Concepts: • Software and its engineering ! General programming languages; • Social and pro- fessional topics ! History of programming languages. -
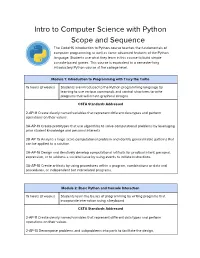
Intro to Computer Science with Python Scope and Sequence
Intro to Computer Science with Python Scope and Sequence The CodeHS introduction to Python course teaches the fundamentals of computer programming as well as some advanced features of the Python language. Students use what they learn in this course to build simple console-based games. This course is equivalent to a semester-long introductory Python course at the college level. Module 1: Introduction to Programming with Tracy the Turtle 15 hours (3 weeks) Students are introduced to the Python programming language by learning to use various commands and control structures to write programs that will create graphical designs. CSTA Standards Addressed 2-AP-11 Create clearly named variables that represent different data types and perform operations on their values. 3A-AP-13 Create prototypes that use algorithms to solve computational problems by leveraging prior student knowledge and personal interests. 3B-AP-15 Analyze a large-scale computational problem and identify generalizable patterns that can be applied to a solution. 3A-AP-16 Design and iteratively develop computational artifacts for practical intent, personal, expression, or to address a societal issue by using events to initiate instructions. 3A-AP-18 Create artifacts by using procedures within a program, combinations or data and procedures, or independent but interrelated programs. Module 2: Basic Python and Console Interaction 15 hours (3 weeks) Students learn the basics of programming by writing programs that incorporate interaction using a keyboard. CSTA Standards Addressed 2-AP-11 Create clearly named variables that represent different data types and perform operations on their values. 2-AP-13 Decompose problems and subproblems into parts to facilitate the design, implementation, and review of programs 3B-AP-15 Analyze a large-scale computational problem and identify generalizable patterns that can be applied to a solution. -

Software II: Principles of Programming Languages Introduction
Software II: Principles of Programming Languages Lecture 5 – Names, Bindings, and Scopes Introduction • Imperative languages are abstractions of von Neumann architecture – Memory – Processor • Variables are characterized by attributes – To design a type, must consider scope, lifetime, type checking, initialization, and type compatibility Names • Design issues for names: – Are names case sensitive? – Are special words reserved words or keywords? Names (continued) • Length – If too short, they cannot be connotative – Language examples: • FORTRAN 95: maximum of 31 (only 6 in FORTRAN IV) • C99: no limit but only the first 63 are significant; also, external names are limited to a maximum of 31 (only 8 are significant K&R C ) • C#, Ada, and Java: no limit, and all are significant • C++: no limit, but implementers often impose one Names (continued) • Special characters – PHP: all variable names must begin with dollar signs – Perl: all variable names begin with special characters, which specify the variable’s type – Ruby: variable names that begin with @ are instance variables; those that begin with @@ are class variables Names (continued) • Case sensitivity – Disadvantage: readability (names that look alike are different) • Names in the C-based languages are case sensitive • Names in others are not • Worse in C++, Java, and C# because predefined names are mixed case (e.g. IndexOutOfBoundsException ) Names (continued) • Special words – An aid to readability; used to delimit or separate statement clauses • A keyword is a word that is special only -

Down with Emacs Lisp: Dynamic Scope Analysis
Down with Emacs Lisp: Dynamic Scope Analysis Matthias Neubauer Michael Sperber Institut fur¨ Informatik Wilhelm-Schickard-Institut fur¨ Informatik Universitat¨ Freiburg Universitat¨ Tubingen¨ [email protected] [email protected] ABSTRACT comparatively little focus on significant improvements of the It is possible to translate code written in Emacs Lisp or an- Emacs Lisp interpreter. other Lisp dialect which uses dynamic scoping to a more On the other hand, recent years have seen the advent modern programming language with lexical scoping while of a large number of extension language implementations largely preserving structure and readability of the code. The of full programming languages suitable for the inclusion in biggest obstacle to such an idiomatic translation from Emacs application software. Specifically, several current Scheme Lisp is the translation of dynamic binding into suitable in- implementations are technologically much better suited as stances of lexical binding: Many binding constructs in real an extension language for Emacs than Emacs Lisp itself. programs in fact exhibit identical behavior under both dy- In fact, the official long-range plan for GNU Emacs is to namic and lexical binding. An idiomatic translation needs to replace the Emacs Lisp substrate with Guile, also a Scheme detect as many of these binding constructs as possible and implementation [28]. The work presented here is part of a convert them into lexical binding constructs in the target different, independent effort to do the same for XEmacs, a language to achieve readability and efficiency of the target variant of GNU Emacs which also uses Emacs Lisp as its code.