Lecture 4: Particles in a 2D Box, Degeneracy, Harmonic Oscillator
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Study of Fractional Schrödinger Equation-Composed Via Jumarie Fractional Derivative
A Study of Fractional Schrödinger Equation-composed via Jumarie fractional derivative Joydip Banerjee1, Uttam Ghosh2a , Susmita Sarkar2b and Shantanu Das3 Uttar Buincha Kajal Hari Primary school, Fulia, Nadia, West Bengal, India email- [email protected] 2Department of Applied Mathematics, University of Calcutta, Kolkata, India; 2aemail : [email protected] 2b email : [email protected] 3 Reactor Control Division BARC Mumbai India email : [email protected] Abstract One of the motivations for using fractional calculus in physical systems is due to fact that many times, in the space and time variables we are dealing which exhibit coarse-grained phenomena, meaning that infinitesimal quantities cannot be placed arbitrarily to zero-rather they are non-zero with a minimum length. Especially when we are dealing in microscopic to mesoscopic level of systems. Meaning if we denote x the point in space andt as point in time; then the differentials dx (and dt ) cannot be taken to limit zero, rather it has spread. A way to take this into account is to use infinitesimal quantities as ()Δx α (and ()Δt α ) with 01<α <, which for very-very small Δx (and Δt ); that is trending towards zero, these ‘fractional’ differentials are greater that Δx (and Δt ). That is()Δx α >Δx . This way defining the differentials-or rather fractional differentials makes us to use fractional derivatives in the study of dynamic systems. In fractional calculus the fractional order trigonometric functions play important role. The Mittag-Leffler function which plays important role in the field of fractional calculus; and the fractional order trigonometric functions are defined using this Mittag-Leffler function. -

Lecture 16 Matter Waves & Wave Functions
LECTURE 16 MATTER WAVES & WAVE FUNCTIONS Instructor: Kazumi Tolich Lecture 16 2 ¨ Reading chapter 34-5 to 34-8 & 34-10 ¤ Electrons and matter waves n The de Broglie hypothesis n Electron interference and diffraction ¤ Wave-particle duality ¤ Standing waves and energy quantization ¤ Wave function ¤ Uncertainty principle ¤ A particle in a box n Standing wave functions de Broglie hypothesis 3 ¨ In 1924 Louis de Broglie hypothesized: ¤ Since light exhibits particle-like properties and act as a photon, particles could exhibit wave-like properties and have a definite wavelength. ¨ The wavelength and frequency of matter: # & � = , and � = $ # ¤ For macroscopic objects, de Broglie wavelength is too small to be observed. Example 1 4 ¨ One of the smallest composite microscopic particles we could imagine using in an experiment would be a particle of smoke or soot. These are about 1 µm in diameter, barely at the resolution limit of most microscopes. A particle of this size with the density of carbon has a mass of about 10-18 kg. What is the de Broglie wavelength for such a particle, if it is moving slowly at 1 mm/s? Diffraction of matter 5 ¨ In 1927, C. J. Davisson and L. H. Germer first observed the diffraction of electron waves using electrons scattered from a particular nickel crystal. ¨ G. P. Thomson (son of J. J. Thomson who discovered electrons) showed electron diffraction when the electrons pass through a thin metal foils. ¨ Diffraction has been seen for neutrons, hydrogen atoms, alpha particles, and complicated molecules. ¨ In all cases, the measured λ matched de Broglie’s prediction. X-ray diffraction electron diffraction neutron diffraction Interference of matter 6 ¨ If the wavelengths are made long enough (by using very slow moving particles), interference patters of particles can be observed. -

Particle-On-A-Ring” Suppose a Diatomic Molecule Rotates in Such a Way That the Vibration of the Bond Is Unaffected by the Rotation
University of Washington Department of Chemistry Chemistry 453 Winter Quarter 2015 Lecture 17 2/25/15 Recommended Reading Atkins & DePaula 9.5 A. Background in Rotational Mechanics Two masses m1 and m2 connected by a weightless rigid “bond” of length r rotates with angular velocity rv where v is the linear velocity. As with vibrations we can render this rotation motion in simpler form by fixing one end of the bond to the origin terminating the other end with reduced mass , and allowing the reduced mass to rotate freely For two masses m1 and m2 separated by r the center of mass (CoM) is defined by the condition mr11 mr 2 2 (17.1) where m2,1 rr1,2 mm12 (17.2) Figure 17.1: Location of center of mass (CoM0 for two masses separated by a distance r. The moment of inertia I plays the role in the rotational energy that is played by mass in translational energy. The moment of inertia is 22 I mr11 mr 2 2 (17.3) Putting 17.3 into 17.4 we obtain I r 2 (17.4) mm where 12 . mm12 We can express the rotational kinetic energy K in terms of the angular momentum. The angular momentum is defined in terms of the cross product between the position vector r and the linear momentum vector p: Lrp (17.5) prprvrsin where the angle between p and r is ninety degrees for circular motion. As a cross product, the angular momentum vector L is perpendicular to the plane defined by the r and p vectors as shown in Figure 17.2 We can use equation 17.6 to obtain an expression for the kinetic energy in terms of the angular momentum L: Figure 17.2: The angular momentum L is a cross product of the position r vector and the linear momentum p=mv vector. -

Dirac Particle in a Square Well and in a Box
Dirac particle in a square well and in a box A. D. Alhaidari Saudi Center for Theoretical Physics, Dhahran, Saudi Arabia We obtain an exact solution of the 1D Dirac equation for a square well potential of depth greater then twice the particle’s mass. The energy spectrum formula in the Klein zone is surprisingly very simple and independent of the depth of the well. This implies that the same solution is also valid for the potential box (infinitely deep well). In the nonrelativistic limit, the well-known energy spectrum of a particle in a box is obtained. We also provide in tabular form the elements of the complete solution space of the problem for all energies. PACS numbers: 03.65.Pm, 03.65.Ge, 03.65.Nk Keywords: Dirac equation, square well, potential box, energy spectrum, Klein paradox Aside from the mathematically “trivial” free case, particle in a box is usually the first problem that an undergraduate student of nonrelativistic quantum mechanics is asked to solve. Normally, he goes further into obtaining the bound states solution of a particle in a finite square well. It is much later that he works out more involved exercises like the 3D Coulomb problem [1]. Unfortunately, in relativistic quantum mechanics the story is reversed. One can hardly find a textbook on relativistic quantum mechanics where the 1D problem of a particle in a potential box is solved before the relativistic Hydrogen atom is [2]. The difficulty is that if this is to be done from the start, then one is forced to get into subtle issues like the Klein paradox, electron-positron pair production, stability of the vacuum, appropriate boundary conditions, …etc. -

Aromaticity As a Guiding Concept for Spectroscopic Features and Nonlinear Optical Properties of Porphyrinoids
molecules Article Aromaticity as a Guiding Concept for Spectroscopic Features and Nonlinear Optical Properties of Porphyrinoids Tatiana Woller 1, Paul Geerlings 1, Frank De Proft 1, Benoît Champagne 2 ID and Mercedes Alonso 1,* ID 1 Eenheid Algemene Chemie (ALGC), Vrije Universiteit Brussel (VUB), Pleinlaan 2, 1050 Brussels, Belgium; [email protected] (T.W.); [email protected] (P.G.); [email protected] (F.D.P.) 2 Laboratoire de Chimie Théorique, Unité de Chimie Physique Théorique et Structurale, University of Namur, Rue de Bruxelles 61, B-5000 Namur, Belgium; [email protected] * Correspondence: [email protected] Academic Editors: Luis R. Domingo and Miquel Solà Received: 5 March 2018; Accepted: 24 May 2018; Published: 1 June 2018 Abstract: With their versatile molecular topology and aromaticity, porphyrinoid systems combine remarkable chemistry with interesting photophysical properties and nonlinear optical properties. Hence, the field of application of porphyrinoids is very broad ranging from near-infrared dyes to opto-electronic materials. From previous experimental studies, aromaticity emerges as an important concept in determining the photophysical properties and two-photon absorption cross sections of porphyrinoids. Despite a considerable number of studies on porphyrinoids, few investigate the relationship between aromaticity, UV/vis absorption spectra and nonlinear properties. To assess such structure-property relationships, we performed a computational study focusing on a series of Hückel porphyrinoids to: (i) assess their (anti)aromatic character; (ii) determine the fingerprints of aromaticity on the UV/vis spectra; (iii) evaluate the role of aromaticity on the NLO properties. Using an extensive set of aromaticity descriptors based on energetic, magnetic, structural, reactivity and electronic criteria, the aromaticity of [4n+2] π-electron porphyrinoids was evidenced as was the antiaromaticity for [4n] π-electron systems. -

Analytic Solution of the Schrцdinger Equation: Particle in A
Analytic solution of the Schrödinger equation: Particle in a box Notes on Quantum Mechanics http://quantum.bu.edu/notes/QuantumMechanics/ParticleInABox.pdf Last updated Tuesday, September 26, 2006 16:04:15-05:00 Copyright © 2004 Dan Dill ([email protected]) Department of Chemistry, Boston University, Boston MA 02215 One way to work with the curvature form of the Schrödinger equation, curvature of y at x ∂-kinetic energy at x μyat x, is try to guess what wavefunctions, y, satisfy it. For systems in which the kinetic energy changes with position in complicated ways, systematic implementation of this so-called analytic approach typically requires sophisticated mathematical machinery and so it not as easy to understand as the visual approach we will use. However, there is one example of the analytic approach that is very easy to understand, namely the case where a particle of mass m is confined in a one-dimensional region of width L; in this region it moves freely but it is not able to move outside this region. Such a system is called a particle in a box. It is one of the most important example quantum systems in chemistry, because it helps us develop intuition about the behavior on electrons confined in molecules. To use the analytical method, we begin by writing the Schrödinger equation more precisely as 2 m curvature of y at x =-ÅÅÅÅÅÅÅÅÅÅÅÅ μ kinetic energy at x μyat x. Ñ2 The reason the particle is able to move freely in the specified region, 0 § x § L (inside the "box"), is that its potential energy there is zero. -

Schrödinger Equation - Particle in a 1-D Box
Particle in a Box Outline - Review: Schrödinger Equation - Particle in a 1-D Box . Eigenenergies . Eigenstates . Probability densities 1 TRUE / FALSE The Schrodinger equation is given above. 1. The wavefunction Ψ can be complex, so we should remember to take the Real part of Ψ. 2. Time-harmonic solutions to Schrodinger equation are of the form: 3. Ψ(x,t) is a measurable quantity and represents the probability distribution of finding the particle. 2 Schrodinger: A Wave Equation for Electrons Schrodinger guessed that there was some wave-like quantity that could be related to energy and momentum … wavefunction 3 Schrodinger: A Wave Equation for Electrons (free-particle) (free-particle) ..The Free-Particle Schrodinger Wave Equation ! Erwin Schrödinger (1887–1961) 4 Image in the Public Domain Schrodinger Equation and Energy Conservation ... The Schrodinger Wave Equation ! Total E term K.E. term P.E . t e rm ... In physics notation and in 3-D this is how it looks: Electron Maximum height Potential and zero speed Energy Zero speed start Incoming Electron Fastest Battery 5 Time-Dependent Schrodinger Wave Equation To t a l E K.E. term P.E . t e rm PHYSICS term NOTATION Time-Independent Schrodinger Wave Equation 6 Particle in a Box e- 0.1 nm The particle the box is bound within certain regions of space. If bound, can the particle still be described as a wave ? YES … as a standing wave (wave that does not change its with time) 7 A point mass m constrained to move on an infinitely-thin, frictionless wire which is strung tightly between two impenetrable walls a distance L apart m 0 L WE WILL HAVE MULTIPLE SOLUTIONS FOR , SO WE INTRODUCE LABEL IS CONTINUOUS 8 WE WILL HAVE e- MULTIPLE SOLUTIONS FOR , SO WE INTRODUCE LABEL n L REWRITE AS: WHERE GENERAL SOLUTION: OR 9 USE BOUNDARY CONDITIONS TO DETERMINE COEFFICIENTS A and B e- since NORMALIZE THE INTEGRAL OF PROBABILITY TO 1 L 10 EIGENENERGIES for EIGENSTATES for PROBABILITY 1-D BOX 1-D BOX DENSITIES 11 Today’s Culture Moment Max Planck • Planck was a gifted musician. -
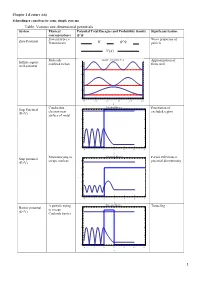
Table: Various One Dimensional Potentials System Physical Potential Total Energies and Probability Density Significant Feature Correspondence Free Particle I.E
Chapter 2 (Lecture 4-6) Schrodinger equation for some simple systems Table: Various one dimensional potentials System Physical Potential Total Energies and Probability density Significant feature correspondence Free particle i.e. Wave properties of Zero Potential Proton beam particle Molecule Infinite Potential Well Approximation of Infinite square confined to box finite well well potential 8 6 4 2 0 0.0 0.5 1.0 1.5 2.0 2.5 x Conduction Potential Barrier Penetration of Step Potential 4 electron near excluded region (E<V) surface of metal 3 2 1 0 4 2 0 2 4 6 8 x Neutron trying to Potential Barrier Partial reflection at Step potential escape nucleus 5 potential discontinuity (E>V) 4 3 2 1 0 4 2 0 2 4 6 8 x Α particle trying Potential Barrier Tunneling Barrier potential to escape 4 (E<V) Coulomb barrier 3 2 1 0 4 2 0 2 4 6 8 x 1 Electron Potential Barrier No reflection at Barrier potential 5 scattering from certain energies (E>V) negatively 4 ionized atom 3 2 1 0 4 2 0 2 4 6 8 x Neutron bound in Finite Potential Well Energy quantization Finite square well the nucleus potential 4 3 2 1 0 2 0 2 4 6 x Aromatic Degenerate quantum Particle in a ring compounds states contains atomic rings. Model the Quantization of energy Particle in a nucleus with a and degeneracy of spherical well potential which is or states zero inside the V=0 nuclear radius and infinite outside that radius. -

“Particle-In-A-Box” Problems in Quantum Mechanics
2-DIMENSIONAL “PARTICLE-IN-A-BOX” PROBLEMS IN QUANTUM MECHANICS Part I: Propagator & eigenfunctions by the method of images Nicholas Wheeler, Reed College Physics Department July 1997 Introduction. All strings make the same music, and support the same physics, because all strings have the same shape. The vibrational physics of a drumhead is, on the other hand, shape-dependent—whence Mark Kac’famous question: “Can one hear the shape of a drum?”1 Relatedly, all instances of the quantum mechanical “particle-in-a-box” problem are, in the one-dimensional case, scale- equivalent to one another, but higher-dimensional instances of the same problem are (in general) inequivalent. Though the one-dimensional box-problem yields quite readily to exact closed-form analysis—the simplest (but only the simplest!) aspects of which can be found in every quantum text—the higher-dimensional problem (N ≥ 2) is in most of its aspects analytically intractable except in certain special cases. In previous work2 I have identified a class of cases that yield to analysis by what might be called the “quantum mechanical method of images.” I undertake the present review of the essentials of that work partly to make it more readily available to students of quantum mechanics, but mainly to be responsive to an expressed need of my colleague Oz Bonfim, who speculates that some of my results may be relevent to his own work in connection with the so-called “Bohm interpretation of quantum mechanics.”3 I have also an ulterior motivation, 1 Amer. Math. Monthly 73, 1 (1966). This classic paper is reprinted in Mark Kac: Selected Papers on Probability, Number Theory & Statistical Physics () 2 feynman formalism for polygonal domains (–); circular boxes & rigid wavepackets (–). -

Course of Study
Introduction to Quantum Chemistry and Spectroscopy CY41009; Autumn Semester 2016-2017 Course of Study 1. Birth of Quantum Mechanics Failures of Classical Mechanics in Black Body Radition, Photoelectric Effects, Heat capacity of Solids, and Atomic Spectra; Quantum Mechanics - the Saviour; Birth of Quantum Chemistry. 2. Principles and Postulates of Quantum Mechanics State Functions; Operators; Eigenfunctions; Expectation Values; Time Evolution of Expectation Values; Ehrenfest Theorem; Hermitian Property; Schmidt Orthogonalization; Dirac Notation; Dirac Delta Function; Commutation of Operators; Heisenberg's Uncertainty Principle; Parity Operator. 3. Exactly Solvable Models • Translational Motions Particle in a 1D box; Bohr's Correspondence Principle; Free Particle; Particle in a 3D box; Degeneracies; Particle in a Rectangular Well; Tunneling Through Barrier; Scanning Tunneling Microscopy. • Vibrational Motions Harmonic Oscillators; Creation-Annihilation Operators; Hermite Polynomials; Vibrational Spectroscopy • Angular Motions Angular Momentum Operators; Ladder Operators; Spherical Harmonics. • Rotational Motions Particle in a ring; Particle on a sphere; Rigid Rotor; • Hydrogen Atom Solution of H-atom; Bound-state H-atom Wave Functions; Radial Distribution Functions; H-like Orbitals; Zeeman Effect; H-atom with Electron Spin; Spin-Orbit Interaction; Atomic Spectra with Spin-Orbit Interac- tion in Magnetic Field. 4. Approximate Methods Variational Theorem; He atom with Variational Method; Perturbation Theory; 1st and 2nd Order Perturbation Correction -

Quantum Mechanics (Surprising !!!) the Analysis of Electronic Flow)
2/6/2019 INE: Revision INTRODUCTION TO NANOELECTRONICS Week-6, Lecture-2 Sneh Saurabh 6th February, 2019 Introduction to Nanoelectronics: S. Saurabh Overview 2 A free particle: Significance in Solid State Physics Seminal concept in solid state physics Impact on Analysis . In crystalline solids electrons behave as if . Reduces the complicated problem of they are in vacuum, but with an effective electron waves in a crystalline solid to that mass different from their natural mass of waves in vacuum (Dramatically eases Quantum Mechanics (Surprising !!!) the analysis of electronic flow) . Energy-momentum relation 푝 . Valid for several materials such as Copper (metal) and Silicon (semiconductor) in wide 퐸 푝 = 퐸 + ∗ 2푚 range of energies . Energy-wavenumber (퐸 − 푘) relation (using . Parabolic 퐸 − 푘 푟푒푙푎푡푖표푛푠ℎ푖푝 푝 = ℏ푘) A Free particle ℏퟐ풌ퟐ (퐷푖푠푝푒푟푠푖표푛 푟푒푙푎푡푖표푛푠ℎ푖푝) is not valid for 퐸 푘 = 퐸 + some materials such as graphene 2푚∗ Introduction to Nanoelectronics: S. Saurabh Quantum Mechanics 3 Introduction to Nanoelectronics: S. Saurabh Quantum Mechanics 4 1 2/6/2019 A free particle + particle in a box ! Wave function of an electron in a confined nanoelectronic device can be treated as combined effect of (a free particle + a particle in a box) Quantum Mechanics Bulk Quantum Quantum Quantum (3D) Well (2D) Wire (1D) Dots (0D) 3-D Schrödinger Equation Introduction to Nanoelectronics: S. Saurabh Quantum Mechanics 5 Introduction to Nanoelectronics: S. Saurabh Quantum Mechanics 6 Schrödinger Equation: 3-D Schrödinger Equation: 3-D Separable solution (1) Three-dimensional time-independent Schrödinger equation: . Applying quantum mechanics to nanostructures (which are naturally 3-D objects) requires 퐻휓(푥, 푦, 푧)= 퐸휓(푥, 푦, 푧) extending Schrödinger Equation to 3-D where: ℏ 휕 휕 휕 . -

Quantum Mechanics Recap
Chapter 2 Quantum Mechanics in a Nutshell 2.1 Introduction 2.2 Photons Time: end of the 19th century. Maxwell’s equations have established Faraday’s hunch that light is an electromagnetic wave. However, by early 20th century, experimental evidence mounted pointing towards the fact that light is carried by ‘particles’ that pack a definite momentum and energy. Here is the crux of the problem: consider the double-slit experiment. Monochromatic light of wavelength λ passing through two slits separated by a distance d λ forms a di↵raction pattern on a photographic plate. If one ⇠ tunes down the intensity of light in a double-slit experiment, one does not get a ‘dimmer’ interference pattern, but discrete strikes on the photographic plate and illumination at specific points. That means light is composed of ‘particles’ whose energy and momentum are concentrated in one point which leads to discrete hits. But their wavelength extends over space, which leads to di↵raction patterns. Planck postulated that light is composed of discrete lumps of momemtum p = ~k and energy E = ~!. Here k =(2⇡/λ)ˆn , ˆn the direction of propagation, ~ is Planck’s constant, and ! = c k with c the speed of light. Planck’s hypothesis explained spectral | | features of the blackbody radiation. It was used by Einstein to explain the photoelectric e↵ect. Einstein was developing the theory of relativity around the same time. In this theory, the momentum of a particle of mass m and velocity v is p = mv/ 1 (v/c)2, − where c is the speed of light. Thus if a particle has m = 0, the only way itp can pack a momentum is if its velocity is v = c.