Identifying Compact Moving Groups Based on Stellar Kinematics Data A
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

University of Groningen Kinematics and Stellar Populations of Dwarf
University of Groningen Kinematics and stellar populations of dwarf elliptical galaxies Mentz, Jacobus Johannes IMPORTANT NOTE: You are advised to consult the publisher's version (publisher's PDF) if you wish to cite from it. Please check the document version below. Document Version Publisher's PDF, also known as Version of record Publication date: 2018 Link to publication in University of Groningen/UMCG research database Citation for published version (APA): Mentz, J. J. (2018). Kinematics and stellar populations of dwarf elliptical galaxies. Rijksuniversiteit Groningen. Copyright Other than for strictly personal use, it is not permitted to download or to forward/distribute the text or part of it without the consent of the author(s) and/or copyright holder(s), unless the work is under an open content license (like Creative Commons). The publication may also be distributed here under the terms of Article 25fa of the Dutch Copyright Act, indicated by the “Taverne” license. More information can be found on the University of Groningen website: https://www.rug.nl/library/open-access/self-archiving-pure/taverne- amendment. Take-down policy If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. Downloaded from the University of Groningen/UMCG research database (Pure): http://www.rug.nl/research/portal. For technical reasons the number of authors shown on this cover page is limited to 10 maximum. Download date: 09-10-2021 Kinematics and stellar populations of dwarf elliptical galaxies Proefschrift ter verkrijging van het doctoraat aan de Rijksuniversiteit Groningen op gezag van de rector magnificus prof. -

A Radial Velocity Survey of the Carina Nebula's O-Type Stars
A radial velocity survey of the Carina Nebula's O-type stars Item Type Article Authors Kiminki, Megan M; Smith, Nathan Citation Megan M Kiminki, Nathan Smith; A radial velocity survey of the Carina Nebula's O-type stars, Monthly Notices of the Royal Astronomical Society, Volume 477, Issue 2, 21 June 2018, Pages 2068–2086, https://doi.org/10.1093/mnras/sty748 DOI 10.1093/mnras/sty748 Publisher OXFORD UNIV PRESS Journal MONTHLY NOTICES OF THE ROYAL ASTRONOMICAL SOCIETY Rights © 2018 The Author(s) Published by Oxford University Press on behalf of the Royal Astronomical Society. Download date 30/09/2021 21:29:15 Item License http://rightsstatements.org/vocab/InC/1.0/ Version Final published version Link to Item http://hdl.handle.net/10150/628380 MNRAS 477, 2068–2086 (2018) doi:10.1093/mnras/sty748 Advance Access publication 2018 March 21 A radial velocity survey of the Carina Nebula’s O-type stars Megan M. Kiminki‹ and Nathan Smith Steward Observatory, University of Arizona, 933 N. Cherry Avenue, Tucson, AZ 85721, USA Accepted 2018 March 14. Received 2018 March 11; in original form 2017 June 17 ABSTRACT We have obtained multi-epoch observations of 31 O-type stars in the Carina Nebula using the CHIRON spectrograph on the CTIO/SMARTS 1.5-m telescope. We measure their radial velocities to 1–2 km s−1 precision and present new or updated orbital solutions for the binary systems HD 92607, HD 93576, HDE 303312, and HDE 305536. We also compile radial velocities from the literature for 32 additional O-type and evolved massive stars in the region. -

Stellar Dynamics and Stellar Phenomena Near a Massive Black Hole
Stellar Dynamics and Stellar Phenomena Near A Massive Black Hole Tal Alexander Department of Particle Physics and Astrophysics, Weizmann Institute of Science, 234 Herzl St, Rehovot, Israel 76100; email: [email protected] | Author's original version. To appear in Annual Review of Astronomy and Astrophysics. See final published version in ARA&A website: www.annualreviews.org/doi/10.1146/annurev-astro-091916-055306 Annu. Rev. Astron. Astrophys. 2017. Keywords 55:1{41 massive black holes, stellar kinematics, stellar dynamics, Galactic This article's doi: Center 10.1146/((please add article doi)) Copyright c 2017 by Annual Reviews. Abstract All rights reserved Most galactic nuclei harbor a massive black hole (MBH), whose birth and evolution are closely linked to those of its host galaxy. The unique conditions near the MBH: high velocity and density in the steep po- tential of a massive singular relativistic object, lead to unusual modes of stellar birth, evolution, dynamics and death. A complex network of dynamical mechanisms, operating on multiple timescales, deflect stars arXiv:1701.04762v1 [astro-ph.GA] 17 Jan 2017 to orbits that intercept the MBH. Such close encounters lead to ener- getic interactions with observable signatures and consequences for the evolution of the MBH and its stellar environment. Galactic nuclei are astrophysical laboratories that test and challenge our understanding of MBH formation, strong gravity, stellar dynamics, and stellar physics. I review from a theoretical perspective the wide range of stellar phe- nomena that occur near MBHs, focusing on the role of stellar dynamics near an isolated MBH in a relaxed stellar cusp. -

Probabilistic Fundamental Stellar Parameters
Solving some r-process issues in chemical evolution Ralph Schönrich (Oxford) Paul McMillan, Laurent Eyer, Walter Dehnen James Binney, Michael Aumer, Luca Casagrande Martin Asplund, David Weinberg Hokotezaka et al. (2018) Chemical evolution gas inflow/onflow IGM stars Chemical evolution gas Fe-rich inflow/onflow SNIa SNII+Ib,c IGM a-rich progenitors stars Chemical evolution gas Fe-rich inflow/onflow SNIa SNII+Ib,c IGM a-rich r-process progenitors outflow NM stars Hokotezaka et al. (2018) Some simple thoughts Assume constant loss fraction from yields What about the thick disc ridge? Neutron star mergers → r process later Doing a simple model Doing a simple model Chemical evolution gas Fe-rich inflow/onflow SNIa SNII+Ib,c IGM a-rich r-process progenitors outflow NM stars Trying to escape the usual links Hot air does not only make you fly, it can delay your evolution Short-lived isotopes in the early solar system Wasserburg et al. (2006) Chemical evolution gas condensation warm cool evaporation Fe-rich inflow/onflow direct enrichment SNIa SNII+Ib,c IGM a-rich r-process progenitors outflow NM stars Introducing the hot gas phase Introducing the hot gas phase Some simple thoughts Assume constant loss fraction from yields What about the thick disc ridge? Neutron star mergers → r process later Some simple thoughts Assume constant loss fraction from yields What about the thick disc ridge? Neutron star mergers → r process later Using the different factor Using the different factor Summary The hot vs. cold ISM is central for the evolution of „early“ -

Detection and Characterization of Hot Subdwarf Companions of Massive Stars Luqian Wang
Georgia State University ScholarWorks @ Georgia State University Physics and Astronomy Dissertations Department of Physics and Astronomy 8-13-2019 Detection And Characterization Of Hot Subdwarf Companions Of Massive Stars Luqian Wang Follow this and additional works at: https://scholarworks.gsu.edu/phy_astr_diss Recommended Citation Wang, Luqian, "Detection And Characterization Of Hot Subdwarf Companions Of Massive Stars." Dissertation, Georgia State University, 2019. https://scholarworks.gsu.edu/phy_astr_diss/119 This Dissertation is brought to you for free and open access by the Department of Physics and Astronomy at ScholarWorks @ Georgia State University. It has been accepted for inclusion in Physics and Astronomy Dissertations by an authorized administrator of ScholarWorks @ Georgia State University. For more information, please contact [email protected]. DETECTION AND CHARACTERIZATION OF HOT SUBDWARF COMPANIONS OF MASSIVE STARS by LUQIAN WANG Under the Direction of Douglas R. Gies, PhD ABSTRACT Massive stars are born in close binaries, and in the course of their evolution, the initially more massive star will grow and begin to transfer mass and angular momentum to the gainer star. The mass donor star will be stripped of its outer envelope, and it will end up as a faint, hot subdwarf star. Here I present a search for the subdwarf stars in Be binary systems using the International Ultraviolet Explorer. Through spectroscopic analysis, I detected the subdwarf star in HR 2142 and 60 Cyg. Further analysis led to the discovery of an additional 12 Be and subdwarf candidate systems. I also investigated the EL CVn binary system, which is the prototype of class of eclipsing binaries that consist of an A- or F-type main sequence star and a low mass subdwarf. -

Book of Abstracts
KIAA / DoA 2019 Postdoc Science Days Book of Abstracts December 10th and 11th 2019 in the KIAA Auditorium Schedule Time Speaker Title Page k Tuesday December 10th 2019: 9:30 - 9:35 Gregory Herczeg Introduction Galaxy Formation and Evolution 9:35 - 9:55 Tomonari Michiyama (道山知成) Sub-mm observations of nearby merging galaxies 3 9:55 - 10:15 Bumhyun Lee (이범현) Deep Impact: molecular gas properties under strong ram pressure 3 10:15 - 10:35 Kexin Guo (郭可欣) The Roles of AGNs and Dynamical Process in Star Formation Quenching in Nearby 4 Disk Galaxies 10:35 - 10:55 Sonali Sachdeva Correlation of structure and stellar properties of galaxies 4 10:55 - 11:15 Min Du (杜敏) Intrinsic structures of disk galaxies identified in kinematics 5 Tea & Coffee Break Pulsars and Radio Sources 11:35 - 11:55 Xuhao Wu (武旭浩) How Can The Pulsar’s Maximum Mass Reach ∼3 M⊙ 5 11:55 - 12:15 Nicolas Caballero Pulsar-based timescales 5 12:15 - 12:35 Wei Hua Wang (汪卫华) The unique post-glitch behavior of the Crab pulsar as a possible signature of 6 superfluid PBF Lunch ISM, Star-Formation, and Supernovae 13:40 - 14:00 Toky Randriamampandry CALIFA bar pattern speed: toward a bar scaling relation 6 14:00 - 14:20 Moran Xia (夏默然) The Origin of The Stellar Mass-Stellar Metallicity Relation In the Milky Way 7 Satellites and Beyond 14:20 - 14:40 Juan Molina A spatially-resolved view of the gas kinematics in two star-forming galaxies at z~1.47 7 seen with ALMA and VLT-SINFONI 14:40 - 15:00 John Graham The Metallicity Distribution of Type II SNe Hosts 8 Tea & Coffee Break Active Galactic -

The Galaxy in Context: Structural, Kinematic & Integrated Properties
The Galaxy in Context: Structural, Kinematic & Integrated Properties Joss Bland-Hawthorn1, Ortwin Gerhard2 1Sydney Institute for Astronomy, School of Physics A28, University of Sydney, NSW 2006, Australia; email: [email protected] 2Max Planck Institute for extraterrestrial Physics, PO Box 1312, Giessenbachstr., 85741 Garching, Germany; email: [email protected] Annu. Rev. Astron. Astrophys. 2016. Keywords 54:529{596 Galaxy: Structural Components, Stellar Kinematics, Stellar This article's doi: 10.1146/annurev-astro-081915-023441 Populations, Dynamics, Evolution; Local Group; Cosmology Copyright c 2016 by Annual Reviews. Abstract All rights reserved Our Galaxy, the Milky Way, is a benchmark for understanding disk galaxies. It is the only galaxy whose formation history can be stud- ied using the full distribution of stars from faint dwarfs to supergiants. The oldest components provide us with unique insight into how galaxies form and evolve over billions of years. The Galaxy is a luminous (L?) barred spiral with a central box/peanut bulge, a dominant disk, and a diffuse stellar halo. Based on global properties, it falls in the sparsely populated \green valley" region of the galaxy colour-magnitude dia- arXiv:1602.07702v2 [astro-ph.GA] 5 Jan 2017 gram. Here we review the key integrated, structural and kinematic pa- rameters of the Galaxy, and point to uncertainties as well as directions for future progress. Galactic studies will continue to play a fundamen- tal role far into the future because there are measurements that can only be made in the near field and much of contemporary astrophysics depends on such observations. 529 Redshift (z) 20 10 5 2 1 0 1012 1011 ) ¯ 1010 M ( 9 r i 10 v 8 M 10 107 100 101 102 ) c p 1 k 10 ( r i v r 100 10-1 0.3 1 3 10 Time (Gyr) Figure 1 Left: The estimated growth of the Galaxy's virial mass (Mvir) and radius (rvir) from z = 20 to the present day, z = 0. -
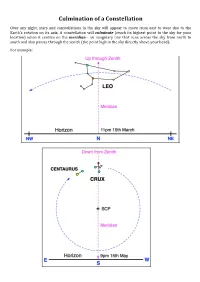
Culmination of a Constellation
Culmination of a Constellation Over any night, stars and constellations in the sky will appear to move from east to west due to the Earth’s rotation on its axis. A constellation will culminate (reach its highest point in the sky for your location) when it centres on the meridian - an imaginary line that runs across the sky from north to south and also passes through the zenith (the point high in the sky directly above your head). For example: When to Observe Constellations The taBle shows the approximate time (AEST) constellations will culminate around the middle (15th day) of each month. Constellations will culminate 2 hours earlier for each successive month. Note: add an hour to the given time when daylight saving time is in effect. The time “12” is midnight. Sunrise/sunset times are rounded off to the nearest half an hour. Sun- Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec Rise 5am 5:30 6am 6am 7am 7am 7am 6:30 6am 5am 4:30 4:30 Set 7pm 6:30 6pm 5:30 5pm 5pm 5pm 5:30 6pm 6pm 6:30 7pm And 5am 3am 1am 11pm 9pm Aqr 5am 3am 1am 11pm 9pm Aql 4am 2am 12 10pm 8pm Ara 4am 2am 12 10pm 8pm Ari 5am 3am 1am 11pm 9pm Aur 10pm 8pm 4am 2am 12 Boo 3am 1am 11pm 9pm 7pm Cnc 1am 11pm 9pm 7pm 3am CVn 3am 1am 11pm 9pm 7pm CMa 11pm 9pm 7pm 3am 1am Cap 5am 3am 1am 11pm 9pm 7pm Car 2am 12 10pm 8pm 6pm Cen 4am 2am 12 10pm 8pm 6pm Cet 4am 2am 12 10pm 8pm Cha 3am 1am 11pm 9pm 7pm Col 10pm 8pm 4am 2am 12 Com 3am 1am 11pm 9pm 7pm CrA 3am 1am 11pm 9pm 7pm CrB 4am 2am 12 10pm 8pm Crv 3am 1am 11pm 9pm 7pm Cru 3am 1am 11pm 9pm 7pm Cyg 5am 3am 1am 11pm 9pm 7pm Del -

Mass Models of NGC 6624 Without an Intermediate-Mass Black Hole
MNRAS 473, 4832–4839 (2018) Preprint 30 November 2017 Compiled using MNRAS LATEX style file v3.0 Mass models of NGC 6624 without an intermediate-mass black hole Mark Gieles1?, Eduardo Balbinot1, Rashid I.S.M. Yaaqib1,Vincent Hénault-Brunet2, Alice Zocchi3;4, Miklos Peuten1, Peter G. Jonker2;5 1 Department of Physics, University of Surrey, Guildford, GU2 7XH, UK 2 Department of Astrophysics/IMAPP, Radboud University, PO Box 9010, 6500 GL Nijmegen, The Netherlands 3 Dipartimento di Fisica e Astronomia, Università degli Studi di Bologna, viale Berti Pichat 6/2, I40127, Bologna, Italy 4 INAF - Osservatorio Astronomico di Bologna, Via Ranzani 1, I40127 Bologna, Italy 5 SRON, Netherlands Institute for Space Research, Sorbonnelaan 2, NL-3584 CA Utrecht, The Netherlands Accepted 2017 October 11. Received 2017 11; in original form 2017 August 10 ABSTRACT An intermediate-mass black hole (IMBH) was recently reported to reside in the centre of the Galactic globular cluster (GC) NGC 6624, based on timing observations of a millisecond pul- sar (MSP) located near the cluster centre in projection. We present dynamical models with multiple mass components of NGC 6624 – without an IMBH – which successfully describe the surface brightness profile and proper motion kinematics from the Hubble Space Tele- scope (HST) and the stellar-mass function at different distances from the cluster centre. The maximum line-of-sight acceleration at the position of the MSP accommodates the inferred acceleration of the MSP, as derived from its first period derivative. With discrete realizations of the models we show that the higher-order period derivatives – which were previously used to derive the IMBH mass – are due to passing stars and stellar remnants, as previously shown analytically in literature. -

Subgiants As Probes of Galactic Chemical Evolution
Astronomy & Astrophysics manuscript no. Thoren September 9, 2018 (DOI: will be inserted by hand later) Subgiants as probes of galactic chemical evolution ⋆, ⋆⋆, ⋆⋆⋆ Patrik Thor´en, Bengt Edvardsson and Bengt Gustafsson Department of Astronomy and Space Physics, Uppsala Astronomical Observatory, Box 515, S-751 20 Uppsala, Sweden Received 12 March 2004 / Accepted 28 May 2004 Abstract. Chemical abundances for 23 candidate subgiant stars have been derived with the aim at exploring their usefulness for studies of galactic chemical evolution. High-resolution spectra from ESO CAT-CES and NOT- SOFIN covered 16 different spectral regions in the visible part of the spectrum. Some 200 different atomic and molecular spectral lines have been used for abundance analysis of ∼ 30 elemental species. The wings of strong, pressure-broadened metal lines were used for determination of stellar surface gravities, which have been compared with gravities derived from Hipparcos parallaxes and isochronic masses. Stellar space velocities have been derived from Hipparcos and Simbad data, and ages and masses were derived with recent isochrones. Only 12 of the stars turned out to be subgiants, i.e. on the “horizontal” part of the evolutionary track between the dwarf- and the giant stages. The abundances derived for the subgiants correspond closely to those of dwarf stars. With the possible exceptions of lithium and carbon we find that subgiant stars show no “chemical” traces of post-main-sequence evolution and that they are therefore very useful targets for studies of galactic chemical evolution. Key words. stars:abundances – stars:evolution – galaxy:abundances – galaxy:evolution 1. Introduction The volume is limited by the low luminosities of the dwarfs used in the surveys, and by the limited view in cer- Abundance patterns in stellar populations have proven to tain directions through the galactic disk. -

Merging Black Holes in the Low-Mass and High-Mass Gaps from 2 + 2
The Astrophysical Journal Letters, 895:L15 (8pp), 2020 May 20 https://doi.org/10.3847/2041-8213/ab9093 © 2020. The American Astronomical Society. All rights reserved. Merging Black Holes in the Low-mass and High-mass Gaps from 2+2 Quadruple Systems Giacomo Fragione1,2 , Abraham Loeb3 , and Frederic A. Rasio1,2 1 Department of Physics & Astronomy, Northwestern University, Evanston, IL 60208, USA 2 Center for Interdisciplinary Exploration & Research in Astrophysics (CIERA), USA 3 Astronomy Department, Harvard University, 60 Garden Street, Cambridge, MA 02138, USA Received 2020 February 24; revised 2020 May 4; accepted 2020 May 6; published 2020 May 21 Abstract The origin of the black hole (BH) binary mergers observed by LIGO-Virgo is still uncertain, as are the boundaries of the stellar BH mass function. Stellar evolution models predict a dearth of BHs both at masses 50 M and 5 M , thus leaving low- and high-mass gaps in the BH mass function. A natural way to form BHs of these masses is through mergers of neutron stars (NSs; for the low-mass gap) or lower-mass BHs (for the high-mass gap); the low- or high-mass-gap BH produced as a merger product can then be detected by LIGO-Virgo if it merges again with a new companion. We show that the evolution of a 2+2 quadruple system can naturally lead to BH mergers with component masses in the low- or high-mass gaps. In our scenario, the BH in the mass gap originates from the merger of two NSs, or two BHs, in one of the two binaries and the merger product is imparted a recoil kick (from anisotropic gravitational wave emission), which triggers its interaction with the other binary component of the quadruple system. -

Optical Studies of X-Ray Sources in the Old Open Cluster M 67
Optical studies of X-ray sources in the old open cluster M 67 Figures 1.1 and 8.1, the images in the chapter headings and the images at the end are created from the Digitized Sky Survey c 2001 Maureen van den Berg Alle rechten voorbehouden. Niets in deze uitgave mag worden verveelvoudigd, opgesla- gen in een geautomatiseerd gegevensbestand, of openbaar gemaakt, in enige vorm, zonder schriftelijke toestemming van de auteur ISBN 90-393-2679-7 Optical studies of X-ray sources in the old open cluster M 67 Optische studies van rontgenbronnen¨ in de oude open sterrenhoop M 67 (met een samenvatting in het Nederlands) Proefschrift ter verkrijging van de graad van doctor aan de Universiteit Utrecht op gezag van de Rector Magnificus prof. dr H.O. Voorma ingevolge het besluit van het College voor Promoties, in het openbaar te verdedigen op woensdag 21 maart 2001 des ochtends te 10.30 uur door Maureen Constance van den Berg geboren op 6 april 1972 te Maastricht PROMOTOR prof. dr Frank Verbunt Dit proefschrift werd mede mogelijk gemaakt met financiele¨ steun van de Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NWO). Contents 1 Introduction 1 1.1 Blue stragglers, yellow stragglers and sub-subgiants 1 1.2 X-ray observations of old open clusters 3 1.3 Summary: peculiar X-ray sources in M 67, NGC 752 and NGC 6940 5 2 Optical spectroscopy of X-ray sources in the old open cluster M67 9 2.1 Introduction 10 2.2 Observations and data reduction 12 2.2.1 Low-resolution spectra 14 2.2.2 High-resolution spectra 14 2.3 Data analysis 15 2.3.1 Determination of Ca II H&K emission fluxes 15 2.3.2 Determination of projected rotational velocities 17 2.4 Results 19 2.4.1 Comparison with RS CVn binaries 19 2.4.2 Activity indicators 21 2.4.3 Individual systems 22 2.5 Discussion and conclusions 26 3 Photometric variability in the old open cluster M 67 I.