Cryptography Cryptography Communication Security
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Secret Wri0ng Steganography
Secret wring LIVITCSWPIYVEWHEVSRIQMXLEYVEOIEWHRXEXIP FEMVEWHKVSTYLXZIXLIKIIXPIJVSZEYPERRGERI MWQLMGLMXQERIWGPSRIHMXQEREKIETXMJTPRGEV EKEITREWHEXXLEXXMZITWAWSQWXSWEXTVEPMRXR SJGSTVRIEYVIEXCVMUIMWERGMIWXMJMGCSMWXSJ OMIQXLIVIQIVIXQSVSTWHKPEGARCSXRWIEVSWII BXVIZMXFSJXLIKEGAEWHEPSWYSWIWIEVXLISXLI VXLIRGEPIRQIVIIBGIIHMWYPFLEVHEWHYPSRRFQ MXLEPPXLIECCIEVEWGISJKTVWMRLIHYSPHXLIQI MYLXSJXLIMWRIGXQEROIVFVIZEVAEKPIEWHXEAM WYEPPXLMWYRMWXSGSWRMHIVEXMSWMGSTPHLEVHP FKPEZINTCMXIVJSVLMRSCMWMSWVIRCIGXMWYMX CSCI 470: Web Science • Keith Vertanen • Copyright © 2014 Overview • Secret wri+ng – Steganography – Cryptography • Keys, plaintext, ciphertext • Codes vs. Ciphers • Transposi+on ciphers • Subs+tu+on ciphers 2 Steganography vs. Cryptography • Steganography – "concealed wri+ng" – Hide messages to keep secret – Does not aract aen+on (iF not Found). • Cryptography – "hidden wring" – Scramble messages so unintelligible – Screams: "Please try and decode me!" • But not mutually exclusive: – e.g. Scrambled message in "invisible" ink 3 Physical hiding • Ancient Chinese – Write message on very thin silk sheet – Rolled up, covered in wax, and ingested by messenger • 480 BC – His+aeus wants Aristagoras oF Miletus to revolt against the Persian King • Shaves head oF messenger, taoos message on scalp • Wait For hair to grow back • Sends messenger to Aristagoras 4 Physical hiding • 480 BC – Demaratus, Greek ex-pat living in Persia – No+ces build up For aack on Greece – Sent secret messages: • Scraped wax oF tablet • Wrote on wood • Covered up with wax – Persian ships -

Enigma Cryptanalysis - Beginnings
Enigma Cryptanalysis - Beginnings Gaurish Korpal∗ [email protected] July 15, 2015 Abstract Any message may be hidden in two basic ways. The methods of steganography conceal the very existence of the message, for example invisible inks and microdots. The methods of cryptography, on the other hand, do not conceal the presence of a secret message but render it unintelligible as ciphertext, to outsiders by various transformations of the plaintext. Breaking ciphers require ingenuity, creativity and a little math. In this article our focus will be on breaking Enigma ciphers. The skill involved in breaking ciphers is called cryptanalysis. Keywords. Enigma, cryptanalysis, cypher, Caesar, Vigen`ere,Rejewski, Zygalski, Bomba, Bombe 1 Cipher not Code A code is a mapping from some meaningful unit (word, sentence, phrase) into something else (usually a shorter group of symbols). A code requires a codebook, it is simply a list of these mappings. For example we could make up a code where the word Apple is written as 67, historical example of this is \Zimmermann Telegram Code" for more details refer [7]. Ciphers do not involve meaning. Instead they are mechanical operations (known as algorithms) which are performed on the individual or small chunks of letters. A code is stored as a mapping in a codebook, while ciphers transform individual symbols according to an algorithm. It was definitively stated in 1883 by the Dutch linguist Auguste Kerckhoffs von Nieuwenhof in his book La Cryptographie militaire: Kerckhoffs' Principle: The security of a cryptosystem must not depend on keeping secret the crypto-algorithm. The security depends only on keeping secret the key. -

Q.1 What Is Cryptography? Ans. Cryptographic
WWW.UPTUNOTES.COM Q.1 What is cryptography? Ans. Cryptographic systems are generally classified along 3 independent dimensions: Type of operations used for transforming plain text to cipher text All the encryption algorithms are based on two general principles: substitution, in which each element in the plaintext is mapped into another element, and transposition, in which elements in the plaintext are rearranged. The number of keys used are: 1. If the sender and receiver uses same key then it is said to be symmetric key (or) single key (or) conventional encryption. 2. If the sender and receiver use different keys then it is said to be public key encryption. Q.2 Explain the Cryptanalysis? Ans. The process of attempting to discover X or K or both is known as cryptanalysis. The strategy used by the cryptanalysis depends on the nature of the encryption scheme and the information available to the cryptanalyst. Q.3 Write down the various types of cryptanalytic attacks? Ans. There are various types of cryptanalytic attacks based on the amount of information known to the cryptanalyst. 1. Cipher Text Only – A copy of cipher text alone is known to the cryptanalyst. 2. Known Plaintext – The cryptanalyst has a copy of the cipher text and the corresponding plaintext. 3. Chosen Plaintext – The cryptanalysts gains temporary access to the encryption machine. They cannot open it to find the key, however; they can encrypt a large number of suitably chosen plaintexts and try to use the resulting cipher texts to deduce the key. 4. Chosen Cipher Text – The cryptanalyst obtains temporary access to the decryption machine, uses it to decrypt several string of symbols, and tries to use the results to deduce the key. -

Download Magzter App from Andriod Apple Store Rakesh U Kishore P
INTERVIEW-Samir INTERVIEW:VijayMinocha REGULATIONS COGOPORT TERMINALS:Dowe JShah:“Pro-actively "IoTwillDriveGreater EaseofTrade TheDigitalEraof NeedAutomated ComplytoTFAREGIME” Efficiency” throughTFA MovingCargo Terminals? South Asia’s premier maritime business magazine `100 AUGUST 2017 WWW.MARITIMEGATEWAY.COM RNI NO: TELENG/2009/30633 POSTAL REGISTRATION NO: LII/RNP/HD/1137/2016-18 TheCruiseandTheGoldenEgg DATE OF PUBLICATION: 26/07/2017 DATE OF POSTING: 28/07/2017 CYBERCYBER AATTTTACKSACKS WILLWILL HURTHURT YYOUOU BEBE PREPPREPAREDARED TOTO DEALDEAL WITHWITH ESCALAESCALATINGTING OFFENSIVESOFFENSIVES 02 MARITIME GATEWAY / AUGUST 2017 Automate, connect and control with Cavotec’s inspired engineering. Cavotec is a global engineering group that manufactures power transmission, distribution and control technologies that form the link between fixed and mobile equipment in the Ports & Maritime, Airports, Mining & Tunnelling and General Industry sectors. Cavotec India Pvt Ltd Telephone: +91 20 6725 5000 Fax: +91 20 6725 5099 [email protected] Inspired Engineering www.cavotec.com FROM THE EDITOR Watch Out! The e-pirates are at sea here do you think the formal maritime cyber security cell, hackers are going to play vessel operators should protect their their favourite sport next? three keys navigational systems- GPS, WYes, at sea. The shipping AIS and ECDIS. industry that transports 90 per cent Of late, many vessels have left Somali Reliance on of the world’s trade has made itself pirates smarting by turning off the increasingly susceptible to cyber threats. AIS or faking a location to divert the automation cannot With shipping companies making a lot attention of the mischief makers. compromise cyber of data accessible to their customers However, it is only a matter of time through their mobile applications, the when these faceless pirates can security. -

Crypyto Documentation Release 0.2.0
crypyto Documentation Release 0.2.0 Yan Orestes Aug 22, 2018 API Documentation 1 Getting Started 3 1.1 Dependencies...............................................3 1.2 Installing.................................................3 2 Ciphers 5 2.1 Polybius Square.............................................5 2.2 Atbash..................................................6 2.3 Caesar Cipher..............................................7 2.4 ROT13..................................................8 2.5 Affine Cipher...............................................9 2.6 Rail Fence Cipher............................................9 2.7 Keyword Cipher............................................. 10 2.8 Vigenère Cipher............................................. 11 2.9 Beaufort Cipher............................................. 12 2.10 Gronsfeld Cipher............................................. 13 3 Substitution Alphabets 15 3.1 Morse Code............................................... 15 3.2 Binary Translation............................................ 16 3.3 Pigpen Cipher.............................................. 16 3.4 Templar Cipher.............................................. 18 3.5 Betamaze Alphabet............................................ 19 Python Module Index 21 i ii crypyto Documentation, Release 0.2.0 crypyto is a Python package that provides a set of cryptographic tools with simple use to your applications. API Documentation 1 crypyto Documentation, Release 0.2.0 2 API Documentation CHAPTER 1 Getting Started These instructions -

Rail Fence Cipher Columnar Transposition
Mathematics 124 (Winter 2009) Transposition Ciphers A transposition cipher is one in which plaintext symbols are rearranged (i.e., transposed or permuted) to produce ciphertext. The method of transposition may be either mathematical or typographical in nature. Rail Fence Cipher Example: We encipher NOTHING IS AS IT SEEMS by first writing it on two lines in a zig-zag pattern (or rail fence). The ciphertext is produced by transcribing the first row followed by the second row. NTIGSSTEM OHNIAISES Ciphertext: NTIGS STEMO HNIAI SES. To decrypt, we write half the letters on one line, half on the second. (Note that if there are an odd number of letters, we include the “middle” letter on the top line.) Example: Decipher MKHSE LWYAE ATSOL. Solution: Since there are 15 letters, we write 8 on the top line and 7 on the bottom line so that MKHSELWY AEATSOL Plaintext: MAKE HASTE SLOWLY. Columnar Transposition The number of columns is the key information. To encipher: Plaintext is written horizontally in k columns, and is then transcribed vertically column- by-column, To decipher: Suppose that the length of the ciphertext is n and the key is k. Then the letters will fill n DIV k full rows, and there will be one partial row at the end with n MOD k letters. Transcribing row-by-row will then yield the plaintext. Example: Encrypt NOTHING IN THE WORLD IS MORE DANGEROUS THAN SINCERE IGNORANCE AND CONSCIENTIOUS STUPIDITY with a key of k = 9 columns. Solution: We write the plaintext horizontally in 9 columns as follows: NOTHINGIN THEWORLDI SMOREDANG EROUSTHAN SINCEREIG NORANCEAN DCONSCIEN TIOUSSTUP IDITY The cipher text is therefore: NTSES NDTIO HMRIO CIDTE OONRO OIHWR UCANU TIOES ENSSY NRDTR CCSGL AHEEI TIDNA IAEUN IGNGN NP. -
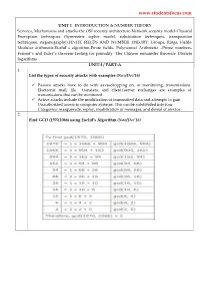
Unit I Introduction & Number Theory
www.studentsfocus.com UNIT I INTRODUCTION & NUMBER THEORY Services, Mechanisms and attacks-the OSI security architecture-Network security model-Classical Encryption techniques (Symmetric cipher model, substitution techniques, transposition techniques, steganography).FINITE FIELDS AND NUMBER THEORY: Groups, Rings, Fields- Modular arithmetic-Euclid‟s algorithm-Finite fields- Polynomial Arithmetic –Prime numbers- Fermat‟s and Euler‟s theorem-Testing for primality -The Chinese remainder theorem- Discrete logarithms. UNIT-I / PART-A 1. List the types of security attacks with examples.(Nov/Dec’16) ü Passive attacks have to do with eavesdropping on, or monitoring, transmissions. Electronic mail, file transfers, and client/server exchanges are examples of transmissions that can be monitored. ü Active attacks include the modification of transmitted data and attempts to gain Unauthorized access to computer systems. This can be subdivided into four Categories: masquerade, replay, modification of messages, and denial of service. 2. Find GCD (1970,1066) using Euclid’s Algorithm.(Nov/Dec’16) www.studentsfocus.com 3. Define Fermat & Euler’s theorem.(Apr/May’17) ü Fermat’s little theorem states that if p is a prime number, then for any integer a, not divisible by p. then ap ≡ a(mod p) ü It is the basis for primality test. ü It plays an important role in public key cryptography In number theory, Euler's theorem (also known as the Fermat–Euler theorem or Euler's theorem (also known as the Fermat–Euler theorem or Euler's totient theorem) states that if n and a are co prime positive integers, then a φ(n) ≡1(mod n) where φ(n) is Euler's totient function. -

Cryptography
Bastian | Planning & Pacing Guide UNIT 5: CRYPTOGRAPHY Estimated Time in Hours: 16-17 Big Idea(s) Enduring Understandings Projects & Major Assignments 2 Establishing Trust 2.1, 4.3, 7.2, 8.1 - Scytale & Caesar Cipher 4 Data Security - Caesar Cipher Program 7 Risk - Anagrams 8 Implications - Symmetric Ciphers - Steganography - Public Key Encryption & Digital Signatures - History & Politics of Public Key Encryption - Breakout Box Guiding Questions: • What are the ways in which data can be encrypted? • What actions can be taken to validate that data has been unaltered by an unauthorized source? Learning Objectives & Materials Instructional Activities and Classroom Assessments Respective Essential Knowledge Statements 2.1.1 LO: Students will evaluate • KWL Chart (find example Introduction to Cryptology: (1-day lesson) methods of keeping information KWL chart at This lesson introduces students to cryptography and the secret from those whom the https://www.timvandevall history of cryptography. information should be kept .com/templates/kwl- • Students begin with a pre-assessment using a KWL chart secret chart-template/ ) to identify what they know about cryptography. Students EK: 2.1.1c,d • “Cryptography: Crash then watch the Cryptography Video. Students take Course Computer Science Cornell notes on the video. Once the video is over, 4.3.1 LO: Students will define #33.” YouTube, uploaded students return to the KWL chart and add to it based on cryptography and explain how it by CrashCourse, 25 Oct what they have learned and what questions they still is used in data security. 2017, have. The class discusses the purpose of encryption, and EK: 4.3.1a,b,c,d,e,f,g,h,i https://www.youtube.c how it is necessary to ensure confidentiality and integrity. -

Grade 6 Math Circles Cryptography Introduction to Cryptography
Faculty of Mathematics Centre for Education in Waterloo, Ontario N2L 3G1 Mathematics and Computing Grade 6 Math Circles October 4 & 5, 2016 Cryptography Introduction to Cryptography Cryptography is the study of hidden writing or reading and writing secret messages or codes. The word cryptography comes from the Greek word kryptos (κρυτ&) meaning hid- den and graphein (γραφω) meaning writing. Before we get any further, let's learn some terminology: Plaintext: The original message or information the sender wants to encode or hide Encryption: The process of encrypting plaintext such that only authorized parties, such as the sender and receiver, can read it Ciphertext: The encrypted message of the plaintext that was encrypted using a cipher (the method of performing encryption) Decryption: The process of decoding ciphertext back into its original plaintext Hello World Khoor Zruog Hello Zruog Khoor Khoor Zruog World 1. Person A encrypts plaintext 2. Person B receives ciphertext 3. Person B decrypts ciphertext back into ciphertext into plaintext 1 Rail Fence Cipher Let's warm up with an easy cipher. With the rail fence cipher, we will be transposing, or changing the position of the letters in a message. To transpose a message, we need a key number and we will need to write each letter of the message up and down the rail fence. Here is an example of how the cipher works: Suppose the message is TURTLES ARE SLOW and our key number is 3. Now imagine a rail fence with 3 rails. By reading off the rows of the rail fence, the resulting ciphertext is TLRO UTEAELW RSS. -

Cryptography and Network Security Module: Transposition Cipher And
e-PGPathshala Subject : Computer Science Paper: Cryptography and Network Security Module: Transposition Cipher and Cryptanalysis Module No: CS/CNS/4 Quadrant 1 – e-text Cryptography and Network Security Module 4- Transposition Cipher and Cryptanalysis Learning Objectives ➢ To know the substitution cipher in classical cryptography ➢ To learn about the mono alphabetic substitution cipher ➢ To learn about the poly alphabetic substitution cipher ➢ Cryptanalysis of Substitution cipher 4.1 Introduction Cryptanalysis is the study of analyzing information systems in order to study the hidden aspects of the systems. Cryptanalysis is used to breach cryptographic security systems and gain access to the contents of encrypted messages, even if the cryptographic key is unknown. In addition to mathematical analysis of cryptographic algorithms, cryptanalysis includes the study of side-channel attacks that do not target weaknesses in the cryptographic algorithms themselves, but instead exploit weaknesses in their implementation. 4.2 Transposition Ciphers ➢ In transposition ciphers, we transpose (scramble) the plaintext letters Transposition (permutation) means rearranging the order of appearance of the elements of the plaintext. In other words cipher text constitutes permutation of plain text. In general transposition depends on the length of the text and it is aperiodic. – The scrambled text is the ciphertext – The transposition is the key ➢ Corresponds to Shannon’s principle of diffusion( property that spreads statistic properties of text all over the text preventing statistic analysis) – This idea is widely used in modern ciphers 4.3 Scytale ➢ One of the oldest cryptography tools was a Spartan scytale , circa 500 BC. ➢ Sender and recipient each had a rod of exactly the same radius. -

2. Classic Cryptography Methods 2.1. Spartan Scytale. One of the Oldest Known Examples Is the Spartan Scytale (Scytale /Skɪtəl
2. Classic Cryptography Methods 2.1. Spartan scytale. One of the oldest known examples is the Spartan scytale (scytale /skɪtəli/, rhymes with Italy, a baton). From indirect evidence, the scytale was first mentioned by the Greek poet Archilochus who lived in the 7th century B.C. (over 2500 years ago). The ancient Greeks, and the Spartans in particular, are said to have used this cipher to communicate during military campaigns.Sender and recipient each had a cylinder (called a scytale) of exactly the same radius. The sender wound a narrow ribbon of parchment around his cylinder, then wrote on it lengthwise. After the ribbon is unwound, the writing could be read only by a person who had a cylinder of exactly the same circumference. The following table illustrate the idea. Imagine that each column wraps around the dowel one time, that is that the bottom of one column is followed by the top of the next column. Original message: Kill king tomorrow midnight Wrapped message: k i l l k i n g t o m o r r o w m i d n i g h t Encoded message: ktm ioi lmd lon kri irg noh gwt The key parameter in using the scytale encryption is the number of letters that can be recorded on one wrap ribbon around the dowel. Above the maximum was 3, since there are 3 rows in the wrapped meassage. The last row was padded with blank spaces before the message was encoded. We'll call this the wrap parameter. If you don't know the wrap parameter you cannot decode a message. -

CS 105 - Lab 9
CS 105 - Lab 9 Today, you will be implementing three different ciphers! There's a very weak Caesar cipher, a similarly weak Transpositional cipher, and a stronger but not impenetrable Vigenere cipher. Let's get into it. Part 1: ROT13 The first cipher that we're going to implement is a simple one that is trivial to break if you know a ciphertext is using it. ROT13, also called the Caesar cipher, was developed in ancient Rome and is a simple substitution cipher. ROT13 is terrible for encryption, but is used as a classic example for weak encryption. Let's make it in Python! Open up Spyder and create a file called rot13encrypt.py. # ROT13 encrypter # define our alphabet alphabet = list('ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz') # get a phrase as user input phrase = input('Enter a phrase to encode: ') # for each character in our phrase for character in phrase: # if the character is a letter in our alphabet, shift it by 13 # and add it to our encrypted string index = alphabet.index(character) print(alphabet[index-13], end='') Run this script and input your first name only. What is the output? Try re-running the program with your first name, a space, and your last name. The program should crash. Write down the error that you receive. Why do you think the program doesn't work with punctuation such as spaces? # ROT13 encrypter # define our alphabet alphabet = list('ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz') # get a phrase as user input phrase = input('Enter a phrase to encode: ') # for each character in our phrase for character in phrase: # if the character is a letter in our alphabet, shift it by 13 # and add it to our encrypted string try: index = alphabet.index(character) print(alphabet[index-13], end='') # otherwise, add the symbol to our encrypted string without processing it except ValueError: print(character, end='') Modify the program to include try..