Quantifying Fatigue in MLB Relievers
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Miami Marlins (3-6-1) St. Louis Cardinals (7-2-1)
MIAMI MARLINS (3-6-1) (RHP Tom Koehler; 1-0, 3.00) at ST. LOUIS CARDINALS (7-2-1) (RHP Adam Wainwright; 0-0, 13.50) ROGER DEAN STADIUM, JUPITER, FL Tuesday, March 7, 2017 – 1:05 p.m. TODAY’S GAME: The Marlins and host Cardinals will meet for the third time this spring. They have not met since open- ing their Grapefruit League schedules with a home-and-home set on February 25 & 26; Miami won the opener, 8-7, TODAY’S PITCHING LINEUP before dropping the second game, 7-4. Today’s game can be seen live on FOX Sports Florida and heard in English on RHP Tom Koehler WINZ 940 AM and 94.9 HD2. LHP Kyle Lobstein LHP Matt Tomshaw TODAY’S STARTING PITCHER: Right-hander Tom Koehler will make his second start (third appearance) of the spring to- RHP Junichi Tazawa day against the Cardinals. His last outing was a start on March 1 at Houston, when he picked up the win after tossing LHP Hunter Cervenka 2.0 innings, allowing one run on one hit and two walks, with one strikeout. LHP Jarlin García RHP Jake Esch LOOKING AHEAD: The Marlins tomorrow have the first of their three off-days this spring. They return to action on Thurs- day at 1:05 when they travel to The Ballpark of the Palm Beaches to face the Nationals. Left-hander Dillon Peters is scheduled to make the start for Miami, his first of the spring; he has allowed just one hit and one walk, with a strikeout, over 3.0 scoreless innings this spring (two appearances). -

South Dakota State JACKRABBIT ATHLETICS NEWS RELEASE
South Dakota State JACKRABBIT ATHLETICS NEWS RELEASE Jackrabbit Sports Information • 2820 HPER Center • Brookings, SD 57007-1497 Baseball Contact/Assistant AD-Sports Information: Jason Hove E-mail: [email protected] Office Phone: (605) 688-4623 Mobile: (605) 695-1827 Fax: (605) 688-5999 Facebook: www.facebook.com/jackrabbit.nation Twitter: @GoJacksSDSU Website: www.GoJacks.com 2015 BASEBALL INFORMATION Jackrabbits make trek to NDSU THIS WEEK Sports Information Contact: Jason Hove May 7, 2015 BROOKINGS, S.D. — The South Dakota State University baseball team will play its final SOUTH DAKOTA STATE (28-18, 15-9) road series of the Summit League season this weekend, traveling to North Dakota State for a at NORTH DAKOTA STATE (17-26, 8-16) three-game set. 6:30 p.m. Friday • 1 p.m. Saturday • 1 p.m. Sunday Friday’s series opener is slated for a 6:30 p.m. first pitch at Newman Outdoor Field in Newman Outdoor Field • Fargo, N.D. Fargo, North Dakota. Games Saturday and Sunday are scheduled for 1 p.m. starts. All three SDSU PROBABLE STARTERS games will be broadcast locally on KJJQ 910 AM and available free of charge through the 1B Matt Johnson, So., L-R, Ankeny, Iowa (.270 avg, 4 HR, 27 RBI, 12 2B) Jackrabbit Extra media portal at GoJacks.com, with Tyler Merriam calling the play-by-play. 2B Al Robbins, Sr., L-R, West Chicago, Ill. The Jackrabbits enter the weekend 28-18 overall and in second place in the Summit (.328 avg., 1 HR, 26 RBI, .979 fielding pct.) League standings with a 15-9 mark. -

Soonersports.Com
OKLAHOMA STAFF sunny golloway www.soonersports.com 59 2009 OKLAHOMA BASEBALL MEDIA GUIDE ELLIOTT BLAIR HEAD COACH SUNNY GOLLOWAY Head Coach | Fifth Year at Oklahoma (127-78-1) 29 HEAD COACH Sunny Golloway has led the Sooners to three NCAA Regional Finals, 127 victories and a top 25 rank- 13th year, 462-234-1 (.664) career record ing in each season during his four years at the helm of the OU program. In 2008, OU returned to the NCAA Tournament for the 31st time in program history, two years after Golloway became the second COACHING HISTORY coach in NCAA Division I history to guide his club to a Super Regional Appearance in his fi rst year at Oklahoma, head coach 2005-present the helm. The 2006 season was highlighted by the Sooners’ 45-22 overall mark, a third-place fi nish in Oklahoma, assistant coach 2004-05 the Big 12 and an NCAA regional title, a program fi rst since 1995. Oral Roberts, head coach 1996-2003 Team USA, assistant coach 2002 The Sooners posted a 36-26-1 overall record during the 2008 campaign and advanced to the cham- Kenai Peninsula Oilers, head coach 1993-95 pionship game of the NCAA Tempe Regional. Three Sooners, Aljay Davis, Aaron Baker and Mike Gosse Oklahoma, assistant coach 1992-95 were named to the all-tournament team giving OU 13 such honorees since Golloway took over at the end of the 2005 season (only four Sooners were honored in OU’s previous three appearances). COACHING ACCOMPLISHMENTS - Head coach of 2006 Regional Champions at Oklahoma Including eight seasons (1996-2003) as the head coach at Oral Roberts and his record at OU’s helm, Golloway is 462-234-1 (.664). -

NCAA Division I Baseball Records
Division I Baseball Records Individual Records .................................................................. 2 Individual Leaders .................................................................. 4 Annual Individual Champions .......................................... 14 Team Records ........................................................................... 22 Team Leaders ............................................................................ 24 Annual Team Champions .................................................... 32 All-Time Winningest Teams ................................................ 38 Collegiate Baseball Division I Final Polls ....................... 42 Baseball America Division I Final Polls ........................... 45 USA Today Baseball Weekly/ESPN/ American Baseball Coaches Association Division I Final Polls ............................................................ 46 National Collegiate Baseball Writers Association Division I Final Polls ............................................................ 48 Statistical Trends ...................................................................... 49 No-Hitters and Perfect Games by Year .......................... 50 2 NCAA BASEBALL DIVISION I RECORDS THROUGH 2011 Official NCAA Division I baseball records began Season Career with the 1957 season and are based on informa- 39—Jason Krizan, Dallas Baptist, 2011 (62 games) 346—Jeff Ledbetter, Florida St., 1979-82 (262 games) tion submitted to the NCAA statistics service by Career RUNS BATTED IN PER GAME institutions -

* Text Features
The Boston Red Sox Saturday, September 23, 2017 * The Boston Globe Red Sox put new formula to work in win over Reds Peter Abraham CINCINNATI — The Red Sox were up by a run after four innings against the Cincinnati Reds on Friday night and Rick Porcello had thrown only 57 pitches. His performance had been erratic, the righthander putting eight men in base. But Porcello expected he would stay in the game because that is what managers traditionally do, they let starting pitchers try to hold a lead. But most managers do not have a pitcher of David Price’s caliber in the bullpen and John Farrell does. Farrell turned to Price in the fifth inning and he handed that lead over to Addison Reed with two outs in the seventh. Craig Kimbrel took over in the ninth and the Sox beat the Reds, 5-4. It was a dress rehearsal for the playoffs, the Sox using Price for multiple innings to get to Reed and Kimbrel. That combination can be as good if not better than what any other playoff team has. “You saw it last year in the playoffs, so many starters went five innings or even less. You need that guy to bridge the gap,” Reed said. “When that guy is David Price, it doesn’t get much better. We’re pretty damn excited to have him down there.” With the Yankees losing in Toronto, the Sox now lead the American League East by four games with nine games to play. “The ball’s in our court. -

Peter Gammons: the Cleveland Indians, Best Run Team in Professional Sports March 5, 2018 by Peter Gammons 7 Comments PHOENIX—T
Peter Gammons: The Cleveland Indians, best run team in professional sports March 5, 2018 by Peter Gammons 7 Comments PHOENIX—The Cleveland Indians have won 454 games the last five years, 22 more than the runner-up Boston Red Sox. In those years, the Indians spent $414M less in payroll than Boston, which at the start speaks volumes about how well the Indians have been run. Two years ago, they got to the tenth inning of an incredible World Series game 7, in a rain delay. Last October they lost an agonizing 5th game of the ALDS to the Yankees, with Corey Kluber, the best pitcher in the American League hurt. They had a 22 game winning streak that ran until September 15, their +254 run differential was 56 runs better than the next best American League team (Houston), they won 102 games, they led the league in earned run average, their starters were 81-38 and they had four players hit between 29 and 38 homers, including 29 apiece from the left side of their infield, Francisco Lindor and Jose Ramirez. And they even drew 2.05M (22nd in MLB) to the ballpark formerly known as The Jake, the only time in this five year run they drew more than 1.6M or were higher than 28th in the majors. That is the reality they live with. One could argue that in terms of talent and human player development, the growth of young front office talent (6 current general managers and three club presidents), they are presently the best run organization in the sport, especially given their financial restraints. -

Cincinnati Reds'
Cincinnati Reds Press Clippings February 23, 2017 THIS DAY IN REDS HISTORY 1995 - Kevin Mitchell signs a contract to play for the Daiei Hawks in Japan. Mitchell spent three seasons with the Reds, batting .332 with 50 doubles, 55 home runs and 167 RBI MLB.COM 'Breaking' news: Cingrani develops cutter Reds lefty works in offseason to add another pitch offering By Mark Sheldon / MLB.com | @m_sheldon | February 22nd, 2017 + 50 COMMENTS GOODYEAR, Ariz. -- Reds left-hander Tony Cingrani can throw his four-seam fastball 95 mph, and consistent with his career, he used it often in 2016. It was so often that PITCHf/x data showed he threw his fastball more than 87 percent of the time. Cingrani started using a split-fingered fastball sometime in the second half, but he realized it was time to diversify the repertoire even more. He needed a breaking ball and used the offseason to develop a cut fastball. "It's just another way to get guys out," Cingrani said. "It gets hitters off thinking it's just going to be a fastball. I'm still trying to work on how I want that ball to move, but it's good and feels comfortable." At the suggestion of teammate and fellow reliever Caleb Cotham, Cingrani traveled to Kent, Wash., in the fall and worked out at Driveline Baseball. The facility, owned by Kyle Boddy, has gained a reputation for providing data-driven pitch training and also encourages building arm strength by playing catch with weighted balls. "Caleb is a pretty smart cat," Cingrani said. -

Sunday, June 6, 2021 - 1:05 P.M
Jacksonville Jumbo Shrimp (18-11) at Gwinnett Stripers (15-14) vs. THE STRIPERS 2021 vs. Stripers ..................................................................4-1 Sunday, June 6, 2021 - 1:05 p.m. ET in Jacksonville .............................................................0-0 Game No. 30 • Road Game No. 18 in Gwinnett .................................................................4-1 Coolray Field • Lawrenceville, Ga. Since 2021 vs. Gwinnett ........................................4-1 (.800) MiLB.tv • ESPN 690 AM • JaxShrimp.com • MiLB First Pitch App 2020 vs. Stripers ..................................................................0-0 in Jacksonville .............................................................0-0 RHP Parker Bugg (1-0, 3.29 ERA) vs. RHP Jasseel De La Cruz (0-0, 3.12 ERA) in Gwinnett .................................................................0-0 JUMBO SHRIMP BATTLE FOR 8-5 WIN IN 11 LET THE GOOD TIMES ROLL JUMBO SHRIMP BY THE NUMBERS Jesús Sánchez, Chad Wallach and Lewin Díaz each homered Jacksonville suffered through a season-long six-game losing Record ...............................................................................18-11 on Saturday and the Jacksonville Jumbo Shrimp fought streak from May 23-29, with the Jumbo Shrimp being Home Record .......................................................................5-7 through some late-inning adversity to beat the Gwinnett outscored by a whopping 41-10 margin by their opponents Road Record ..................................................................... -

2017 Information & Record Book
2017 INFORMATION & RECORD BOOK OWNERSHIP OF THE CLEVELAND INDIANS Paul J. Dolan John Sherman Owner/Chairman/Chief Executive Of¿ cer Vice Chairman The Dolan family's ownership of the Cleveland Indians enters its 18th season in 2017, while John Sherman was announced as Vice Chairman and minority ownership partner of the Paul Dolan begins his ¿ fth campaign as the primary control person of the franchise after Cleveland Indians on August 19, 2016. being formally approved by Major League Baseball on Jan. 10, 2013. Paul continues to A long-time entrepreneur and philanthropist, Sherman has been responsible for establishing serve as Chairman and Chief Executive Of¿ cer of the Indians, roles that he accepted prior two successful businesses in Kansas City, Missouri and has provided extensive charitable to the 2011 season. He began as Vice President, General Counsel of the Indians upon support throughout surrounding communities. joining the organization in 2000 and later served as the club's President from 2004-10. His ¿ rst startup, LPG Services Group, grew rapidly and merged with Dynegy (NYSE:DYN) Paul was born and raised in nearby Chardon, Ohio where he attended high school at in 1996. Sherman later founded Inergy L.P., which went public in 2001. He led Inergy Gilmour Academy in Gates Mills. He graduated with a B.A. degree from St. Lawrence through a period of tremendous growth, merging it with Crestwood Holdings in 2013, University in 1980 and received his Juris Doctorate from the University of Notre Dame’s and continues to serve on the board of [now] Crestwood Equity Partners (NYSE:CEQP). -

South Dakota State University Fall Senior Prospect Camps
2019 SDSU Baseball Fall Senior Prospect South Dakota State University Camp Registration Form Fall Senior Prospect Camps Name: _______________________________________________ Where: Erv Huether Field Parent / Guardian: ______________________________________ South Dakota State University SDSU Baseball Highlights Home Address: ________________________________________ o 2017 MLB Draftee, Luke Ringhofer (22nd Round, 668 Overall, When: Fall Senior Prospect Camp Dates Baltimore Orioles) City: ______________________ State: ______ Zip: __________ Saturday, August 17, 2019 o 2015 MLB Draftees, Zach Coppola (13th Round, 384 Overall, or Phone #: _____________________ DOB: ____/_____/______ Philadelphia Phillies) & Adam Bray (33rd Round, 1,002 Overall, Sunday, August 18, 2019 Email: _______________________________________________ Los Angeles Dodgers) o 2013 MLB Draftee, Layne Somsen (22nd Round, 675 Overall, Current School: ______________________ Grad. Yr. _________ Time: 8:30 AM to End of Camp (3:00 - 6:00 PM) Cincinnati Reds) MLB Debut May 14th, 2016 Primary Position: ____ Secondary Position: ____ Bat/Throw: __/__ o 2013 Summit League Tournament Champions and Regional Who: 2020 Grads (Underclassmen welcome by request) Tournament Appearance GPA: _____/4.0 ACT:_____ T-Shirt Size: _____ o 2011 MLB Draftee, Blake Treinen (7th Round, 226 Overall, (Guaranteed T-Shirt Size if Registered by 8/1/19) Cost: $160 Position Player or $100 Pitcher Only Oakland Athletics) MLB Debut April 12th, 2014 (with Nationals) th Fall Senior Prospect Camp Registration Early -

Castrovince | October 23Rd, 2016 CLEVELAND -- the Baseball Season Ends with Someone Else Celebrating
C's the day before: Chicago, Cleveland ready By Anthony Castrovince / MLB.com | @castrovince | October 23rd, 2016 CLEVELAND -- The baseball season ends with someone else celebrating. That's just how it is for fans of the Indians and Cubs. And then winter begins, and, to paraphrase the great meteorologist Phil Connors from "Groundhog Day," it is cold, it is gray and it lasts the rest of your life. The city of Cleveland has had 68 of those salt-spreading, ice-chopping, snow-shoveling winters between Tribe titles, while Chicagoans with an affinity for the North Siders have all been biding their time in the wintry winds since, in all probability, well before birth. Remarkably, it's been 108 years since the Cubs were last on top of the baseball world. So if patience is a virtue, the Cubs and Tribe are as virtuous as they come. And the 2016 World Series that arrives with Monday's Media Day - - the pinch-us, we're-really-here appetizer to Tuesday's intensely anticipated Game 1 at Progressive Field -- is one pitting fan bases of shared circumstances and sentiments against each other. These are two cities, separated by just 350 miles, on the Great Lakes with no great shakes in the realm of baseball background, and that has instilled in their people a common and eventually unmet refrain of "Why not us?" But for one of them, the tide will soon turn and so, too, will the response: "Really? Us?" Yes, you. Imagine what that would feel like for Norman Rosen. He's 90 years old and wise to the patience required of Cubs fandom. -
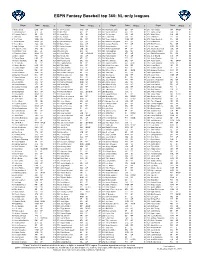
NL-Only Leagues
ESPN Fantasy Baseball top 360: NL-only leagues Player Team All pos. $ Player Team All pos. $ Player Team All pos. $ Player Team All pos. $ 1. Mookie Betts LAD OF $44 91. Joc Pederson CHC OF $14 181. MacKenzie Gore SD SP $7 271. John Curtiss MIA RP/SP $1 2. Ronald Acuna Jr. ATL OF $39 92. Will Smith ATL RP $14 182. Stefan Crichton ARI RP $6 272. Josh Fuentes COL 1B $1 3. Fernando Tatis Jr. SD SS $37 93. Austin Riley ATL 3B $14 183. Tim Locastro ARI OF $6 273. Wade Miley CIN SP $1 4. Juan Soto WSH OF $36 94. A.J. Pollock LAD OF $14 184. Lucas Sims CIN RP $6 274. Chad Kuhl PIT SP $1 5. Trea Turner WSH SS $32 95. Devin Williams MIL RP $13 185. Tanner Rainey WSH RP $6 275. Anibal Sanchez FA SP $1 6. Jacob deGrom NYM SP $30 96. German Marquez COL SP $13 186. Madison Bumgarner ARI SP $6 276. Rowan Wick CHC RP $1 7. Trevor Story COL SS $30 97. Raimel Tapia COL OF $13 187. Gregory Polanco PIT OF $6 277. Rick Porcello FA SP $0 8. Cody Bellinger LAD OF/1B $30 98. Carlos Carrasco NYM SP $13 188. Omar Narvaez MIL C $6 278. Jon Lester WSH SP $0 9. Freddie Freeman ATL 1B $29 99. Gavin Lux LAD 2B $13 189. Anthony DeSclafani SF SP $6 279. Antonio Senzatela COL SP $0 10. Christian Yelich MIL OF $29 100. Zach Eflin PHI SP $13 190. Josh Lindblom MIL SP $6 280.