Characterizations of Classes of Harmonic Convex Functions and Applications
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Self Discovery with Talent Management Achieving Excellence in Your Professional Career Resource Person: Engr
Webinar Titled: Self Discovery With Talent Management Achieving Excellence in Your Professional Career Resource Person: Engr. Prof. Dr. Bhawani Shankar Chowdhry Dated: 7-5-2021 Certificate Sr# PEC Reg No. Name CPD Points Serial 1 54551 CIVIL/50600 Muhammad Zahid Saeed 0.5 2 54552 CIVIL/49863 Muhammad Safeer 0.5 3 54553 CIVIL/50354 Aftab Alam 0.5 4 54554 CIVIL/49741 Shayan Afsar 0.5 5 54555 MECH/39680 Salim Akhtar 0.5 6 54556 TEXTILE/03066 rajesh kumar 0.5 7 54557 ELECT/70876 Muhammad Luqman 0.5 8 54558 CHEM/17296 MUHAMMAD ANUS 0.5 9 54559 CIVIL/49460 Abdul Qadeer 0.5 10 54560 CIVIL/50304 SYED YASIR HUSSAIN 0.5 11 54561 MECH/39528 Abubakr Shahnawaz Kamil 0.5 12 54562 CIVIL/49536 Allah Yar Khan 0.5 13 54563 CHEM/17535 SHAHBAZ AHMED KHAN 0.5 14 54564 METAL/05179 FAHIM ULLAH JAN 0.5 15 54565 ELECT/72503 Sabien irshad 0.5 16 54566 CIVIL/49494 MUHAMMAD ZEESHAN 0.5 17 54567 ELECTRO/27870 Rehan Ali Hasani 0.5 18 54568 ELECT/71041 M Hamza Ahmad 0.5 19 54569 CIVIL/50569 Hafiz Zeeshan Zia 0.5 20 54570 CIVIL/49986 SHAHZADA MUHAMMAD ZULQERNAIN 0.5 21 54571 AGRI/05372 Faiz Ul Haq 0.5 22 54572 AGRI/05368 MUHAMMAD HAMZA 0.5 23 54573 CIVIL/49529 Rizwan Muhammad 0.5 24 54574 CIVIL/49604 Shahid Saeed 0.5 25 54575 METAL/05231 FARHAN ALI 0.5 26 54576 AGRI/05417 Muhammad Luqman ur Rehman 0.5 27 54577 MECH/39060 Muhammad Muddasar 0.5 28 54578 ELECT/71685 Waqar Ahmed 0.5 29 54579 TRANSPORT/00326 Muhammad Arslan Ali 0.5 30 54580 MECH/38930 Ghulam Yaseen 0.5 31 54581 CIVIL/49470 Haider Abbas 0.5 32 54582 ELECT/71683 ASAD ALI 0.5 33 54583 CIVIL/49445 Abdul Haseeb -
Updated As on 18Aug20.Xlsx
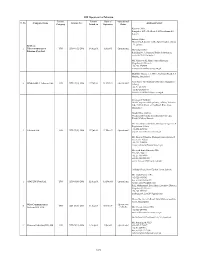
LDI Oprators for Pakistan License License Date of Operational S. No. Company Name License No. Address/Contact Category Issued on Operation Status Karachi Office: Bungalow # D – 23, Block 2, KDA Scheme # 5, Karachi Lahore Office: House # 4-B, Justice Sardar Iqbal Road, Gulberg – V, Lahore REDtone 1 Telecommunication LDI LDI-06(02)-2004 16-Aug-04 14-Jan-05 Operational Islamabad Office: Pakistan (Pvt.) Ltd. Building No. 9, National Police Foundation, Sector E-11/4 Islamabad Mr. Mansoor Ali Khan, Senior Manager (Regulatory Affaires) +92-300-8528874 [email protected] Mobilink House, 1-A, IBC-1, Kohistan Road, F-8 Markaz, Islamabad Syed Naser Ali Hamdani, Director (Regulatory 2 LINKdotNET Telecom Ltd. LDI LDI-03(03)-2004 17-Jul-04 30-May-06 Operational Affairs) +92-51-2817579 +92-51-2817533-39 [email protected] Coorporate Address Head Corporate & Regulatory Affairs, Telecard Ltd., 75-East, Fazal-e-Haq Road, Blue Area, Islamabad Head Office Address World Trade Center, 10, Khayban-e-Roomi, Block-5,Clifton, Karachi Mr. Fawad Naeem Bhatti, Manager Corporate & Regulatory Affairs +92-322-4473900 3 Telecard Ltd. LDI LDI-07(06)-2004 27-Jul-04 17-Mar-05 Operational [email protected] Mr. Rizwan Cheema, Manager Interconnects & Corporate Affairs +92-333-5180032 [email protected] Mr. Syed Amir Hussain, CEO +92-346-2044777 +92-21-38330000 +92-21-111-222-123 [email protected] 19 Babar Block, New Garden Town, Lahore Mr. Abdul Sattar, CFO +92-321-8838383 Fax: +92-42-35834021 4 ADG LDI (Pvt.) Ltd. LDI LDI-08(08)-2004 12-Aug-04 14-Dec-04 Operational [email protected] Brig. -

MEI Report Sunni Deobandi-Shi`I Sectarian Violence in Pakistan Explaining the Resurgence Since 2007 Arif Ra!Q
MEI Report Sunni Deobandi-Shi`i Sectarian Violence in Pakistan Explaining the Resurgence Since 2007 Arif Ra!q Photo Credit: AP Photo/B.K. Bangash December 2014 ! Sunni Deobandi-Shi‘i Sectarian Violence in Pakistan Explaining the Resurgence since 2007 Arif Rafiq! DECEMBER 2014 1 ! ! Contents ! ! I. Summary ................................................................................. 3! II. Acronyms ............................................................................... 5! III. The Author ............................................................................ 8! IV. Introduction .......................................................................... 9! V. Historic Roots of Sunni Deobandi-Shi‘i Conflict in Pakistan ...... 10! VI. Sectarian Violence Surges since 2007: How and Why? ............ 32! VII. Current Trends: Sectarianism Growing .................................. 91! VIII. Policy Recommendations .................................................. 105! IX. Bibliography ..................................................................... 110! X. Notes ................................................................................ 114! ! 2 I. Summary • Sectarian violence between Sunni Deobandi and Shi‘i Muslims in Pakistan has resurged since 2007, resulting in approximately 2,300 deaths in Pakistan’s four main provinces from 2007 to 2013 and an estimated 1,500 deaths in the Kurram Agency from 2007 to 2011. • Baluchistan and Karachi are now the two most active zones of violence between Sunni Deobandis and Shi‘a, -

Page 01 Jan 12.Indd
3rd Best News Website in the Middle East BUSINESS | 18 SPORT | 24 Brexit: May In-form Qatar too ggoo meets top all out for victoryry financiers against Oman Friday 12 January 2018 | 25 Rabia II I 1439 www.thepeninsula.qa Volume 22 | Number 7404 | 2 Riyals 1,000 world experts Defence Minister attends Military College graduation discuss cardiac care FAZEENA SALEEM The three-day conference, THE PENINSULA attended by over 1,000 eminent experts across the DOHA: Over 1,000 cardiology experts across the globe gathered at the 14th Gulf globe, is discussing advanced Heart Association Conference and the 11th treatment methods in the Gulf Vascular Society Symposium that field of cardiology. began yesterday in the presence of Minister of Public Health H E Dr Hanan Mohamed Al Kuwari. The Minister also inaugurated Dr Jeroen Bax, President of European an exhibition being held on the sidelines Society of Cardiology, and Dr David Wood, of the conference at the Sheraton Grand President of World Health Federation Doha Resort and Convention Hotel. addressed the opening session. The three-day conference is discussing Dr Amr Badr, Consultant, Cardiology, advanced treatment methods in the field Hamad Medical Corporation and Director The Ahmed bin Mohammed Military College celebrated the handing out of graduation certificates to 124 candidates of cardiology. There are several sessions Of Heart Failure Clinic , speaking to media of the 13th batch at the college’s educational building. The ceremony was held under the patronage of Deputy Prime and workshops that will provide partici- on the sidelines said that the issues that pants with information on comprehensive will be discussed during the conference Minister and Minister of State for Defence Affairs H E Dr Khalid bin Mohamed Al Attiyah and in the presence of Chief approaches to the prevention, diagnosis, will improve patient care. -

Jahangir Siddiqui & Co. Ltd. List of Shareholders (Unclaimed Dividend
Page 1 of 83 Jahangir Siddiqui & Co. Ltd. List of Shareholders (Unclaimed Dividend) Unclaimed S. No. Name of Shareholder Address Dividend (PKR) 1 (1081) MRS. LAILA NUSRAT 17-B, JUSTICE SARDAR IQBALROAD, GULBERG-III, LAHORE. 56 2 (1329) BURHAN ALI 341/B,NEW CHOUBURJI PARK,LAHORE. 90 3 (1350) MUBARIK ALI C/O ROOM#509, LAHORE STOCKEXCHANGE BUILDING, LAHORE. 450 4 (1538) MALIK MUHAMMAD ALEEM HOUSE#12, MAIN BAZAR QILLAGUJAR SINGH, LAHORE. 425 5 (1746) MUHAMAMD SALEEM BASHIR H.#17, S.#3, D-BLOCK MALIKMUNIR ROAD GULSHAN RAVILAHORE. LAHORE 650 6 (1746) MUHAMAMD SALEEM BASHIR H.#17, S.#3, D-BLOCK MALIKMUNIR ROAD GULSHAN RAVILAHORE. LAHORE 425 7 (1832) QAZI ZUBAIR GILL H.#26, S.#2, NADEEM PARK,NEW SHALIMAR TOWN, LAHORE. 340 8 (1882) MUHAMMAD AKRAM KHAN 185-KAMRAN BLOCK ALLAMAIQBAL TOWN, LAHORE. 128 9 (1944) MAZHAR MUNIR H.#94, ALALH RAKHA STREETSAIF ROAD,BHAGAT PURA SHADBAGHLAHORE. LAHORE 425 10 (2056) WAQAS AHMAD KALEEM 202-G/1, JOHAR TOWN,LAHORE 657 11 (2064)SANA UD DIN QURESHI HOUSE#1-1016, KUCHA KAMANGARAN RANG MAHAL, LAHORE. 650 12 (2067) MRS.RAFIA JAMAL AMJID HUSSAIN MUGHAL,QYARTER#10/61 SODEEWAL COLONY,MULTAN ROAD LAHORE 65 13 (2159) MUHAMMAD ALTAF BURJ ATTARI FEROZ WALADISTRICT SHEIKHUPURA 292 14 (2178) ZEESHAN MUSTAQ HOUSE# 279/A STREET#01,TAYYABA COLONY BHAGATPURASHAD BAGH LAHORE 353 15 (2244) GHAZANFAR ABBAS CHUGHTAI C/O MAQBOOL AHMAD STREET#05,QUAD-E-MILLAT COLONY GHUNGI AMAR 1,560 16 (2331) DILAWER HUSSAIN E-361 RAJAB ABAD BEDIAN ROAD,LAHORE CANTT 325 17 (2346) MUHAMMAD IMRAN AFZAL GOLDEN NUSERY, 9-SHALIMAR LINKROAD OPP.BOC GAS FACTORY,MUGHALPURA LAHORE 85 18 (786) M. -

Islamabad.Xlsx
GOVERNMENT OF PAKISTAN PLANNING COMMISSION MINISTRY OF PLANNING DEVELOPMENT & SPECIAL INITIATIVES *-*-*-*-* List of Candidates for the Post of Assistant (BS-15) COMSATS UNIVERSITY, ISLAMABAD Sr. No. Roll No Name Father's Name 1970 AI - 01 Aamir Khan Malik Abdul Maalik 743 AI - 02 Aamir Khurshid Khurshid Ahmad 283 AI - 03 Aamna Bashir Muhammad Bashir 2534 AI - 04 Aaqib Naeem Muhammad Naeem 281 AI - 05 Aashar Hussain Tassadaq Hussain 2532 AI - 06 Abbas Ahmad Muhammad Yousaf 7318 AI - 07 ABDUL BASIT MUHAMMAD YOUSAF 3449 AI - 08 ABDUL BASIT KHAN Rais Ahmad Khan 6909 AI - 09 ABDUL BASIT QURESHI Gulzar Ahmed Qureshi 4940 AI - 10 ABDUL FATTAH Amanullah 2564 AI - 11 Abdul Haq Abdul Rasheed 3960 AI - 12 ABDUL HASEEB Rahman Ud Din 8091 AI - 13 ABDUL HASEEB RANA Abdul Jabbar 7862 AI - 14 ABDUL JABBAR Haji Jan Muhammad 1595 AI - 15 Abdul Jabbar Qayyum Abdul Qayyum Abbasi 2202 AI - 16 Abdul Khaliq Hazoor Bux 6666 AI - 17 ABDUL MANAN Muhammad Aslam 3376 AI - 18 ABDUL MATEEN Abdul Rauf 3798 AI - 19 ABDUL MUQEET Ashiq Hussain Bhatti 930 AI - 20 Abdul Qudoos Raza Muhammad 5814 AI - 21 ABDUL RAHMAN Abdul Fatah 2993 AI - 22 ABDUL RAZZAQ Qurban Ali 499 AI - 23 Abdul Rehman Ejaz Ahmad 3203 AI - 24 ABDUL ROUF GHULAM RASOOL 5166 AI - 25 ABDUL SAEED BHUTTO Abdul Jabbar Bhutto 3786 AI - 26 ABDUL SAMAD Abdul Rashid 5699 AI - 27 ABDUL SAMAD RIAZ AHMED KHAN 2525 AI - 28 Abdul Samad Khan Abdul Rahim Khan 2197 AI - 29 Abdul Shakoor Shah Muhammad 2476 AI - 30 Abdul Shakoor Sohor Ghulam Murtaza 186 AI - 31 Abdul Subhan Khan Muhammad Arif Khan 2446 AI - 32 Abdul Wahab -

Pakistan Society of Development Economists
Pakistan Society of Development Economists Pakistan Institute of Development Economics Quaid-i-Azam University Campus, PO Box 1091, Islamabad, Pakistan List of Invited Students at the 23rd AGM-PSDE, Islamabad Please find your name in the list given below. Listed students (out-station/local) are welcome to participate in the 23rd AGM–PSDE, Islamabad. For others, we regret to inform you that due to limited funds, this year, we can not offer you the place/stipend. We wish that all of you will get the chance to attend the 24th AGM-PSDE. Invited student(s): You are welcome to attend the 23rd Annual General Meeting and Conference of the Pakistan Society of Development Economists (AGM– PSDE) during March 12th-14th, 2008, at Marriott Hotel Islamabad. Please read the following instructions carefully: 1. Students will register at the students’ reception desk, Marriott Hotel, Islamabad, on the 12th March, 2008, before 9:00 a.m. 2. Please bring your (original) Student Identity Card and National Identity Card (CNIC) 3. Every student is requested to put on his/her attendance twice a day at the students’ desk, i.e., at 8:45 a.m. and 4:00 p.m. 4. A total of Rs.2100/- 1 or Rs. 3000/- 2 will be paid to each student on the 14th March, 2008, with a compulsory condition to his/her attendance in the conference sessions. 5. Students are responsible for their travel arrangements and overnight stay, PIDE has no liability underlining the logistics and security issues. 6. Students will be given the same standard as of other participants, i.e., they will be offered high-teas and lunch during conference sessions, and conference material 7. -
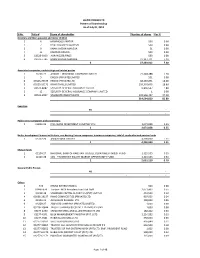
Lalpir SHAREHOLDING PATTERN-31-07-2013AFTER
LALPIR POWER LTD Pattern of Shareholding As of July 31, 2013 S.No. Folio # Name of shareholder Number of shares Per % Directors and their spouse(s) and minor children 1 6 MAHMOOD AKHTAR 550 0.00 2 7 KHALID QADEER QURESHI 550 0.00 3 9 MIAN HASSAN MANSHA 51 0.00 4 11 KAMRAN RASOOL 500 0.00 5 03525‐3993 AURANGZEB FIROZ 550 0.00 6 03525‐5745 MIAN HASSAN MANSHA 27,347,711 7.20 6 27,349,912 7.20 Associated companies, undertakings and related parties 7 13755‐21 ADAMJEE INSURANCE COMPANY LIMITED 27,348,388 7.20 1 5 ENGEN (PRIVATE) LIMITED 551 0.00 6 03525‐75375 ENGEN (PRIVATE) LTD 68,369,871 18.00 5 03525‐35171 NISHAT MILLS LIMITED 109,393,005 28.80 4 03525‐8082 SECURITY GENERAL INSURANCE CO LTD 6,836,547 1.80 2 12 SECURITY GENERAL INSURANCE COMPANY LIMITED 1 0.00 3 00521‐3837 STANHOPE INVESTMENTS 102,556,457 27.00 7 314,504,820 82.80 Executive NIL ‐ ‐ ‐ ‐ Public sector companies and corporations 1 04812‐24 PAK‐OMAN INVESTMENT COMPANY LTD. 2,071,858 0.55 1 2,071,858 0.55 Banks, development finance institutions, non‐banking finance companies, insurance companies, takaful, modarabas and pension funds 1 05132‐26 ASKARI BANK LIMITED 4,200,000 1.11 1 4,200,000 1.11 Mutual Funds 1 02154‐27 NATIONAL BANK OF PAKISTAN‐TRUSTEE DEPARTMENT NI(U)T FUND 1,325,555 0.35 2 12120‐28 CDC ‐ TRUSTEE NIT‐EQUITY MARKET OPPORTUNITY FUND 1,325,555 0.35 2 2,651,110 0.70 General Public Foreign NIL ‐ ‐ ‐ ‐ Others 1 774 EHSAN INTERNATIONAL 500 0.00 2 01446‐874 Trustee ‐ MCB Provident Fund Pak Staff 2,071,402 0.55 3 03038‐38 STANDARD CAPITAL SECURITIES (PVT) LIMITED 453,500 0.12 4 03038‐19137 RANG COMMODITIES (PRIVATE) LTD 907,000 0.24 5 03103‐21 ALI HUSAIN RAJABALI LTD 200,000 0.05 6 03228‐27 ABBASI & COMPANY (PRIVATE) LIMITED 1,000 0.00 7 03228‐10844 TRUSTEES‐ABBASI & CO.PVT.LTD.EMPS.P.FUND 1,000 0.00 8 03277‐4230 CRESCENT STEEL AND ALLIED PRODUCTS LTD. -

Baghlan Hostages Released by Taliban After 48 Hours
Eye on the News [email protected] Truthful, Factual and Unbiased Vol:X Issue No:09 Price: Afs.15 www.afghanistantimes.af www.facebook.com/ afghanistantimeswww.twitter.com/ afghanistantimes THURSDAY . JULY 30 . 2015 -Asad 08, 1394 HS LeJ chief NSC seeks Malik Ishaq international Page 4 killed in Muzaffargarh COOPERATION police IN FIGHT AGAINST ISIS AT Monitoring Desk Turkey KABUL: The National Security inks deal Mullah Omar s death in a hospital in Karachi city of Pakistan is still in mystery, Siddiqui Council (NSC) stressed on region- al and international cooperation in to open fight against ISIS. Najib Manalai, Page 5 bases to Abdul Zuhoor Qayomi the cultural advisor to the NSC, told Azadi Radio that ISIS has never US-led been strong in Afghanistan, but its KABUL: The National Director- presence is a threat to the country. coalition ate of Security (NDS) confirmed He stressed that the entire world that Taliban s leader Mullah Omar should take part in fight against died around two years and four ISIS, also known as Daesh. Qatar Airways, months ago in a hospital in Kara- Some senior commanders of chi city of Pakistan. Daesh have been killed in Afghan- Flydubai Abdul Haseeb Siddiqui, istan over the past few months. reject reports spokesman for the NDS, said that The National Directorate of Secu- Mullah Omar mysteriously died rity (NDS) said that killing of the Page 9 of interest in in a hospital in Karachi around two ISIS commanders has weakened the India s years and four months ago. He terrorist group in Afghanistan. The said that Mullah Omar s death is secretary of Meshrano Jirga, Naji- SpiceJet still a mystery. -

Gold Medal Winners 2010
GOLD MEDAL WINNERS TOP IN PAKISTAN S.# Roll No Student Name Father Name Class Institution 1 10-021-01773-12-010 ARSALAN ALI GOHAR JUMANI ALI GOHAR JUMANI 12 THE OASYS SCHOOL, C-53, BLOCK-2, CLIFTON, KARACHI 2 10-51-01777-11-012 REDA ZAINAB KHALID KHALID MATEEN KHAN 11 ROOTS SCHOOL SYSTEM, FIRST AVENUE, SECTOR-A, DHA PHASE-I, ISLAMABAD 3 10-051-01103-10-001 WAQAS AKMAL BUTT MUHAMMAD AKMAL BUTT 10 THE CITY SCHOOL CAPITAL CAMPUS ISLAMABAD, PITRAS BOKHARI ROAD H-8/1, ISLAMABAD 4 10-051-01709-9-003 MUAHMMAD TAIMUR BIN ANJUM MUHAMMAD ANJUM BASHIR 9 OPF BOYS COLLEGE, H - 8/4 ISLAMABAD 5 10-021-00573-8-009 MOHAMMAD DANIYAL ALI ALI JUNE AGHA 8 KARACHI GRAMMAR SCHOOL MIDDLE SECTION, 94 DEPOT LINES SADDAR P.O. BOX 7198KARACHI 6 10-91-00893-7-005 WALEED FARMAN ALI SHAH 7 PAKTURK INTERNATIONAL COLLEGES AND SCHOOLS PESHAWAR BRANCH, NEAR PASSPORT OFFICE PHASE 5 HAYATABAD 7 10-42-00904-6-007 MINAHIL RAZA RAZA HUSSAIN 6 LAHORE GRAMMAR SCHOOL, 286-II-C/I, TOWNSHIP LAHORE 8 10-021-01710-6-036 RAYYAN-UL-HAQ IRFAN-UL-HAQ 6 BAI VIRBAIJI SOPARIVALA PARSI HIGH SCHOOL, MAIN ABDULLAH HAROON ROAD , SADDAR , KRACHI 74400 9 10-606-00934-6-010 SAAD KHAN MUHAMMAD ISMAEEL 6 KIDS UNIVERSITY, 22-EMPLOYEES COLONY LAYYAH 10 10-42-00565-5-003 HAMID AFZAAL AFZAAL AHMAD 5 DIVISIONAL PUBLIC SCHOOL & INTERMEDIATE COLLEGE, H, BLOCK, MODEL TOWN, LAHORE. 11 10-51-01789-4-013 VANEEZA QADEER ABDUL QADEER KHAN 4 ROOTS SCHOOL SYSTEM, 15 - TULSA ROAD, LALAZAR 12 10-51-01789-4-025 IZZA NADEEM MALIK NADEEM YOUNAS 4 ROOTS SCHOOL SYSTEM, 15 - TULSA ROAD, LALAZAR 13 10-51-01791-4-013 ABDULLAH AFGAN SHER AFGAN 4 ROOTS SCHOOL SYSTEM, 15-HARLEY STREET RAWALPINDI 14 10-48-01760-4-045 MUHAMMAD MOAZ MUNIR MUHAMMAD MUNIR AHMAD 4 ISLAMIC ALTA VISTA HIGH HCHOOL, 220 - A SATELLITE TOWN, SARGODHA 15 10-48-01760-4-049 AYESHA AKRAM M. -

Supreme Court of Pakistan Daimer Basha and Mohmand Dam Fund
SUPREME COURT OF PAKISTAN DAIMER BASHA AND MOHMAND DAM FUND ACCOUNT LIST OF DONOR FOR 03 SEP-18 RECEIPT Bank Depositor Name Amount AL BARAKA BANK (PAKISTAN) LTD MUHAMMAD YASIN 110 AL BARAKA BANK (PAKISTAN) LTD MUSTAFA NAEEM 200 AL BARAKA BANK (PAKISTAN) LTD NUZHAT KHILJI 360 AL BARAKA BANK (PAKISTAN) LTD RAFEEQ 500 AL BARAKA BANK (PAKISTAN) LTD RAHAT IQBAL 500 AL BARAKA BANK (PAKISTAN) LTD MUHAMMAD IKRAM 1,000 AL BARAKA BANK (PAKISTAN) LTD TARIQ RIAZ 1,000 AL BARAKA BANK (PAKISTAN) LTD SAJJAD AHMED 1,000 AL BARAKA BANK (PAKISTAN) LTD KHALID SHAH 1,000 AL BARAKA BANK (PAKISTAN) LTD SHAHZAIB 1,000 AL BARAKA BANK (PAKISTAN) LTD FAROOQ MALIK 1,000 AL BARAKA BANK (PAKISTAN) LTD ADC 1,000 AL BARAKA BANK (PAKISTAN) LTD AHSAN AHMED 1,000 AL BARAKA BANK (PAKISTAN) LTD NOOR UL AMIN 1,500 AL BARAKA BANK (PAKISTAN) LTD SHABBER AHMED 2,000 AL BARAKA BANK (PAKISTAN) LTD JAVED KHAN 10,000 AL BARAKA BANK (PAKISTAN) LTD JIBRAN 10,000 AL BARAKA BANK (PAKISTAN) LTD ZULFIQAR ALI 10,000 AL BARAKA BANK (PAKISTAN) LTD MUHAMMAD ZAHID 10,000 AL BARAKA BANK (PAKISTAN) LTD NAVEED KHAN 10,000 AL BARAKA BANK (PAKISTAN) LTD MUHAMMAD NASIR 20,000 AL BARAKA BANK (PAKISTAN) LTD NAJAM KHAN 20,000 AL BARAKA BANK (PAKISTAN) LTD FARMA ALI 38,000 AL BARAKA BANK (PAKISTAN) LTD ADC 100,000 AL BARAKA BANK (PAKISTAN) LTD WAHEEDA PARVEEN 300,000 AL BARAKA BANK (PAKISTAN) LTD Total 541,170 Allied Bank Limited ZEESHAN JEELANI 5 Allied Bank Limited GUL SHAIR 10 Allied Bank Limited ABDUL BASIT BAIG 10 Allied Bank Limited MUHAMMAD BILAL 10 Allied Bank Limited MUHAMMAD AZHAR 13 Allied -

Institute of Business Administration, Karachi
FINAL RESULT ‐ FALL 2018, ROUND 2 Announced on Monday, July, 16, 2018 INSTITUTE OF BUSINESS ADMINISTRATION, KARACHI BBA, BS (ACCOUNTING & FINANCE), BS (ECONOMICS) & BS (SOCIAL SCIENCES) ADMISSIONS TEST HELD ON SUNDAY, JULY 1, 2018 (FALL 2018, ROUND 2) LIST OF SUCCESSFUL CANDIDATES FOR DIRECT ADMISSION (BBA PROGRAM) SAT Test Math Eng Reading Analysis Writing Maximum Marks 800 800 8 8 8 Cut-Off Marks 650 640 Cumulative 18 Math Eng Total Eng Total IBA Test MCQ MCQ MCQ Essay ALL Maximum Marks 176 180 356 20 376 Cut-Off Marks 92 92 204 7 234 Seat S. No. App No. Name Father's Name No. 1 1032 5387 SYEDA ZARAH BATOOL NADEEM ISMAT 112 140 252 11.5 263.5 2 1047 5485 JAVERIA HASAN SYED ARIF‐UL‐HASAN 112 116 228 14.5 242.5 3 1073 5602 SAMEER DERO AKBAR DERO 104 124 228 13.5 241.5 4 1074 5604 HASSAN KHAN MOOSA KALEEM KHAN MOOSA 108 124 232 11 243 5 1093 5657 HUZAIFA AHMED KHATRI FEROZ AHMED KHATRI 124 100 224 14 238 6 1116 5736 UKASHA WASEEM WASEEM SULTAN 136 120 256 13 269 7 1139 5845 MUHAMMAD IRTIZA SYED MUHAMMAD KAUSAR MEHDI 96 132 228 16 244 8 1141 5852 MUHAMMAD MUSTAFA KHAN MUHAMMAD TAHA 120 108 228 13.5 241.5 9 1149 5902 TAIMOUR ARSHAD ARSHAD RAZZAQ 100 124 224 11.5 235.5 10 1163 5580 UROOJ FATIMA MUKHTIAR AHMED 100 124 224 10.5 234.5 11 1200 6028 KHAWAJA TALHA BIN AAMIR KHAWAJA AAMIR JALIL 116 136 252 12 264 12 1202 6032 MUHAMMAD TAHA KHAN IBRAT ULLAH KHAN 128 120 248 8 256 13 1237 6172 ANUSHA SHAMS SHAHAB SHAMS 92 148 240 14.5 254.5 14 1257 6249 SYEDA RABIYA ZAKI SYED ZAKI UR REHMAN 124 116 240 14.5 254.5 15 1272 6301 FAIZA FARRUKH FARRUKH