DOCSLIB.ORG

A Strong Triangle Inequality in Hyperbolic Geometry

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Strong Triangle Inequality in Hyperbolic Geometry Forum Geometricorum Volume 16 (2016) 99–114. FORUM GEOM ISSN 1534-1178 A Strong Triangle Inequality in Hyperbolic Geometry Csaba Biro´ and Robert C. Powers Abstract. For a triangle in the hyperbolic plane, let α, β, γ denote the angles opposite the sides a, b, c, respectively. Also, let h be the height of the altitude to side c. Under the assumption that α, β, γ can be chosen uniformly in the interval (0,π) and it is given that α + β + γ<π, we show that the strong triangle inequality a + b>c+ h holds approximately 79% of the time. To accomplish this, we prove a number of theoretical results to make sure that the probability can be computed to an arbitrary precision, and the error can be bounded. 1. Introduction It is well known that the Euclidean and hyperbolic planes satisfy the triangle inequality. What is less known is that in many cases a stronger triangle inequality holds. Specifically, a + b>c+ h (1) where a, b, c are the lengths of the three sides of the triangle and h is the height of the altitude to side c. We refer to inequality (1) as the strong triangle inequality and note that this inequality depends on which side of the triangle is labeled c. The strong triangle inequality was first introduced for the Euclidean plane by Bailey and Bannister in [1]. They proved, see also Klamkin [4], that inequality (1) 24 holds for all Euclidean triangles if γ<arctan 7 where γ is the angle opposite side c. Bailey and Bannister also showed that a + b = c + h for any Euclidean γ =arctan 24 γ isosceles triangle such that 7 and is the unique largest angle of the 24 triangle. We let B =arctan 7 and refer to B as the Bailey-Bannister bound. In 2007, Baker and Powers [2] showed that the strong triangle inequality holds for any hyperbolic triangle if γ ≤ Γ where Γ is the unique root of the function γ f(γ)=−1 − cos γ +sinγ +sin sin γ 2 π ◦ ◦ in the interval [0, 2 ]. It turns out that B ≈ 74 and Γ ≈ 66 leading to roughly an 8◦ difference between the Euclidean and hyperbolic bounds. It appears that the strong triangle inequality holds more often in the Euclidean plane than in the hyperbolic plane. Let α and β denote the angles opposite the sides a and b, respectively. Under the assumption that the angles α and β can be chosen uniformly in the interval (0,π) and α + β<π,Fa˘ıziev et al. [3] showed the strong triangle inequality holds in the Publication Date: April 1, 2016. Communicating Editor: Paul Yiu. 100 C. Biro´ and R. C. Powers γ a b h c α β Figure 1. A hyperbolic triangle Euclidean plane approximately 69% of the time. In addition, they asked how this percentage will change when working with triangles in the hyperbolic plane. In this paper, we answer this question by showing that the strong triangle inequality holds approximately 79% of the time. Moreover, we show that the stated probability can be computed to an arbitrary precision and that the error can be bounded. Unless otherwise noted, all geometric notions in this paper are on the hyper- bolic plane. Since our problem is invariant under scaling, we will assume that the Gaussian curvature of the plane is −1. We will use the notations a, b, c, h, α, β, γ for sides, height, and angles of a given triangle. (See Figure 1.) We will exten- sively use hyperbolic trigonometric formulas such as the law of sines and the two versions of the law of cosines. We refer the reader to Chapter 8 in [5] for a list of these various formulas. 2. Simple observations In this section we mention a few simple, but important observations about the main question. Proposition 1. If γ is not the unique greatest angle in a triangle, then the strong triangle inequality holds. Proof. Suppose that γ is not the greatest angle, say, α ≥ γ. Then a ≥ c,so a + b ≥ c + b ≥ c + h. Equality could only hold, if α = γ = π/2, which is impossible. Proposition 2. If γ ≥ π/2, then the strong triangle inequality does not hold. We will start with a lemma that is interesting in its own right. Lemma 3. In every triangle the following equation holds. sinh c sinh h =sinha sinh b sin γ Note that in Euclidean geometry the analogous theorem would be the statement that ch = ab sin γ, which is true by the fact that both sides of the equation represent twice the area of the triangle. Interestingly, in hyperbolic geometry, the sides of the corresponding equation do not represent the area of the triangle. A strong triangle inequality in hyperbolic geometry 101 Proof. By the law of sines, sinh b sinh c = , sin β sin γ so sinh b sin γ sinh c = . sin β By right triangle trigonometry, sinh h =sinha sin β. Multiplying these equations, the result follows. Proof of Proposition 2. Note that a + b>c+ h if and only if cosh(a + b) > cosh(c + h). Using the addition formula for cosh, then the fact that cosh h ≥ 1 and cosh c ≥ 0, and then the law of cosines, in this order, we get cos(c + h)= coshc cosh h +sinhc sinh h ≥ cosh c +sinhc sinh h = cosh a cosh b − sinh a sinh b cos γ +sinha sinh b sin γ = cosh a cosh b +sinha sinh b(sin γ − cos γ) Notice that sin γ − cos γ ≥ 1 if π/2 ≤ γ ≤ π.So cosh a cosh b +sinha sinh b(sin γ − cos γ) ≥ cosh a cosh b +sinha sinh b =cosh(a + b). 3. Converting angles to lengths Since the angles of a hyperbolic triangle uniquely determine the triangle, it is possible to rephrase the condition a + b>c+ h with α, β, γ. In what follows, our goal is find a function f(α, β, γ), as simple as possible, such that a + b>c+ h if and only if f(α, β, γ) > 0. Following Proposition 1 and Proposition 2, in the rest of the section we will assume that γ<π/2 is the greatest angle of the triangle. The following lemma is implicit in [2]. We include the proof for completeness. Lemma 4. A triangle satisfies the strong triangle inequality if and only if cos α cos β +cosγ − 1 < cosh h. cos γ +1− sin γ Furthermore, the formula holds with equality if and only if a + b = c + h. Proof. Recall that a + b>c+ h if and only if cosh(a + b) − cosh(c + h) > 0. Using the cosh addition formula and the law of cosines on cosh c,wehave cosh(a + b) − cosh(c + h) = cosh a cosh b +sinha sinh b − cosh c cosh h − sinh c sinh h = cosh c +sinha sinh b cos γ +sinha sinh b − cosh c cosh h − sinh c sinh h = cosh c(1 − cosh h)+sinha sinh b(cos γ +1)− sinh c sinh h 102 C. Biro´ and R. C. Powers By Lemma 3, cosh c(1 − cosh h)+sinha sinh b(cos γ +1)− sinh c sinh h = cosh c(1 − cosh h)+sinha sinh b(cos γ +1)− sinh a sinh b sin γ sinh a sinh b 1 − cosh2 h = cosh c +(1+coshh)(cos γ +1− sin γ) 1+coshh sinh a sinh b By the fact that sinh h =sinhb sin α =sinha sin β,wehave 1 − cosh2 h − sinh2 h − sinh b sin α · sinh a sin β = = = − sin α sin β, sinh a sinh b sinh a sinh b sinh a sinh b so, using the dual form of the law of cosines, cos(a + b) − cosh(c + h) sinh a sinh b = [− cosh c sin α sin β +(1+coshh)(cos γ +1− sin γ)] 1+coshh sinh a sinh b = [−(cos α cos β +cosγ) + (1 + cosh h)(cos γ +1− sin γ)] . 1+coshh sinh a sinh b Since 1+cosh h > 0, we have the strong triangle inequality holds, if and only if cos α cos β +cosγ<(1 + cosh h)(cos γ +1− sin γ), and the result follows. A minor variation of the proof shows the case of equality. Lemma 5. For all triangles with γ>max{α, β}, cos α cos β +cosγ > 1. cos γ +1− sin γ Proof. Without loss of generality, 0 <α≤ β<γ<π/2. Then 0 > sin γ(sin γ − 1) = sin2 γ − sin γ>sin2 β − sin γ cos2 β>cos2 β +sin2 β − sin γ =1− sin γ cos2 β +cosγ>1 − sin γ +cosγ, so cos2 β +cosγ > 1. 1 − sin γ +cosγ Since 0 < cos β ≤ cos α,wehave cos2 β +cosγ cos α cos β +cosγ ≤ , 1 − sin γ +cosγ 1 − sin γ +cosγ and the results follows. By Lemma 4 and Lemma 5, we can conclude that the strong triangle inequality holds if and only if cos α cos β +cosγ 2 − 1 < cosh2 h. cos γ +1− sin γ (2) A strong triangle inequality in hyperbolic geometry 103 Using the law of cosines, cosh2 h ==sinh2 h +1=sin2 β sinh2 a +1=sin2 β(cosh2 a − 1) + 1 cos β cos γ +cosα 2 =sin2 β − sin2 β +1 sin β sin γ cos β cos γ +cosα 2 =cos2 β + . sin γ (3) Equations (2) and (3) together imply the following statement.
Load more

Recommended publications
  • Inner Product Spaces Isaiah Lankham, Bruno Nachtergaele, Anne Schilling (March 2, 2007)
    MAT067 University of California, Davis Winter 2007 Inner Product Spaces Isaiah Lankham, Bruno Nachtergaele, Anne Schilling (March 2, 2007) The abstract definition of vector spaces only takes into account algebraic properties for the addition and scalar multiplication of vectors. For vectors in Rn, for example, we also have geometric intuition which involves the length of vectors or angles between vectors. In this section we discuss inner product spaces, which are vector spaces with an inner product defined on them, which allow us to introduce the notion of length (or norm) of vectors and concepts such as orthogonality. 1 Inner product In this section V is a finite-dimensional, nonzero vector space over F. Definition 1. An inner product on V is a map ·, · : V × V → F (u, v) →u, v with the following properties: 1. Linearity in first slot: u + v, w = u, w + v, w for all u, v, w ∈ V and au, v = au, v; 2. Positivity: v, v≥0 for all v ∈ V ; 3. Positive definiteness: v, v =0ifandonlyifv =0; 4. Conjugate symmetry: u, v = v, u for all u, v ∈ V . Remark 1. Recall that every real number x ∈ R equals its complex conjugate. Hence for real vector spaces the condition about conjugate symmetry becomes symmetry. Definition 2. An inner product space is a vector space over F together with an inner product ·, ·. Copyright c 2007 by the authors. These lecture notes may be reproduced in their entirety for non- commercial purposes. 2NORMS 2 Example 1. V = Fn n u =(u1,...,un),v =(v1,...,vn) ∈ F Then n u, v = uivi.
    [Show full text]
  • 5-7 the Pythagorean Theorem 5-7 the Pythagorean Theorem
    55-7-7 TheThe Pythagorean Pythagorean Theorem Theorem Warm Up Lesson Presentation Lesson Quiz HoltHolt McDougal Geometry Geometry 5-7 The Pythagorean Theorem Warm Up Classify each triangle by its angle measures. 1. 2. acute right 3. Simplify 12 4. If a = 6, b = 7, and c = 12, find a2 + b2 2 and find c . Which value is greater? 2 85; 144; c Holt McDougal Geometry 5-7 The Pythagorean Theorem Objectives Use the Pythagorean Theorem and its converse to solve problems. Use Pythagorean inequalities to classify triangles. Holt McDougal Geometry 5-7 The Pythagorean Theorem Vocabulary Pythagorean triple Holt McDougal Geometry 5-7 The Pythagorean Theorem The Pythagorean Theorem is probably the most famous mathematical relationship. As you learned in Lesson 1-6, it states that in a right triangle, the sum of the squares of the lengths of the legs equals the square of the length of the hypotenuse. a2 + b2 = c2 Holt McDougal Geometry 5-7 The Pythagorean Theorem Example 1A: Using the Pythagorean Theorem Find the value of x. Give your answer in simplest radical form. a2 + b2 = c2 Pythagorean Theorem 22 + 62 = x2 Substitute 2 for a, 6 for b, and x for c. 40 = x2 Simplify. Find the positive square root. Simplify the radical. Holt McDougal Geometry 5-7 The Pythagorean Theorem Example 1B: Using the Pythagorean Theorem Find the value of x. Give your answer in simplest radical form. a2 + b2 = c2 Pythagorean Theorem (x – 2)2 + 42 = x2 Substitute x – 2 for a, 4 for b, and x for c. x2 – 4x + 4 + 16 = x2 Multiply.
    [Show full text]
  • Geometry ­ Ch 5 ­ Exterior Angles & Triangle Inequality December 01, 2014
    Geometry ­ Ch 5 ­ Exterior Angles & Triangle Inequality December 01, 2014 The “Three Possibilities” Property: either a>b, a=b, or a<b The Transitive Property: If a>b and b>c, then a>c The Addition Property: If a>b, then a+c>b+c The Subtraction Property: If a>b, then a‐c>b‐c The Multiplication Property: If a>b and c>0, then ac>bc The Division Property: If a>b and c>0, then a/c>b/c The Addition Theorem of Inequality: If a>b and c>d, then a+c>b+d The “Whole Greater than Part” Theorem: If a>0, b>0, and a+b=c, then c>a and c>b Def: An exterior angle of a triangle is an angle that forms a linear pair with an angle of the triangle. A In ∆ABC, exterior ∠2 forms a linear pair with ∠ACB. The other two angles of the triangle, ∠1 (∠B) and ∠A are called remote interior angles with respect to ∠2. 1 2 B C Theorem 12: The Exterior Angle Theorem An Exterior angle of a triangle is greater than either remote interior angle. Find each of the following sums. 3 4 26. ∠1+∠2+∠3+∠4 2 1 6 7 5 8 27. ∠1+∠2+∠3+∠4+∠5+∠6+∠7+ 9 12 ∠8+∠9+∠10+∠11+∠12 11 10 28. ∠1+∠5+∠9 31. What does the result in exercise 30 indicate about the sum of the exterior 29. ∠3+∠7+∠11 angles of a triangle? 30. ∠2+∠4+∠6+∠8+∠10+∠12 1 Geometry ­ Ch 5 ­ Exterior Angles & Triangle Inequality December 01, 2014 After proving the Exterior Angle Theorem, Euclid proved that, in any triangle, the sum of any two angles is less than 180°.
    [Show full text]
  • Indirect Proof and Inequalities in One Triangle
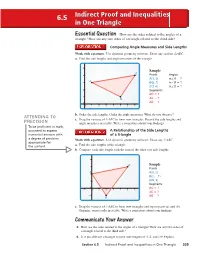
    6.5 Indirect Proof and Inequalities in One Triangle EEssentialssential QQuestionuestion How are the sides related to the angles of a triangle? How are any two sides of a triangle related to the third side? Comparing Angle Measures and Side Lengths Work with a partner. Use dynamic geometry software. Draw any scalene △ABC. a. Find the side lengths and angle measures of the triangle. 5 Sample C 4 Points Angles A(1, 3) m∠A = ? A 3 B(5, 1) m∠B = ? C(7, 4) m∠C = ? 2 Segments BC = ? 1 B AC = ? AB = 0 ? 01 2 34567 b. Order the side lengths. Order the angle measures. What do you observe? ATTENDING TO c. Drag the vertices of △ABC to form new triangles. Record the side lengths and PRECISION angle measures in a table. Write a conjecture about your fi ndings. To be profi cient in math, you need to express A Relationship of the Side Lengths numerical answers with of a Triangle a degree of precision Work with a partner. Use dynamic geometry software. Draw any △ABC. appropriate for the content. a. Find the side lengths of the triangle. b. Compare each side length with the sum of the other two side lengths. 4 C Sample 3 Points A A(0, 2) 2 B(2, −1) C 1 (5, 3) Segments 0 BC = ? −1 01 2 3456 AC = ? −1 AB = B ? c. Drag the vertices of △ABC to form new triangles and repeat parts (a) and (b). Organize your results in a table. Write a conjecture about your fi ndings.
    [Show full text]
  • CS261 - Optimization Paradigms Lecture Notes for 2013-2014 Academic Year
    CS261 - Optimization Paradigms Lecture Notes for 2013-2014 Academic Year ⃝c Serge Plotkin January 2014 1 Contents 1 Steiner Tree Approximation Algorithm 6 2 The Traveling Salesman Problem 10 2.1 General TSP . 10 2.1.1 Definitions . 10 2.1.2 Example of a TSP . 10 2.1.3 Computational Complexity of General TSP . 11 2.1.4 Approximation Methods of General TSP? . 11 2.2 TSP with triangle inequality . 12 2.2.1 Computational Complexity of TSP with Triangle Inequality . 12 2.2.2 Approximation Methods for TSP with Triangle Inequality . 13 3 Matchings, Edge Covers, Node Covers, and Independent Sets 22 3.1 Minumum Edge Cover and Maximum Matching . 22 3.2 Maximum Independent Set and Minimum Node Cover . 24 3.3 Minimum Node Cover Approximation . 24 4 Intro to Linear Programming 27 4.1 Overview . 27 4.2 Transformations . 27 4.3 Geometric interpretation of LP . 29 4.4 Existence of optimum at a vertex of the polytope . 30 4.5 Primal and Dual . 32 4.6 Geometric view of Linear Programming duality in two dimensions . 33 4.7 Historical comments . 35 5 Approximating Weighted Node Cover 37 5.1 Overview and definitions . 37 5.2 Min Weight Node Cover as an Integer Program . 37 5.3 Relaxing the Linear Program . 37 2 5.4 Primal/Dual Approach . 38 5.5 Summary . 40 6 Approximating Set Cover 41 6.1 Solving Minimum Set Cover . 41 7 Randomized Algorithms 46 7.1 Maximum Weight Crossing Edge Set . 46 7.2 The Wire Routing Problem . 48 7.2.1 Overview .
    [Show full text]
  • Use the Converse of the Pythagorean Theorem
    Use the Converse of the Pythagorean Theorem Goal • Use the Converse of the Pythagorean Theorem to determine if a triangle is a right triangle. Your Notes THEOREM 7.2: CONVERSE OF THE PYTHAGOREAN THEOREM If the square of the length of the longest side of a triangle is equal aI to the sum of the squares of the c A lengths of the other two sides, then the triangle is a triangle. If c2 = a 2 + b2, then AABC is a triangle. Verify right triangles Tell whether the given triangle is a right triangle. a. b. 24 6 9 Solution Let c represent the length of the longest side of the triangle. Check to see whether the side lengths satisfy the equation c 2 = a 2 + b 2. a. ( )2 ? 2 + 2 • The triangle a right triangle. b. 2? 2 + 2 The triangle a right triangle. 174 Lesson 7.2 • Geometry Notetaking Guide Copyright @ McDougal Littell/Houghton Mifflin Company. Your Notes THEOREM 7.3 A If the square of the length of the longest b c side of a triangle is less than the sum of B the squares of the lengths of the other C a two sides, then the triangle ABC is an triangle. If c 2 < a 2 + b2 , then the triangle ABC is THEOREM 7.4 A If the square of the length of the longest bN side of a triangle is greater than the sum of C B the squares of the lengths of the other two a sides, then the triangle ABC is an triangle.
    [Show full text]
  • Inequalities for C-S Seminorms and Lieb Functions
    CORE Metadata, citation and similar papers at core.ac.uk Provided by Elsevier - Publisher Connector LINEAR ALGEBRA AND ITS APPLiCATIONS ELSEVIER Linear Algebra and its Applications 291 (1999) 103-113 - Inequalities for C-S seminorms and Lieb functions Roger A. Horn a,., Xingzhi Zhan b.l ;1 Department (?(Mathematics, Uni('('rsify of Utah, Salt L(lke CifY, UT 84103. USA h Institute of Mathematics. Pekins; University, Beijing 10087J. People's Republic of C/WICt Received 3 July 1998: accepted 3 November 1998 Submitted by R. Bhatia Abstract Let AI" be the space of 1/ x 11 complex matrices. A seminorm /I ." on NI" is said to be a C-S seminorm if IIA-AII = IIAA"II for all A E Mil and IIAII ~ IIBII whenever A, B, and B-A are positive semidefinite. If II . II is any nontrivial C-S seminorm on AI", we show that 111/'111 is a unitarily invariant norm on M,n which permits many known inequalities for unitarily invariant norms to be generalized to the setting of C-S seminorrns, We prove a new inequality for C-S seminorms that includes as special cases inequalities of Bhatia et al., for unitarily invariant norms. Finally. we observe that every C-S seminorm belongs to the larger class of Lieb functions, and we prove some new inequalities for this larger class. © 1999 Elsevier Science Inc. All rights reserved. 1. Introduction Let M" be the space of 11 x Jl complex matrices and denote the matrix ab­ solute value of any A E M" by IA I=(A* A)1/2.
    [Show full text]
  • Simplex-Tree Based Kinematics of Foldable Objects As Multi-Body Systems Involving Loops
    Simplex-Tree Based Kinematics of Foldable Objects as Multi-body Systems Involving Loops Li Han and Lee Rudolph Department of Mathematics and Computer Science Clark University, Worcester, MA 01610 Email: [email protected], [email protected] Abstract— Many practical multi-body systems involve loops. Smooth manifolds are characterized by the existence of local Studying the kinematics of such systems has been challenging, coordinates, but although some manifolds are equipped with partly because of the requirement of maintaining loop closure global coordinates (like the joint angle parameters, in the constraints, which have conventionally been formulated as highly nonlinear equations in joint parameters. Recently, novel para- cases of a serial chain without closure constraints or [7, 8] a meters defined by trees of triangles have been introduced for a planar loop satisfying the technical “3 long links” condition), broad class of linkage systems involving loops (e.g., spatial loops typically a manifold has neither global coordinates nor any with spherical joints and planar loops with revolute joints); these standard atlas of local coordinate charts. Thus, calculations parameters greatly simplify kinematics related computations that depend on coordinates are often difficult to perform. and endow system configuration spaces with highly tractable piecewise convex geometries. In this paper, we describe a more Some recent kinematic work uses new parameters that are general approach for multi-body systems, with loops, that allow not conventional joint parameters. One series of papers [9, construction trees of simplices. We illustrate the applicability and 10, 11, 12, 13] presented novel formulations and techniques, efficiency of our simplex-tree based approach to kinematics by a including distance geometry, linear programming and flag study of foldable objects.
    [Show full text]
  • Find X. 9. SOLUTION: in a Right Triangle, the Sum of the Squares Of
    8-2 The Pythagorean Theorem and Its Converse Find x. 9. SOLUTION: In a right triangle, the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse. The length of the hypotenuse is x and the lengths of the legs are 12 and 16. 10. SOLUTION: In a right triangle, the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse. The length of the hypotenuse is 15 and the lengths of the legs are 9 and x. eSolutions11. Manual - Powered by Cognero Page 1 SOLUTION: In a right triangle, the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse. The length of the hypotenuse is 5 and the lengths of the legs are 2 and x. 12. SOLUTION: In a right triangle, the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse. The length of the hypotenuse is 66 and the lengths of the legs are 33 and x. 13. SOLUTION: In a right triangle, the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse. The length of the hypotenuse is x and the lengths of the legs are . 14. SOLUTION: In a right triangle, the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse.
    [Show full text]
  • MATH32052 Hyperbolic Geometry
    MATH32052 Hyperbolic Geometry Charles Walkden 12th January, 2019 MATH32052 Contents Contents 0 Preliminaries 3 1 Where we are going 6 2 Length and distance in hyperbolic geometry 13 3 Circles and lines, M¨obius transformations 18 4 M¨obius transformations and geodesics in H 23 5 More on the geodesics in H 26 6 The Poincar´edisc model 39 7 The Gauss-Bonnet Theorem 44 8 Hyperbolic triangles 52 9 Fixed points of M¨obius transformations 56 10 Classifying M¨obius transformations: conjugacy, trace, and applications to parabolic transformations 59 11 Classifying M¨obius transformations: hyperbolic and elliptic transforma- tions 62 12 Fuchsian groups 66 13 Fundamental domains 71 14 Dirichlet polygons: the construction 75 15 Dirichlet polygons: examples 79 16 Side-pairing transformations 84 17 Elliptic cycles 87 18 Generators and relations 92 19 Poincar´e’s Theorem: the case of no boundary vertices 97 20 Poincar´e’s Theorem: the case of boundary vertices 102 c The University of Manchester 1 MATH32052 Contents 21 The signature of a Fuchsian group 109 22 Existence of a Fuchsian group with a given signature 117 23 Where we could go next 123 24 All of the exercises 126 25 Solutions 138 c The University of Manchester 2 MATH32052 0. Preliminaries 0. Preliminaries 0.1 Contact details § The lecturer is Dr Charles Walkden, Room 2.241, Tel: 0161 27 55805, Email: [email protected]. My office hour is: WHEN?. If you want to see me at another time then please email me first to arrange a mutually convenient time. 0.2 Course structure § 0.2.1 MATH32052 § MATH32052 Hyperbolic Geoemtry is a 10 credit course.
    [Show full text]
  • The Euler Line in Hyperbolic Geometry
    The Euler Line in Hyperbolic Geometry Jeffrey R. Klus Abstract- In Euclidean geometry, the most commonly known system of geometry, a very interesting property has been proven to be common among all triangles. For every triangle, there exists a line that contains three major points of concurrence for that triangle: the centroid, orthocenter, and circumcenter. The centroid is the concurrence point for the three medians of the triangle. The orthocenter is the concurrence point of the altitudes. The circumcenter is the point of concurrence of the perpendicular bisectors of each side of the triangle. This line that contains these three points is called the Euler line. This paper discusses whether or not the Euler line exists in Hyperbolic geometry, an alternate system of geometry. The Poincare Disc Model for Hyperbolic geometry, together with Geometer’s Sketchpad software package was used extensively to answer this question. Introduction In Euclidean geometry, the most Second, for any circle that is orthogonal commonly known system of geometry, a to the unit circle, the points on that circle very interesting property has been lying in the interior of the unit circle will proven to be common among all be considered a hyperbolic line triangles. For every triangle, there exists (Wallace, 1998, p. 336). a line that contains three major points of concurrence for that triangle: the Methods centroid, orthocenter, and circumcenter. Locating the Centroid The centroid is the concurrence point for In attempting to locate the Euler line, the the three medians of the triangle. The first thing that needs to be found is the orthocenter is the concurrence point of midpoint of each side of the hyperbolic the altitudes.
    [Show full text]
  • DIY Hyperbolic Geometry
    DIY hyperbolic geometry Kathryn Mann written for Mathcamp 2015 Abstract and guide to the reader: This is a set of notes from a 5-day Do-It-Yourself (or perhaps Discover-It-Yourself) intro- duction to hyperbolic geometry. Everything from geodesics to Gauss-Bonnet, starting with a combinatorial/polyhedral approach that assumes no knowledge of differential geometry. Al- though these are set up as \Day 1" through \Day 5", there is certainly enough material hinted at here to make a five week course. In any case, one should be sure to leave ample room for play and discovery before moving from one section to the next. Most importantly, these notes were meant to be acted upon: if you're reading this without building, drawing, and exploring, you're doing it wrong! Feedback: As often happens, these notes were typed out rather more hastily than I intended! I would be quite happy to hear suggestions/comments and know about typos or omissions. For the moment, you can reach me at [email protected] As some of the figures in this work are pulled from published work (remember, this is just a class handout!), please only use and distribute as you would do so with your own class mate- rials. Day 1: Wrinkly paper If we glue equilateral triangles together, 6 around a vertex, and keep going forever, we build a flat (Euclidean) plane. This space is called E2. Gluing 5 around a vertex eventually closes up and gives an icosahedron, which I would like you to think of as a polyhedral approximation of a round sphere.
    [Show full text]