Relative Magnitudes of Sources of Uncertainty in Assessing Climate Change Impacts on Water Supply Security for the Southern Adel
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Hillslope Erosion and Post-Fire Sediment Trapping at Mount Bold, South Australia
42 Wildfire and Water Quality: Processes, Impacts and Challenges (Proceedings of a conference held in Banff, Canada, 11–14 June 2012) (IAHS Publ. 354, 2012). Hillslope erosion and post-fire sediment trapping at Mount Bold, South Australia ROWENA MORRIS1,2, DEIRDRE DRAGOVICH3 & BERTRAM OSTENDORF1 1 Earth and Environmental Science, PMB 1, Glen Osmond, University of Adelaide, South Australia 5064, Australia [email protected] 2 Bushfire Cooperative Research Centre, Level 5, 340 Albert Street, East Melbourne, Victoria 3002, Australia 3 School of Geosciences, Madsen Building (F09), University of Sydney, New South Wales 2006, Australia Abstract Successful placement of sediment traps requires an understanding of how hillslope morphology influences erosion. Following the 2007 Mount Bold wildfire, in South Australia, a 1 in 5 year rainfall event resulted in the failure of many sediment traps due to substantial sediment movement within the reservoir reserve. This study assesses how hillslope morphology can influence post-fire surface erosion and the subsequent appropriate placement of sediment traps. Erosion pins and sediment traps were used at five different sites to measure hillslope surface change and trapped sediment volumes. Terrestrial laser scanning was used to model surface change where slope gradients are 1:2 or greater. Surface change was assessed in relation to slope gradient, slope length, cross-slope curvature, hillslope position and fire severity. The results suggested a threshold for substantial increased sediment yield at slope gradients of 1:2. The findings also suggested that concave cross-slope curvatures were associated with significantly larger amounts of sediment movement. Key words water reservoir; sediment trap; erosion pins; terrestrial laser scanning; slope gradient; cross-slope plan curvature, South Australia INTRODUCTION Wildfires influence soil surface processes resulting in the potential for increased sedimentation of reservoirs and impacts on water quality (Smith et al., 2011). -

Photography by John Hodgson Foreword By
Editor in chief Christopher B. Daniels Foreword by Photography by John Hodgson Barbara Hardy Table of contents Foreword by Barbara Hardy 13 Preface and acknowledgements 14 CHAPTER 1 Introduction 35 Box 1: The watercycle Philip Roetman 38 Box 2: The four colours of freshwater Jennifer McKay 44 Box 3: Environmentally sustainable development (ESD) Jennifer McKay 46 Box 4: Sustainable development timeline Jennifer McKay 47 Box 5: Adelaide’s water supply timeline Thorsten Mosisch 48 CHAPTER 2 The variable climate 51 Elizabeth Curran, Christopher Wright, Darren Ray Box 6: Does Adelaide have a Mediterranean climate? Elizabeth Curran and Darren Ray 53 Box 7: The nature of flooding Robert Bourman 56 Box 8: Floods in the Adelaide region Chris Wright 61 Box 9: Significant droughts Elizabeth Curran 65 CHAPTER 3 Catchments and waterways 69 Robert P. Bourman, Nicholas Harvey, Simon Bryars Box 10: The biodiversity of Buckland Park Kate Smith 71 Box 11: Tulya Wodli Riparian Restoration Project Jock Conlon 77 Box 12: Challenges to environmental flows Peter Schultz 80 Box 13: The flood of 1931 David Jones 83 Box 14: Why conserve the Field River? Chris Daniels 87 CHAPTER 4 Aquifers and groundwater 91 Steve Barnett, Edward W. Banks, Andrew J. Love, Craig T. Simmons, Nabil Z. Gerges Box 15: Soil profiles and soil types in the Adelaide region Don Cameron 93 Box 16: Why do Adelaide houses crack in summer? Don Cameron 95 Box 17: Salt damp John Goldfinch 99 Box 18: Saltwater intrusion Ian Clark 101 CHAPTER 5 Biodiversity of the waterways 105 Christopher B. Daniels, -

ORNITHOLOGIST VOLUME 44 - PARTS 1&2 - November - 2019
SOUTH AUSTRALIAN ORNITHOLOGIST VOLUME 44 - PARTS 1&2 - November - 2019 Journal of The South Australian Ornithological Association Inc. In this issue: Variation in songs of the White-eared Honeyeater Phenotypic diversity in the Copperback Quailthrush and a third subspecies Neonicotinoid insecticides Bird Report, 2011-2015: Part 1, Non-passerines President: John Gitsham The South Australian Vice-Presidents: Ornithological John Hatch, Jeff Groves Association Inc. Secretary: Kate Buckley (Birds SA) Treasurer: John Spiers FOUNDED 1899 Journal Editor: Merilyn Browne Birds SA is the trading name of The South Australian Ornithological Association Inc. Editorial Board: Merilyn Browne, Graham Carpenter, John Hatch The principal aims of the Association are to promote the study and conservation of Australian birds, to disseminate the results Manuscripts to: of research into all aspects of bird life, and [email protected] to encourage bird watching as a leisure activity. SAOA subscriptions (e-publications only): Single member $45 The South Australian Ornithologist is supplied to Family $55 all members and subscribers, and is published Student member twice a year. In addition, a quarterly Newsletter (full time Student) $10 reports on the activities of the Association, Add $20 to each subscription for printed announces its programs and includes items of copies of the Journal and The Birder (Birds SA general interest. newsletter) Journal only: Meetings are held at 7.45 pm on the last Australia $35 Friday of each month (except December when Overseas AU$35 there is no meeting) in the Charles Hawker Conference Centre, Waite Road, Urrbrae (near SAOA Memberships: the Hartley Road roundabout). Meetings SAOA c/o South Australian Museum, feature presentations on topics of ornithological North Terrace, Adelaide interest. -

A Study of Changing Garden Styles and Practices in Post War Suburban
13' 1.qt I '; l- MITCHAM'S FRONT GARDENS I t- i' L I I I I I I A STUDY OF CHANGING GARDEN STYLES AND PRACTICES iI I IN POST WAR SUBURBAN ADEI,\IDE by Elizabeth Margaret Caldicott, B.A. A thesis submitted for the degree of Master of Arts in Geography University of Adelaide March 1994 TABLE OF CONTENTS Page TITLE PACE (i) TABLE OF CONTENTS (ii) LIST OF TABLES (ix) LIST OF MAPS (x) LIST OF FICURES (xi) LIST OF PIATES (xiii) ABSTRACT (xv) DECIARATION (xvii) ACKNOWLEDGMENTS (xviii) 1. INTRODUCTION 1 1.1 Background to and aims of the investigation 2 1.1.1 Part I - Ideas for garden studies 2 1.1.2 Part II - The detailed case study 7 1.2 lssues to be investigated 7 1.3 Mitcham City Council - the fieldwork case study area 8 PART I IDEAS FOR GARDEN STUDIES 2. Ideas for garden studies - a review of literature 11 2.1 Academic papers 11 2.2 Urban and environmental commentaries 18 2.3 Historians 19 2.4 Historical popular gardening literature 20 2.4.1 Early South Australian gardening guides 22 2.4.2 Specialist writers 24 2.4.3 Early works on Australian native flora 26 (i i) Page 2.5 Early Australian gardens 28 2.6 Towards an Australian garden ethos 30 2.7 Summary 36 3 A history of garden design to the present 37 3.1 Cardens in history 37 3.1.1 The ancient gardens 39 3.1.2 The Renaissance 40 3.1.3 The English garden tradition 41 3.1.4 Victoriana - the picturesque garden 42 3.1.5 North American gardens 43 3.1.6 Present day linl<s with the past 45 3.2 The Botanic Cardens of Adelaide 45 3.3 Modern Australian suburban gardens 47 3.3.1 Adelaide's early colonial gardens 49 3.3.2 1900-1945 gardens in Adelaide 50 3.3.3 Post World War ll gardens - 1945-1970 51 3.3.4 i 970s to the present 53 3.4 The cultivation of Australian native plants 54 3.5 The rise and demise of the 'all native' garden 56 3.6 Conclusions and Hypotheses 1 and 2 57 4. -

Summary of Groundwater Recharge Estimates for the Catchments of the Western Mount Lofty Ranges Prescribed Water Resources Area
TECHNICAL NOTE 2008/16 Department of Water, Land and Biodiversity Conservation SUMMARY OF GROUNDWATER RECHARGE ESTIMATES FOR THE CATCHMENTS OF THE WESTERN MOUNT LOFTY RANGES PRESCRIBED WATER RESOURCES AREA Graham Green and Dragana Zulfic November 2007 © Government of South Australia, through the Department of Water, Land and Biodiversity Conservation 2008 This work is Copyright. Apart from any use permitted under the Copyright Act 1968 (Cwlth), no part may be reproduced by any process without prior written permission obtained from the Department of Water, Land and Biodiversity Conservation. Requests and enquiries concerning reproduction and rights should be directed to the Chief Executive, Department of Water, Land and Biodiversity Conservation, GPO Box 2834, Adelaide SA 5001. Disclaimer The Department of Water, Land and Biodiversity Conservation and its employees do not warrant or make any representation regarding the use, or results of the use, of the information contained herein as regards to its correctness, accuracy, reliability, currency or otherwise. The Department of Water, Land and Biodiversity Conservation and its employees expressly disclaims all liability or responsibility to any person using the information or advice. Information contained in this document is correct at the time of writing. Information contained in this document is correct at the time of writing. ISBN 978-1-921218-81-1 Preferred way to cite this publication Green G & Zulfic D, 2008, Summary of groundwater recharge estimates for the catchments of the Western -

Fish Monitoring Across Regional Catchments of the Adelaide and Mount Lofty Ranges Region 2015–17
Fish monitoring across regional catchments of the Adelaide and Mount Lofty Ranges region 2015–17 David W. Schmarr, Rupert Mathwin and David L.M. Cheshire SARDI Publication No. F2018/000217-1 SARDI Research Report Series No. 990 SARDI Aquatics Sciences PO Box 120 Henley Beach SA 5022 August 2018 Schmarr, D. et al. (2018) Fish monitoring across regional catchments of the Adelaide and Mount Lofty Ranges region 2015–17 Fish monitoring across regional catchments of the Adelaide and Mount Lofty Ranges region 2015–17 Project David W. Schmarr, Rupert Mathwin and David L.M. Cheshire SARDI Publication No. F2018/000217-1 SARDI Research Report Series No. 990 August 2018 II Schmarr, D. et al. (2018) Fish monitoring across regional catchments of the Adelaide and Mount Lofty Ranges region 2015–17 This publication may be cited as: Schmarr, D.W., Mathwin, R. and Cheshire, D.L.M. (2018). Fish monitoring across regional catchments of the Adelaide and Mount Lofty Ranges region 2015-17. South Australian Research and Development Institute (Aquatic Sciences), Adelaide. SARDI Publication No. F2018/000217- 1. SARDI Research Report Series No. 990. 102pp. South Australian Research and Development Institute SARDI Aquatic Sciences 2 Hamra Avenue West Beach SA 5024 Telephone: (08) 8207 5400 Facsimile: (08) 8207 5415 http://www.pir.sa.gov.au/research DISCLAIMER The authors warrant that they have taken all reasonable care in producing this report. The report has been through the SARDI internal review process, and has been formally approved for release by the Research Chief, Aquatic Sciences. Although all reasonable efforts have been made to ensure quality, SARDI does not warrant that the information in this report is free from errors or omissions. -

Impacts of Climate Change on Surface Water in the Onkaparinga Catchment
Impacts of Climate Change on Surface Water in the Onkaparinga Catchment Final Report Volume 1: Hydrological Model Development and Sources of Uncertainty Westra, S., Thyer, M., Leonard, M., Kavetski, D. & Lambert, M. Goyder Institute for Water Research Technical Report Series No. 14/22 www.goyderinstitute.org Goyder Institute for Water Research Technical Report Series ISSN: 1839-2725 Impacts of Climate Change on Onkaparinga: Final Report 1 – Hydrological Model Development The Goyder Institute for Water Research is a partnership between the South Australian Government through the Department of Environment, Water and Natural Resources, CSIRO, Flinders University, the University of Adelaide and the University of South Australia. The Institute will enhance the South Australian Government’s capacity to develop and deliver science-based policy solutions in water management. It brings together the best scientists and researchers across Australia to provide expert and independent scientific advice to inform good government water policy and identify future threats and opportunities to water security. The following Associate organisations contributed to this report: Enquires should be addressed to: Goyder Institute for Water Research Level 1, Torrens Building 220 Victoria Square, Adelaide, SA, 5000 tel: 08-8303 8952 e-mail: [email protected] Citation Westra, S., Thyer, M., Leonard, M., Kavetski, D. & Lambert, M., 2014, Impacts of Climate Change on Surface Water in the Onkaparinga Catchment – Volume 1: Hydrological Model Development and Sources of Uncertainty, Goyder Institute for Water Research Technical Report Series No. 14/22, Adelaide, South Australia. Copyright © 2014 University of Adelaide. To the extent permitted by law, all rights are reserved and no part of this publication covered by copyright may be reproduced or copied in any form or by any means except with the written permission of the University of Adelaide. -

2019-20 Annual Report
2019-20 South Australian Water Corporation Annual Report FOR THE YEAR ENDING 30 JUNE 2020 FOR FURTHER DETAILS CONTACT SA Water Corporation ABN 69 336 525 019 Head office 250 Victoria Square/Tarntanyangga Adelaide SA 5000 Postal address GPO Box 1751 Adelaide SA 5001 Website sawater.com.au Please direct enquiries about this report to our Customer Care Centre on 1300 SA WATER (1300 729 283) or [email protected] ISSN: 1833-9980 0052R12009 28 September 2020 Letter of Transmittal 28 September 2020 The Honourable David Speirs Minister for Environment and Water Dear Minister On behalf of the Board of SA Water, I am pleased to present the Corporation’s Annual Report for the financial year ending 30 June 2020. The report is submitted for your information and presentation to Parliament, in accordance with requirements of the Public Corporations Act 1993 and the Public Sector Act 2009. This report is verified as accurate for the purposes of annual reporting to the Parliament of South Australia.. Andrew Fletcher AO Chair of the Board 3 SA Water 2019-20 Annual Report Contents A message from the Chair 5 Effective governance 56 A message from the Chief Executive 6 Legislation 56 Key regulators 56 About SA Water 8 The Board 56 Our vision 8 Directors’ interests and benefits 56 Our values 8 Board committees 56 Our organisation 8 Organisation structure 57 Our strategy 10 Financial performance 59 Financial performance summary 59 Our services 12 Contributions to government 60 Overview of our networks and assets 12 Capital Expenditure 60 Map of -
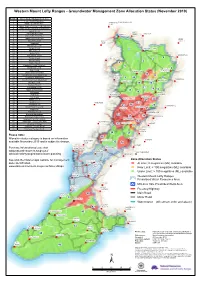
Groundwater Management Zone Allocation Status (November 2019)
Western Mount Lofty Ranges - Groundwater Management Zone Allocation Status (November 2019) Number Groundwater Management Zone 1 Lower South Para River KANGAROO") ROSEWORTHY 2 Middle SouthPara River FLAT 3 Upper South Para River (Adelaidean) ") 4 Upper South ParaRiver (Kanmantoo) 5 Gould Creek SANDY 6 Little Para Reservoir GAWLER CREEK LYNDOCH 7 Lower Little Para River ") ") ") 8 Upper Little Para River EDEN 9 Mount Pleasant ANGLE VALLEY 10 Birdwood VALE ") ") 11 Hannaford Creek 12 Angas Creek 1 WILLIAMSTOWN 13 Millers Creek ") 14 Gumeracha 15 McCormick Creek SPRINGTON 4 ") 16 Footes Creek ELIZABETH 3 17 Kenton Valley ") 2 18 Cudlee Creek 6 19 Kangaroo Creek Reservoir 5 20 Kersbrook Creek MOUNT 9 21 Sixth Creek 7 KERSBROOK PLEASANT ") 22 Charleston Kanmantoo ") Inverbrackie Creek Kanmantoo 13 23 TEA TREE 11 24 Charleston Adelaidean GULLY 8 20 10 TUNGKILLO 25 Inverbrackie Creek Adelaidean ") GUMERACHA ") BIRDWOOD HOUGHTON ") ") 26 Mitchell Creek ") 14 16 27 Western Branch 28 Lenswood Creek 17 15 29 Upper Onkaparinga 19 12 30 Balhannah 18 ") MOUNT 31 Hahndorf ROSTREVOR TORRENS 32 Cox Creek ") LOBETHAL CHERRYVILLE ") 22 33 Aldgate Creek ") 24 34 Scott Creek ADELAIDE 27 35 Chandlers Hill ") 21 28 23 HARROGATE 36 Mount Bold Reservoir WOODSIDE ") URAIDLA ") 25 37 Biggs Flat ") 38 Echunga Creek ") INVERBRACKIE 39 Myponga Adelaidean 32 40 Myponga Sedimentary 29 ") 26 BRUKUNGA ") 41 Hindmarsh Fractured Rock BALHANNAH 42 Hindmarsh Tiers Sedimentary BLACKWOOD 30 ") HAHNDORF NAIRNE 43 Fleurieu Permian 33 ") ") 44 Southern Fleurieu North 31 45 Southern Fleurieu South MOUNT BARKER 34 37 ") Please note: 35 Allocation status category is based on information ECHUNGA CLARENDON ") WISTOW MORPHETT ") ") available November 2019 and is subject to change. -

Fish Community and Flow Ecology in the Western Mount Lofty Ranges Environmental Water Provisions Trial Reaches
Fish Community and Flow Ecology in the Western Mount Lofty Ranges Environmental Water Provisions Trial Reaches Dale McNeil, David Schmarr, Phillipa Wilson and David Reid SARDI Publication No. F2011/000313-1 SARDI Research Report Series No. 581 October 2011 Fish Community and Flow Ecology in the Western Mount Lofty Ranges Environmental Water Provisions Trial Reaches Final Report to the Adelaide and Mount Lofty Ranges Natural Resources Management Board and the SA Department for Water. Dale McNeil, David Schmarr, Phillipa Wilson and David Reid SARDI Publication No. F2011/000313-1 SARDI Research Report Series No. 581 October 2011 FRONTISPIECE: Surveying Site Access above the South Para River Gorge. This Publication may be cited as: McNeil, D.G., Schmarr, D.W., Wilson, P.J. and Reid D. J (2011). Fish Community and Flow Ecology in the Western Mount Lofty Ranges Environmental Water Provisions Trial Reaches. Final Report to the Adelaide and Mount Lofty Ranges Natural Resources Management Board and the SA Department for Water. South Australian Research and Development Institute (Aquatic Sciences), Adelaide. SARDI Research Report Series No. 581. 238pp. South Australian Research and Development Institute SARDI Aquatic Sciences 2 Hamra Avenue West Beach SA 5024 Telephone: (08) 8207 5400 Facsimile: (08) 8207 5406 http://www.sardi.sa.gov.au DISCLAIMER The authors warrant that they have taken all reasonable care in producing this report. The report has been through the SARDI Aquatic Sciences internal review process, and has been formally approved for release by the Chief, Aquatic Sciences. Although all reasonable efforts have been made to ensure quality, SARDI Aquatic Sciences does not warrant that the information in this report is free from errors or omissions. -

South Australian Heritage Register
South Australian HERITAGE COUNCIL South Australian Heritage Register List of State Heritage Places in South Australia – as at 2 February 2021 SH FILE NO DATE LISTED STATE HERITAGE PLACE ADDRESS LOCAL COUNCIL AREA 10321 8/11/1984 Goodlife Health Club (former Bank of Adelaide Head Office) 81 King William Street, ADELAIDE Adelaide 10411 11/12/1997 Shops (former Balfour's Shop and Cafe) 74 Rundle Mall, ADELAIDE Adelaide 10479 8/11/1984 Divett Mews (former Goode, Durrant & Co. Stables) Divett Place, ADELAIDE Adelaide 10480 8/11/1984 Cathedral Hotel Kermode Street, NORTH ADELAIDE Adelaide 10629 5/04/1984 Dwelling ('Admaston', originally 'Strelda') 219 Stanley Street, NORTH ADELAIDE Adelaide 1‐Mar Finniss Street and MacKinnon 10634 5/04/1984 Shop & Dwellings Parade, NORTH ADELAIDE Adelaide 10642 23/09/1982 Museum of Economic Botany, Adelaide Botanic Garden Park Lands, ADELAIDE Adelaide 10643 23/09/1982 Barr Smith Library (original building only), The University of Adelaide North Terrace, ADELAIDE Adelaide 10654 6/05/1982 Old Methodist Meeting Hall 25 Pirie Street, ADELAIDE Adelaide Pennington Terrace, NORTH 10756 24/07/1980 Walkley Cottage (originally Henry Watson's House), St Mark's College [modified 'Manning' House] ADELAIDE Adelaide 10760 26/11/1981 House ‐ 'Dimora', front fence and gates and southern boundary wall 120 East Terrace, ADELAIDE Adelaide 10761 28/05/1981 Former Centre for Performing Arts (former Teachers Training School), including Northern and Western Boundary Walls Grote Street, ADELAIDE Adelaide 10762 24/07/1980 Adelaide Remand -

Bird Report, 1982-1999 Graham Carpenter, Andrew Black
NOVEMBER 2003 93 BIRD REPORT, 1982-1999 GRAHAM CARPENTER, ANDREW BLACK, DAVID HARPER and PHILIPPAHORTON INTRODUCTION added, particularly details of specimens donated to and held by the South Australian Museum. For the nineteen years from 1963 to 1981, · Further details of these specimens are available periodic Bird Reports were collated and published from the Museum. in theSouth Australian Ornithologist(Glover et Priority for inclusion goes to reliable and al. 1964; Glover 1965-1975;Cox 1976a; N. Reid verifiable reports of birds rarely recorded for the 1976; J. Reid 1980; Bransbury 1984; note that state or region, namely those of birds recorded references for this section of the report appear on near or beyond their previously recognised range pp. 96-98). With increasing observations it be limits, unusual numbers and unusual seasonal came more difficult to do justice to all records occurrences, and breeding records. Note also that submitted to the South Australian Ornithological additional details, such as ecological data and Association. John Bransbury (1984) undertook field notes, may be available from the quarterly the demanding task to cover the five years 1977- SAOA Newsletters that are referred to by number 1981, a particularly active period when many of edition, or from the author of the record as SAOA members were engaged in compiling indicated by surnameand initial. records for the first Australian Bird Atlas The SAOA Newsletter Bird Notes and Bird (Blakers, Davies and Reilly 1984). Records for the period were collated and vetted The Bird Reports provided readers with a by Brian Glover until March 1984, Graham summary of interesting records for the year, thus Carpenter to March 1995 and David Harper to encouraging further records to confirm, extend or March 1999(SAOA 1982-1994 and 1994-1999).