Spice Models for Vacuum Tubes Using the Utracer
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

ECE 340 Lecture 22 : Space Charge at a Junction
ECE 340 Lecture 22 : Space Charge at a Junction Class Outline: •Space Charge Region Things you should know when you leave… Key Questions • What is the space charge region? • What are the important quantities? • How are the important quantities related to one another? • How would bias change my analysis? M.J. Gilbert ECE 340 – Lecture 22 10/12/11 Space Charge Region To gain a qualitative understanding of the solution for the electrostatic variables we need Poisson’s equation: Most times a simple closed form solution will not be possible, so we need an approximation from which we can derive other relations. Consider the following… Doping profile is known •To obtain the electric field and potential we need to integrate. •However, we don’t know the electron and hole concentrations as a function of x. •Electron and hole concentrations are a function of the potential which we do not know until we solve Poisson’s equation. Use the depletion approximation… M.J. Gilbert ECE 340 – Lecture 22 10/12/11 Space Charge Region What does the depletion approximation tell us… 1. The carrier concentrations are assumed to be negligible compared to the net doping concentrations in the junction region. 2. The charge density outside the depletion region is taken to be identically zero. Poisson equation becomes… Must xp = xn? M.J. Gilbert ECE 340 – Lecture 22 10/12/11 Space Charge Region We are already well aware of the formation of the space charge region… The space charge region is characterized by: Na < Nd •Electrons and holes moving across the junction. -

Varian Mw 3 % H
ORNL/Sub-75/49438/2 BP n ^TfFl varian mw 3 % h NOTICE PORTIONS OF TV'!? HFTL0'' SHE M.I.HGIB'.E. IF lT~~rvnrT;irri*"rr?.--p. tf.3 iwaito'jia 1 co1;;/ -o psrrnii the broadest possible avail- ability. FINAL REPORT MILLIMETER WAVE STUDY PROGRAM u by H.R. JORY, E.L. LIEN and R.S. SYMONS ft, 0 {I Order No. Y-12 11Y-49438V j November 1975 report prepared by Varian Associates Palo Alto Microwave Tube Division 611 Hansen Way o Palo Alto, California 94303 under subcontract number 11Y-49438V ; for ' ' r>4 OAK RIDGE NATIONAL LABORATORY * ° Oak Ridge, Tennessee 37830 operated by UNION CARBIDE CORPORATION for the nrsTKIUUTiON 01? 'ijl;.;?!---''--^-'.^-^''' UNLLMIT DEPARTMENTS ENERGY FINAL REPORT MILLIMETER WAVE STUDY PROGRAM by H. R. Jory, E. L Lien and R, S. Symons - NOTICE- Urn report Mas piepated as an account, of worl; sponsored by die Untied Stales Government. Neither Die United State* not the United States Pepastment of l.nergy, tiar any of1 their employees, nnr any of then contractors. subcontractor or their employees, makes any warranty, express or implied, or assumes any legal liability oi responsibility for tlie accuracy, completeness of usefulness of any information, apparatus, product or process disclovd. or represents that its use would not mUmfe pnvately owned npjits. Order No, Y-12UY-49438V November 1975 « 0 " report prepared by Varian Associates Palo Alto Microwave Tube Division 611 Hansen Way Palo Alto, California 94303 K< under subcontract number 11Y-49438V for OAK RIDGE NATIONAL LABORATORY Oak.RitJge-J'ennessee 37830 c.-..operatedjby U N 10N CARBiDE^G0RP0RATI0N, o <J>c l . -

RESEARCH for DEVELOPMENT of THIN-FILM SPACE-CHARGE-LIMITED TRIODE DEVICES (U) by Kenneth G. Aubuchon, Peter Knoll and Rainer
RESEARCH FOR DEVELOPMENT OF THIN-FILM SPACE-CHARGE-LIMITED TRIODE DEVICES (U) BY Kenneth G. Aubuchon, Peter Knoll and Rainer Zuleeg May 1967 Distribution of this report is provided in the interest of information exchange and should not be construed as endorse- ment by NASA of the material presented. Responsibility for the contents resides in the organization that prepared it. Prepared under Contract No. NAS 12-144 by: Hughes Aircraft Company Applied Solid State Research Department Newport Beach, California Electronics Research Center National Aeronautics & Space Administration RESEARCH FOR DEVELOPMENT OF THIN-FILM SPACE-CHARGE-LIMITED TRIODE DEVICES (U) BY Kenneth G. Aubuchon, Peter Knoll and Rainer Zuleeg May 1967 Prepared under Contract No. NAS 12-144 by: Hughes Air craft Company Applied Solid State Research Department Newport Beach, California for Electronics Research Center National Aeronautics & Space Administration TABLE OF CONTENTS SECTION TITLE PAGE NO: ABSTRACT ii FORE WORD iii LIST OF ILLUSTRATIONS iv I MATERIAL PREPARATION AND ANALYSIS 1 A. Introduction 1 B. Literature Survey 1 C. Experimental 3 D. Results 6 E. Discussion 13 I1 DEVICE THEORY 18 I11 DEVICE DESIGN AND FABRICATION 20 A. Mask Design 20 B. Silicon Processing 24 C. Discussion of Processing Problems 25 D. Summary of Lots Fabricated 27 E. Discussion of Yield 29 IV DEVICE EVALUATION 32 A. Correlation Between Theory and Experiment 32 B. High Frequency Performance 42 C. Modes of Operation 49 D. High Temperature Stability 54 E. Radiation Effects 54 F. Noise 62 V CONCLUSION 64 LIST OF REFERENCES 66 ABSTRACT Silicon-on- sapphire space - charge-limited triodes were de signed and fabricated. -
Grid Pentode
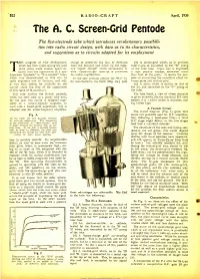
512 RADIO -CRAFT April, 1930 The A. C. Screen -Grid Pentode The five- electrode tube which introduces revolutionary possibili- ties into radio circuit design, with data as to its characteristics, and suggestions as to circuits adapted for its employment THE progress of tube development, charge to accelerate the flow of electrons (5) A screen -grid which, as in previous which has been rapid during the past from the filament and break up the nega- tuhe types, is connected to the "G" prong three years, made another spurt re- tive "space charge" which surrounded it. of the tube base. Upon this is impressed cently with the appearance of a new This "space- charge" hook -up is preferred a high positive voltage, somewhat lower American "pentode," or "five -element" tube; for audio amplification. than that of the plate. It serves the pur- which was demonstrated in this city to In the new pentode (styled the "P-1" by pose of eliminating the capacitive effect be- radio engineers late in January, and will, its manufacturer, the CeCo Mfg. Co.) both tween plate and control -grid. it was then stated, be available on the (6) A plate, which is similar to that of market alwut the time of the appearance the '24, and connected to the "P" prong of of this issue of RADIO-CRAFT. the tube. This tube (unlike the British pentode, The tube itself, a view of whose elements which has been used as a power tube only, is given herewith, fits the standard UY tube for the past two years) is designed espe- socket; it is 1 13/16 inches in diameter, and cially as a radio- frequency amplifier, to 51/4 inches high. -

Frequency Characteristics of the Electron-Tube Oscillation Generator
FREQUENCY CHARACTERISTICS OF THE ELECTRON—TUBE OSCILLATION GENERATOR BY RAY STUART QUICK B. S. University of California, 1916 THESIS Submitted in Partial Fulfillment of the Requirements for the Degree of MASTER OF SCIENCE IN ELECTRICAL ENGINEERING IN THE GRADUATE SCHOOL OF THE! UNIVERSITY OF ILLINOIS 1919 UNIVERSITY OF ILLINOIS THE GRADUATE SCHOOL I HEREBY RECOMMEND THAT THE THESIS PREPARED UNDER MY SUPERVISION BY Hay Stuart 4uick ENTITLED Jgraqstaney Character i st.i cs of the Electron-Tube Oscillation Generator BE ACCEPTED AS FULFILLING THIS PART OF THE REQUIREMENTS FOR THE DEGREE OF Master of Snionoe in Eleotri nol Engin eering . \Mm Head of Department Recommendation concurred in :! Committee on Final Examination* *Required for doctor's degree but not for master's 1 CONTENTS I INTRODUCTION Page 1. Scope of work 2 2. Historical review. 2 II THEORETICAL DISCUSSION OP PROBLEM 1. General principles of operation. 4 2. Circuits used. 6 3. Work of previous investigators. 6 4. Mathematical solution of circuits. 8 III APPARATUS AND METHODS 1. Electron- tubes used. 13 2. Circuit properties. 13 3. Frenuency determinations. 13 IV DATA AND EXPERIMENTAL RESULTS 1. Observed conditions necessary for constant eurrent and for oscillating eurrent. 36 2. Oscillograms. 36 3. Experimental results. 37 V CONCLUSIONS 1. Comparison of experimental ^nd theoretical results. 45 2. Suggestions as to future work 45 VI BIBLIOGRAPHY 47 2 I INTRODUCTIOU 1. Scope of Work. The development of the electron- tube ( also called three-electrode vacuum tube, vacuum- tube, thermionic amplifier, audion, etc. ) has brought to light many new and interest- ing problems. In using the tube as a source of continuous oscilla- tions it is desirable to be able to predetermine the frequency, wave-form and amplitude characteristics. -

Limits for Thermionic Emission from Leading Edges of Hypersonic Vehicles
10.2514/6.2016-0507 AIAA SciTech Forum 4-8 January 2016, San Diego, California, USA 54th AIAA Aerospace Sciences Meeting Limits for Thermionic Emission from Leading Edges of Hypersonic Vehicles Kyle M. Hanquist∗ and Iain D. Boydy Department of Aerospace Engineering, University of Michigan, Ann Arbor, MI Abstract Simulations of electron transpiration cooling (ETC) on the leading edge of a hypersonic vehicle using computational fluid dynamics (CFD) are presented. The thermionic emission boundary condition and electric field model including forced diffusion are discussed. Different analytical models are used to describe the plasma sheath physics in order to avoid resolving the sheath in the computational domain. The first analytical model does not account for emission in the sheath model, so the emission is only limited by the surface temperature. The second approach models the emissive surface as electronically floated, which greatly limits the emission. The last analytical approach biases the emissive surface, which makes it possible to overcome space-charge limits. Each approach is compared and a parametric study is performed to understand the effects that the material work function, freestream velocity, and leading edge geometry has on the ETC effect. The numerical results reveal that modeling the sheath as a floated surface results in the emission, and thus ETC benefits, being greatly limited. However, if the surface is negatively biased, the results show that the emission can overcome space-charge limits and achieve the ideal ETC benefits predicted by temperature limited emission. The study also shows that, along with negatively biasing the surface, emission is enhanced by increasing the number of electrons in the external flowfield by increasing the freestream velocity. -

Unusual Tubes
Unusual Tubes Tom Duncan, KG4CUY March 8, 2019 Tubes On Hand GAS-FILLED HIGH-VACUUM • Neon Lamp (NE-51) • Photomultiplier • Cold-cathode Voltage (931A) Regulator (0B2) • Magic Eye (1629) • Hot-cathode Thyratron • Low-voltage (12DY8) (884) • Space Charge (12K5) 2 Timeline of Related Events 1876, 1902 William Crookes Cathode Rays, Glow Discharge 1887 [1921] Hertz, Einstein Photoelectric Effect 1897 [1906] J. J. Thomson Electron identified 1920 Daniel Moore (GE) Voltage Regulator 1923 Joseph Slepian Secondary Emission (Westinghouse) 1928 Albert Hull, Irving Thyratron Langmuir (GE) [1928] Owen Richardson Thermionic Emission 1936 Vladimir Zworykin Photomultiplier (RCA) 1937 Allen DuMont Magic Eye 3 Neon Bulbs • Based on glow-discharge (coronal discharge) effect noticed by William Crookes around 1902. • Exhibit a negative incremental resistance over part of the operating range. • Light-sensitive: photo-ionization causes the ionization voltage to decrease with illumination (not generally a desirable characteristic). • Used as indicators , voltage regulators, relaxation oscillators , and the larger ones for illumination . 4 Neon Lamp/VR Tube Curves 80 Normal Abnormal Glow Glow 70 60 Townsend Discharge 50 Negative Resistance 40 Region 30 Volts across Device across Volts 20 10 Conduction Destroys Lamp Destroys Arc Conduction Arc Chart details (coronal) Glow depend on -5 element 10 -20 10 -15 10 -10 10 1 geometry and Current through Device (A) gas mixture. 5 Cold-Cathode Voltage Regulator Tubes • Very similar to neon bulbs: attention paid to increasing current-carrying capability and ensuring a constant forward voltage. • Gas sometimes includes radio-isotopes to reduce sensitivity to photo-ionization. • Developed at General Electric Research Labs by Daniel Moore around 1920. -

The Low Voltage Auto Boat Marine Radio Space-Charge Forgotten Vacuum Tube Set
The Low Voltage Auto Boat Marine Radio Space-Charge Forgotten Vacuum Tube Set OddMix TECHNOLOGY NOTES | Home | Arts | Books | Computers | Electronics | Free | Philately | OddMix Magazin | Specials | Technology | The Low Voltage Auto Boat Marine Radio Space-Charge Forgotten Vacuum Tube Set OddMix.com - Technical Note - TN090323 - by Karl Nagy As a solution to the tube type auto radio's persistent vibrator replacement and high voltage generation problems, leading tube manufacturers at the time - most notably RCA, Sylvania and others - developed vacuum tubes that could work off the 12V of an automobile battery without the need of any higher voltages. Around the end of the vacuum-tube era a set of about thirty tubes were designed and made available especially for low - 12 to 16V - B+ anode voltage use for the auto, boat and other vehicular radio designers. Figure 1. 12DZ6 Low Voltage These forgotten, but most useful are the; 12AD6, 12AE6, 12AE6A, Space Charge Tube 12AE7, 12AF6, 12AJ6, 12AL8, 12BL6, 12CN5, 12CX6, 12DE8, 12DK7, 12DL8, 12DS7, 12DS7A, 12DU7, 12DZ6, 12EA6, 12EC8, 12EG6, 12EK6, 12EL6, 12EM6, 12F8, 12FK6, 12FM6, 12FR8, 12FX8, 12FX8A, 12GA6, 12J8, 12K5, 12U7. Three of these tubes have an improved "A" version, but they are counted as a single type in the total count. The tubes in the above series are all rely on an old "forgotten" technology, the space-charge grid that was invented by Schottky around 1919. The space charge grid is an extra grid that is placed below the usual first or control grid. As the space charge grid is always connected to a positive voltage, usually to the anode potential, and since it is the closest to the tube's emitter, it greatly accelerates electron flow that translates to useable, higher anode current. -

Space-Charge-Limited Currents in Silicon Using Gold Contacts
AN ABSTRACT OF THE THESIS OF Alan Winthrop Ede for the Ph.D. in Electrical and Electronics Engineering presented on August 9, 1968. Title: Space -Charge -Limited Currents in Silicon Using Gold Contacts Redacted for privacy Abstract approved: James C. Looney - 1 Major professor The theoretical characteristics of space- charge- of limited currents in solids are reviewed, and a survey suitable dielectric materials and experimental space - charge- limited devices is presented. The properties of the gold -silicon contact as used in- in space- charge -limited devices were experimentally vestigated. It was found that the observed characteris- dif- tics could be explained on the basis that the gold fuses far enough into the silicon under fabrication reduces temperatures to set up a region of traps, which tc a very the space -charge- limited component of current low value. -limited An attempt to fabricate planar space- charge as the triodes using silicon as the dielectric and gold source and drain contacts was unsuccessful. Space- Charge- Limited Currents in Silicon Using Gold Contacts by Alan Winthrop Ede A THESIS submitted to Oregon State University in partial fulfillment of the requirements for the degree of Doctor of Philosophy June 1969 APPROVED: Redacted for privacy Associate Professor of Electrical and Electronics Engineering in charge of major Redacted for privacy and Eiead of Departmént tof Electrical Electronics V Engineering Redacted for privacy Dean of Graduate School Date thesis is presented August 9, 1968 Typed by Erma McClanathan ACKNOWLEDGMENT It is a pleasure for the author to express his gratitude to the many people whose assistance and advice were invaluable in this investigation. -

Space Charge Compensation and Electron Cloud Effects in Modern
Dottorato di Ricerca in Fisica degli Acceleratori Ciclo XXVIII Space Charge Compensation and Electron Cloud Effects in Modern High Intensity Proton Accelerators Thesis advisor Candidate Prof. Luigi Palumbo Roberto Salemme Supervisors Dr. Dirk Vandeplassche (SCK•CEN) Dr. Vincent Baglin (CERN) October 2016 Copyright ©2016 Roberto Salemme All rights reserved Preface The present work deals with two of the numerous challenges of modern and future particle accel- erators targeting high intensity proton beams: the beam dynamics of low energy intense beams in linear accelerators, which is influenced by space charge, and the beam induced multipacting causing the so called electron cloud in high energy circular accelerators. These themes have been the subject of my privileged involvement with two projects at the forefront of accelerator science and technology in the years 2013-2016. Space charge and its compensation was at the basis of the design of the Low Energy front-end of the Multi-purpose hYbrid Research Reactor for High-tech Applications (MYRRHA) accelerator project, which I joined in the period 2013-2014 in quality of Accelerator System Engineer at the Studiecentrum voor Kernenergie - Centre d'Etude´ de l'´energie Nuclaire (SCK•CEN), based in Mol and Louvain-la-Neuve, Belgium. The study of electron cloud effects and their mitigation comes from the involvement (since 2014) in the High Luminosity upgrade project of the Large Hadron Collider (LHC), in quality of Research Fellow of the Euro- pean Organization for Nuclear Research (CERN) and in charge of the COLD bore EXperiment (COLDEX), in Meyrin, Switzerland. The realization of this work is essentially based in the trust, encouragement and support of the people surrounding the professional and personal course of my doctoral undertaking, which was equally important, if not superior, to my dedication. -

Space Charge Limited Electron Emission from a Cu Surface Under Ultrashort Pulsed Laser Irradiation ͒ W
APPLIED PHYSICS LETTERS 96, 051121 ͑2010͒ Space charge limited electron emission from a Cu surface under ultrashort pulsed laser irradiation ͒ W. Wendelen,a D. Autrique, and A. Bogaerts Department of Chemistry, University of Antwerp, Universiteitsplein 1, 2610 Wilrijk, Belgium ͑Received 9 September 2009; accepted 15 December 2009; published online 5 February 2010͒ In this theoretical study, the electron emission from a copper surface under ultrashort pulsed laser irradiation is investigated using a one-dimensional particle in cell model. Thermionic emission as well as multiphoton photoelectron emission were taken into account. The emitted electrons create a negative space charge above the target; consequently the generated electric field reduces the electron emission by several orders of magnitude. The simulations indicate that the space charge effect should be considered when investigating electron emission related phenomena in materials under ultrashort pulsed laser irradiation of metals. © 2010 American Institute of Physics. ͓doi:10.1063/1.3292581͔ The recent development of femtosecond laser systems account in theoretical studies concerning electron emission resulted in a range of applications in different fields.1–4 In related phenomena in metals. spite of numerous efforts, the fundamental mechanisms of In the present letter, the space charge effect on electron ultrashort laser ablation are still subject to discussion.5–9 It emission from a copper surface is studied by means of a 1D 17 has been demonstrated that electron emission can influence collisionless PIC method. The simulations were performed the processes occurring during ultrashort ablation.10–12 For for a Gaussian pulse of 100 fs full width at half maximum example, the concept of Coulomb explosion ͑CE͒ was sug- and a wavelength of 800 nm, with an absorbed fluence of gested as a possible material removal mechanism during the 450 J/m2. -

Modelling and Diagnostics of Low Pressure Plasma Discharges
Lehrstuhl fur¨ Technische Elektrophysik Modelling and Diagnostics of Low Pressure Plasma Discharges Peter Scheubert Vollstandiger¨ Abdruck der von der Fakultat¨ fur¨ Elektrotechnik und Informationstechnik der Technischen Universitat¨ Munchen¨ zur Erlangung des akademischen Grades eines Doktors-Ingenieur (Dr.-Ing.) genehmigten Dissertation. Vorsitzender: Univ.-Prof. Dr.-Ing. habil. A. W. Koch Prufer¨ der Dissertation: 1. Univ.-Prof. Dr. rer. nat. G. Wachutka 2. Univ.-Prof. Dr. rer. nat R. P. Brinkmann 3. Priv.-Doz. Dr.-Ing., Dr.-Ing. habil. P. Awakowicz Die Dissertation wurde am 17:10:2001 bei der Technischen Universitat¨ Munchen¨ eingereicht und durch die Fakultat¨ fur¨ Elektrotechnik und Informationstechnik am 26:02:2002 angenommen. to all carrots growing on this planet Contents Zusammenfassung 1 Summary 3 Acknowledgements 4 1 Introduction 6 1.1 Application of low pressure, low temperature plasmas . 6 1.2 Modelling of low pressure plasmas . 7 1.3 Diagnostics . 9 1.4 An introductory approach to plasma models . 11 1.4.1 A simple Monte Carlo model . 11 1.4.2 Results . 13 1.4.3 Discussion . 16 2 Theory 19 2.1 Hydrodynamic models . 19 2.1.1 The Boltzmann equation and its moments . 20 2.1.2 Conservation of mass . 22 2.1.3 Conservation of momentum . 23 2.1.4 Conservation of energy . 24 2.2 Application of hydrodynamic models for low pressure plasmas . 25 2.2.1 General properties of low pressure plasma . 26 2.2.2 Conservation of mass . 27 2.2.3 Conservation of momentum . 28 2.2.4 Conservation of energy . 31 2.3 Energy transfer to the plasma .