(I) Randomization Inference
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
Districts of Ethiopia
Region District or Woredas Zone Remarks Afar Region Argobba Special Woreda -- Independent district/woredas Afar Region Afambo Zone 1 (Awsi Rasu) Afar Region Asayita Zone 1 (Awsi Rasu) Afar Region Chifra Zone 1 (Awsi Rasu) Afar Region Dubti Zone 1 (Awsi Rasu) Afar Region Elidar Zone 1 (Awsi Rasu) Afar Region Kori Zone 1 (Awsi Rasu) Afar Region Mille Zone 1 (Awsi Rasu) Afar Region Abala Zone 2 (Kilbet Rasu) Afar Region Afdera Zone 2 (Kilbet Rasu) Afar Region Berhale Zone 2 (Kilbet Rasu) Afar Region Dallol Zone 2 (Kilbet Rasu) Afar Region Erebti Zone 2 (Kilbet Rasu) Afar Region Koneba Zone 2 (Kilbet Rasu) Afar Region Megale Zone 2 (Kilbet Rasu) Afar Region Amibara Zone 3 (Gabi Rasu) Afar Region Awash Fentale Zone 3 (Gabi Rasu) Afar Region Bure Mudaytu Zone 3 (Gabi Rasu) Afar Region Dulecha Zone 3 (Gabi Rasu) Afar Region Gewane Zone 3 (Gabi Rasu) Afar Region Aura Zone 4 (Fantena Rasu) Afar Region Ewa Zone 4 (Fantena Rasu) Afar Region Gulina Zone 4 (Fantena Rasu) Afar Region Teru Zone 4 (Fantena Rasu) Afar Region Yalo Zone 4 (Fantena Rasu) Afar Region Dalifage (formerly known as Artuma) Zone 5 (Hari Rasu) Afar Region Dewe Zone 5 (Hari Rasu) Afar Region Hadele Ele (formerly known as Fursi) Zone 5 (Hari Rasu) Afar Region Simurobi Gele'alo Zone 5 (Hari Rasu) Afar Region Telalak Zone 5 (Hari Rasu) Amhara Region Achefer -- Defunct district/woredas Amhara Region Angolalla Terana Asagirt -- Defunct district/woredas Amhara Region Artuma Fursina Jile -- Defunct district/woredas Amhara Region Banja -- Defunct district/woredas Amhara Region Belessa -- -

Estimation of Elemental Concentrations of Ethiopia Coffee Arabica on Different Coffee Bean Varieties (Subspecies) Using Energy Dispersive X-Ray Florescence
International Journal of Scientific & Engineering Research Volume 9, Issue 4, April-2018 149 ISSN 2229-5518 Estimation of elemental concentrations of Ethiopia Coffee Arabica on different coffee bean Varieties (Subspecies) Using Energy Dispersive X-ray Florescence H. Masresha Feleke1*, Srinivasulu A1, K. Surendra1, B. Aruna1, Jaganmoy Biswas2, M. Sudershan2, A. D. P. Rao1, P. V. Lakshmi Narayana1 1. Dept. of Nuclear Physics, Andhra University, Visakhapatnam -530003, INDIA. 2. UGC-DAE Consortium for Scientific Research, Trace element lab, Salt Lake, Kolkata 700 098, India Abstract: Using Energy Dispersive X-ray Florescence (EDXRF) Elemental analysis, Coffee cherry of Arabica subspecies produced in crop years of 2015/2016 in nine different parts of coffee growing Area in Ethiopa were analyzed and has been found four major elements P, K, Ca, S and eight minor elements Mn, Fe, Cu, Zn, Se, Sr, Rb, Br from Twenty coffee Arabica subspecies. The Samples were washed; dried; Grinding with mortar and finally pelletized. EDXRF analysis were carried the energies of the X-rays emitted by the sample are measured using a Si- semiconductor detector and are processed by a pulse height analyzer. Computer analysis of this data yields an energy spectrum which defines the elemental composition of the sample. The system detection calibration and accuracy check was performed through different countries reported values and analysis of NIST certified reference materials SRM 1515 (Apple leaves). Most of coffee beans sample were found to be a good agreements towards NIST standards and different countries reported values. Meanwhile discussed the elemental concentration and their biological effects on human physiology. Keywords: Coffee Cherry,IJSER Subspecies coffee, Elemental Concentration and EDXRF 1. -

Oromia Region Administrative Map(As of 27 March 2013)
ETHIOPIA: Oromia Region Administrative Map (as of 27 March 2013) Amhara Gundo Meskel ! Amuru Dera Kelo ! Agemsa BENISHANGUL ! Jangir Ibantu ! ! Filikilik Hidabu GUMUZ Kiremu ! ! Wara AMHARA Haro ! Obera Jarte Gosha Dire ! ! Abote ! Tsiyon Jars!o ! Ejere Limu Ayana ! Kiremu Alibo ! Jardega Hose Tulu Miki Haro ! ! Kokofe Ababo Mana Mendi ! Gebre ! Gida ! Guracha ! ! Degem AFAR ! Gelila SomHbo oro Abay ! ! Sibu Kiltu Kewo Kere ! Biriti Degem DIRE DAWA Ayana ! ! Fiche Benguwa Chomen Dobi Abuna Ali ! K! ara ! Kuyu Debre Tsige ! Toba Guduru Dedu ! Doro ! ! Achane G/Be!ret Minare Debre ! Mendida Shambu Daleti ! Libanos Weberi Abe Chulute! Jemo ! Abichuna Kombolcha West Limu Hor!o ! Meta Yaya Gota Dongoro Kombolcha Ginde Kachisi Lefo ! Muke Turi Melka Chinaksen ! Gne'a ! N!ejo Fincha!-a Kembolcha R!obi ! Adda Gulele Rafu Jarso ! ! ! Wuchale ! Nopa ! Beret Mekoda Muger ! ! Wellega Nejo ! Goro Kulubi ! ! Funyan Debeka Boji Shikute Berga Jida ! Kombolcha Kober Guto Guduru ! !Duber Water Kersa Haro Jarso ! ! Debra ! ! Bira Gudetu ! Bila Seyo Chobi Kembibit Gutu Che!lenko ! ! Welenkombi Gorfo ! ! Begi Jarso Dirmeji Gida Bila Jimma ! Ketket Mulo ! Kersa Maya Bila Gola ! ! ! Sheno ! Kobo Alem Kondole ! ! Bicho ! Deder Gursum Muklemi Hena Sibu ! Chancho Wenoda ! Mieso Doba Kurfa Maya Beg!i Deboko ! Rare Mida ! Goja Shino Inchini Sululta Aleltu Babile Jimma Mulo ! Meta Guliso Golo Sire Hunde! Deder Chele ! Tobi Lalo ! Mekenejo Bitile ! Kegn Aleltu ! Tulo ! Harawacha ! ! ! ! Rob G! obu Genete ! Ifata Jeldu Lafto Girawa ! Gawo Inango ! Sendafa Mieso Hirna -

Examining the Economic Impacts of Climate Change on Net Crop Income in the Ethiopian Nile Basin: a Ricardian Fixed Effect Approach
sustainability Article Examining the Economic Impacts of Climate Change on Net Crop Income in the Ethiopian Nile Basin: A Ricardian Fixed Effect Approach Melese Mulu Baylie 1,2 and Csaba Fogarassy 3,* 1 Department of Economics, Debre Tabor University, Debra Tabor 272, Ethiopia; [email protected] 2 Department of Rural Development Engineering, Hungarian University of Agriculture and Life Sciences (Former Szent Istvan University), 2100 Gödöll˝o,Hungary 3 Institute of Sustainable Development and Farming, Hungarian University of Agriculture and Life Sciences (Former Szent Istvan University), 2100 Gödöll˝o,Hungary * Correspondence: [email protected] Abstract: Climate change affects crop production by distorting the indestructible productive power of the land. The objective of this study is to examine the economic impacts of climate change on net crop income in Nile Basin Ethiopia using a Ricardian fixed effect approach employing the International Food Policy Research Institute (IFPRI) household survey data for Ethiopia in 2015 and 2016. The survey samples were obtained through a three-stage stratified sampling technique from the five regions (Amhara, Tigray, Benishangul Gumuz, Oromia, and Southern Nation Nationality and People (SNNP) along the Nile basin Ethiopia. There are only 12–14% female household heads while there are 80–86% male households in the regions under study. In the regions, more than half of (64%) the Citation: Baylie, M.M.; Fogarassy, C. household heads are illiterate and almost only one-tenth of them (12%) had received remittance from Examining the Economic Impacts of abroad from their relatives or children. Crop variety adoption rate is minimal, adopted by the 31% Climate Change on Net Crop Income of farmers. -
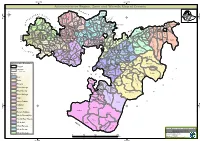
Administrative Region, Zone and Woreda Map of Oromia a M Tigray a Afar M H U Amhara a Uz N M
35°0'0"E 40°0'0"E Administrative Region, Zone and Woreda Map of Oromia A m Tigray A Afar m h u Amhara a uz N m Dera u N u u G " / m r B u l t Dire Dawa " r a e 0 g G n Hareri 0 ' r u u Addis Ababa ' n i H a 0 Gambela m s Somali 0 ° b a K Oromia Ü a I ° o A Hidabu 0 u Wara o r a n SNNPR 0 h a b s o a 1 u r Abote r z 1 d Jarte a Jarso a b s a b i m J i i L i b K Jardega e r L S u G i g n o G A a e m e r b r a u / K e t m uyu D b e n i u l u o Abay B M G i Ginde e a r n L e o e D l o Chomen e M K Beret a a Abe r s Chinaksen B H e t h Yaya Abichuna Gne'a r a c Nejo Dongoro t u Kombolcha a o Gulele R W Gudetu Kondole b Jimma Genete ru J u Adda a a Boji Dirmeji a d o Jida Goro Gutu i Jarso t Gu J o Kembibit b a g B d e Berga l Kersa Bila Seyo e i l t S d D e a i l u u r b Gursum G i e M Haro Maya B b u B o Boji Chekorsa a l d Lalo Asabi g Jimma Rare Mida M Aleltu a D G e e i o u e u Kurfa Chele t r i r Mieso m s Kegn r Gobu Seyo Ifata A f o F a S Ayira Guliso e Tulo b u S e G j a e i S n Gawo Kebe h i a r a Bako F o d G a l e i r y E l i Ambo i Chiro Zuria r Wayu e e e i l d Gaji Tibe d lm a a s Diga e Toke n Jimma Horo Zuria s e Dale Wabera n a w Tuka B Haru h e N Gimbichu t Kutaye e Yubdo W B Chwaka C a Goba Koricha a Leka a Gidami Boneya Boshe D M A Dale Sadi l Gemechis J I e Sayo Nole Dulecha lu k Nole Kaba i Tikur Alem o l D Lalo Kile Wama Hagalo o b r Yama Logi Welel Akaki a a a Enchini i Dawo ' b Meko n Gena e U Anchar a Midega Tola h a G Dabo a t t M Babile o Jimma Nunu c W e H l d m i K S i s a Kersana o f Hana Arjo D n Becho A o t -

The Impacts of Microcredit: Evidence from Ethiopia†
American Economic Journal: Applied Economics 2015, 7(1): 54–89 http://dx.doi.org/10.1257/app.20130475 The Impacts of Microcredit: Evidence from Ethiopia† By Alessandro Tarozzi, Jaikishan Desai, and Kristin Johnson* We use data from a randomized controlled trial conducted in 2003–2006 in rural Amhara and Oromiya Ethiopia to study the impacts of increasing access to microfinance( on a) number of socioeconomic outcomes, including income from agriculture, animal husbandry, nonfarm self-employment, labor supply, schooling and indicators of women’s empowerment. We document that despite sub- stantial increases in borrowing in areas assigned to treatment the null of no impact cannot be rejected for a large majority of outcomes. JEL G21, I20, J13, J16, O13, O16, O18 ( ) eginning in the 1970s, with the birth of the Grameen Bank in Bangladesh, Bmicrocredit has played a prominent role among development initiatives. Many proponents claim that microfinance has had enormously positive effects among borrowers. However, the rigorous evaluation of such claims of success has been complicated by the endogeneity of program placement and client selection, both common obstacles in program evaluations. Microfinance institutions MFIs typi- ( ) cally choose to locate in areas predicted to be profitable, and or where large impacts / are expected. In addition, individuals who seek out loans in areas served by MFIs and that are willing and able to form joint-liability borrowing groups a model often ( preferred by MFIs are likely different from others who do not along a number of ) observable and unobservable factors. Until recently, the results of most evaluations could not be interpreted as conclusively causal because of the lack of an appropriate control group see Brau and Woller 2004 and Armendáriz de Aghion and Morduch ( 2005 for comprehensive early surveys . -

OROMIA REGION - Regional 3W Map 07 December 2010
OROMIA REGION - Regional 3W Map 07 December 2010 CRS I SC-UK V Legend W Amhara S d S Farm Africa R S i E R C Benishangul R A V E CRS CARE MfM C GOAL C P n R W S o i I International Boundary SC-Denmark A , t Gumuz Afar C L c C P K Action Aid C A CARE Welthungerhilfe A CRS S U I M - I ! O C C IMC S S G S a CARE A WVE S Regional Boundary , SC-Denmark R R c m i SC-Denmark Dera C C a S r R f u u u c i C U E A Action Aid t r S m r n u f GOAL e R m R a r A m E IMC r i E C A b a I L L a R R Zonal Boundary K CARE ! f F o C Action Aid H s A a Hidabu Abote m r ! A A g a A r J x a a e A a C r Christian Aid C O d a C d r m O a r b O IMC Action Aid i W a M CA RE o J e I a G F G G G u e ! g L t n b r b e i a i i n i J o E S m u D a d Farm Africa Gerar Jarso R CARE Woreda Boundary E IMC u e p Kuyu E a ! Kiltu Kara m A i n ! o R ! S R C r ! a L Abay Chomen B Debre Libanos o ! Abuna G/Beret A M m M e A H e l o C en a m ks e ina r u Yaya Gulele Abichuna Gne'a C Ch Abe Dongoro ! a h s ! e i t c r a g f a u Nejo t IMC a ! r CRS No Data /No Intervention g E J ! W ! l a x Kombolcha o e R o ! d V e O b B i o ! ! s Guduru G J ib it Goro Gutu ! a r m b a Gudetu Kondole FHI Ke W a Mercy Corps b a s B u i ! r B Boji Dirmeji o t a Bila Seyo e i ! a r Jimma Genete l J d K L e g t s l Jeldu u E a ! d D ! u F Haro Maya e Guto Gida b M S u A m A o e B e M l R i d ! Boji Chekorsa Jimma Rare S ! D CARE GOAL CRS b a B b u A o Aleltu l e ! Kurfa Chele A g I O u f e e y G i u a S Mieso r Agriculture & Livestock i C r s t ! T a Mida KegnA a M Lalo Asabi im r K a ! ! G S Gobu -

Benishangul-Gumuz Region
Situation Analysis of Children and Women: Benishangul-Gumuz Region Situation Analysis of Children and Women: Benishangul-Gumuz Region ABSTRACT The Situation Analysis covers selected dimensions of child well-being in Benishangul-Gumuz Regional State. It builds on the national Situation Analysis of Children and Women in Ethiopia (2019) and on other existing research, with inputs from specialists in Government, UNICEF Ethiopia and other partners. It has an estimated population of approximately 1.1 million people, which constitutes 1.1% of the total Ethiopian population. The population is young: 13 per cent is under-five years of age and 44 per cent is under 18 years of age. Since 1999/00, Benishangul-Gumuz has experienced an impressive 28 percentage point decline in monetary poverty, but 27 per cent of the population are still poor; the second highest in the country after Tigray and higher than the national average of 24 per cent. SITUATION ANALYSIS OF CHILDREN AND WOMEN: BENISHANGUL-GUMUZ REGION 4 Food poverty continued a steep decline from 55 per cent in 1999/00 to 24 per cent in 2015/16; close to the national average of 25 per cent. In Benishangul-Gumuz, in 2014, only 1.1 per cent of rural households were in the PSNP compared to 11 per cent of households at the national level In 2011, the under-five mortality rate in Benishangul-Gumuz was the highest in Ethiopia (169 per 1,000 live births); this declined significantly, but is still very high: 96 deaths per 1,000 births, which is the second highest in the country after Afar. -

World Bank Document
Th e Fe d e r a l De mocr a tic R e p u b lic of E th iop ia Public Disclosure Authorized M i n i s t ry of A gri c u l t u re Public Disclosure Authorized E n vi ron me n t a l a n d S oc i a l M a n a ge me n t Fra me w ork ( E S M F) Ethiopia Resilient Landscapes and Livelihoods Project Additional Financing (P172462) Public Disclosure Authorized (Updated Final) December, 2019 Addis Ababa Public Disclosure Authorized Address:- Ministry of Agriculture: Sustainable Land Management Program (SLMP) P.O.Box 62347 Tel. +251-116-461300 Website: www.slmp.gov.et Addis Ababa, Ethiopia. This document is prepared by a team of consultants from the federal and regional program coordination units: Team members: Yebegaeshet Legesse (MSc.) Environmental Safeguard Specialist of National SLMP- Project Coordination Unit. Kewoldnesh Tsegaye (MSc.) Social Development (Social Safeguard and Gender) Specialist of National SLMP- Project Coordination Unit. Melaku Womber (MSc.) Environmental and Social Safeguard Specialist of Benishangul Gumuz region- Project Coordination Unit. Kiros G/Egziabher (MSc.) Environmental and Social Safeguard Specialist of Tigray region-Project Coordination Unit. Biel Dak (MSc.) Environmental and Social Safeguard Specialist of Gambella region- Project Coordination Unit. Ayana Yehuala (MSc.) Environmental and Social Safeguard Specialist of Amhara region- Project Coordination Unit. Alemayehu Solbamo (MSc.) Environmental and Social Safeguard Specialist of SNNPRS- Project Coordination Unit. ACKNOWLEDGEMENTS This document has reached its final version with a lot of efforts and contributions made from different partners. -

Annual Report
THE FEDERAL DEMOCRATIC REPUBLIC OF ETHIOPIA MINISTRY OF MINES AND ENERGY GEOLOGICAL SURVEY OF ETHIOPIA Annual Report 2000 Eth. C. July 2007 - June 2008 Cover Diagram Location of Hydrogeology, Engineering Geology and Geothermal project areas in 2000 Eth. C. Source: Hydrogeology, Engineering Geology and Geothermal Department, GSE. ii THE FEDERAL DEMOCRATIC REPUBLIC OF ETHIOPIA MINISTRY OF MINES GEOLOGICAL SURVEY OF ETHIOPIA Annual Report 2000 Eth. C. July 2007 - June 2008 Published by Technical Publication Team, Geoscience Information Center, GSE. iii Geological Survey of Ethiopia P. O. Box 2302, Addis Abeba, Ethiopia Tel: (251-1) 463325 Fax: (251-1) 463326, 712033 E-mail: [email protected] iv CONTENTS 1. Forward ........................................................................ viii 2. Introduction .................................................................................1 3. Regional Geology and Geochemistry ….................................... 2 4. Hydrogeology, Engineering Geology and Geothermal Exploration .........................................................…8 5. Economic Minerals Exploration and Evaluation .................................................................................. 17 6. Geophysical Activities ......................…………….....…............. 25 7. Drilling Work Performances...................................................... 33 8. Central Geological Laboratory Activities ................................... 36 9. Managing Geoscience Information ...........................................37 -

ETHIOPIA IDP Situation Report May 2019
ETHIOPIA IDP Situation Report May 2019 Highlights • Government return operations continue at full scale and sites are being dismantled. • Where security is assured and rehabilitation support provided, IDPs have opted to return to their areas of origin. IDPs who still feel insecure and have experienced trauma prefer to relocate elsewhere or integrate within the community. Management of IDP preferences differs in every IDP caseload. • There is minimal to no assistance in areas of return. Local authorities have requested international partner sup- port to address the gap. Meanwhile, public-private initiatives continue to fundraise for the rehabilitation of IDPs. • The living condition of the already vulnerable host communities has deteriorated having shared their limited resources with the IDPs for over a year. I. Displacement context Government IDP return operations have been implemented at full scale since early May 2019 following the 8 April 2019 announcement of the Federal Government’s Strategic Plan to Address Internal Displacement and a costed Re- covery/Rehabilitation Plan. By end May, most IDP sites/camps were dismantled, in particular in East/West Wollega and Gedeo/West Guji zones. Humanitarian partners have increased their engagement with Government at all levels aiming to improve the implementation of the Government return operation, in particular advocating for the returns to happen voluntarily, in safety, sustainably and with dignity. Overall, humanitarian needs remain high in both areas of displacement and of return. Most assistance in displace- ment areas is disrupted following the mass Government return operation and the dismantling of sites, while assis- tance in areas of return remain scant to non-existent, affecting the sustainability of the returns. -

31052019 West & East Wellega & Kemashi Assosa (BGR
ETHIOPIA East &West Wellega zone(Oromia Region)and Kamashi zone(BGR) IDP Returnees Snapshot As of 31 May 2019 Following the inter-communal conflict Awi that erupted in Kamashi zone (BGR) on West Gojam 26 September, 2018 there was massive displacement of people (majority being ± women and children) triggering protec- Metekel tion concerns. KEY FIGURES DISPLACEMENT Sherkole Kurmuk number of IDPs were living in collective 228,954 Sodal (36,320 HH) sites in East & West Wellega, 145, 685 IDPs were living in East Wellega and 83,269 IDPs 9,802 Homosha were living in West Wellega (Source: Menge DRMO) 14,473 Asosa Oda Bilidigilu 354 IDP Returnees Ibantu 26,710 Kiremu In East Wollega, 89,265 IDPs have returned to their place of origin Assosa in East Wellega zone along border areas of Oromia region. 26,985 Yaso 30,468 East Wellega Gida Ayana IDPs have returned to their place of origin in Yaso and Belo Jegan- 4,480 2,592 foy woredas of Kamashi Zone (BGR) from East Wellega Zone. Over- Bambasi Mendi Town Agalometi Haro Limu all,80% of the IDPs from East Wollega have returned to their place Mana Sibu of origin along the border of Oromia region and Kamashi zone Kiltu Kara 14,020 Limu (Oromia) Kemashi (BGR). 20% of the IDPs are living within the host community. Leta Sibu Nejo 12,744 5,986 In West Wollega, 50, 555 IDPs have returned to their place of origin 5,187 Maokomo Special West Wellega Nejo Town Kamashi in Oda Bildigilu Woreda of Assosa Zone and Sedal, Agelo Meti and 9,743 145,685 Indv.