DOCSLIB.ORG

Homological Algebra Notes Sean Sather-Wagstaff

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Homological Algebra Notes Sean Sather-Wagstaff Homological Algebra Notes Sean Sather-Wagstaff Department of Mathematics, 300 Minard Hall, North Dakota State University, Fargo, North Dakota 58105-5075, USA E-mail address: [email protected] URL: http://math.ndsu.nodak.edu/faculty/ssatherw/ September 8, 2009. Contents Introduction September 8, 2009 v Format of these notes vii Acknowledgements viii Notation and conventions viii Chapter I. Universal Constructions September 8, 2009 1 I.1. Finitely Generated Free Modules 1 I.2. Products of Modules 3 I.3. Coproducts of Modules 5 I.4. Localization 7 I.5. Hom: Functoriality and Localization 10 Chapter II. Tensor Products September 8, 2009 21 II.1. Existence and Uniqueness 21 II.2. Functoriality and Base-Change 25 II.3. Commutativity and Associativity 31 II.4. Right-Exactness 35 II.5. Hom-Tensor Adjointness 40 Chapter III. Injective, Projective, and Flat Modules September 8, 2009 43 III.1. Injective and Projective Modules 43 III.2. Flat Modules 51 III.3. Faithfully Flat Modules 58 III.4. Power Series Rings 60 III.5. Flat Ring Homomorphisms 65 III.6. Completions: A Survey 69 III.7. Completions: Some Details 69 Chapter IV. Homology, Resolutions, Ext and Tor September 8, 2009 71 IV.1. Chain Complexes and Homology 71 IV.2. Resolutions 76 IV.3. Ext-Modules 79 IV.4. Tor-Modules 84 IV.5. Epilogue 86 Chapter V. Depth September 8, 2009 89 V.1. Assumptions 89 V.2. Associated Primes and Supports of Modules 91 V.3. Prime Filtrations 96 V.4. Prime Avoidance and Nakayama's Lemma 100 V.5. Regular Sequences and Ext 105 iii iv CONTENTS V.6. Four Lemmas 112 Chapter VI. Chain Maps and Induced Maps on Ext and Tor September 8, 2009 115 VI.1. Chain Maps 115 VI.2. Isomorphisms for Ext and Tor 117 VI.3. Liftings of Resolutions 121 VI.4. Induced Chain Maps 125 VI.5. Ext-maps via projective resolutions 131 VI.6. Ext-maps via injective resolutions 135 VI.7. Tor-maps 137 Chapter VII. Ext, Tor, and Homological Dimensions September 8, 2009 143 VII.1. Assumptions 143 VII.2. Depth and Dimension 143 VII.3. Ext and Projective Dimension 146 VII.4. Tor and Projective Dimension 152 VII.5. Ext and Injective Dimension 154 VII.6. Tor and Flat Dimension 157 Chapter VIII. Long Exact Sequences September 8, 2009 161 VIII.1. General Long Exact Sequences 161 VIII.2. Long Exact Sequences in Ext and Tor 167 VIII.3. Horseshoe Lemmas 170 VIII.4. Mapping Cones 174 VIII.5. Ext, Tor, and Resolutions 179 VIII.6. Koszul Complexes 183 VIII.7. Epilogue: Tor and Torsion 192 Chapter IX. Depth and Homological Dimensions September 8, 2009 195 IX.1. Projective Dimension and Regular Sequences 195 IX.2. The Auslander-Buchsbaum Formula 197 IX.3. Depth and Flat Ring Homomorphisms 200 IX.4. Injective Dimension and Regular Sequences 205 Chapter X. Regular Local Rings September 8, 2009 207 X.1. Background from Dimension Theory 207 X.2. Definitions and Basic Properties 209 X.3. Theorems of Auslander, Buchsbaum and Serre 212 X.4. Regularity and Flat Local Homomorphisms 216 Index 221 Bibliography 225 Introduction September 8, 2009 An important question to ask (and re-ask) when one is learning a new subject is, \What does this subject do for me?" A complete answer to this question is usually hard to give, especially because the answer almost certainly depends on the interests of the person asking it. Here are a couple of motivating answers for the (commutative) algebraist who is thinking about learning some homological algebra. Let R be a commutative ring (with identity). Ext and Tor. Given an R-module N and an exact sequence of R-modules 0 ! M 0 ! M ! M 00 ! 0 (&) the operators HomR(−; −) and − ⊗R − give rise to three exact sequences 0 00 0 ! HomR(N; M ) ! HomR(N; M) ! HomR(N; M )(∗) 00 0 0 ! HomR(M ;N) ! HomR(M; N) ! HomR(M ;N)(y) 0 00 M ⊗R N ! M ⊗R N ! M ⊗R N ! 0: (#) One may be tempted to feel cheated by the loss of zeroes. When N is projective, we get to add \! 0" onto the first sequence, and we get to add \0 !" onto the last sequence. And when N is injective, we get to add \! 0" onto the second sequence. But why are the last maps in the first two sequences not surjective in general? And why is the first map in the last sequence not injective? The answers to these questions are given in terms of Ext and Tor. There are two sequences of operators n R fExtR(−; −) j n = 1; 2;:::g and fTorn (−; −) j n = 1; 2;:::g that satisfy the following properties. n (a) An R-moduleN is projective if and only if ExtR(N; −) = 0 for all n > 1. (b) Given an R-module N and an exact sequence of R-modules (&) there is a \long exact sequence" 0 00 0 ! HomR(N; M ) ! HomR(N; M) ! HomR(N; M ) 1 0 1 1 00 −! ExtR(N; M ) −! ExtR(N; M) −! ExtR(N; M ) !··· n 0 n n 00 · · · −! ExtR(N; M ) −! ExtR(N; M) −! ExtR(N; M ) !··· : n (c) An R-module N is injective if and only if ExtR(−;N) = 0 for all n > 1. v vi INTRODUCTION September 8, 2009 (d) Given an R-module N and an exact sequence of R-modules (&) there is a \long exact sequence" 00 0 0 ! HomR(M ;N) ! HomR(M; N) ! HomR(M ;N) 1 00 1 1 0 −! ExtR(M ;N) −! ExtR(M; N) −! ExtR(M ;N) !··· n 00 n n 0 · · · −! ExtR(M ;N) −! ExtR(M; N) −! ExtR(M ;N) !··· : R (e) An R-module N is flat if and only if Torn (−;N) = 0 for all n > 1. (f) Given an R-module N and an exact sequence of R-modules (&) there is a \long exact sequence" R 0 R R 00 ···! Torn (M ;N) ! Torn (M; N) ! Torn (M ;N) !··· R 0 R R 00 ···! Tor1 (M ;N) ! Tor1 (M; N) ! Tor1 (M ;N) 0 00 −−! M ⊗R N −−−! M ⊗R N −−−! M ⊗R N ! 0: The sequence in (b) shows exactly what is missing from (∗). Furthermore, when N is projective, item (a) explains exactly why we can add \! 0" onto the sequence (∗). Similar comments hold for the sequence (y); also for (#) once one knows that every projective R-module is flat. The constructions of Ext and Tor are homological in nature. So, the first answer to the question of what homological algebra gives you is: it shows you what has been missing and gives a full explanation for some special-case behaviors. Another thing homological algebra gives you is invariants for studying rings and modules. Consider the following example. How do you distinguish between the vector spaces R2 and R3? Answer: by looking at the dimensions. The first one has dimension 2 and the second one has dimension 3. Therfore, they are not isomorphic. In the study of modules over a commutative ring, even when there is a rea- sonable vector space dimension, it may not be enough to distinguish between non-isomorphic R-modules. Take for example the ring R[X; Y ] and the modules R[X; Y ]=(X; Y 2) and R[X; Y ]=(X2;Y ). Each has vector space dimension 2 (over R) but they are not isomorphic as R-modules. Homological algebra gives you new invariants (numbers, functors, categories, etc.) to attach to an R-module that give you the power to detect (sometimes) when two modules are non-isomorphic. Of course, in the last example, one doesn't need to work very hard to see why the modules are not isomorphic. But in other situations, these homological invariants can be extremely powerful tools for the study of rings and modules. And these tools are so useful that many of them have become indispensable, almost unavoidable, items for the ring theorists' toolbox. Regular sequences. Assume that R is noetherian and local with maximal ideal m. A sequence x1; : : : ; xn 2 m is R-regular if (1) the element x1 is a non-zero- divisor on R, and (2) for i = 1; : : : ; n − 1 the element xi+1 is a non-zero-divisor on the quotient R=(x1; : : : ; xi). The fact that R is noetherian implies that every R-regular sequence can be extended to a maximal one, that is, to one that cannot be further extended. It is not obvious, though, whether two maximal R-regular sequences have the same length. The fact that this works is a consequence of the following Ext-characterization: For each integer n > 1, the following conditions are equivalent: FORMAT OF THESE NOTES vii i (i) We have ExtR(R=m;M) = 0 for all i < n; (ii) Every R-regular sequence in m of length 6 n can be extended to an R-regular sequence in m of length n; and (iii) There exists an R-regular sequence of length n in m. The depth of a R is the length of a maximal R-regular sequence in m. It is the subject of Chapter V. This is a handy invariant for induction arguments because when x 2 m is an R-regular element, the rings R and R=xR are homologically very similar, but we have depth(R=xR) = depth(R) − 1. Hence, if one is proving a result by induction on depth(R), one can often apply the induction hypothesis to R=xR and then show that the desired conclusion for R=xR implies the desired conclusion for R.
Load more

Recommended publications
  • Homological Algebra
    Homological Algebra Donu Arapura April 1, 2020 Contents 1 Some module theory3 1.1 Modules................................3 1.6 Projective modules..........................5 1.12 Projective modules versus free modules..............7 1.15 Injective modules...........................8 1.21 Tensor products............................9 2 Homology 13 2.1 Simplicial complexes......................... 13 2.8 Complexes............................... 15 2.15 Homotopy............................... 18 2.23 Mapping cones............................ 19 3 Ext groups 21 3.1 Extensions............................... 21 3.11 Projective resolutions........................ 24 3.16 Higher Ext groups.......................... 26 3.22 Characterization of projectives and injectives........... 28 4 Cohomology of groups 32 4.1 Group cohomology.......................... 32 4.6 Bar resolution............................. 33 4.11 Low degree cohomology....................... 34 4.16 Applications to finite groups..................... 36 4.20 Topological interpretation...................... 38 5 Derived Functors and Tor 39 5.1 Abelian categories.......................... 39 5.13 Derived functors........................... 41 5.23 Tor functors.............................. 44 5.28 Homology of a group......................... 45 1 6 Further techniques 47 6.1 Double complexes........................... 47 6.7 Koszul complexes........................... 49 7 Applications to commutative algebra 52 7.1 Global dimensions.......................... 52 7.9 Global dimension of
    [Show full text]
  • Homological Algebra Over the Representation Green Functor
    Homological Algebra over the Representation Green Functor SPUR Final Paper, Summer 2012 Yajit Jain Mentor: John Ullman Project suggested by: Mark Behrens February 1, 2013 Abstract In this paper we compute Ext RpF; F q for modules over the representation Green functor R with F given to be the fixed point functor. These functors are Mackey functors, defined in terms of a specific group with coefficients in a commutative ring. Previous work by J. Ventura [1] computes these derived k functors for cyclic groups of order 2 with coefficients in F2. We give computations for general cyclic groups with coefficients in a general field of finite characteristic as well as the symmetric group on three elements with coefficients in F2. 1 1 Introduction Mackey functors are algebraic objects that arise in group representation theory and in equivariant stable homotopy theory, where they arise as stable homotopy groups of equivariant spectra. However, they can be given a purely algebraic definition (see [2]), and there are many interesting problems related to them. In this paper we compute derived functors Ext of the internal homomorphism functor defined on the category of modules over the representation Green functor R. These Mackey functors arise in Künneth spectral sequences for equivariant K-theory (see [1]). We begin by giving definitions of the Burnside category and of Mackey functors. These objects depend on a specific finite group G. It is possible to define a tensor product of Mackey functors, allowing us to identify ’rings’ in the category of Mackey functors, otherwise known as Green functors. We can then define modules over Green functors.
    [Show full text]
  • Homological Algebra in Characteristic One Arxiv:1703.02325V1
    Homological algebra in characteristic one Alain Connes, Caterina Consani∗ Abstract This article develops several main results for a general theory of homological algebra in categories such as the category of sheaves of idempotent modules over a topos. In the analogy with the development of homological algebra for abelian categories the present paper should be viewed as the analogue of the development of homological algebra for abelian groups. Our selected prototype, the category Bmod of modules over the Boolean semifield B := f0, 1g is the replacement for the category of abelian groups. We show that the semi-additive category Bmod fulfills analogues of the axioms AB1 and AB2 for abelian categories. By introducing a precise comonad on Bmod we obtain the conceptually related Kleisli and Eilenberg-Moore categories. The latter category Bmods is simply Bmod in the topos of sets endowed with an involution and as such it shares with Bmod most of its abstract categorical properties. The three main results of the paper are the following. First, when endowed with the natural ideal of null morphisms, the category Bmods is a semi-exact, homological category in the sense of M. Grandis. Second, there is a far reaching analogy between Bmods and the category of operators in Hilbert space, and in particular results relating null kernel and injectivity for morphisms. The third fundamental result is that, even for finite objects of Bmods the resulting homological algebra is non-trivial and gives rise to a computable Ext functor. We determine explicitly this functor in the case provided by the diagonal morphism of the Boolean semiring into its square.
    [Show full text]
  • Categorical-Algebraic Methods in Group Cohomology
    Categorical-algebraic methods in group cohomology Tim Van der Linden Fonds de la Recherche Scientifique–FNRS Université catholique de Louvain 20th of July 2017 | Vancouver | CT2017 § My concrete aim: to understand (co)homology of groups. § Several aspects: § general categorical versions of known results; § problems leading to further development of categorical algebra; § categorical methods leading to new results for groups. Today, I would like to § explain how the concept of a higher central extension unifies the interpretations of homology and cohomology; § give an overview of some categorical-algebraic methods used for this aim. This is joint work with many people, done over the last 15 years. Group cohomology via categorical algebra In my work I mainly develop and apply categorical algebra in its interactions with homology theory. § Several aspects: § general categorical versions of known results; § problems leading to further development of categorical algebra; § categorical methods leading to new results for groups. Today, I would like to § explain how the concept of a higher central extension unifies the interpretations of homology and cohomology; § give an overview of some categorical-algebraic methods used for this aim. This is joint work with many people, done over the last 15 years. Group cohomology via categorical algebra In my work I mainly develop and apply categorical algebra in its interactions with homology theory. § My concrete aim: to understand (co)homology of groups. Today, I would like to § explain how the concept of a higher central extension unifies the interpretations of homology and cohomology; § give an overview of some categorical-algebraic methods used for this aim. This is joint work with many people, done over the last 15 years.
    [Show full text]
  • An Introduction to Homological Algebra
    An Introduction to Homological Algebra Aaron Marcus September 21, 2007 1 Introduction While it began as a tool in algebraic topology, the last fifty years have seen homological algebra grow into an indispensable tool for algebraists, topologists, and geometers. 2 Preliminaries Before we can truly begin, we must first introduce some basic concepts. Throughout, R will denote a commutative ring (though very little actually depends on commutativity). For the sake of discussion, one may assume either that R is a field (in which case we will have chain complexes of vector spaces) or that R = Z (in which case we will have chain complexes of abelian groups). 2.1 Chain Complexes Definition 2.1. A chain complex is a collection of {Ci}i∈Z of R-modules and maps {di : Ci → Ci−1} i called differentials such that di−1 ◦ di = 0. Similarly, a cochain complex is a collection of {C }i∈Z of R-modules and maps {di : Ci → Ci+1} such that di+1 ◦ di = 0. di+1 di ... / Ci+1 / Ci / Ci−1 / ... Remark 2.2. The only difference between a chain complex and a cochain complex is whether the maps go up in degree (are of degree 1) or go down in degree (are of degree −1). Every chain complex is canonically i i a cochain complex by setting C = C−i and d = d−i. Remark 2.3. While we have assumed complexes to be infinite in both directions, if a complex begins or ends with an infinite number of zeros, we can suppress these zeros and discuss finite or bounded complexes.
    [Show full text]
  • A Primer on Homological Algebra
    A Primer on Homological Algebra Henry Y. Chan July 12, 2013 1 Modules For people who have taken the algebra sequence, you can pretty much skip the first section... Before telling you what a module is, you probably should know what a ring is... Definition 1.1. A ring is a set R with two operations + and ∗ and two identities 0 and 1 such that 1. (R; +; 0) is an abelian group. 2. (Associativity) (x ∗ y) ∗ z = x ∗ (y ∗ z), for all x; y; z 2 R. 3. (Multiplicative Identity) x ∗ 1 = 1 ∗ x = x, for all x 2 R. 4. (Left Distributivity) x ∗ (y + z) = x ∗ y + x ∗ z, for all x; y; z 2 R. 5. (Right Distributivity) (x + y) ∗ z = x ∗ z + y ∗ z, for all x; y; z 2 R. A ring is commutative if ∗ is commutative. Note that multiplicative inverses do not have to exist! Example 1.2. 1. Z; Q; R; C with the standard addition, the standard multiplication, 0, and 1. 2. Z=nZ with addition and multiplication modulo n, 0, and 1. 3. R [x], the set of all polynomials with coefficients in R, where R is a ring, with the standard polynomial addition and multiplication. 4. Mn×n, the set of all n-by-n matrices, with matrix addition and multiplication, 0n, and In. For convenience, from now on we only consider commutative rings. Definition 1.3. Assume (R; +R; ∗R; 0R; 1R) is a commutative ring. A R-module is an abelian group (M; +M ; 0M ) with an operation · : R × M ! M such that 1 1.
    [Show full text]
  • Lecture Notes on Homological Algebra Hamburg SS 2019
    Lecture notes on homological algebra Hamburg SS 2019 T. Dyckerhoff June 17, 2019 Contents 1 Chain complexes 1 2 Abelian categories 6 3 Derived functors 15 4 Application: Syzygy Theorem 33 5 Ext and extensions 35 6 Quiver representations 41 7 Group homology 45 8 The bar construction and group cohomology in low degrees 47 9 Periodicity in group homology 54 1 Chain complexes Let R be a ring. A chain complex (C•; d) of (left) R-modules consists of a family fCnjn 2 Zg of R-modules equipped with R-linear maps dn : Cn ! Cn−1 satisfying, for every n 2 Z, the condition dn ◦ dn+1 = 0. The maps fdng are called differentials and, for n 2 Z, the module Cn is called the module of n-chains. Remark 1.1. To keep the notation light we usually abbreviate C• = (C•; d) and simply write d for dn. Example 1.2 (Syzygies). Let R = C[x1; : : : ; xn] denote the polynomial ring with complex coefficients, and let M be a finitely generated R-module. (i) Suppose the set fa1; a2; : : : ; akg ⊂ M generates M as an R-module, then we obtain a sequence of R-linear maps ' k ker(') ,! R M (1.3) 1 k 1 where ' is defined by sending the basis element ei of R to ai. We set Syz (M) := ker(') and, for now, ignore the fact that this R-module may depend on the chosen generators of M. Following D. Hilbert, we call Syz1(M) the first syzygy module of M. In light of (1.3), every element of Syz1(M), also called syzygy, can be interpreted as a relation among the chosen generators of M as follows: every element 1 of r 2 Syz (M) can be expressed as an R-linear combination λ1e1 +λ2e2 +···+λkek of the basis elements of Rk.
    [Show full text]
  • Lectures on Homological Algebra
    Lectures on Homological Algebra Weizhe Zheng Morningside Center of Mathematics Academy of Mathematics and Systems Science, Chinese Academy of Sciences Beijing 100190, China University of the Chinese Academy of Sciences, Beijing 100049, China Email: [email protected] Contents 1 Categories and functors 1 1.1 Categories . 1 1.2 Functors . 3 1.3 Universal constructions . 7 1.4 Adjunction . 11 1.5 Additive categories . 16 1.6 Abelian categories . 21 1.7 Projective and injective objects . 30 1.8 Projective and injective modules . 32 2 Derived categories and derived functors 41 2.1 Complexes . 41 2.2 Homotopy category, triangulated categories . 47 2.3 Localization of categories . 56 2.4 Derived categories . 61 2.5 Extensions . 70 2.6 Derived functors . 78 2.7 Double complexes, derived Hom ..................... 83 2.8 Flat modules, derived tensor product . 88 2.9 Homology and cohomology of groups . 98 2.10 Spectral objects and spectral sequences . 101 Summary of properties of rings and modules 105 iii iv CONTENTS Chapter 1 Categories and functors Very rough historical sketch Homological algebra studies derived functors between • categories of modules (since the 1940s, culminating in the 1956 book by Cartan and Eilenberg [CE]); • abelian categories (Grothendieck’s 1957 T¯ohokuarticle [G]); and • derived categories (Verdier’s 1963 notes [V1] and 1967 thesis of doctorat d’État [V2] following ideas of Grothendieck). 1.1 Categories Definition 1.1.1. A category C consists of a set of objects Ob(C), a set of morphisms Hom(X, Y ) for every pair of objects (X, Y ) of C, and a composition law, namely a map Hom(X, Y ) × Hom(Y, Z) → Hom(X, Z), denoted by (f, g) 7→ gf (or g ◦ f), for every triple of objects (X, Y, Z) of C.
    [Show full text]
  • Homological Algebra in Abelian Categories
    Homological Algebra in Abelian Categories Rylee Lyman March 3, 2019 1 Preliminaries Recall that a category is a collection of objects with arrows between them. We use the word \collection" advisedly, making no claim that we are dealing with sets. We require each object A to have an associated arrow A 1A A called the identity. We also require composition of arrows to be defined whenever it makes sense, and we require this composition to be associative. Furthermore, given f : A ! B, f1A = f = 1Bf We follow the treatment in [Mac71] to which the curious reader is referred. In category theory, a dual statement is one in which all the arrows have been reversed. For example, an arrow m is monic if it is \right-cancellative," i.e. mf = mg =) f = g The dual notion is an epi. An isomorphism is an arrow that has a two-sided inverse. Exercise 1. Isomorphisms are both monic and epi The converse does not always hold. A standard example is the inclusion Z ! Q in the category of rings. An object z is initial if, given another object t, there is a unique arrow z A: Dually, an object is terminal if there is a unique arrow to the object from any given object. A zero object is one that is both initial and terminal. Exercise 2. If z and w are both initial, terminal, or zero objects, there exists a unique isomorphism z ! w. We will denote our zero objects as 0, as well as any arrow that factors through the zero object.
    [Show full text]
  • Homotopical and Homological Algebra
    HOMOTOPICAL AND HOMOLOGICAL ALGEBRA PATRICK K. MCFADDIN Contents 1. Introduction 1 2. Homotopical Algebra 2 2.1. Model Categories 2 2.2. The Homotopy Category 3 2.3. (Co)Fibrant Replacement 4 3. Homological Algebra 5 3.1. Derived Categories 5 3.2. Derived Functors 5 4. Duality in Category O 6 4.1. Duality in O 7 References 8 1. Introduction In the algebraic setting, one main method used in analyzing a given object is to in- vestigate maps into and out of it. For example, the study of abelian categories consists of considering functors from a given abelian category into a well-behaved category such as Ab, the category of abelian groups and group homomorphisms. In this context, one property we can investigate is the exactness of such a functor. One example of an abelian category is the category of modules over a ring Λ, denoted Mod(Λ). In fact, this is really the only example (see the Freyd-Mitchell Theorem or Mitchell's Embedding Theorem). In studying these categories, homological methods can be used to determine how far certain functors are from being exact. The objects which measure this non-exactness are called derived functors. Unfortunately, these categories can be much too large to be the subject of a fruitful study (and may cause set-theoretic difficulties), so often our analysis must be reduced to the study of a more easily understood subcategory which still captures enough information to be useful. For example, in the algebraic K-theory of rings, to analyze a ring Λ, one restricts themselves to the study of finitely generated projective modules over Λ.
    [Show full text]
  • Homological Algebra
    Homological Algebra Andrew Kobin Fall 2014 / Spring 2017 Contents Contents Contents 0 Introduction 1 1 Preliminaries 4 1.1 Categories and Functors . .4 1.2 Exactness of Sequences and Functors . 10 1.3 Tensor Products . 17 2 Special Modules 24 2.1 Projective Modules . 24 2.2 Modules Over Noetherian Rings . 28 2.3 Injective Modules . 31 2.4 Flat Modules . 38 3 Categorical Constructions 47 3.1 Products and Coproducts . 47 3.2 Limits and Colimits . 49 3.3 Abelian Categories . 54 3.4 Projective and Injective Resolutions . 56 4 Homology 60 4.1 Chain Complexes and Homology . 60 4.2 Derived Functors . 65 4.3 Derived Categories . 70 4.4 Tor and Ext . 79 4.5 Universal Coefficient Theorems . 90 5 Ring Homology 93 5.1 Dimensions of Rings . 93 5.2 Hilbert's Syzygy Theorem . 97 5.3 Regular Local Rings . 101 5.4 Differential Graded Algebras . 103 6 Spectral Sequences 110 6.1 Bicomplexes and Exact Couples . 110 6.2 Spectral Sequences . 113 6.3 Applications of Spectral Sequences . 119 7 Group Cohomology 128 7.1 G-Modules . 128 7.2 Cohomology of Groups . 130 7.3 Some Results for the First Group Cohomology . 133 7.4 Group Extensions . 136 7.5 Central Simple Algebras . 139 7.6 Classifying Space . 142 i Contents Contents 8 Sheaf Theory 144 8.1 Sheaves and Sections . 144 8.2 The Category of Sheaves . 150 8.3 Sheaf Cohomology . 156 8.4 Cechˇ Cohomology . 161 8.5 Direct and Inverse Image . 170 ii 0 Introduction 0 Introduction These notes are taken from a reading course on homological algebra led by Dr.
    [Show full text]
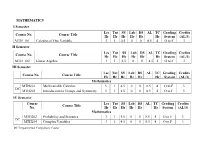
  • MATHEMATICS I Semester Course No. Course Title Lec Hr Tut Hr SS Hr Lab Hr DS Hr AL TC Hr Grading System Credits (AL/3) MTH
    MATHEMATICS I Semester Lec Tut SS Lab DS AL TC Grading Credits Course No. Course Title Hr Hr Hr Hr Hr Hr System (AL/3) MTH 101 Calculus of One Variable 3 1 4.5 0 0 8.5 4 O to F 3 II Semester Lec Tut SS Lab DS AL TC Grading Credits Course No. Course Title Hr Hr Hr Hr Hr Hr System (AL/3) MTH 102 Linear Algebra 3 1 4.5 0 0 8.5 4 O to F 3 III Semester Lec Tut SS Lab DS AL TC Grading Credits Course No. Course Title Hr Hr Hr Hr Hr Hr System (AL/3) Mathematics MTH201 Multivariable Calculus 3 1 4.5 0 0 8.5 4 O to F 3 DC MTH203 Introduction to Groups and Symmetry 3 1 4.5 0 0 8.5 4 O to F 3 IV Semester Course Lec Tut SS Lab DS AL TC Grading Credits Course Title No. Hr Hr Hr Hr Hr Hr System (AL/3) Mathematics MTH202 Probability and Statistics 3 1 4.5 0 0 8.5 4 O to F 3 DC MTH204 Complex Variables 3 1 4.5 0 0 8.5 4 O to F 3 DC: Departmental Compulsory Course V Semester Course No. Course Title Lec Tut SS Hr Lab DS AL TC Grading Credits Hr Hr Hr Hr Hr System MTH 301 Group Theory 3 0 7.5 0 0 10.5 3 O to F 4 MTH 303 Real Analysis I 3 0 7.5 0 0 10.5 3 O to F 4 MTH 305 Elementary Number Theory 3 0 7.5 0 0 10.5 3 O to F 4 MTH *** Departmental Elective I 3 0 7.5 0 0 10.5 3 O to F 4 *** *** Open Elective I 3 0 4.5/7.5 0 0 7.5/10.5 3 O to F 3/4 Total Credits 15 0 34.5/37.5 0 0 49.5/52.5 15 19/20 VI Semester Course No.
    [Show full text]