Rest Vs. Rust: the Effect of Disproportionate Time Between Rounds of a Playoff Series
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

AT&T Deepens Partnership with NBA and WNBA As the Official 5G
AT&T Deepens Partnership with NBA and WNBA as the Official 5G Innovation Partner What’s the news? AT&T* is broadening its collaborative partnership the NBA and WNBA as the Official 5G Innovation Partner of the NBA and WNBA. The partnership, which began in 2019, will continue to build fan-first experiences that enhance both the in-venue and at-home sports experience for fans. First, AT&T is exploring a series of game-changing augmented reality concepts for fans within the WNBA app. A prototype being concepted would allow WNBA fans to track their favorite teams and players, participate in a fun bracket-style game, and send or share some of their favorite milestones directly to friends, family or on social media. Looking to the future, AT&T will continue to develop future iterations and is excited to explore many more fan experiences within applications, online and other second-screen mediums to bring fans closer to their favorite games and athletes. What are people saying? Now more than ever, 5G, AR and immersive technology are playing a bigger role in sports. “Leveraging the speed, low latency, and compute power of 5G provides us the opportunity to be even more creative in how we enhance the fan experience,” said David Christopher, executive vice president and general manager, partnerships and 5G ecosystem development. “By unlocking more viewing options, next generation game replay and data, real-time social-first 3D content, and immersive player interaction, fans have the ability to tailor and view their content in unique, curated ways they couldn’t do before.” “The NBA remains focused on providing fans around the world with greater access to the game of basketball wherever they are,” said Steve Hellmuth, NBA Executive Vice President of Media Operations & Technology. -

CASE STUDY - FACILITY DEVELOPMENT AT&T Center - San Antonio, Texas
180 Tuckerton Rd, #10, Medford, NJ 08055 Ph. (609) 714-3330 www.staffordsports.com Fax. (609) 714-3335 CASE STUDY - FACILITY DEVELOPMENT AT&T Center - San Antonio, Texas YEAR OPENED 2002 ANCHOR San Antonio Spurs TENANTS (NBA): SALE Coliseum Advisory OWNERSHIP Board/Bexar Company MANAGEMENT San Antonio Spurs The AT&T Center is the premier sports and entertainment show place for the San Antonio region including Bexar County and the surrounding south Texas communities. It has a total seating capacity of 18,500 for basketball, with 18,000 for concerts, 17,000 for the Rodeo and 13,000 for hockey. The facility is designed with 56 luxury suites and 1,920 club seats, with parking for 7,000. The AT&T Center is the home of the NBA San Antonio Spurs and the San Antonio Livestock Exposition (SALE), as well as the WNBA San Antonio Silver Stars and the AHL San Antonio Rampage. INITIAL SITUATION the Spurs during discussions with both the City and County. Through long and often times tedious discussions, Stafford The City of San Antonio originally constructed the $186 million was able to negotiate various deal points, including revenue Alamodome in 1993 as a football stadium with the hopes of sharing, operational control, up-front equity payments, being awarded a NFL expansion team. When it was evident parking and ticket surcharges, in order to construct a deal San Antonio would not receive a team, the Spurs became that provided an equitable solution for both the Spurs and the the anchor tenant. However, with only 38 executive suites public entity. -

Kevin Durant's Heroics Power Warriors to Brink of NBA Crown
Friday 43 Sports Friday, June 8, 2018 Kevin Durant’s heroics power Warriors to brink of NBA crown ‘We have another opportunity today to extend the series’ CLEVELAND: Defending champion Golden definitely an assassin and that was one of those State, powered by 43 points from Kevin Durant, assassin plays right there,” James said. moved to the brink of a third NBA title in four sea- “It was like deja vu seeing that shot again,” sons Wednesday by defeating the Cleveland Cav- Cavaliers forward Kevin Love said. It was another aliers 110-102. The Warriors seized a dagger in the title hopes of James, who had 33 commanding 3-0 lead in the best-of-seven NBA points, 10 rebounds and 11 assists while Kevin Finals and by winning game four Friday would Love added 20 points and 13 rebounds for the complete the first championship series sweep Cavaliers. since Cleveland was blanked by San Antonio in “It was a big shot,” Cavaliers coach Tyronn 2007. “I don’t want to downplay anything but I Lue said. “He was four or five feet behind the don’t want to act like this is the end of the road,” (3-point) line and he raised up and made a big Durant said. “We did some things that we need to shot for them. So, you know, kind of like he did correct if we want to win the next game. I’ve just last year.” got stay locked in.” No team has ever recovered The Cavaliers had been 8-1 at home in the from a 3-0 deficit to win an NBA playoff series, playoffs with eight wins in a row since losing their but the Cavaliers made the top comeback in NBA first-round opener to Indiana. -

Dallas Mavericks (42-30) (3-3)
DALLAS MAVERICKS (42-30) (3-3) @ LA CLIPPERS (47-25) (3-3) Game #7 • Sunday, June 6, 2021 • 2:30 p.m. CT • STAPLES Center (Los Angeles, CA) • ABC • ESPN 103.3 FM • Univision 1270 THE 2020-21 DALLAS MAVERICKS PLAYOFF GUIDE IS AVAILABLE ONLINE AT MAVS.COM/PLAYOFFGUIDE • FOLLOW @MAVSPR ON TWITTER FOR STATS AND INFO 2020-21 REG. SEASON SCHEDULE PROBABLE STARTERS DATE OPPONENT SCORE RECORD PLAYER / 2020-21 POSTSEASON AVERAGES NOTES 12/23 @ Suns 102-106 L 0-1 12/25 @ Lakers 115-138 L 0-2 #10 Dorian Finney-Smith LAST GAME: 11 points (3-7 3FG, 2-2 FT), 7 rebounds, 4 assists and 2 steals 12/27 @ Clippers 124-73 W 1-2 F • 6-7 • 220 • Florida/USA • 5th Season in 42 minutes in Game 6 vs. LAC (6/4/21). NOTES: Scored a playoff career- 12/30 vs. Hornets 99-118 L 1-3 high 18 points in Game 1 at LAC (5/22/21) ... hit GW 3FG vs. WAS (5/1/21) 1/1 vs. Heat 93-83 W 2-3 GP/GS PPG RPG APG SPG BPG MPG ... DAL was 21-9 during the regular season when he scored in double figures, 1/3 @ Bulls 108-118 L 2-4 6/6 9.0 6.0 2.2 1.3 0.3 38.5 1/4 @ Rockets 113-100 W 3-4 including 3-1 when he scored 20+. 1/7 @ Nuggets 124-117* W 4-4 #6 LAST GAME: 7 points, 5 rebounds, 3 assists, 3 steals and 1 block in 31 1/9 vs. -

Mario Elie, Class Of
HALL OF FAME INDUCTEE Mario A. Elie, ‘81 Mario A. Elie grew up in Manhattan and was a parishioner of Holy Name of Jesus on W 96th St. Elie attended Power Memorial Academy where he played basketball alongside Chris Mullin under coach Steve Donohue. Elie played street ball in Central Park and other locations in New York City during the 1980s. Elie played college basketball at American International College in Springfield, MA. Elie led AIC to their conference's first NCAA Division II Tournament Quarter-Final. He did not catch on in the NBA right away. In 1986, Elie started his professional career at Killester in Ireland, where he won Player of the Year honors. He later played in the Portuguese League and then played in the World Basketball League and also in the Continental Basketball Association. Mario broke into the NBA in the 90-91 season playing for the Philadelphia 76ers on a short-term contract and then spent the rest of the season with the Golden State Warriors. In the 92-93 season he was with Portland and in 93-94 went to the Houston Rockets. Mario won two NBA Championships, first in 1994 and again in 1995. He continued with the Houston Rockets through the 97-98 season. He then signed with the San Antonio Spurs where he won his third NBA Championship in 1999. Mario’s final NBA year was 2000-01 when he was playing with the Phoenix Suns. In 2007 Mario was inducted into the New York Basketball Hall of Fame and was named one of the top ten players in Houston Rockets history. -
WWII ‘Rosie’ Calls LC Home Machinist Edna Crostic Biker Helped to Keep the Clings Home Fires Burning
A3 + PLUS >> Blueberry Festival is Saturday, Story below FOOTBALL NBA FINALS Preseason honors Steph, Lebron for Crumitie face off again See Page 2B See Page 1B THURSDAY, MAY 31, 2018 | YOUR COMMUNITY NEWSPAPER SINCE 1874 | $1.00 Lake City Reporter LAKECITYREPORTER.COM Murder suspect nabbed Wellborn woman was buried in shallow grave, reports say Gutierrez 2A SUV VS. MOTORCYCLE WWII ‘Rosie’ calls LC home Machinist Edna Crostic Biker helped to keep the clings home fires burning. By COREY ARWOOD [email protected] to life ith crystal clarity, a local WWII Navy vet- Weran recounted the after orange groves of her childhood, a pre boot-camp trip to the Statue of Liberty and watching war planes do the Banana River crash Bounce in 1944. A week from Saturday, Edna Irma Crostic will be 99 years Cops: Still critical, old. but some better. Crostic said she’s looking forward to another day of doing whatever she wants to do, By COREY ARWOOD whether that’s a car ride around [email protected] Alligator Lake, watching the world from her front porch or A motorcyclist remains in watching the news on televi- critical but stable condition COREY ARWOOD/Lake City Reporter sion. after a Monday night collision Crostic was born in 1919, while the status of the police when WWI had just ended and the face of the modern world investigation remains to be was being forged. determined as investigators Little did Crostic know her continue looking into in the own future was being shaped by crash, LCPD said. events across the Atlantic while Lake City Police Public she was at home in the orange Information Officer Mike Lee groves of St. -

Halep Fights Back to Win French Open ‘It’S a Dream and It’S So Special to Do It Here in Paris’
Established 1961 Sport SUNDAY, JUNE 10, 2018 Pocock shines as Australia Nationals lose opener to Giants as Brazil’s blind footballers see 25beat Ireland in Brisbane 26 Stephen heads for MRI on right shoulder 27 way to their own World Cup glory PARIS: Romania’s Simona Halep (2nd R), poses with her trophy next to second placed Sloane Stephens of the US (2nd L), French Tennis Federation (FFT) President Bernard Giudicelli (R) and former Spanish tennis player Arantxa S·nchez Vicario (L), after the women’s singles final match against Romania’s Simona Halep, yesterday. — AFP Halep fights back to win French Open ‘It’s a dream and it’s so special to do it here in Paris’ PARIS: Simona Halep fought back from a set and a but the American 10th seed wilted in hot conditions two big forehands left the top seed scrambling. The ear- against Ostapenko, and she broke back to love to the break down to finally achieve her “dream” of winning a and Halep pounced. “It’s been amazing here for me,” ly exchanges were brutal in the Paris heat, but it was the delight of the crowd. Grand Slam title, beating Sloane Stephens 3-6, 6-4, 6-1 said Stephens. “It’s not the trophy I wanted, but it’s world number one who found herself being forced onto Suddenly Halep had won 12 of 13 points and in a gruelling French Open final yesterday. still beautiful.” the defensive as Stephens moved 4-1 ahead. snatched the momentum, and she made it four games The world number one had lost all three of her previ- Halep played a scintillating deciding set in which she The 25-year-old, who was ranked 957 in the world on the spin as Stephens dumped consecutive forehands ous major finals, including two at Roland Garros, and made only five unforced errors, breaking her major duck less than a year ago after her injury woes, was using her into the net. -
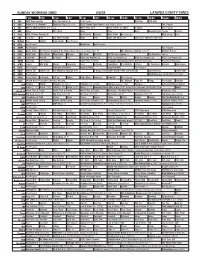
Sunday Morning Grid 6/3/18 Latimes.Com/Tv Times
SUNDAY MORNING GRID 6/3/18 LATIMES.COM/TV TIMES 7 am 7:30 8 am 8:30 9 am 9:30 10 am 10:30 11 am 11:30 12 pm 12:30 2 CBS CBS News Sunday Face the Nation (N) Paid Program Big Deal PGA Golf 4 NBC Today in L.A. Weekend Meet the Press (N) (TVG) 2018 French Open Tennis Fourth Round. (N) Å Paid Program 5 CW KTLA 5 Morning News at 7 (N) Å KTLA News at 9 KTLA 5 News at 10am In Touch Paid Program 7 ABC News This Week News News News Memorial Day Parade IndyCar 9 KCAL KCAL 9 News Sunday (N) Joel Osteen Schuller Mike Webb Paid Program REAL-Diego Paid 11 FOX In Touch Paid Fox News Sunday News Paid Tiger and Rocco (N) 2018 U.S. Women’s Open Golf 13 MyNet Paid Matter Fred Jordan Paid Program 18 KSCI Paid Program Buddhism Paid Program 22 KWHY Paid Program Paid Program 24 KVCR Burns-Story The Forever Wisdom of Dr. Wayne Dyer Tribute to Dr. Wayne Dyer. Å The Migraine Solution (TVG) Å Memory Rescue 28 KCET Zula Patrol Zula Patrol Mixed Nutz Edisons Kid Stew Biz Kid$ JFK The Last Speech Å The Wrecking Crew Å 30 ION Jeremiah Youseff In Touch Paid NCIS: Los Angeles Å NCIS: Los Angeles Å NCIS: Los Angeles Å NCIS: Los Angeles Å 34 KMEX Conexión Paid Program Como Dice el Dicho El Coyote Emplumado (1983) María Elena Velasco. República Deportiva 40 KTBN James Win Walk Prince Carpenter Jesse In Touch PowerPoint It Is Written Jeffress K. -

TEXAS LOTTERY LAUNCHES SAN ANTONIO SPURS SCRATCH TICKET New Game Offers Chance to Win a Trip for Two to the NBA All-Star 2018
FOR IMMEDIATE RELEASE MEDIA CONTACT: Media Relations, 512-344-5131 [email protected] TEXAS LOTTERY LAUNCHES SAN ANTONIO SPURS SCRATCH TICKET New game offers chance to win a trip for two to the NBA All-Star 2018 (AUSTIN) – The Texas Lottery has partnered with the San Antonio Spurs to bring basketball fans a new $5 scratch ticket that offers more than $10.2 million in total prizes, three top prizes of $100,000 and a chance to win a trip for two to the NBA All-Star 2018. The scratch ticket is available now at licensed Texas Lottery® retail locations. “We are excited to partner with the San Antonio Spurs to offer a scratch ticket game that is sure to be a slam dunk for our players,” said Gary Grief, executive director of the Texas Lottery. “The assist the Texas Lottery provides to public education and veteran’s assistance is a guaranteed winner and we’re thrilled to support their mission,” said Jeanne Garza, senior director of marketing partnerships for Spurs Sports & Entertainment. Players that do not win instantly can enter non-winning tickets into one of four promotional second-chance drawings. One lucky winner per drawing will win a trip for two to the NBA All-Star 2018. Trip for two to the NBA All-Star 2018 includes: Round-trip coach airfare for two in the continental United States to Los Angeles, California One standard hotel room for three nights $1,000 spending money Ground transportation to and from the airport and hotel Two tickets to the NBA All-Star Saturday Night 2018 and the 2018 NBA All-Star Game One merchandise prize pack In addition to the NBA All-Star 2018 trip prizes, 242 San Antonio Spurs merchandise prize packs, each valued at $595, will be given away per drawing. -

CHARLIE AMATO Chairman and Co-Founder of SWBC
866.498.3441 [email protected] CHARLIE AMATO Chairman and Co-founder of SWBC EDUCATION Charlie Amato is the Chairman of SWBC. With more than 40 years of experience in all aspects of insurance operations, underwriting, and Sam Houston State University product development. Charlie is known in the business community Bachelor of Business Administration for his innovative, relationship-building approach. APPOINTMENTS: EXPERIENCE • Regent, Texas State University System (2012 Chairman) 40+ years • Board Member, Federal Reserve Bank of Dallas, San Antonio Branch RECOGNITIONS AFFILIATIONS: • 2018 Richard W. Weekley Public Policy • Investor, San Antonio Spurs Leadership Award from the Texas • Chairman, Texas State University System Foundation Business Leadership Council • Board Member, Lone Star Capital Bank • 2018 Legacy Leaders Award from the San • National Director, Sigma Phi Epsilon Fraternity Antonio Business Journal • Vice Chairman, Texas Business Leadership Council • 2017 Impact Award from Sam Houston State University Sport Management • Board Member, CHRISTUS Santa Rosa Children’s Hospital Foundation Industry • Board Member, Silver and Black Give Back • 2016 Pathfinder Award from the • Board Member, Botanical Research Institute of Texas San Antonio Chamber of Commerce • Board Member, Greater San Antonio Chamber of Commerce; • 2016 Doctor of Humane Letters degree 2000 Chairman from the University of Incarnate Word • Board Member, USLD Communications, 1992–1997 • 2016 Icons in Healthcare Honoree— • Member, InfraGard; Vice President, 2009–2011 CentroMed -

Simona Halep Kisses the Trophy As She Celebrates After Winning the French Open Final Against Sloane Stephens of the US Yesterday
FOOTBALL | Page 3 NBA | Page 5 Sterling Warriors relishes sweep aside World Cavaliers to Cup stage claim title Sunday, June 10, 2018 TENNIS Ramadan 25, 1439 AH Nadal chases GULF TIMES 11th French Open crown SPORT Page 2 TENNIS/FRENCH OPEN Thrilling fi ghtback gives Halep fi rst Grand Slam title ‘In the last game I felt like I could not breathe anymore’ ATHLETICS Qatar’s Saife bags his second gold medal at Asian Juniors By Sports Reporter to his personal tally yesterday. Gifu, Japan His throw of 61.50m in the discus was well short of Iran’s Hossein Rasouli’s 62.29m. Japan’s Kosei Yamashita was atar’s rising middle distance a distant third with a heave of 56.51m. runner Saife Saifeldin claimed Huanhuan Yang of China won the gold his second gold medal of the medal in the women discus throw with Asian Junior Athletics Cham- a throw of 51.53m while her teammate Qpionships in Japan when he surged to Yuanyuan Yin secured silver medal with victory in the 3,000m steeplechase at the 51.17m and India’s Arpandeep Kaur Bajwa Nagaragawa Stadium in Gifu yesterday. took bronze medal in 46.57m. Saifeldin clocked 8mins 51.97secs to Ayaka Kora of Japan and Jiawei Zhong comfortably beat silver medallist Takumi of China were locked in the most thrill- Yoshida of Japan (8:52.79) and Trung ing women’s long jump fi nal when both Cuong Nguyen of Vietnam (8:59.32) cleared 6.44m in their 5th attempt to tie. His victory yesterday took Qatar’s gold Kora, riding on home support leapt 1cm medal tally to three after he and Ibrahim more than Jiawei in the fi nal jump to break Moaaz Mohamed had won the 1,500m the tie and win the gold medal. -

Thunder Guide 2018 R110518.Pdf
TABLE OF CONTENTS GENERAL INFORMATION ALL-TIME RECORDS General Information ....................................................................................4 Year-By-Year Record .............................................................................119 All-Time Coaching Records ....................................................................120 THUNDER OWNERSHIP GROUP Opening Night .........................................................................................121 Clayton I. Bennett .......................................................................................7 All-Time Opening-Night Starting Lineups ...............................................122 Board of Directors .......................................................................................7 High-Low Scoring Games/Win-Loss Streaks .........................................122 All-Time Winning-Losing Streaks/Win-Loss Margins ..............................124 PLAYERS Overtime Results ....................................................................................125 Photo Roster .............................................................................................10 Team Records ........................................................................................127 Roster .......................................................................................................11 Opponent Team Records .......................................................................128 Alex Abrines .............................................................................................12