An Exploratory Analysis
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Oversigt Over Retskredsnumre
Oversigt over retskredsnumre I forbindelse med retskredsreformen, der trådte i kraft den 1. januar 2007, ændredes retskredsenes numre. Retskredsnummeret er det samme som myndighedskoden på www.tinglysning.dk. De nye retskredsnumre er følgende: Retskreds nr. 1 – Retten i Hjørring Retskreds nr. 2 – Retten i Aalborg Retskreds nr. 3 – Retten i Randers Retskreds nr. 4 – Retten i Aarhus Retskreds nr. 5 – Retten i Viborg Retskreds nr. 6 – Retten i Holstebro Retskreds nr. 7 – Retten i Herning Retskreds nr. 8 – Retten i Horsens Retskreds nr. 9 – Retten i Kolding Retskreds nr. 10 – Retten i Esbjerg Retskreds nr. 11 – Retten i Sønderborg Retskreds nr. 12 – Retten i Odense Retskreds nr. 13 – Retten i Svendborg Retskreds nr. 14 – Retten i Nykøbing Falster Retskreds nr. 15 – Retten i Næstved Retskreds nr. 16 – Retten i Holbæk Retskreds nr. 17 – Retten i Roskilde Retskreds nr. 18 – Retten i Hillerød Retskreds nr. 19 – Retten i Helsingør Retskreds nr. 20 – Retten i Lyngby Retskreds nr. 21 – Retten i Glostrup Retskreds nr. 22 – Retten på Frederiksberg Retskreds nr. 23 – Københavns Byret Retskreds nr. 24 – Retten på Bornholm Indtil 1. januar 2007 havde retskredsene følende numre: Retskreds nr. 1 – Københavns Byret Retskreds nr. 2 – Retten på Frederiksberg Retskreds nr. 3 – Retten i Gentofte Retskreds nr. 4 – Retten i Lyngby Retskreds nr. 5 – Retten i Gladsaxe Retskreds nr. 6 – Retten i Ballerup Retskreds nr. 7 – Retten i Hvidovre Retskreds nr. 8 – Retten i Rødovre Retskreds nr. 9 – Retten i Glostrup Retskreds nr. 10 – Retten i Brøndbyerne Retskreds nr. 11 – Retten i Taastrup Retskreds nr. 12 – Retten i Tårnby Retskreds nr. 13 – Retten i Helsingør Retskreds nr. -

Danske Borgmestre 1970-2018
Danske borgmestre 1970-2018 Ulrik Kjær Niels Opstrup Kommunalpolitiske Studier Nr. 33/2018 Danske borgmestre 1970- 2018 Borgmesterarkivet rummer oplysninger om samtlige 1380 personer, der har siddet som borgmester i en dansk kommune efter kommunalvalget den 3. marts 1970 til og med den 1. januar 2018, hvor seneste valgperiode begynde. Første runde af oplysninger blev indsamlet i efteråret 2004. Samtlige af de daværende 271 kommuner modtag ultimo august 2004 et kort spørgeskema, hvori de blev bedt om at anføre kommunens borgmestre i perioden 1970-2004, samt angive nogle få supplerende oplysninger (såsom borgmestrenes fødselsår, deres erhvervsbaggrund og årsagen til at de forlod posten). I praksis foregik indsamlingen ved, at der på baggrund af oplysninger fra nyhedsmagasinet Danske Kommuner blev udfærdiget en oversigt over borgmestrene, som den enkelte kommune så blev bedt om at verificere eller rette i, samt tilføje de ekstra oplysninger, de blev bedt om. Fire kommuner svarede ikke på henvendelsen, hvorfor oplysninger om borgmestre fra disse stammer fra søgninger i aviser og lokale dagblade (se Rikke Berg & Ulrik Kjær: ”Den danske borgmester”, Syddansk Universitetsforlag, 2004). I efteråret 2011 blev der gangsat endnu en dataindsamlingsrunde. Pr. mail blev der rettet henvendelse til 29 kommuner og/ eller lokalhistoriske arkiver med henblik på at indhente baggrundsoplysninger om en række borgmestre, hvor disse manglede. Borgmesterarkivet er desuden siden 2004 løbende blev opdateret ved skift på borgmesterposterne på baggrund oplysninger -

Falck Healthcare Sundhedscentre I Danmark
Falck Healthcare Sundhedscentre i Danmark Bemærk: Nogle sundhedscentre tilbyder ikke alle fire behandlingsformer. Der kan bookes Sundhedsprofil på visse sundhedscentre. Kiropraktisk Klinik Rødovre Fitness Club Højbro Plads, St. Kirkestræde 3, 1. Tæbyvej 7 1073 København K 2610 Rødovre Gothersgade Sundhedscenter Kiropraktorhuset Gothersgade 153, kl. tv. Taastrup Hovedgade 41, st. th. 1123 København K 2630 Taastrup Kiropraktisk klinik Hvidovre Scandic Hotel Borgergade 34, st. th. Kettevej 4 1300 København K 2650 Hvidovre Kiropraktisk klinik Kiropraktisk Klinik v. Helle Jørgensen Banegårdspladsen 1, 4. sal Over Bølgen 2B, 2 1570 København V 2670 Greve København V 3F Min-behandler Nyropsgade 22 Ræveholmsvej 57,1 1602 København V 2690 Karlslunde Falck Healthcare Kiropraktisk Klinik Nyropsgade 17 Frederikssundsvej 207, st. 1602 København V 2700 Brønshøj Kiropraktisk klinik Efficax Gl. Kongevej 25, 1.tv Jyllingevej 55, st. th. 1610 København V 2720 Vanløse Kiropraktisk klinik Ballerup Kiropraktor Skt. Nikolaj Vej 1 Centrumgaden 27, 1 1953 Frederiksberg 2750 Ballerup Kiropraktisk klinik Kiropraktisk Klinik Godthåbsvej 129, st. tv Centrumgaden 24, 1. mf. 2000 Frederiksberg 2750 Ballerup Kiropraktisk Klinik Kiropraktisk Klinik Tårnby ApS Nyelandsvej 2B, st. Kamillevej 4 2000 Frederiksberg 2770 Kastrup Falck Healthcare Østerbro Lyngby Kiropraktik J.E. Ohlsensgade 2, 1. th Lyngby Hovedgade 27-29 2100 København Ø 2800 Kgs. Lyngby Kiropraktorerne - Islands Brygge Vangede Kiropraktik & Sundhed ApS Islands Brygge 17, st. th. v. Lærke Enggaard Jensen 2300 -

EGOS Full Paper LF
Roskilde University The sense of services in a globalizing public sector Fuglsang, Lars Publication date: 2010 Citation for published version (APA): Fuglsang, L. (2010). The sense of services in a globalizing public sector. Paper presented at 26th EGOS Colloquium, Lisabon, Portugal. General rights Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from the public portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain. • You may freely distribute the URL identifying the publication in the public portal. Take down policy If you believe that this document breaches copyright please contact [email protected] providing details, and we will remove access to the work immediately and investigate your claim. Download date: 01. Oct. 2021 The sense of services in a globalizing public sector Lars Fuglsang, Roskilde University Work in progress Prepared for Sub-theme 06 (SWG): Assembling Global and Local: Practice-Based Studies of Globalization in Organization, 26th EGOS Colloquium, Lisbon, June 28-July 3. Convenors: Paolo Landri, Bente Elkjaer, Silvia Gherardi. Abstract. This paper represents an attempt to explore in a qualitative way how the microstructure of public private innovation networks in public services (ServPPINs) can be understood. The paper uses the concepts of sensemaking and weak cues from the sensemaking literature to explain how these ServPPINs manage to take care of development and change (Weick 1979, 1995). -

Samlede SM-Resultater
Sjællandske Mesterskaber 12/8 m. 2005 Resultatliste Herre Micro Compound 01. Thomas Jensen Taastrup 282 285 567 02. Stephan Hansen Nykøbing F. 272 278 550 03. Nikolai Pedersen Helsinge 246 253 499 04. Sebastian Sørensen Helsinge 173 180 353 05. Peder Sigil Vordingborg 0 0 0 06. Sylvester Pedersen Nykøbing F. 0 0 0 07. Silas Pedersen Nykøbing F. 0 0 0 08. Tobias Hansen Nykøbing F. 0 0 0 Herre Micro Recurve. 01. Frederik Wissum Nivå 270 271 541 02. Adam Palmar Lavia K. 261 267 528 03. Christian Larsen Vordingborg 234 261 495 04. Casper Thøstesen Nordkysten 239 230 469 05. Lau Jørgensen Nordkysten 224 205 429 06. Niclas Friese Nordkysten 217 173 390 07. Casper R. Lauridsen Hillerød 176 204 380 08. Tobias Berg Colten Hillerød 205 157 362 09. Benjamin Knudsen Nordkysten 182 166 348 10. Andreas Rasmussen Køge 0 0 0 Dame Micro Recurve. 01. Cecilie Christoffersen Nordkysten 82 65 147 Herre Micro Barbue. 01. Thomas Dumong Roskilde 174 190 364 02. Anders Johansen Helsinge 151 143 294 03. Henrik Borer Lyngby 139 146 285 04. Tim Rubeksen Helsinge 117 124 241 05. Simon Rubeksen Helsinge 79 45 124 06. Pelle Skar Køge 0 0 0 Dame Micro Barbue. 01 Matilde Johansen. Helsinge 6 16 22 Herre Micro Langbue. 01. Laust Andersen København 187 221 408 02. Emil Sørensen København 204 159 363 Herre Mini Compound. 01. Mads Knudsen Nordkysten 285 272 557 02. Torben Nørgaard Gladsaxe 271 268 539 03. Dennis Vejlin Taastrup 268 261 529 04. Simon Sørensen Helsinge 250 245 495 05. -
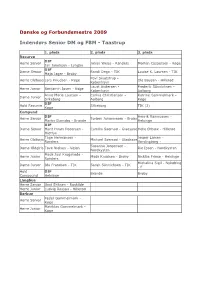
2009 Danske Og Forbundsmestre
Danske og Forbundsmestre 2009 Indendørs Senior DM og FBM - Taastrup 1. plads 2. plads 3. plads Recurve DIF Herre Senior Johan Weiss - Randers Morten Caspersen - Køge Jan Jakobsen - Lyngby DIF Dame Senior Randi Degn - TIK Louise K. Laursen - TIK Maja Jager - Broby Povl Skudstrup - Herre Oldboys Lars Knudsen - Køge Ole Boysen - Hillerød København Laust Andersen - Frederik Sönnichsen - Herre Junior Benjamin Ipsen - Køge København Aalborg Anne Marie Laursen - Carina Christiansen - Katrine Gammelmark - Dame Junior Silkeborg Aalborg Køge DIF Hold Recurve Silkeborg TIK (2) Køge Compund DIF Henrik Rasmussen - Herre Senior Torben Johannesen - Broby Martin Damsbo - Brande Helsinge DIF Dame Senior Marit Hvam Pedersen - Camilla Søemod - Gladsaxe Helle Ørbæk - Hillerød Midtfyn Tage Hermansen - Jesper Larsen - Herre Oldboys Michael Søemod - Gladsaxe Randers Vordingborg - Susanne Jørgensen - Dame Oldgirls Tove Nielsen - Vejen Rie Ipsen - Nordkysten Nordkysten Mads Juul Krogshede - Herre Junior Mads Knudsen - Broby Nicklas Friese - Helsinge Randers Michalina Sigil - Nykøbing Dame Junior Ida Frandsen - TIK Sarah Sönnichsen - TIK - F Hold DIF Brande Broby Compound Helsinge Langbue Herre Senior Unni Eriksen - Roskilde Herre Junior Ludvig Rossau - Hillerød Barbue Peder Gammelmark - Herre Senior Køge Matthias Gammelmark - Herre Junior Køge Indendørs Ungdoms FBM - Middelfart 1. plads 2. plads 3. plads Recurve Herre Laust Andersen - Jacob Isager Troelsen - Mathias Galberg - Aalborg Kadet København Hillerød Dame Anne Marie Laursen - Nynne Holdt-Caspersen - Tanya -

Amateur Radio Award's Directory Denmark .1
AAMMAATTEEUURR RRAADDIIOO AAWWAARRDD’’’SS DDIIRREECCTTOORRYY DENMARK COPYED BY : YB1PR – FAISAL Page 1 . EXPERIMENTERENDE DANSKE RADIOAMATORER SERIES General Requirements: Fee is shown for each award. GCR list to Award Manager, Allis Andersen OZ1ACB, Kagsaavej 34, DK-2730 Herlev, Denmark. Cross Country Award Contact OZ and OX prefixes since 1 Apr 1970. Available all cw or all phone. Point requirements: Scandanavian stations: Class 1 = 70 points in all communities plus OX3. Class 2 = 50 points in at least 10 counties. Other Europeans = 50 points. All others = 40 points. Points are earned as follows: 1. Scandanavian: 80 to 2 meters = 1 pt. 432 MHz contacts = 2 pts. 3 stations must be contacted in each county on 80 and 40. 4 stations must be contacted in each county on 20, 15, 10 and 2. 5 stations may be contacted in each county on 70cm. 2. Other Europeans (contact OZ call areas): Each prefix 0Z1 to OZ9 and OX3 MUST be contacted. 2 contacts with each prefix permitted on each band except OX3 where 9 are permitted on each band. Each contact = 1 point except 70cm = 2 points. 3. All others - (contact OZ call areas): Each prefix OZ1 to OZ9 and OX3 must be contacted. 3 contacts with each prefix permitted on each band except OX3 where 9 are permitted on each band. Contact points as above. Counties in Denmark: 1. Koebenhavns amt (IOTA EU-029) 2. Frederiksborg amt (IOTA EU029) 3. Roskilde amt (IOTA EU-029) 4. Vestsjaellands amt (IOTA EU-029) 5. Storstroems amt (IOTA EU-029) 6. Bornholms amt (IOTA EU030) 7. -

Denmark Atlas
FF II CC SS SS Field Information and Coordination Support Section Division of Operational Services Denmark Sources: UNHCR, Global Insight digital mapping © 1998 Europa Technologies Ltd. As of December 2009 The boundaries and names shown and the designations used on this map do not imply official endorsement or acceptance by the United Nations. Name_of_the_workspace.WOR ((( Rångedala !! Ulriceham !! Lerum !! !! !! Skagen ((( Hindås !! Borås ((( Hönö !! ((( !! Göteborg ((( Vegby ((( Bollebygd ((( Kandesterne !! ((( ((( Viskafors ((( Hillared ((( ((( ((( ((( Hirtshals ((( Tversted ((( Askim((( Billdal ((( Hyssna ((( Fritsla ((( !! Jerup ((( Limmared North Sea !! !! Kungsbacka !! ((( Kinna ((( Tranemo((( Hestra ((( Lonstrup !! Hjorring !! Frederikshavn ((( ((( Onsala SWEDEN((( ((( Saeby ((( ((( ((( Ingstrup Frillesås ((( ((( ((( ((( A ((( ((( Dybvad ((( Vestero Havn !! Bronderslev ((( ((( ((( ((( Blokhus ((( ((( Burseryd ((( ((( ((( Hjallerup((( ((( Smålandsste ((( ((( ((( ((( Lild Strand Nørre Halne ((( Asa ((( Ullared ((( ((( Hanstholm ((( Ätran ((( !! ((( ((( Vodskov !! Varberg ((( ((( Brovst ((( ((( Fjerritslev Frøstrup ((( Landeryd !! ((( ((( Klitmoller ((( !! ((( Osterild !! ÅlborgAalborg Danish Straits ((( ((( Hals ((( Vessigebro ((( ((( Nibe ((( ((( Svenstrup((( ((( ((( ((( ((( Logstor Gudumholm ((( Unnary ((( Norre Vorupor((( !! Thisted ((( ((( Snedsted((( Stovring !! ((( ((( Sonder Dråby ((( !! Falkenberg ((( ((( ((( ((( Lidhult ((( Terndrup Getinge ((( Ars !! Nykobing ((( ((( Farso ((( Arden ((( ((( ((( ((( ((( ((( ((( Als ((( -

Supplementary to ``Eliciting Risk and Time Preferences''
Econometrica Supplementary Material SUPPLEMENTARY TO “ELICITING RISK AND TIME PREFERENCES” (Econometrica, Vol. 76, No. 3, May 2008, 583–618) BY STEFFEN ANDERSEN,GLENN W. H ARRISON,W.HARRISON, MORTEN I. LAU, AND E. ELISABET RUTSTRÖM Table of Contents Appendix A: Questionnaires . .......................................1 A.1 Part I of the Experiment: Socio-Demographic Questionnaire. .1 A.2QuestionnaireAboutPlansWithMoneyinIDRPart..............4 A.3PartIVoftheExperiment:QuestionnaireAboutFinances.........4 Appendix B: Sample Design . ..........................................14 B.1OverallDesign..................................................14 B.2ListofDanishMunicipalitiesandCountyCodes..................15 B.3MapofDenmark...............................................22 B.4RecruitmentProcedures.........................................23 B.5LettersofInvitationandCorrespondence........................27 Appendix C: Experimenter Script . .....................................30 Appendix D: Data and Statistical Analysis . ............................45 Appendix E: Theoretical Notes . ....................................46 APPENDIX A: QUESTIONNAIRES This appendix presents the survey questions asked of subjects in Parts I and IV of the experiment, as well as the data coding for responses. These are all translations of the original Danish, available on request. A.1. Part I of the Experiment: Socio-Demographic Questionnaire In this survey most of the questions asked are descriptive. The questions may seem personal, but they will help us analyze -

Danske Og Forbundsmestre 2012
Danske og Forbundsmestre 2012 DM og FBM 3D - Nørre Snede 15.- 16. september 2012 1. plads 2. plads 3. plads Recurve Herre Senior Daniel C. Jensen - Viking Dennis Bager - Arcus Hans Madsen - Fredericia Herre FITA Thomas Weltz - Viking Jonas Ishøj Nielsen - Lyngby Kadet Herre Kadet Magnus Bager - Arcus Dame Mini Freja Dam - Sorø Herre Micro Mark Haubjerg Pedersen - Brande Mark Drachmann - Viking Compound Herre Senior DIF - Stig Andersen - Middelfart Flemming Knudsen - Broby Helge Brummer - Christiansfeld Herre Master Andreas Clausen - Nr. Snede Bo Nielsen - Nr. Snede Arne Nielsen - Vejen Dame Master Tove Nielsen - Vejen Herre FITA Roar Brummer - Christiansfeld Mads Rømer Møller - Palnatoke Junior Dame FITA Malou Petersen - Nr. Snede Astrid Krag Kirkeby - Herning Junior Herre FITA Rene Vissing Kristiansen - Anders Djernæs Bech - Jens Jørgensen - Sorø Kadet Christiansfeld Haderslev Herre Kadet Jens Teuchler - Ribe Ivan Rasmussen - Helsinge Thor Kamp Opstrup - Ulbølle Herre Mini Marcus Sehested - Vordingborg Marc Petersen - Nr. Snede Lasse Helgesen - Broby Dame Micro Sasha Haagen Andersen - Lyngby Hold 45 m hold Nr. Snede (Bo, Peder, Andreas) Nr. Snede (Adrian, Michael, Erik) Ribe (Claus, Jan, Jens Erik) Kadet hold Ribe (Jens, Christoffer, Rune) Barbue DIF - Jens Otto Håkonson - Herre Senior Claus K. V. Larsen - København Tonny Lindahl - Haderslev Frederiksværk Herre Master Erik Profitlich - Frederiksværk John Hansen - Sorø Henning K. Jensen - Haderslev Dame FITA Malou Engelbrecht - Haderslev Victoria Skjemstad - Haderslev Kadet Herre Kadet Lars Birch Jensen - Haderslev Dame Kadet Iben Birk Jensen - Haderslev Dannie Storm Pedersen - Herre Mini Thor Borne - Helsinge Nicklas Skjemstad - Haderslev Favrskov Dame Micro Victoria Mejer-Larsen - Sorø Hold 30 m hold Haderslev (Malou, Victoria, Tonny) Langbue Bjarke B. -

100 Percent Made to Feel Good Customer List DK.Xlsx
Company Name Post Address Post Zip City AAV DÆK ÅRHUS A/S SINTRUPVEJ 40 8220 BRABRAND AAV DÆK HERNING A/S SANDAGERVEJ 31 7400 HERNING AAV DÆK ÅLBORG FÅBORGVEJ 11 9220 ÅLBORG ØST ALCAR DANMARK A/S BIZONVEJ SKOVSBY 2 A 8464 GALTEN ALS DÆKSERVICE SJÆLLANDSGADE 2 6400 SØNDERBORG AN BILER AALBORGVEJ 23 9575 TERNDRUP A.P. HELLISEN A/S RØNNEVEL 90 3720 ÅKIRKEBY AU2PARTS HADERSLEV NORGESVEJ 14 6100 HADERSLEV AULUM AUTO TEKNIK DREJERVEJ 22 7490 AULUM AUTO EXPERTEN V/ LASSE G HANSEN HÅNDVÆRKERVÆNGET 9 2670 GREVE AUTO-G RANDERS A/S ØRNEBORGVEJ 19 8960 RANDERS SØ AUTOMECCANICA ENERGIVEJ 1 4180 SORØ AUTOCARE ANTIRUST APS RUGVÆNGET 11A 2630 TÅSTRUP AUTOGÅRDEN VIDEBÆK A/S NYGADE 21 6920 VIDEBÆK AVEDØRE DÆKSERVICE KANALHOLMEN 2 2650 HVIDOVRE BARGIB AUTOGUMMI A/S ÅDALSVEJ 50 2970 HØRSHOLM BENT RASMUSSEN AUTODELE A/S SKELLET 25 4700 NÆSTVED BENT RASMUSSEN AUTODELE A/S MARIENBERGVEJ 111A 4760 VORDINGBORG BILCENTRET A.NIELSEN AS MANDAL ALLÉ 15 5500 MIDDELFART POINT S FÆRØERNE P.O Box 1234 110 TORSHAVN BIRI DRIVE IN CENTER A/S BREGNERØDVEJ 136 3460 BIRKERØD BLOHMS EFTF. DÆK OG FÆLGE APS DAMSGÅRDVEJ 11 5540 ULLERSLEV BØRGE PEDERSEN AUTOMOBILER A/S MARINEBUEN 1B 4700 NÆSTVED BØTTCHER & GAARDSØE A/S FREDERIKSVÆRKVEJ 28 3600 FREDERIKSSUND BØTTCHER & GAARDSØE HELSINGE A/S TOFTE INDUSTRI 17 3200 HELSINGE CAR-TEAM I/S NORGESVEJ 8 8450 HAMMEL CAR-DÆK A/S INDUSTRIVÆNGET 23 4622 HAVDRUP CARLO´S VULKANISERING A/S ELMEGADE 21 4400 KALUNDBORG CS BILER MARKEDSVEJ 15 9600 AARS D.K. AUTOSERVICE GRUNDTVIGSVEJ ELLING 78 9900 FREDERIKSHAVN D.V.I. DÆKCENTER GRYNDERUPVEJEN 6 9610 NØRAGER DÆK & POT MARKVÆNGET 28 9600 AARS DÆK & HAVEBUTIKKEN OLSTRUPVEJ 1 4684 HOLME-OLSTRUP DÆKCENTRALEN RAASIGVANGEN 5 3550 SLANGERUP DÆKRINGEN VORDINGBORG APS TANDHJULET 4 4760 VORDINGBORG DÆKBUTIKKEN NORDSTJERNEVEJ 1 9440 ÅBYBRO E.LARSEN & SØNNER I/S RINGSTEDVEJ 16 4520 SVINNINGE EUROMASTER PARTNER ALLERØD GYDEVANG 2-4 3450 ALLERØD EUROMASTER BRANDE VESTERGÅRDSVEJ 11 7330 BRANDE EUROMASTER BRØNDBY NYAGER 8-16 2605 BRØNDBY EUROMASTER ESBJERG D. -

Wastewater Lagoons & Odour Control
BRAZEAU COUNTY COUNCIL MEETING October 3, 2017 VISION: Brazeau County fosters RURAL VALUES, INNOVATION, CREATIVITY, LEADERSHIP and is a place where a DIVERSE ECONOMY offers QUALITY OF LIFE for our citizens. MISSION: A spirit of community created through INNOVATION and OPPORTUNITIES GOALS 1) Brazeau County collaboration with Canadians has created economic opportunity and prosperity for our community. That we intentionally, proactively network with Canadians to bring ideas and initiative back to our citizens. 2) Brazeau County has promoted and invested in innovation offering incentives diversifying our local economy, rural values and through opportunities reducing our environmental impact. Invest in green energy programs, water and waste water upgrades, encourage, support, innovation and economic growth through complied LUB, promoting sustaining small farms, hamlet investment/redevelopment. 3) Brazeau County is strategically assigning financial and physical resources to meet ongoing service delivery to ensure the success of our greater community. Rigorous budget and restrictive surplus process, petition for government funding, balance budget with department goals and objectives. 4) Brazeau County has a land use bylaw and framework that consistently guides development and promotes growth. Promotes development of business that is consistent for all “open for business.” Attract and retain businesses because we have flexibility within our planning documents. 5) Come to Brazeau County to work, rest and play. This encompasses all families. We have the diversity to attract people for the work opportunities. We have recreation which promotes rest and play possibilities that are endless. 6) Brazeau County is responsive to its citizenship needs and our citizens are engaged in initiatives. Engage in various levels - website, Facebook, newspapers, open houses.