Time Crystals
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
Time Quasilattices in Dissipative Dynamical Systems Abstract Contents
SciPost Phys. 5, 001 (2018) Time quasilattices in dissipative dynamical systems Felix Flicker1,2 1 Rudolph Peierls Centre for Theoretical Physics, University of Oxford, Department of Physics, Clarendon Laboratory, Parks Road, Oxford, OX1 3PU, UK 2 Department of Physics, University of California, Berkeley, California 94720 USA fl[email protected] Abstract We establish the existence of ‘time quasilattices’ as stable trajectories in dissipative dy- namical systems. These tilings of the time axis, with two unit cells of different durations, can be generated as cuts through a periodic lattice spanned by two orthogonal directions of time. We show that there are precisely two admissible time quasilattices, which we term the infinite Pell and Clapeyron words, reached by a generalization of the period- doubling cascade. Finite Pell and Clapeyron words of increasing length provide system- atic periodic approximations to time quasilattices which can be verified experimentally. The results apply to all systems featuring the universal sequence of periodic windows. We provide examples of discrete-time maps, and periodically-driven continuous-time dy- namical systems. We identify quantum many-body systems in which time quasilattices develop rigidity via the interaction of many degrees of freedom, thus constituting dissi- pative discrete ‘time quasicrystals’. Copyright F. Flicker. Received 30-10-2017 This work is licensed under the Creative Commons Accepted 15-06-2018 Check for Attribution 4.0 International License. Published 03-07-2018 updates Published -
![Arxiv:2005.03138V2 [Cond-Mat.Quant-Gas] 23 May 2020 Contents](https://docslib.b-cdn.net/cover/8131/arxiv-2005-03138v2-cond-mat-quant-gas-23-may-2020-contents-58131.webp)
Arxiv:2005.03138V2 [Cond-Mat.Quant-Gas] 23 May 2020 Contents
Condensed Matter Physics in Time Crystals Lingzhen Guo1 and Pengfei Liang2;3 1Max Planck Institute for the Science of Light (MPL), Staudtstrasse 2, 91058 Erlangen, Germany 2Beijing Computational Science Research Center, 100193 Beijing, China 3Abdus Salam ICTP, Strada Costiera 11, I-34151 Trieste, Italy E-mail: [email protected] Abstract. Time crystals are physical systems whose time translation symmetry is spontaneously broken. Although the spontaneous breaking of continuous time- translation symmetry in static systems is proved impossible for the equilibrium state, the discrete time-translation symmetry in periodically driven (Floquet) systems is allowed to be spontaneously broken, resulting in the so-called Floquet or discrete time crystals. While most works so far searching for time crystals focus on the symmetry breaking process and the possible stabilising mechanisms, the many-body physics from the interplay of symmetry-broken states, which we call the condensed matter physics in time crystals, is not fully explored yet. This review aims to summarise the very preliminary results in this new research field with an analogous structure of condensed matter theory in solids. The whole theory is built on a hidden symmetry in time crystals, i.e., the phase space lattice symmetry, which allows us to develop the band theory, topology and strongly correlated models in phase space lattice. In the end, we outline the possible topics and directions for the future research. arXiv:2005.03138v2 [cond-mat.quant-gas] 23 May 2020 Contents 1 Brief introduction to time crystals3 1.1 Wilczek's time crystal . .3 1.2 No-go theorem . .3 1.3 Discrete time-translation symmetry breaking . -

Creating Big Time Crystals with Ultracold Atoms
New J. Phys. 22 (2020) 085004 https://doi.org/10.1088/1367-2630/aba3e6 PAPER Creating big time crystals with ultracold atoms OPEN ACCESS Krzysztof Giergiel1,TienTran2, Ali Zaheer2,ArpanaSingh2,AndreiSidorov2,Krzysztof RECEIVED 1 2 1 April 2020 Sacha and Peter Hannaford 1 Instytut Fizyki Teoretycznej, Universytet Jagiellonski, ulica Profesora Stanislawa Lojasiewicza 11, PL-30-348 Krakow, Poland REVISED 2 23 June 2020 Optical Sciences Centre, Swinburne University of Technology, Hawthorn, Victoria 3122, Australia ACCEPTED FOR PUBLICATION E-mail: [email protected] and [email protected] 8 July 2020 PUBLISHED Keywords: time crystals, Bose–Einstein condensate, ultracold atoms 17 August 2020 Original content from Abstract this work may be used under the terms of the We investigate the size of discrete time crystals s (ratio of response period to driving period) that Creative Commons Attribution 4.0 licence. can be created for a Bose–Einstein condensate (BEC) bouncing resonantly on an oscillating Any further distribution mirror. We find that time crystals can be created with sizes in the range s ≈ 20–100 and that such of this work must maintain attribution to big time crystals are easier to realize experimentally than a period-doubling (s=2) time crystal the author(s) and the because they require either a larger drop height or a smaller number of bounces on the mirror. We title of the work, journal citation and DOI. also investigate the effects of having a realistic soft Gaussian potential mirror for the bouncing BEC, such as that produced by a repulsive light-sheet, which is found to make the experiment easier to implement than a hard-wall potential mirror. -

Solid State Physics II Level 4 Semester 1 Course Content
Solid State Physics II Level 4 Semester 1 Course Content L1. Introduction to solid state physics - The free electron theory : Free levels in one dimension. L2. Free electron gas in three dimensions. L3. Electrical conductivity – Motion in magnetic field- Wiedemann-Franz law. L4. Nearly free electron model - origin of the energy band. L5. Bloch functions - Kronig Penney model. L6. Dielectrics I : Polarization in dielectrics L7 .Dielectrics II: Types of polarization - dielectric constant L8. Assessment L9. Experimental determination of dielectric constant L10. Ferroelectrics (1) : Ferroelectric crystals L11. Ferroelectrics (2): Piezoelectricity L12. Piezoelectricity Applications L1 : Solid State Physics Solid state physics is the study of rigid matter, or solids, ,through methods such as quantum mechanics, crystallography, electromagnetism and metallurgy. It is the largest branch of condensed matter physics. Solid-state physics studies how the large-scale properties of solid materials result from their atomic- scale properties. Thus, solid-state physics forms the theoretical basis of materials science. It also has direct applications, for example in the technology of transistors and semiconductors. Crystalline solids & Amorphous solids Solid materials are formed from densely-packed atoms, which interact intensely. These interactions produce : the mechanical (e.g. hardness and elasticity), thermal, electrical, magnetic and optical properties of solids. Depending on the material involved and the conditions in which it was formed , the atoms may be arranged in a regular, geometric pattern (crystalline solids, which include metals and ordinary water ice) , or irregularly (an amorphous solid such as common window glass). Crystalline solids & Amorphous solids The bulk of solid-state physics theory and research is focused on crystals. -

Lecture 3: Fermi-Liquid Theory 1 General Considerations Concerning Condensed Matter
Phys 769 Selected Topics in Condensed Matter Physics Summer 2010 Lecture 3: Fermi-liquid theory Lecturer: Anthony J. Leggett TA: Bill Coish 1 General considerations concerning condensed matter (NB: Ultracold atomic gasses need separate discussion) Assume for simplicity a single atomic species. Then we have a collection of N (typically 1023) nuclei (denoted α,β,...) and (usually) ZN electrons (denoted i,j,...) interacting ∼ via a Hamiltonian Hˆ . To a first approximation, Hˆ is the nonrelativistic limit of the full Dirac Hamiltonian, namely1 ~2 ~2 1 e2 1 Hˆ = 2 2 + NR −2m ∇i − 2M ∇α 2 4πǫ r r α 0 i j Xi X Xij | − | 1 (Ze)2 1 1 Ze2 1 + . (1) 2 4πǫ0 Rα Rβ − 2 4πǫ0 ri Rα Xαβ | − | Xiα | − | For an isolated atom, the relevant energy scale is the Rydberg (R) – Z2R. In addition, there are some relativistic effects which may need to be considered. Most important is the spin-orbit interaction: µ Hˆ = B σ (v V (r )) (2) SO − c2 i · i × ∇ i Xi (µB is the Bohr magneton, vi is the velocity, and V (ri) is the electrostatic potential at 2 3 2 ri as obtained from HˆNR). In an isolated atom this term is o(α R) for H and o(Z α R) for a heavy atom (inner-shell electrons) (produces fine structure). The (electron-electron) magnetic dipole interaction is of the same order as HˆSO. The (electron-nucleus) hyperfine interaction is down relative to Hˆ by a factor µ /µ 10−3, and the nuclear dipole-dipole SO n B ∼ interaction by a factor (µ /µ )2 10−6. -

Arxiv:2007.08348V3
Dynamical transitions and critical behavior between discrete time crystal phases 1 1,2, Xiaoqin Yang and Zi Cai ∗ 1Wilczek Quantum Center and Key Laboratory of Artificial Structures and Quantum Control, School of Physics and Astronomy, Shanghai Jiao Tong University, Shanghai 200240, China 2Shanghai Research Center for Quantum Sciences, Shanghai 201315, China In equilibrium physics, spontaneous symmetry breaking and elementary excitation are two con- cepts closely related with each other: the symmetry and its spontaneous breaking not only control the dynamics and spectrum of elementary excitations, but also determine their underlying struc- tures. In this paper, based on an exactly solvable model, we propose a phase ramping protocol to study an excitation-like behavior of a non-equilibrium quantum matter: a discrete time crystal phase with spontaneous temporal translational symmetry breaking. It is shown that slow ramp- ing could induce a dynamical transition between two Z2 symmetry breaking time crystal phases in time domain, which can be considered as a temporal analogue of the soliton excitation spacially sandwiched by two degenerate charge density wave states in polyacetylene. By tuning the ramping rate, we observe a critical value at which point the transition duration diverges, resembling the critical slowing down phenomenon in nonequilibrium statistic physics. We also discuss the effect of stochastic sequences of such phase ramping processes and its implication to the stability of the discrete time crystal phase against noisy perturbations. Usually, the ground state energy of an equilibrium sys- question is how to generalize such an idea into the non- tem does not have much to do with its observable behav- equilibirum quantum matters with intriguing SSB absent ior. -

A Short Review of Phonon Physics Frijia Mortuza
International Journal of Scientific & Engineering Research Volume 11, Issue 10, October-2020 847 ISSN 2229-5518 A Short Review of Phonon Physics Frijia Mortuza Abstract— In this article the phonon physics has been summarized shortly based on different articles. As the field of phonon physics is already far ad- vanced so some salient features are shortly reviewed such as generation of phonon, uses and importance of phonon physics. Index Terms— Collective Excitation, Phonon Physics, Pseudopotential Theory, MD simulation, First principle method. —————————— —————————— 1. INTRODUCTION There is a collective excitation in periodic elastic arrangements of atoms or molecules. Melting transition crystal turns into liq- uid and it loses long range transitional order and liquid appears to be disordered from crystalline state. Collective dynamics dispersion in transition materials is mostly studied with a view to existing collective modes of motions, which include longitu- dinal and transverse modes of vibrational motions of the constituent atoms. The dispersion exhibits the existence of collective motions of atoms. This has led us to undertake the study of dynamics properties of different transitional metals. However, this collective excitation is known as phonon. In this article phonon physics is shortly reviewed. 2. GENERATION AND PROPERTIES OF PHONON Generally, over some mean positions the atoms in the crystal tries to vibrate. Even in a perfect crystal maximum amount of pho- nons are unstable. As they are unstable after some time of period they come to on the object surface and enters into a sensor. It can produce a signal and finally it leaves the target object. In other word, each atom is coupled with the neighboring atoms and makes vibration and as a result phonon can be found [1]. -

Time-Domain Grating with a Periodically Driven Qutrit
PHYSICAL REVIEW APPLIED 11, 014053 (2019) Time-Domain Grating with a Periodically Driven Qutrit Yingying Han,1,2,3,§ Xiao-Qing Luo,2,3,§ Tie-Fu Li,4,2,* Wenxian Zhang,1,† Shuai-Peng Wang,2 J.S. Tsai,5,6 Franco Nori,5,7 and J.Q. You3,2,‡ 1 School of Physics and Technology, Wuhan University, Wuhan, Hubei 430072, China 2 Quantum Physics and Quantum Information Division, Beijing Computational Science Research Center, Beijing 100193, China 3 Interdisciplinary Center of Quantum Information and Zhejiang Province Key Laboratory of Quantum Technology and Device, Department of Physics and State Key Laboratory of Modern Optical Instrumentation, Zhejiang University, Hangzhou 310027, China 4 Institute of Microelectronics, Department of Microelectronics and Nanoelectronics, and Tsinghua National Laboratory of Information Science and Technology, Tsinghua University, Beijing 100084, China 5 Theoretical Quantum Physics Laboratory, RIKEN Cluster for Pioneering Research, Wako-shi, Saitama 351-0198, Japan 6 Department of Physic, Tokyo University of Science, Kagurazaka, Shinjuku-ku, Tokyo 162-8601, Japan 7 Department of Physics, The University of Michigan, Ann Arbor, Michigan 48109-1040, USA (Received 23 October 2018; revised manuscript received 3 December 2018; published 28 January 2019) Physical systems in the time domain may exhibit analogous phenomena in real space, such as time crystals, time-domain Fresnel lenses, and modulational interference in a qubit. Here, we report the experi- mental realization of time-domain grating using a superconducting qutrit in periodically modulated probe and control fields via two schemes: simultaneous modulation and complementary modulation. Both exper- imental and numerical results exhibit modulated Autler-Townes (AT) and modulation-induced diffraction (MID) effects. -

Magnetic Manipulation of Polymeric Nanostructures
Magnetic Manipulation of Polymeric Nanostructures R.S.M. Rikken 1,2, H. Engelkamp 1, R.J.M. Nolte 2, J.C. Maan 1, J.C.M. van Hest 2, D.A. Wilson 2, P.C.M. Christianen 1* 1 High Field Magnet Laboratory (HFML-EMFL), Radboud University, Toernooiveld 7, 6525 ED Nijmegen, The Netherlands 2 Institute for Molecules and Materials, Radboud University, Heyendaalseweg 135, 6525 AJ Nijmegen, The Netherlands *corresponding author: [email protected] Polymersomes are bilayer vesicles self-assembled from amphiphilic block copolymers. They are ideal and versatile nano-objects since they have many adjustable properties such as their flexibility, permeability and functionality, which can be used as nano-containers and nanomotors for nanochemistry and drug delivery [1, 2]. We have recently developed a polymersome system using poly(ethylene glycol)-polystyrene (PEG-PS) block copolymers. PEG-PS polymersomes have the advantage that their flexibility can be controlled by the contents of organic solvents like THF and dioxane, which act as a plasticizer on the polystyrene membrane. It also allows flexible polymersomes to be fixated by adding an excess of water. For many applications, the shape of a polymersome is very important since shape and functionality are closely related. In this talk an overview will be given of our efforts to control the shape of polymersomes by application of osmotic and/or magnetic forces. It will be shown that high magnetic fields can be used in two different ways: either to probe the polymersome shape using magnetic alignment or to modify the shape by magnetic deformation. We have investigated two different methods in which an osmotic pressure is used to change the polymersome shape. -

Introduction to Solid State Physics
Introduction to Solid State Physics Sonia Haddad Laboratoire de Physique de la Matière Condensée Faculté des Sciences de Tunis, Université Tunis El Manar S. Haddad, ASP2021-23-07-2021 1 Outline Lecture I: Introduction to Solid State Physics • Brief story… • Solid state physics in daily life • Basics of Solid State Physics Lecture II: Electronic band structure and electronic transport • Electronic band structure: Tight binding approach • Applications to graphene: Dirac electrons Lecture III: Introduction to Topological materials • Introduction to topology in Physics • Quantum Hall effect • Haldane model S. Haddad, ASP2021-23-07-2021 2 It’s an online lecture, but…stay focused… there will be Quizzes and Assignments! S. Haddad, ASP2021-23-07-2021 3 References Introduction to Solid State Physics, Charles Kittel Solid State Physics Neil Ashcroft and N. Mermin Band Theory and Electronic Properties of Solids, John Singleton S. Haddad, ASP2021-23-07-2021 4 Outline Lecture I: Introduction to Solid State Physics • A Brief story… • Solid state physics in daily life • Basics of Solid State Physics Lecture II: Electronic band structure and electronic transport • Tight binding approach • Applications to graphene: Dirac electrons Lecture III: Introduction to Topological materials • Introduction to topology in Physics • Quantum Hall effect • Haldane model S. Haddad, ASP2021-23-07-2021 5 Lecture I: Introduction to solid state Physics What is solid state Physics? Condensed Matter Physics (1960) solids Soft liquids Complex Matter systems Optical lattices, Non crystal Polymers, liquid crystal Biological systems (glasses, crystals, colloids s Economic amorphs) systems Neurosystems… S. Haddad, ASP2021-23-07-2021 6 Lecture I: Introduction to solid state Physics What is condensed Matter Physics? "More is different!" P.W. -
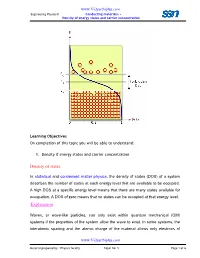
Density of States Explanation
www.Vidyarthiplus.com Engineering Physics-II Conducting materials- - Density of energy states and carrier concentration Learning Objectives On completion of this topic you will be able to understand: 1. Density if energy states and carrier concentration Density of states In statistical and condensed matter physics , the density of states (DOS) of a system describes the number of states at each energy level that are available to be occupied. A high DOS at a specific energy level means that there are many states available for occupation. A DOS of zero means that no states can be occupied at that energy level. Explanation Waves, or wave-like particles, can only exist within quantum mechanical (QM) systems if the properties of the system allow the wave to exist. In some systems, the interatomic spacing and the atomic charge of the material allows only electrons of www.Vidyarthiplus.com Material prepared by: Physics faculty Topic No: 5 Page 1 of 6 www.Vidyarthiplus.com Engineering Physics-II Conducting materials- - Density of energy states and carrier concentration certain wavelengths to exist. In other systems, the crystalline structure of the material allows waves to propagate in one direction, while suppressing wave propagation in another direction. Waves in a QM system have specific wavelengths and can propagate in specific directions, and each wave occupies a different mode, or state. Because many of these states have the same wavelength, and therefore share the same energy, there may be many states available at certain energy levels, while no states are available at other energy levels. For example, the density of states for electrons in a semiconductor is shown in red in Fig. -

Solid State Physics
1 Solid State Physics Semiclassical motion in a magnetic ¯eld 16 Lecture notes by Quantization of the cyclotron orbit: Landau levels 16 Michael Hilke Magneto-oscillations 17 McGill University (v. 10/25/2006) Phonons: lattice vibrations 17 Mono-atomic phonon dispersion in 1D 17 Optical branch 18 Experimental determination of the phonon Contents dispersion 18 Origin of the elastic constant 19 Introduction 2 Quantum case 19 The Theory of Everything 3 Transport (Boltzmann theory) 21 Relaxation time approximation 21 H2O - An example 3 Case 1: F~ = ¡eE~ 21 Di®usion model of transport (Drude) 22 Binding 3 Case 2: Thermal inequilibrium 22 Van der Waals attraction 3 Physical quantities 23 Derivation of Van der Waals 3 Repulsion 3 Semiconductors 24 Crystals 3 Band Structure 24 Ionic crystals 4 Electron and hole densities in intrinsic (undoped) Quantum mechanics as a bonder 4 semiconductors 25 Hydrogen-like bonding 4 Doped Semiconductors 26 Covalent bonding 5 Carrier Densities in Doped semiconductor 27 Metals 5 Metal-Insulator transition 27 Binding summary 5 In practice 28 p-n junction 28 Structure 6 Illustrations 6 One dimensional conductance 29 Summary 6 More than one channel, the quantum point Scattering 6 contact 29 Scattering theory of everything 7 1D scattering pattern 7 Quantum Hall e®ect 30 Point-like scatterers on a Bravais lattice in 3D 7 General case of a Bravais lattice with basis 8 superconductivity 30 Example: the structure factor of a BCC lattice 8 BCS theory 31 Bragg's law 9 Summary of scattering 9 Properties of Solids and liquids 10 single electron approximation 10 Properties of the free electron model 10 Periodic potentials 11 Kronig-Penney model 11 Tight binging approximation 12 Combining Bloch's theorem with the tight binding approximation 13 Weak potential approximation 14 Localization 14 Electronic properties due to periodic potential 15 Density of states 15 Average velocity 15 Response to an external ¯eld and existence of holes and electrons 15 Bloch oscillations 16 2 INTRODUCTION derived based on a periodic lattice.