Minimal Euclidean Representations of Graphs
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

TETRAVALENT SYMMETRIC GRAPHS of ORDER 9P
J. Korean Math. Soc. 49 (2012), No. 6, pp. 1111–1121 http://dx.doi.org/10.4134/JKMS.2012.49.6.1111 TETRAVALENT SYMMETRIC GRAPHS OF ORDER 9p Song-Tao Guo and Yan-Quan Feng Abstract. A graph is symmetric if its automorphism group acts transi- tively on the set of arcs of the graph. In this paper, we classify tetravalent symmetric graphs of order 9p for each prime p. 1. Introduction Let G be a permutation group on a set Ω and α ∈ Ω. Denote by Gα the stabilizer of α in G, that is, the subgroup of G fixing the point α. We say that G is semiregular on Ω if Gα = 1 for every α ∈ Ω and regular if G is transitive and semiregular. Throughout this paper, we consider undirected finite connected graphs without loops or multiple edges. For a graph X we use V (X), E(X) and Aut(X) to denote its vertex set, edge set, and automorphism group, respectively. For u , v ∈ V (X), denote by {u , v} the edge incident to u and v in X. A graph X is said to be vertex-transitive if Aut(X) acts transitively on V (X). An s-arc in a graph is an ordered (s + 1)-tuple (v0, v1,...,vs−1, vs) of vertices of the graph X such that vi−1 is adjacent to vi for 1 ≤ i ≤ s, and vi−1 = vi+1 for 1 ≤ i ≤ s − 1. In particular, a 1-arc is called an arc for short and a 0-arc is a vertex. -

Cores of Vertex-Transitive Graphs
Cores of Vertex-Transitive Graphs Ricky Rotheram Submitted in total fulfilment of the requirements of the degree of Master of Philosophy October 2013 Department of Mathematics and Statistics The University of Melbourne Parkville, VIC 3010, Australia Produced on archival quality paper Abstract The core of a graph Γ is the smallest graph Γ∗ for which there exist graph homomor- phisms Γ ! Γ∗ and Γ∗ ! Γ. Thus cores are fundamental to our understanding of general graph homomorphisms. It is known that for a vertex-transitive graph Γ, Γ∗ is vertex-transitive, and that jV (Γ∗)j divides jV (Γ)j. The purpose of this thesis is to determine the cores of various families of vertex-transitive and symmetric graphs. We focus primarily on finding the cores of imprimitive symmetric graphs of order pq, where p < q are primes. We choose to investigate these graphs because their cores must be symmetric graphs with jV (Γ∗)j = p or q. These graphs have been completely classified, and are split into three broad families, namely the circulants, the incidence graphs and the Maruˇsiˇc-Scapellato graphs. We use this classification to determine the cores of all imprimitive symmetric graphs of order pq, using differ- ent approaches for the circulants, the incidence graphs and the Maruˇsiˇc-Scapellato graphs. Circulant graphs are examples of Cayley graphs of abelian groups. Thus, we generalise the approach used to determine the cores of the symmetric circulants of order pq, and apply it to other Cayley graphs of abelian groups. Doing this, we show that if Γ is a Cayley graph of an abelian group, then Aut(Γ∗) contains a transitive subgroup generated by semiregular automorphisms, and either Γ∗ is an odd cycle or girth(Γ∗) ≤ 4. -

Trivalent Orbit Polynomial Graphs* Robert A. Beezer Department Of
CORE Metadata, citation and similar papers at core.ac.uk Provided by Elsevier - Publisher Connector Trivalent Orbit Polynomial Graphs* Robert A. Beezer Department of Mathematics & Computer Science University of Puget Sound Tacoma, Washington 98416 Submittedby Richard A. Brualdi ABSTRACT We introduce orbit polynomial graphs, and discuss their connections with dis- tance-transitive, distance-regular, and distance polynomial graphs. After some general results, we classify all of the nonsymmetric trivalent orbit polynomial graphs. 1. INTRODUCTION Given a finite, undirected graph I with no loops or multiple edges, there are many connections between its automorphism group, adjacency algebra, eigenvalues, and distance structure. We will introduce the notion of an orbit polynomial graph, and discuss its relationship to distance-transitive, distance- regular, and distance polynomial graphs. Then we will find all of the nonsymmetric trivalent orbit polynomial graphs. For a graph I, the adjacency matrix A( I) = (a i j) is given by 1 if {vi,vj}EEI, aij = 0 otherwise. The adjacency algebra of I, st( I), is the algebra of all polynomials in A( I). The eigenvalues of I are the eigenvalues of A(I), and the number of distinct eigenvalues of I will be denoted here as e(I). Because A(T) is a real symmetric matrix, e(I) equals the dimension of Q(r). *This work was supportedin part by the Research Board of the University of Illinois at Urbana-Champaign. LINEAR ALGEBRA AND ITS APPLZCATZONS 73:133-146 (1986) 133 0 Elsevier Science Publishing Co., Inc., 1986 52 Vanderbilt Ave., New York, NY 10017 00243795/86/$3.50 134 ROBERT A. -

An Introduction to Algebraic Graph Theory
An Introduction to Algebraic Graph Theory Cesar O. Aguilar Department of Mathematics State University of New York at Geneseo Last Update: March 25, 2021 Contents 1 Graphs 1 1.1 What is a graph? ......................... 1 1.1.1 Exercises .......................... 3 1.2 The rudiments of graph theory .................. 4 1.2.1 Exercises .......................... 10 1.3 Permutations ........................... 13 1.3.1 Exercises .......................... 19 1.4 Graph isomorphisms ....................... 21 1.4.1 Exercises .......................... 30 1.5 Special graphs and graph operations .............. 32 1.5.1 Exercises .......................... 37 1.6 Trees ................................ 41 1.6.1 Exercises .......................... 45 2 The Adjacency Matrix 47 2.1 The Adjacency Matrix ...................... 48 2.1.1 Exercises .......................... 53 2.2 The coefficients and roots of a polynomial ........... 55 2.2.1 Exercises .......................... 62 2.3 The characteristic polynomial and spectrum of a graph .... 63 2.3.1 Exercises .......................... 70 2.4 Cospectral graphs ......................... 73 2.4.1 Exercises .......................... 84 3 2.5 Bipartite Graphs ......................... 84 3 Graph Colorings 89 3.1 The basics ............................. 89 3.2 Bounds on the chromatic number ................ 91 3.3 The Chromatic Polynomial .................... 98 3.3.1 Exercises ..........................108 4 Laplacian Matrices 111 4.1 The Laplacian and Signless Laplacian Matrices .........111 4.1.1 -

On a Class of Finite Symmetric Graphs
ARTICLE IN PRESS European Journal of Combinatorics ( ) – www.elsevier.com/locate/ejc On a class of finite symmetric graphs Sanming Zhou1 Department of Mathematics and Statistics, The University of Melbourne, Parkville, VIC 3010, Australia Received 15 March 2006; accepted 2 April 2007 Dedicated to Professor Yixun Lin with best wishes on the occasion of his 70th birthday Abstract Let Γ be a G-symmetric graph, and let B be a nontrivial G-invariant partition of the vertex set of Γ . This paper aims to characterize (Γ , G) under the conditions that the quotient graph ΓB is (G, 2)-arc transitive and the induced subgraph between two adjacent blocks is 2 · K2 or K2,2. The results answer two questions about the relationship between Γ and ΓB for this class of graphs. c 2007 Elsevier Ltd. All rights reserved. 1. Introduction The purpose of this paper is to answer two questions [8] regarding 2-arc transitivity of quotient graphs for a class of finite symmetric graphs. Let Γ = (V (Γ ), E(Γ )) be a finite graph. For an integer s ≥ 1, an s-arc of Γ is an (s+1)-tuple (α0, α1, . , αs) of vertices of Γ such that αi , αi+1 are adjacent for i = 0,..., s − 1 and αi−1 6= αi+1 for i = 1,..., s −1. We will use Arcs(Γ ) to denote the set of s-arcs of Γ , and Arc(Γ ) in place of Arc1(Γ ). Γ is said to admit a group G as a group of automorphisms if G acts on V (Γ ) and preserves the adjacency of Γ , that is, for any α, β ∈ V (Γ ) and g ∈ G, α and β are adjacent in Γ if and only if αg and βg are adjacent in Γ . -

Symmetric Graph Properties Have Independent Edges
Symmetric Graph Properties Have Independent Edges Dimitris Achlioptasa,b,1,2, Paris Siminelakisc,1,3,∗ aDepartment of Computer Science University of California, Santa Cruz bDepartment of Informatics & Telecommunications, University of Athens cDepartment of Electrical Engineering, Stanford University Abstract In the study of random structures we often face a trade-off between realism and tractability, the latter typically enabled by independence assumptions. In this work we initiate an effort to bridge this gap by developing tools that allow us to work with independence without assuming it. Let Gn be the set of all graphs on n vertices and let S be an arbitrary subset of Gn, e.g., the set of all graphs with m edges. The study of random networks can be seen as the study of properties that are true for most elements of S, i.e., that are true with high probability for a uniformly random element of S. With this in mind, we pursue the following question: What are general sufficient conditions for the uniform measure on a set of graphs S ⊆ Gn to be well- approximable by a product measure on the set of all possible edges? Keywords: Random Graphs, Symmetric Graph Properties Concentration of Measure, Approximate Independence ∗Corresponding author Email addresses: [email protected] (Dimitris Achlioptas), [email protected] (Paris Siminelakis) 1Research supported by ERC Starting Grant StG-210743. 2Research supported by NSF Grant CCF-1514128, an Alfred P. Sloan Fellowship, the European Union (European Social Fund ESF) and Greek national funds through the Op- erational Program \Education and Lifelong Learning" of the National Strategic Reference Framework (NSRF) - Research Funding Program: ARISTEIA II. -

A Class of Vertex-Transitive Digraphs the Graphs We Consider
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector JOURNAL OF COMBINATORIAL THEORY (B), 14, 246-255 (1973) A Class of Vertex-Transitive Digraphs CHONG-YUN CHAO University of Pittsburgh, Pittsburgh, Pennsylvania 15213 AND JACQUELINEG. WELLS Pennsylvania State University, McKeesport, Pennsylvania 15132 Communicated by W. T. Tutte ReceivedJune 6, 1972 1. We determineall the symmetricdigraphs with a prime number,p, of vertices.We alsodetermine the structureof their groups.Our resultsare similar to the caseof undirectedgraphs. But someof the proofsare simpler. 2. The isomorphicclasses of the vertex-transitivedigraphs with p vertices are enumerated. 3. We statean algorithmfor obtainingthe group of any givenvertex-transi- tive digraphwith p vertices.The algorithmgives a partial answerfor the open problem2 on page301 in [7]. 1. INTRODUCTION The graphs we consider here are finite and simple digraphs (directed graphs) without loops. A digraph X is said to be vertex-transitive if its group of automorphisms, G(X), is transitive on its vertices V(X). X is said to be edge-transitive if G(X) is transitive on its edges E(X). X is said to be a symmetric graph if it is both vertex-transitive and edge-transitive. In [3], one of us classified all symmetric undirected graphs with a prime number, p, of vertices. Since undirected graphs may be considered as a special case of digraphs, here we generalize the results in [3] to digraphs, and present an algorithm for obtaining the group of automorphisms of a given vertex- transitive digraph with p vertices, i.e., in Section 2, we show that, besides non-complete and non-null digraphs with p vertices, there exists a sym- metric digraph withp vertices and degree m, 1 < m < p - 1, if and only if m divides p - 1. -

Distance-Transitive Graphs
Distance-Transitive Graphs Submitted for the module MATH4081 Robert F. Bailey (4MH) Supervisor: Prof. H.D. Macpherson May 10, 2002 2 Robert Bailey Department of Pure Mathematics University of Leeds Leeds, LS2 9JT May 10, 2002 The cover illustration is a diagram of the Biggs-Smith graph, a distance-transitive graph described in section 11.2. Foreword A graph is distance-transitive if, for any two arbitrarily-chosen pairs of vertices at the same distance, there is some automorphism of the graph taking the first pair onto the second. This project studies some of the properties of these graphs, beginning with some relatively simple combinatorial properties (chapter 2), and moving on to dis- cuss more advanced ones, such as the adjacency algebra (chapter 7), and Smith’s Theorem on primitive and imprimitive graphs (chapter 8). We describe four infinite families of distance-transitive graphs, these being the Johnson graphs, odd graphs (chapter 3), Hamming graphs (chapter 5) and Grass- mann graphs (chapter 6). Some group theory used in describing the last two of these families is developed in chapter 4. There is a chapter (chapter 9) on methods for constructing a new graph from an existing one; this concentrates mainly on line graphs and their properties. Finally (chapter 10), we demonstrate some of the ideas used in proving that for a given integer k > 2, there are only finitely many distance-transitive graphs of valency k, concentrating in particular on the cases k = 3 and k = 4. We also (chapter 11) present complete classifications of all distance-transitive graphs with these specific valencies. -

Symmetry and Chirality in Discrete Structures
Symmetry and chirality in discrete structures Marston Conder University of Auckland, New Zealamd UW Math Day, Seattle, March 2013 Where is New Zealand? What is New Zealand famous for? • Great place to live (South Pacific) • Multi-cultural (European, Maori/Polynesian, Asian ...) • Beautiful scenery (beaches, volcanoes, lakes, mountains) • Kiwis (strange little birds), kiwi fruit (strange little fruit) • Dairy produce (milk, butter, cheese, etc.) • Film sites (Lord of the Rings, The Hobbit, Narnia, etc.) • Rugby football • Extreme sports (bungy-jumping, white-water rafting, etc.) What is symmetry? Symmetry can mean many different things, such as balance, uniform proportion, harmony, or congruence Generally, an object has symmetry if it can be transformed in way that leaves it looking the same as it did originally. Symmetry can be reflective: ... or rotational: ... or translational: ... or a combination of these types Examples of these kinds of symmetry abound in nature ... but have also been manufactured by human fascination and enterprise e.g. the Platonic solids (c. 360BC) or earlier ... the `Neolithic Scots' (c. 2000BC) ... as publicised by Atiyah and Sutcliffe (2003) ... but unfortunately a hoax! The claim that the Scots knew about these five regular solids over 1000 years before Plato was based on the above five `Scottish stones' at the Ashmolean Museum in Oxford | but one has 14 faces, and none of them is an icosahedron [See John Baez's website for the full story] Tilings at the Alhambra Palace { on its walls, floors, ceilings, and even some of the furniture { amazingly exhibit all of the 17 \wallpaper symmetries" (in two dimensions) [Rafael P´erezG´omezand Jos´eMara Montesinos, 1980s] Symmetry can induce strength and stability: .. -

Classifying Semisymmetric Cubic Graphs of Order 20P
Turk J Math () : { ⃝c TUB¨ ITAK_ doi:10.3906/mat- 1 Classifying semisymmetric cubic graphs of order 20p 1 2∗ 2 Mohsen SHAHSAVARAN , Mohammad Reza DARAFSHEH (1) School of Mathematics, Statistics, and Computer Science, College of Science, University of Tehran, Tehran, Iran, ORCID iD: https://orcid.org/0000-0002-1416-1388 (2) School of Mathematics, Statistics, and Computer Science, College of Science, University of Tehran, Tehran, Iran, ORCID iD: https://orcid.org/0000-0002-5539-4989 Received: .201 • Accepted/Published Online: .201 • Final Version: ..201 3 4 Abstract: A simple graph is called semisymmetric if it is regular and edge transitive but not vertex transitive. In this 5 paper we classify all connected cubic semisymmetric graphs of order 20p, p prime. 6 Key words: Edge-transitive graph, vertex-transitive graph, semisymmetric graph, order of a graph, classification of 7 cubic semisymmetric graphs 8 1. Introduction 9 In this paper all graphs are finite, undirected and simple, i.e. without loops and multiple edges. A graph is 10 called semisymmetric if it is regular and edge-transitive but not vertex-transitive. 11 The class of semisymmetric graphs was first studied by Folkman [9], who found several infinite families 12 of such graphs and posed eight open problems. 13 An interesting research problem is to classify connected cubic semisymmetric graphs of various types of 2 14 orders. In [9], Folkman proved that there are no semisymmetric graphs of order 2p or 2p for any prime p. 15 The classification of semisymmetric graphs of order 2pq , where p and q are distinct primes, was given in [7]. -

A More Detailed Classification of Symmetric Cubic Graphs 1 Introduction
A more detailed classification of symmetric cubic graphs Marston Conder1 Roman Nedela2 Department of Mathematics Mathematical Institute University of Auckland Slovak Academy of Sciences Private Bag 92019 Auckland 975 49 Bansk´aBystrica New Zealand Slovakia Email: [email protected] Email: [email protected] Abstract A graph Γ is symmetric if its automorphism group acts transitively on the arcs of Γ, and s-regular if its automorphism group acts regularly on the set of s-arcs of Γ. Tutte (1947, 1959) showed that every cubic finite symmetric cubic graph is s-regular for some s ≤ 5. Djokoviˇcand Miller (1980) proved that there are seven types of arc-transitive group action on finite cubic graphs, characterised by the stabilisers of a vertex and an edge. A given finite symmetric cubic graph, however, may admit more than one type of arc-transitive group action. In this paper we determine exactly which combinations of types are possible. Some combinations are easily eliminated by existing theory, and others can be eliminated by elementary extensions of that theory. The remaining combinations give 17 classes of finite symmetric cubic graph, and for each of these, we prove the class is infinite, and determine at least one representative. For at least 14 of these 17 classes the representative we give has the minimum possible number of vertices (and we show that in two of these 14 cases every graph in the class is a cover of the smallest representative), while for the other three classes, we give the smallest examples known to us. In an Appendix, we give a table showing the class of every symmetric cubic graph on up to 768 vertices. -
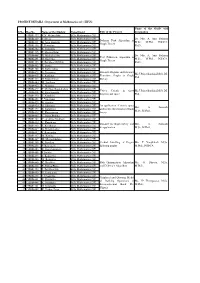
PROJECT DETAILS - Department of Mathematics (Sf) - III UG
PROJECT DETAILS - Department of Mathematics (sf) - III UG Name of the Guide with S.No Reg.No Name of the Student Department Title of the Project designation 1 15BM4423 K.N. Abiyurekha B.Sc Mathematics (SF) 2 15BM4429 S. Divya B.Sc Mathematics (SF) Dr. Mrs. A. Anis Fathima, Bellman Ford Algorithm in 3 15BM4431 K. Jaya Alamelu B.Sc Mathematics (SF) M.Sc., M.Phil., PGDCA., Graph Theory 4 15BM4456 J. Powmiya B.Sc Mathematics (SF) Ph.D., 5 15BM4464 R. Sumithra B.Sc Mathematics (SF) 6 15BM4445 P. Manimekalai B.Sc Mathematics (SF) 7 15BM4446 B. Muthukavitha B.Sc Mathematics (SF) Dr. Mrs. A. Anis Fathima, Ford Fulkerson Algorithm in 8 15BM4451 G. Naveena B.Sc Mathematics (SF) M.Sc., M.Phil., PGDCA., Graph Theory 9 15BM4453 S. Pavithra(15/7/98) B.Sc Mathematics (SF) Ph.D., 10 15BM4462 R. Sneha B.Sc Mathematics (SF) 11 15BM4426 D. Baby sudha B.Sc Mathematics (SF) 12 15BM4428 A. Devipriya B.Sc Mathematics (SF) Distance Regular and Distance Ms.J.Priyadharshini,M.Sc.,M. 13 15BM4435 S. Karthika B.Sc Mathematics (SF) Transitive Graphs in Graph Phil., 14 15BM4444 G. Maheshwari B.Sc Mathematics (SF) Theory 15 15BM4460 M. Santhiya B.Sc Mathematics (SF) 16 15BM4422 S. Abinaya B.Sc Mathematics (SF) 17 15BM4427 T. Chellam Rajalakshmi B.Sc Mathematics (SF) Vector Calculs in three Ms.J.Priyadharshini,M.Sc.,M. 18 15BM4436 K. Kavibharathi B.Sc Mathematics (SF) dimensional space Phil., 19 15BM4450 S. Nandhini B.Sc Mathematics (SF) 20 15BM4468 J. Vinothini B.Sc Mathematics (SF) 21 15BM4425 B.