A Derivation of =
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Caltech News
Volume 16, No.7, December 1982 CALTECH NEWS pounds, became optional and were Three Caltech offered in the winter and spring. graduate programs But under this plan, there was an overlap in material that diluted the rank number one program's efficiency, blending per in nationwide survey sons in the same classrooms whose backgrounds varied widely. Some Caltech ranked number one - students took 3B and 3C before either alone or with other institutions proceeding on to 46A and 46B, - in a recent report that judged the which focused on organic systems, scholastic quality of graduate pro" while other students went directly grams in mathematics and science at into the organic program. the nation's major research Another matter to be addressed universities. stemmed from the fact that, across Caltech led the field in geoscience, the country, the lines between inor and shared top rankings with Har ganic and organic chemistry had ' vard in physics. The Institute was in become increasingly blurred. Explains a four-way tie for first in chemistry Professor of Chemistry Peter Der with Berkeley, Harvard, and MIT. van, "We use common analytical The report was the result of a equipment. We are both molecule two-year, $500,000 study published builders in our efforts to invent new under the sponsorship of four aca materials. We use common bonds for demic groups - the American Coun The Mead Laboratory is the setting for Chemistry 5, where Carlotta Paulsen uses a rotary probing how chemical bonds are evaporator to remove a solvent from a synthesized product. Paulsen is a junior majoring in made and broken." cil of Learned Societies, the American chemistry. -

A Maxwell's Equations Primer
A Dash of Maxwell’s A Maxwell’s Equations Primer Chapter I – An Introduction By Glen Dash, Ampyx LLC, GlenDash at alum.mit.edu Copyright 2000, 2005 Ampyx LLC And God said, Let there be light: and there was light. --Genesis 1:3 And God said, Let: ∇ ⋅ D = ρ ∇ ⋅ B = 0 ∂D ∇× H = J + ∂t ∂B ∇× E = − ∂t and there was light. --Anonymous Maxwell’s Equations are eloquently simple yet excruciatingly complex. Their first statement by James Clerk Maxwell in 1864 heralded the beginning of the age of radio and, one could argue, the age of modern electronics as well. Maxwell pulled back the curtain on one of the fundamental secrets of the universe. These equations just don’t give the scientist or engineer insight, they are literally the answer to everything RF. The problem is that the equations can be baffling to work with. Solving Maxwell’s Equations for even simple structures like dipole antennas is not a trivial task. In fact, it will take us several chapters to get there. Solving Maxwell’s Equations for real life situations, like predicting the RF emissions from a cell tower, requires more mathematical horsepower than any individual mind can muster. For problems like that we turn to computers for solutions. Computational solutions to Maxwell’s Equations is a field that offers great promise. Unfortunately, that does not necessarily mean great answers. Computational solutions to Maxwell’s Equations need to be subjected to a reality check. That, in turn, usually requires a real live scientist or engineer who understands Maxwell’s Equations. -
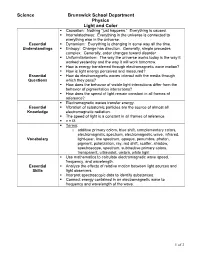
Essential Understandings
Science Brunswick School Department Physics Light and Color . Causation: Nothing “just happens.” Everything is caused. Interrelatedness: Everything in the universe is connected to everything else in the universe. Essential . Dynamism: Everything is changing in some way all the time. Understandings . Entropy: Change has direction. Generally, simple precedes complex. Generally, order changes toward disorder. Uniformitarianism: The way the universe works today is the way it worked yesterday and the way it will work tomorrow. How is energy transferred through electromagnetic wave motion? . How is light energy perceived and measured? Essential . How do electromagnetic waves interact with the media through Questions which they pass? . How does the behavior of visible light interactions differ from the behavior of pigmentation interactions? . How does the speed of light remain constant in all frames of reference? . Electromagnetic waves transfer energy. Essential . Vibration of subatomic particles are the source of almost all Knowledge electromagnetic radiation. The speed of light is a constant in all frames of reference. v = fλ . Terms: o additive primary colors, blue shift, complementary colors, electromagnetic spectrum, electromagnetic wave, infrared, Vocabulary light-year, line spectrum, opaque, penumbra, photon, pigment, polarization, ray, red shift, scatter, shadow, spectroscope, spectrum, subtractive primary colors, transparent, ultraviolet, umbra, white light . Use mathematics to calculate electromagnetic wave speed, frequency, and wavelength. Essential . Analyze the effects of relative motion between light sources and Skills light observers. Interpret spectroscopic data to identify substances. Connect energy contained in an electromagnetic wave to frequency and wavelength of the wave. 1 of 3 Science Brunswick School Department Physics Light and Color Science and Technology D. -

Maxwell=S Primer
A Dash of Maxwell’s A Maxwell’s Equations Primer Chapter III – The Difference a Del Makes By Glen Dash, Ampyx LLC, GlenDash at alum.mit.edu Copyright 2000, 2005 Ampyx LLC In Chapter Two, I introduced Maxwell’s Equations in their “integral form.” Simple in concept, the integral form can be devilishly difficult to work with. To overcome that, scientists and engineers have evolved a number of different ways to look at the problem, including this, the “differential form of the Equations.” The differential form makes use of vector operations. A physical phenomena that has the both the attributes of magnitude and direction may be described by a vector. Velocity can be drawn in vector form; it has the attributes of both direction and speed. Vectors can be illustrated graphically as shown in Figure 1(a) – the length of the vector represents its magnitude and its angle from the x axis defines its direction. However, we will be using Cartesian coordinates. In this system, vectors are described as a sum of “unit” denominated vectors. A unit vector along the x axis is simply a vector aligned with the x axis that is one unit long (one meter long in the MKS system). We’ll denote a unit vector in the x direction as i. Similarly, unit vectors in the y and z directions will be denoted j and k respectively. The vector shown in Figure 1 has a magnitude of 5 and is angled away from the x axis by 30 degrees. It can also be described as the sum of two unit denominated vectors one 3j units long and the other 4i units long. -

Download/Qbell80.Pdf (Accessed on 12 January 2021)
entropy Article Beyond Causal Explanation: Einstein’s Principle Not Reichenbach’s Michael Silberstein 1,2,* , William Mark Stuckey 3 and Timothy McDevitt 4 1 Department of Philosophy, Elizabethtown College, Elizabethtown, PA 17022, USA 2 Department of Philosophy, University of Maryland, College Park, MD 20742, USA 3 Department of Physics, Elizabethtown College, Elizabethtown, PA 17022, USA; [email protected] 4 Department of Mathematical Sciences, Elizabethtown College, Elizabethtown, PA 17022, USA; [email protected] * Correspondence: [email protected] Abstract: Our account provides a local, realist and fully non-causal principle explanation for EPR correlations, contextuality, no-signalling, and the Tsirelson bound. Indeed, the account herein is fully consistent with the causal structure of Minkowski spacetime. We argue that retrocausal accounts of quantum mechanics are problematic precisely because they do not fully transcend the assumption that causal or constructive explanation must always be fundamental. Unlike retrocausal accounts, our principle explanation is a complete rejection of Reichenbach’s Principle. Furthermore, we will argue that the basis for our principle account of quantum mechanics is the physical principle sought by quantum information theorists for their reconstructions of quantum mechanics. Finally, we explain why our account is both fully realist and psi-epistemic. Keywords: EPR correlations; relativity principle; principle explanation; Reichenbach’s Princi- ple; retrocausality; locality; contextuality; no preferred reference frame; causal modelling; no- signalling; quantum information theory; reconstructions of quantum mechanics; Tsirelson bound; realist psi-epistemic Citation: Silberstein, M.; Stuckey, W.M.; McDevitt, T. Beyond Causal 1. Introduction Explanation: Einstein’s Principle Not There is a class of interpretations or accounts of quantum mechanics (QM) called Entropy 2021 23 Reichenbach’s. -

And Others Physics 20-30 Background, Exemplars And
DOCUMENT RESUME ED 404 140 SE 054 982 AUTHOR Hackman, Desiree; And Others TITLE Physics 20-30 Background, Exemplars and Resources. INSTITUTION Alberta Dept. of Education, Edmonton. Curriculum Branch. REPORT NO ISBN-0-7732-1179-9 PUB DATE 94 NOTE 141p. AVAILABLE FROM Learning Resources Distributing Centre, 12360-142 Street, Edmonton, Alberta T5L 4X9, Canada. PUB TYPE Reports Research/Technical (143) EDRS PRICE MF01/PC06 Plus Postage. DESCRIPTORS *Biology; *Educational Resources; Foreign Countries; Light; Motion; *Physics; *Science Curriculum; *Science Education; *Science Instruction; Science Programs; *Secondary Education IDENTIFIERS Alberta; *Biology 2030 ABSTRACT This document is designed to provide practical information for teaching the Physics 20-30 Program of Studies. The first section provides an overview of Physics 20, explaining the program philosophy and the selection and sequencing of topics. The use of concept connections and teaching a course around thescience themes are described, as well as how the program articulates with the junior and senior high science courses. Section two contains four units. Unit one, "Kinematics and Dynamics", looks at the relationship among acceleration, displacement, velocity, and time. Unit two, "Circular Motion and Gravitation", emphasizes change, energy, and systems. Unit three, "Mechanical Waves" focuses on resonance. Unit four, "Light", emphasizes diversity and energy. For Physics 30, unit four (one unit) presents "Nature of Matter." The final section provides detailed information on a great -
DOCUMENT RESUME ED 359 028 SE 053 278 TITLE Physics AB
DOCUMENT RESUME ED 359 028 SE 053 278 TITLE Physics AB Course of Study. Publication No. SC-953. INSTITUTION Los Angeles Unified School District, CA. Office of Secondary Instruction. PUB DATE 90 NOTE 163p.; For course outlines in Biology AB and Chemistry AB, see SE 053 279-280. PUB TYPE Guides Classroom Use - Teaching Guides (For Teacher) (052) EDRS PRICE MF01/PC07 Plus Postage. DESCRIPTORS Computation; *Course Descriptions; Electricity; Heat; High Schools; Light; Mechanics (Physics); Nuclear Physics; Optics; *Physics; Relativity; *Science Activities; *Science Curriculum; Science Education; *Science Experiments; *Science Instruction; Scientific Concepts; Secondary School Science; Teaching Methods; Thermodynamics; Thinking Skills; Units of Study IDENTIFIERS California; *California Science Framework; Science Process Skills ABSTRACT This course of study is aligned with the California State Science Framework and provides students with the physics content needed to become scientifically and technologically literate and prepared for post-secondary science education. Framework themes incorporated into the course of study include patterns of change, evolution, energy, stability, systems and interaction, andscale and structure. The course of study is divided into four sections. The first section provides an overview of thecourse and includes a course description, representative objectives, a time line, and the sequence of instructional units. The second section presents the course's five instructional units and enumerates the required concepts and skills to be taught. The first uniton mechanics is covered in the first semester. The four units for the secondsemester include heat and thermodynamics; electricity, magnetism, and electromagnetism; I.ight and optics; and modern physics. The third section on lesson planning discusses various teaching strategiesthat foster scientific ways of thinking and encourage student creativity - and curiosity. -

8Th Grade - Grading Period 4 Overview
Name_________________________________________________________________________ 8th Grade - Grading Period 4 Overview Ohio's New Learning Standards Forces between objects act when the objects are in direct contact or when they are not touching. (8.PS.1) There are different types of potential energy. (8.PS.3) d Clear Learning Targets "I can" ______ identify forces that act at a distance, such as gravity, magnetism, and electrical. ______ describe some of the properties of magnets and some of the basic behaviors of magnetic forces ______ use a field model to explain the effects of forces that act at a distance. ______ generate an electric current by passing a conductive wire through a magnetic field and quantify electric current, using a galvanometer or multimeter. ______ demonstrate that the Earth has a magnetic field. ______ explain that objects and particles have stored energy due to their position from a reference point and this energy has the potential to cause motion. ______ explain that a field originates at a source and radiates away from that source decreasing in strength. ______ demonstrate how electrons transfer electrical and magnetic (electromagnetic) energy through waves. ______ plan, design, construct and implement an electromagnetic system to solve a real-world problem. Name_________________________________________________________________________ 8th Grade - Grading Period 4 Overview Essential Vocabulary/Concepts 8.PS.3 8.PS.1 Atoms Attraction Chemical Potential Energy Conductor Compression Earth’s Magnetic Field Elastic Potential -

Frequently Asked Questions About the Transfer Examinations
Undergraduate Admissions and Financial Aid Frequently Asked Questions about the Transfer Examinations What topics are covered on the Transfer Examinations? Physics: Newtonian mechanics (motion, vectors, trajectories, Newton's laws, forces), work and energy, energy conservation, momentum, rigid rotations, angular momentum, harmonic motion, resonance, gravity, Kepler orbits, ellipses, electric fields and potentials, Gauss's Law, current resistance, capacitance, inductance, magnetic fields, Faraday's law, AC and DC circuits, and special relativity. Math: Basic calculus, Taylor polynomials, series, linear algebra (systems of equations, vectors and matrices, determinants, vector spaces, transformations, eigenvalues), vector calculus (multiple integrals, line and path integrals, theorems of Green and Stokes), and differential equations. *Not all of these topics will be on your transfer exams. Please use them as a reference to study. Sample Math & Physics Textbooks: Ma 001A. Calculus of One and Several Variables and Linear Algebra. Required textbooks: • Apostol, Tom; Calculus, Vol. 1. ISBN: 0471000051 Ma 001B (Analytical). Calculus of One and Several Variables and Linear Algebra. Required textbooks: • Apostol, Tom; Calculus, Vol. 2. ISBN: 0471000078 Ma 001b (Practical). Calculus of One and Several Variables and Linear Algebra. • https://www.math.brown.edu/~treil/papers/LADW/book.pdf Ma 001C (Analytical). Calculus of One and Several Variables and Linear Algebra. Required textbooks: • Apostol, Tom; Calculus, Vol. 2. ISBN: 0471000078 Ma 001C (Practical). Calculus of One and Several Variables and Linear Algebra. Required textbooks: • Marsden, Jerrold, Tromba, Anthony; Vector Calculus (Sixth), W. H. Freeman, 2012. ISBN: 1429215089 Ma 002A (Analytical). Differential Equations, Probability, and Statistics. Required textbooks: • Robinson, James; An Introduction to Ordinary Differential Equations. ISBN: 0521533910 Ma 002A (Practical). -

Recitation 9
Recitation 9 P H Y S 2 4 1 OCTOBER 17, 2013 Clicker Question 1 Two wires carrying current i experience a no net force due to an external magnetic field. What can you say about the current in the two-wire system? A) Currents are parallel B i dl B) Currents are anti-parallel z C) Impossible to determine y x FB idl B A current i runs through a rectangular loop of wire. The wire is exposed to a uniform magnetic field. Find the net force on the wire. B F i w B z z back idl y y d Fright Fleft 0 x x F i w B w front Outline Biot-Savart Maxwell’s equations Law of Biot-Savart FB idl B idl rˆ B 0 4 r 2 T m2 4 107 0 A Group Clicker Question A wire carries current into the page. What direction is the magnetic field around the wire? A) Clockwise idl B) Counter-clockwise C) Radially outward D) Radially inward E) None of the above Group Clicker Question A wire carries current into the page. What direction is the magnetic field around the wire? idl rˆ B Group Clicker Question A wire carries current into the page. What direction is the magnetic field around the wire? idl rˆ B Group Clicker Question A wire carries current into the page. What direction is the magnetic field around the wire? idl rˆ B Right Hand Rule Shortcut for determining the Magnetic field: 1. Grab the current with your thumb pointing the direction of the flow 2. -

Chapter 32 - Magnetism of Matter; Maxwell’S Equations Problem Set #11 - Due: Ch 32 - 3, 7, 11, 18, 20, 21, 22, 30, 31, 34, 38, 45 Lecture Outline 1
Physics 4B Lecture Notes Chapter 32 - Magnetism of Matter; Maxwell’s Equations Problem Set #11 - due: Ch 32 - 3, 7, 11, 18, 20, 21, 22, 30, 31, 34, 38, 45 Lecture Outline 1. Magnets as Dipoles 2. Gauss’ Law for Magnetism 3. Magnetism in Matter 4. Three Types of Magnetic Behavior 5. Induced Magnetic Fields 6. Maxwell's Equations At this point we know the laws that describe electric fields. They are, r r q Gauss's Law for Electricity òE · dA = [Charge creates diverging E fields] eo r dF Faraday's Law of Induction E · dsr = - B [Changing B's create circulating E's] ò dt The laws that explain the properties of magnetic fields aren’t complete. As far as we know, the only way to create a magnetic field is with a current and this relationship is given by, r dq Ampere's Law B · dsr = m [Currents make circulating B fields] ò o dt In this chapter we will complete the laws of magnetism by examining magnets and by finding a way to induce magnetic fields. The complete laws of electricity and magnetism are known as “Maxwell’s Equations.” 1. Magnets as Dipoles By looking at the laws for electric fields you begin to r r wonder about òB · dA = ? . In other words, are there ways to make diverging magnetic fields. Is there something analogous to electric coil charges that produce diverging magnetic fields. The obvious guess would be a magnet. The magnetic field lines due to a coil. Magnetic Filing Demo w/ wire, coil, magnet and power supply The magnetic field of a magnet isn’t diverging. -

André-Marie Ampère, "The Newton of Electricity" André-Marie Ampère, “The Newton of Electricity”
FollowFollow us soWe uswe wantso canVisit we youchat uscan onin onchat ourYoutube Twitter! onGoogle+ Facebook! circles :) Sharing knowledge for a Books Authors Collaborators English Sign in better future Science Technology Economy Environment Humanities About Us Home André-Marie Ampère, "the Newton of Electricity" André-Marie Ampère, “the Newton of Electricity” Share 09 June 2017 Augusto Beléndez Sign in or register to rate this publication Full Professor of Applied Physics at the University On 24 November 1793, four years and a few months after the storming of the of Alicante (Spain) since Bastille, Jean-Jacques Ampère, a prosperous Lyon silk merchant linked to the Girondist 1996. [...] party, climbed the final steps to the scaffold. Arrested, tried and sentenced to capital 6 posts punishment, on that day he was guillotined, one more victim of the vagaries of the revolution. The death by guillotine of his father, to whom he was very strongly attached, had a profound affect on the young André-Marie Ampère (1775-1836), then 18 years old, plunging him into a deep depression that kept him isolated for several years on the Related articles family’s country estate, ten kilometers from Lyon. There, almost completely cut off from the outside world, almost like a person possessed, he devoured his father’s magnificent library. Newton and the Equations of Nature Ventana al Co… Astrophysics Faraday and the Electromagnetic Theory of Light Augusto Belé… Physics Faraday, the Apprentice Who Popularized Electricity Ventana al Co… Physics André-Marie Ampère was born on January 20, 1775 in Lyon. He was a prodigy child educated under the influence of the philosopher Rousseau / Wikipedia André-Marie Ampère was a child prodigy educated under the influence of the philosopher Rousseau, of whom his father was a fervent follower.