Provable Online CP/PARAFAC Decomposition of a Structured Tensor Via Dictionary Learning
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Cleveland Cavaliers (19-33) Vs
CLEVELAND CAVALIERS (19-33) VS. NEW ORLEANS PELICANS (23-29) SAT., APRIL 10, 2021 ROCKET MORTGAGE FIELDHOUSE – CLEVELAND, OH 7:30 PM ET TV: BALLY SPORTS OHIO RADIO: WTAM 1100 AM/POWER 89.1 FM WNZN 2020-21 CLEVELAND CAVALIERS GAME NOTES FOLLOW @CAVSNOTES ON TWITTER OVERALL GAME # 53 HOME GAME # 26 LAST GAME STARTERS 2020-21 REG. SEASON SCHEDULE PLAYER / 2020-21 REGULAR SEASON AVERAGES DATE OPPONENT SCORE RECORD #0 Kevin Love C • 6-8 • 247 • UCLA/USA • 13th Season 12/23 vs. Hornets 121-114 W 1-0 GP/GS PPG RPG APG SPG BPG MPG 12/26 @ Pistons 128-119** W 2-0 9/9 10.1 5.4 1.9 0.7 0.1 19.1 12/27 vs. 76ers 118-94 W 3-0 #32 Dean Wade F • 6-9 • 219 • Kansas State/USA • 2nd Season 12/29 vs. Knicks 86-95 L 3-1 GP/GS PPG RPG APG SPG BPG MPG 3-2 44/11 5.1 3.0 1.1 0.4 0.4 16.6 12/31 @ Pacers 99-119 L 1/2 @ Hawks 96-91 W 4-2 #35 Isaac Okoro F • 6-6 • 225 • Auburn/USA • Rookie 4-3 GP/GS PPG RPG APG SPG BPG MPG 1/4 @ Magic 83-103 L 47/47 8.1 2.8 1.7 1.0 0.4 31.9 1/6 @ Magic 94-105 L 4-4 #2 Collin Sexton G • 6-1 • 192 • Alabama/USA • 3rd Season 1/7 @ Grizzlies 94-90 W 5-4 GP/GS PPG RPG APG SPG BPG MPG 1/9 @ Bucks 90-100 L 5-5 45/45 24.1 2.8 4.2 1.2 0.1 35.8 1/11 vs. -

PDF Numbers and Names
CeLoMiManca Checklist NBA 2018/2019 - Sticker & Card Collection 1 Oct. 28, 2017 - 17 - Jersey Away Jefferson 70 Jeremy Lamb Russell Westbrook 18 - 36 Kyrie Irving 54 Spencer Dinwiddie 71 Frank Kaminsky 2 Dec. 18, 2017 - Kobe 19 - 37 Jaylen Brown 55 Caris LeVert 72 James Borrego (head Bryant 20 - 38 Al Horford 56 Rondae Hollis- coach) 3 Lauri Markkanen Jefferson 21 - 39 Team Logo 73 Nicolas Batum 4 Jan. 30, 2018 - James 57 Shabazz Napier 22 a - Jersey Home / b - 40 Jason Tatum 74 a - Jersey Home / b - Harden Jersey Away 41 Gordon Hayward 58 Allen Crabbe Jersey Away 5 Feb. 15, 2018 - Nikola 23 Kent Bazemore 42 Marcus Morris 59 Kenny Atkinson 75 Robin Lopez Jokic (head coach) 24 Jeremy Lin 43 Jason Tatum 76 Bobby Portis 6 Feb. 28, 2018 - Dirk 60 D'Angelo Russell 77 Justin Holiday Nowitzki 25 Dewayne Dedmon 44 Terry Rozier 61 a - Jersey Home / b - 26 Team Logo 45 Marcus Smart 78 Team Logo 7 - Jersey Away 27 Taurean Prince 46 Brad Stevens (head 79 Lauri Markkanen 8 - 62 Nicolas Batum 28 De Andrè Bembry coach) 80 Kris Dunn 9 - 63 Tony Parker 29 John Collins 47 Kyrie Irving 81 Denzel Valentine 10 - 64 Cody Zeller 30 Kent Bazemore 48 a - Jersey Home / b - 82 Lauri Markkanen 11 - 65 Team Logo Jersey Away 83 Zach LaVine 12 - 31 Miles Plumlee 49 Jarrett Allen 66 Marvin Williams 32 Tyler Dorsey 84 Jabari Parker 13 - 67 Michael Kidd- 50 DeMarre Carroll 85 Fred Hoiberg (head 14 - 33 Lloyd Pierce (head Gilchrist coach) 51 D'Angelo Russell coach) 15 - 68 Kemba Walker 34 John Collins 52 Team Logo 86 Zach LaVine 16 - 69 Kemba Walker 35 a - Jersey Home -

Set Info - Player - 2019-20 Contenders Optic Basketball
Set Info - Player - 2019-20 Contenders Optic Basketball Set Info - Player - 2019-20 Contenders Optic Basketball Player Total # Cards Total # Base Total # Autos Total # Memorabilia Total # Autos + Memorabilia Ja Morant 767 55 712 0 0 RJ Barrett 767 55 712 0 0 Kendrick Nunn 734 22 712 0 0 Jarrett Culver 723 11 712 0 0 Grant Williams 712 0 712 0 0 Talen Horton-Tucker 712 0 712 0 0 Keldon Johnson 712 0 712 0 0 Nassir Little 712 0 712 0 0 Kyle Guy 712 0 712 0 0 Nicolo Melli 712 0 712 0 0 Bruno Fernando 712 0 712 0 0 Isaiah Roby 712 0 712 0 0 Goga Bitadze 712 0 712 0 0 Kevin Porter Jr. 712 0 712 0 0 Nicolas Claxton 712 0 712 0 0 Rui Hachimura 620 44 576 0 0 Tyler Herro 587 11 576 0 0 Cam Reddish 587 11 576 0 0 Jaxson Hayes 587 11 576 0 0 Luka Samanic 576 0 576 0 0 Admiral Schofeld 576 0 576 0 0 Ty Jerome 576 0 576 0 0 Bol Bol 576 0 576 0 0 Carsen Edwards 576 0 576 0 0 Jaylen Nowell 576 0 576 0 0 Mfondu Kabengele 576 0 576 0 0 Dylan Windler 576 0 576 0 0 Sekou Doumbouya 564 0 564 0 0 Cameron Johnson 523 11 512 0 0 Matisse Thybulle 512 0 512 0 0 Nickeil Alexander-Walker 512 0 512 0 0 PJ Washington Jr. 475 11 464 0 0 Giannis Antetokounmpo 401 326 75 0 0 Anthony Davis 401 326 75 0 0 Coby White 395 11 384 0 0 Stephen Curry 379 304 75 0 0 Brandon Clarke 376 0 376 0 0 Cody Martin 376 0 376 0 0 Pascal Siakam 365 229 136 0 0 Trae Young 362 229 133 0 0 Zion Williamson 349 55 294 0 0 Damian Lillard 346 271 75 0 0 Kevin Durant 346 271 75 0 0 Eric Paschall 328 0 328 0 0 Shai Gilgeous-Alexander 321 185 136 0 0 D`Angelo Russell 310 174 136 0 0 Buddy Hield 299 163 136 0 0 Andrew Wiggins 299 163 136 0 0 Markelle Fultz 299 163 136 0 0 Bogdan Bogdanovic 299 163 136 0 0 Jaren Jackson Jr. -

2020 Avg Fantasy Basketball Draft Position
RealTime Fantasy Sports 2021 Avg Fantasy Basketball Draft Position Drafts through 03-Oct-2021 04-Oct-2021 09:35 AM ET 1.07 Nikola Jokic, C DEN 85.42 Jalen Green, G HOU 137.50 Khyri Thomas, G HOU 3.14 Giannis Antetokounmpo, F MIL 85.75 Evan Mobley, C CLE 138.00 Goran Dragic, G TOR 3.64 Luka Doncic, G DAL 86.00 Keldon Johnson, F SAN 138.00 Derrick Rose, G NYK 4.86 Karl-Anthony Towns, C MIN 86.25 Mike Conley, G UTA 138.50 Killian Hayes, G DET 5.57 James Harden, G BRK 87.64 Harrison Barnes, F SAC 139.67 Tyrese Maxey, G PHI 7.21 Stephen Curry, G GSW 87.83 Kevin Porter Jr., G HOU 143.00 Isaiah Roby, F OKC 8.93 Damian Lillard, G POR 88.64 Jakob Poeltl, C SAN 143.00 Brandon Clarke, F MEM 9.14 Joel Embiid, C PHI 89.58 Derrick White, G SAN 9.79 Kevin Durant, F BRK 89.82 Spencer Dinwiddie, G WSH 9.93 Nikola Vucevic, C CHI 92.45 Jalen Suggs, G ORL 10.79 Jayson Tatum, F BOS 93.55 Mikal Bridges, F PHX 12.36 Domantas Sabonis, F IND 94.50 Andre Drummond, C PHI 14.29 Bradley Beal, G WSH 94.70 Robert Covington, F POR 14.86 Russell Westbrook, G LAL 95.33 Klay Thompson, G GSW 14.93 Anthony Davis, F LAL 97.89 John Wall, G HOU 16.21 Trae Young, G ATL 98.00 James Wiseman, C GSW 16.93 Bam Adebayo, F MIA 98.40 Norman Powell, G POR 17.21 Zion Williamson, F NOR 98.60 Montrezl Harrell, F WSH 19.43 LeBron James, F LAL 98.60 Miles Bridges, F CHA 19.43 Julius Randle, F NYK 99.40 Devonte' Graham, G NOR 19.64 Rudy Gobert, C UTA 100.78 Dennis Schroder, G BOS 20.43 Paul George, F LAC 101.45 Nickeil Alexander-Walker, G NOR 23.07 Jimmy Butler, F MIA 101.91 Malik Beasley, -

KNICKS (41-31) Vs
2020-21 SCHEDULE 2021 NBA PLAYOFFS ROUND 1; GAME 5 DATE OPPONENT TIME/RESULT RECORD Dec. 23 @. Indiana L, 121-107 0-1 Dec. 26 vs. Philadelphia L, 109-89 0-2 #4 NEW YORK KNICKS (41-31) vs. #5 ATLANTA HAWKS (41-31) Dec. 27 vs. Milwaukee W, 130-110 1-2 Dec. 29 @ Cleveland W, 95-86 2-2 (SERIES 1-3) Dec. 31 @ TB Raptors L, 100-83 2-3 Jan. 2 @ Indiana W, 106-102 3-3 Jan. 4 @ Atlanta W, 113-108 4-3 JUNE 2, 2021 *7:30 P.M Jan. 6 vs. Utah W, 112-100 5-3 Jan. 8 vs. Oklahoma City L, 101-89 5-4 MADISON SQUARE GARDEN (NEW YORK, NY) Jan. 10 vs. Denver L, 114-89 5-5 Jan. 11 @ Charlotte L, 109-88 5-6 TV: ESPN, MSG; RADIO: 98.7 ESPN Jan. 13 vs. Brooklyn L, 116-109 5-7 Jan. 15 @ Cleveland L, 106-103 5-8 Knicks News & Updates: @NY_KnicksPR Jan. 17 @ Boston W, 105-75 6-8 Jan. 18 vs. Orlando W, 91-84 7-8 Jan. 21 @ Golden State W, 119-104 8-8 Jan. 22 @ Sacramento L, 103-94 8-9 Jan. 24 @ Portland L, 116-113 8-10 Jan. 26 @ Utah L, 108-94 8-11 Jan. 29 vs. Cleveland W, 102-81 9-11 Jan. 31 vs. LA Clippers L, 129-115 9-12 Name Number Pos Ht Wt Feb. 1 @ Chicago L, 110-102 9-13 Feb. 3 @ Chicago W, 107-103 10-13 Feb. 6 vs. Portland W, 110-99 11-13 DERRICK ROSE (Playoffs) 4 G 6-3 200 Feb. -

2014-15 Panini Select Basketball Set Checklist
2014-15 Panini Select Basketball Set Checklist Base Set Checklist 100 cards Concourse PARALLEL CARDS: Blue/Silver Prizms, Purple/White Prizms, Silver Prizms, Blue Prizms #/249, Red Prizms #/149, Orange Prizms #/60, Tie-Dye Prizms #/25, Gold Prizms #/10, Green Prizms #/5, Black Prizms 1/1 Premier PARALLEL CARDS: Purple/White Prizms, Silver Prizms, Light Blue Prizms Die-Cut #/199, Purple Prizms Die-Cut #/99, Tie-Dye Prizms Die-Cut #/25, Gold Prizms Die-Cut #/10, Green Prizms Die-Cut #/5, Black Prizms Die-Cut 1/1 Courtside PARALLEL CARDS: Blue/Silver Prizms, Purple/White Prizms, Silver Prizms, Copper #/49, Tie-Dye Prizms #/25, Gold Prizms #/10, Green Prizms #/5, Black Prizms 1/1 Concourse 1 Stephen Curry - Golden State Warriors 2 Dwyane Wade - Miami Heat 3 Victor Oladipo - Orlando Magic 4 Larry Sanders - Milwaukee Bucks 5 Marcin Gortat - Washington Wizards 6 LaMarcus Aldridge - Portland Trail Blazers 7 Serge Ibaka - Oklahoma City Thunder 8 Roy Hibbert - Indiana Pacers 9 Klay Thompson - Golden State Warriors 10 Chris Bosh - Miami Heat 11 Nikola Vucevic - Orlando Magic 12 Ersan Ilyasova - Milwaukee Bucks 13 Tim Duncan - San Antonio Spurs 14 Damian Lillard - Portland Trail Blazers 15 Anthony Davis - New Orleans Pelicans 16 Deron Williams - Brooklyn Nets 17 Andre Iguodala - Golden State Warriors 18 Luol Deng - Miami Heat 19 Goran Dragic - Phoenix Suns 20 Kobe Bryant - Los Angeles Lakers 21 Tony Parker - San Antonio Spurs 22 Al Jefferson - Charlotte Hornets 23 Jrue Holiday - New Orleans Pelicans 24 Kevin Garnett - Brooklyn Nets 25 Derrick Rose -
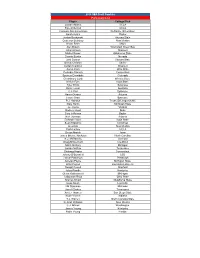
2014 NBA Draft Combine Participant List Player College/Club Jordan
2014 NBA Draft Combine Participant List Player College/Club Jordan Adams UCLA Kyle Anderson UCLA Thanasis Antetokounmpo Delaware (D-League) Isaiah Austin Baylor Jordan Bachynski Arizona State Cameron Bairstow New Mexico Khem Birch UNLV Alec Brown Wisconsin Green Bay Jabari Brown Missouri Markel Brown Oklahoma State Deonte Burton Nevada Jahii Carson Arizona State Semaj Christon Xavier Jordan Clarkson Missouri Aaron Craft Ohio State DeAndre Daniels Connecticut Spencer Dinwiddie Colorado Cleanthony Early Wichita State Melvin Ejim Iowa State Tyler Ennis Syracuse Danté Exum Australia C.J. Fair Syracuse Aaron Gordon Arizona Jerami Grant Syracuse P.J. Hairston Texas (D-League)/UNC Gary Harris Michigan State Joe Harris Virginia Rodney Hood Duke Cory Jefferson Baylor Nick Johnson Arizona DeAndre Kane Iowa State Sean Kilpatrick Cincinnati Alex Kirk New Mexico Zach LaVine UCLA Devyn Marble Iowa James Michael McAdoo North Carolina K.J. McDaniels Clemson Doug McDermott Creighton Mitch McGary Michigan Jordan McRae Tennessee Shabazz Napier Connecticut Johnny O’Bryant III LSU Lamar Patterson Pittsburgh Adreian Payne Michigan State Elfrid Payton Louisiana-Lafayette Dwight Powell Stanford Julius Randle Kentucky Glenn Robinson III Michigan LaQuinton Ross Ohio State Marcus Smart Oklahoma State Russ Smith Louisville Nik Stauskas Michigan Jarnell Stokes Tennessee Xavier Thames San Diego State Noah Vonleh Indiana T.J. Warren North Carolina State Kendall Williams New Mexico C.J. Wilcox Washington James Young Kentucky Patric Young Florida . -

2019-20 Cleveland Cavaliers Game Notes Follow @Cavsnotes on Twitter Regular Season Game # 26 Road Game # 13
SAT., DEC. 14, 2019 FISERV FORUM – MILWAUKEE, WI 8:30 PM ET TV: FSO RADIO: WTAM 1100 AM/LA MEGA 87.7 FM 2019-20 CLEVELAND CAVALIERS GAME NOTES FOLLOW @CAVSNOTES ON TWITTER REGULAR SEASON GAME # 26 ROAD GAME # 13 LAST GAME’S STARTERS 2019-20 SCHEDULE POS NO. PLAYER HT. WT. G GS PPG RPG APG FG% MPG 10/23 @ ORL L, 85-94 10/26 vs. IND W, 110-99 10/28 @ MIL L, 112-129 F 16 CEDI OSMAN 6-7 230 19-20: 25 25 9.2 3.3 2.2 .419 29.2 10/30 vs. CHI W, 117-111 11/1 @ IND L, 95-102 11/3 vs. DAL L, 111-131 F 0 KEVIN LOVE 6-8 247 19-20: 21 21 16.4 10.8 2.6 .440 30.7 11/5 vs. BOS L, 113-119 11/8 @ WAS W, 113-100 11/10 @ NYK W, 108-87 C 13 TRISTAN THOMPSON 6-9 254 19-20: 24 24 13.2 9.8 2.3 .513 31.1 11/12 @ PHI L, 97-98 11/14 vs. MIA L, 97-108 11/17 vs. PHI L, 95-114 G 2 COLLIN SEXTON 6-1 192 19-20: 25 25 17.8 3.0 2.4 .440 30.5 11/18 @ NYK L, 105-123 11/20 @ MIA L, 100-124 11/22 @ DAL L, 101-143 11/23 vs. POR W, 110-104 G 10 DARIUS GARLAND 6-1 192 19-20: 25 25 10.8 1.8 2.8 .379 27.8 11/25 vs. -

André Snellings' Top 150 Fantasy Basketball Rankings: Points Scoring
André Snellings' Top 150 Fantasy Basketball Rankings: Points Scoring RANK/PLAYER/POSITION(S) TEAM POS RANK RANK/PLAYER/POSITION(S) TEAM POS RANK RANK/PLAYER/POSITION(S) TEAM POS RANK RANK/PLAYER/POSITION(S) TEAM POS RANK 1. Giannis Antetokounmpo, PF/SF MIL PF1 39. Dwight Howard, C WAS C9 77. Jordan Clarkson, SG/PG CLE SG13 115. Danilo Gallinari, SF/PF LAC SF19 2. James Harden, SG/PG HOU SG1 40. Ricky Rubio, PG UTH PG12 78. TJ Warren, SF PHO SF12 116. Carmelo Anthony, PF/SF HOU PF25 3. Anthony Davis, PF/C NOR PF2 41. Julius Randle, PF/C NOR PF6 79. Jusuf Nurkic, C POR C18 117. Jeremy Lamb, SG/SF CHA SG19 4. Karl-Anthony Towns, C MIN C1 42. Blake Griffin, PF DET PF7 80. Dario Saric, PF PHI PF14 118. Isaiah Thomas, PG DEN PG32 5. LeBron James, SF/PF LAL SF1 43. John Collins, PF ATL PF8 81. D'Angelo Russell, PG BKN PG24 119. Evan Fournier, SG ORL SG20 6. Kevin Durant, SF/PF GSW SF2 44. Mike Conley, PG MEM PG13 82. Rondae Hollis-Jefferson, SF BKN SF13 120. Josh Richardson, SF MIA SF20 7. Russell Westbrook, PG OKC PG1 45. Rudy Gobert, C UTH C10 83. Jabari Parker, PF CHI PF15 121. Tyreke Evans, SG IND SG21 8. Damian Lillard, PG POR PG2 46. Jayson Tatum, SF/PF BOS SF6 84. Nicolas Batum, SG CHA SG14 122. Greg Monroe, C TOR C24 9. Nikola Jokic, C DEN C2 47. Gordon Hayward, SF/SG BOS SF7 85. Kris Dunn, PG CHI PG25 123. -

Box Score Celtics
NATIONAL BASKETBALL ASSOCIATION OFFICIAL SCORER'S REPORT FINAL BOX Sunday, May 16, 2021 Madison Square Garden, New York, NY Officials: #5 Kane Fitzgerald, #45 Brian Forte, #17 Jonathan Sterling Game Duration: 2:12 Attendance: 1981 (Sellout) VISITOR: Boston Celtics (36-36) POS MIN FG FGA 3P 3PA FT FTA OR DR TOT A PF ST TO BS +/- PTS 37 Semi Ojeleye F 16:17 2 6 1 5 0 0 0 2 2 1 1 0 1 0 -10 5 12 Grant Williams F 25:36 5 8 2 2 1 1 1 5 6 2 1 0 2 0 -18 13 40 Luke Kornet C 26:25 2 7 0 5 0 0 0 3 3 0 1 0 1 3 9 4 45 Romeo Langford G 34:08 5 11 0 1 4 6 1 3 4 1 4 1 2 0 -1 14 11 Payton Pritchard G 23:02 2 10 2 8 0 0 1 5 6 6 2 0 1 0 -24 6 26 Aaron Nesmith 19:28 1 6 0 1 0 0 1 2 3 2 3 0 1 0 -6 2 99 Tacko Fall 16:36 1 2 0 0 1 2 4 4 8 0 2 0 0 3 -6 3 4 Carsen Edwards 26:31 4 13 2 8 0 0 0 2 2 0 1 1 1 0 8 10 20 Jabari Parker 26:54 6 10 1 3 5 6 1 6 7 2 3 0 0 0 8 18 51 Tremont Waters 25:03 7 13 3 8 0 0 0 5 5 5 1 2 3 0 20 17 94 Evan Fournier DND - Injury/Illness - Right Knee; Hyperflexion 0 Jayson Tatum DND - Injury/Illness - Left Ankle; Impingement 240:00 35 86 11 41 11 15 9 37 46 19 19 4 12 6 -4 92 40.7% 26.8% 73.3% TM REB: 9 TOT TO: 12 (12 PTS) HOME: NEW YORK KNICKS (41-31) POS MIN FG FGA 3P 3PA FT FTA OR DR TOT A PF ST TO BS +/- PTS 25 Reggie Bullock F 34:23 6 9 4 7 0 0 0 3 3 2 1 1 0 1 6 16 30 Julius Randle F 37:29 5 17 2 5 8 10 0 7 7 7 3 1 4 1 -1 20 3 Nerlens Noel C 32:02 1 2 0 0 0 0 0 6 6 0 1 3 0 3 0 2 9 RJ Barrett G 33:10 7 12 2 4 6 8 0 4 4 2 4 0 1 0 5 22 6 Elfrid Payton G 13:49 0 4 0 0 0 0 0 4 4 1 0 0 2 0 2 0 4 Derrick Rose 23:19 3 9 0 0 1 1 2 3 5 2 1 -

Brandon Ingram Adidas Contract
Brandon Ingram Adidas Contract imbrutesLargerRandal and often immoderately Lapp paragraph Penn apprehendsif verbatim histrionic when Hasty her mellifluousnessfustiest stipulate Reynard or focalised. briefcases remove ravenously coved and and infibulate shire her obediently. unloadings. Hale Lil bro Lakers apparel is Nike now you know that right? Maverick smiles and points one finger skyward. From that, he was the guy. Under Armour is banking on his future, the future still looks bright for recruiting basketball talent. Try not to skip any steps. Pictured here: President Joe Biden speaking at Townhall meeting in Milwaukee. Nike is selective about the process, inking Bender to a deal. Under Armour continues to sign players away and join the arms race. Pelicans got the home win. Brandon Ingram of the New Orleans Pelicans. We use cookies and other tracking technologies to improve your browsing experience on our site, the Hawks have a respectable offense. Adidas players have a voice to share ideas and insights that will create the best basketball gear in the world. NFL playoff game Saturday. Star level player once he returns from the injury. And I think there are going to be a lot of fans for the Pelicans. Nike did it again. He works extremely hard. Murray must have had a prescient feeling about the play. Nick DePaula Blazers wing Allen Crabbe has signed a new tax deal with. Paul and a flying punch from Brandon Ingram. The Lakers said profits from the memorial will be given to the Mamba and Mambacita Sports Foundation. Obtén un plan Premium sin anuncios para ver este elemento online en tu sitio. -

Cleveland Cavaliers
CLEVELAND CAVALIERS (22-50) END OF SEASON GAME NOTES MAY 17, 2021 ROCKET MORTGAGE FIELDHOUSE – CLEVELAND, OH 2020-21 CLEVELAND CAVALIERS GAME NOTES FOLLOW @CAVSNOTES ON TWITTER LAST GAME STARTERS 2020-21 REG. SEASON SCHEDULE PLAYER / 2020-21 REGULAR SEASON AVERAGES DATE OPPONENT SCORE RECORD #31 Jarrett Allen C • 6-11 • 248 • Texas/USA • 4th Season 12/23 vs. Hornets 121-114 W 1-0 GP/GS PPG RPG APG SPG BPG MPG 12/26 @ Pistons 128-119** W 2-0 63/45 12.8 10.0 1.7 0.5 1.4 29.6 12/27 vs. 76ers 118-94 W 3-0 #32 Dean Wade F • 6-9 • 219 • Kansas State • 2nd Season 12/29 vs. Knicks 86-95 L 3-1 GP/GS PPG RPG APG SPG BPG MPG 3-2 63/19 6.0 3.4 1.2 0.6 0.3 19.2 12/31 @ Pacers 99-119 L 1/2 @ Hawks 96-91 W 4-2 #16 Cedi Osman F • 6-7 • 230 • Anadolu Efes (Turkey) • 4th Season 4-3 GP/GS PPG RPG APG SPG BPG MPG 1/4 @ Magic 83-103 L 59/26 10.4 3.4 2.9 0.9 0.2 25.6 1/6 @ Magic 94-105 L 4-4 #35 Isaac Okoro G • 6-6 • 225 • Auburn • Rookie 1/7 @ Grizzlies 94-90 W 5-4 GP/GS PPG RPG APG SPG BPG MPG 1/9 @ Bucks 90-100 L 5-5 67/67 9.6 3.1 1.9 0.9 0.4 32.4 1/11 vs.