Cevians, Symmedians, and Excircles
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Some Concurrencies from Tucker Hexagons
Forum Geometricorum b Volume 2 (2002) 5–13. bbb FORUM GEOM ISSN 1534-1178 Some Concurrencies from Tucker Hexagons Floor van Lamoen Abstract. We present some concurrencies in the figure of Tucker hexagons to- gether with the centers of their Tucker circles. To find the concurrencies we make use of extensions of the sides of the Tucker hexagons, isosceles triangles erected on segments, and special points defined in some triangles. 1. The Tucker hexagon Tφ and the Tucker circle Cφ Consider a scalene (nondegenerate) reference triangle ABC in the Euclidean plane, with sides a = BC, b = CA and c = AB. Let Ba be a point on the sideline CA. Let Ca be the point where the line through Ba antiparallel to BC meets AB. Then let Ac be the point where the line through Ca parallel to CA meets BC. Continue successively the construction of parallels and antiparallels to complete a hexagon BaCaAcBcCbAb of which BaCa, AcBc and CbAb are antiparallel to sides BC, CA and AB respectively, while BcCb, AcCa and AbBa are parallel to these respective sides. B Cb K Ab B T K Ac Ca KC KA C Bc Ba A Figure 1 This is the well known way to construct a Tucker hexagon. Each Tucker hexagon is circumscribed by a circle, the Tucker circle. The three antiparallel sides are congruent; their midpoints KA, KB and KC lie on the symmedians of ABC in such a way that AKA : AK = BKB : BK = CKC : CK, where K denotes the symmedian point. See [1, 2, 3]. 1.1. Identification by central angles. -

Relationships Between Six Excircles
Sangaku Journal of Mathematics (SJM) c SJM ISSN 2534-9562 Volume 3 (2019), pp.73-90 Received 20 August 2019. Published on-line 30 September 2019 web: http://www.sangaku-journal.eu/ c The Author(s) This article is published with open access1. Relationships Between Six Excircles Stanley Rabinowitz 545 Elm St Unit 1, Milford, New Hampshire 03055, USA e-mail: [email protected] web: http://www.StanleyRabinowitz.com/ Abstract. If P is a point inside 4ABC, then the cevians through P divide 4ABC into smaller triangles of various sizes. We give theorems about the rela- tionship between the radii of certain excircles of some of these triangles. Keywords. Euclidean geometry, triangle geometry, excircles, exradii, cevians. Mathematics Subject Classification (2010). 51M04. 1. Introduction Let P be any point inside a triangle ABC. The cevians through P divide 4ABC into six smaller triangles. In a previous paper [5], we found relationships between the radii of the circles inscribed in these triangles. For example, if P is at the orthocenter H, as shown in Figure 1, then we found that r1r3r5 = r2r4r6, where the ri are radii of the incircles as shown in the figure. arXiv:1910.00418v1 [math.HO] 28 Sep 2019 Figure 1. r1r3r5 = r2r4r6 In this paper, we will find similar results using excircles instead of incircles. When the cevians through a point P interior to a triangle ABC are drawn, many smaller 1This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited. -

Investigating Centers of Triangles: the Fermat Point
Investigating Centers of Triangles: The Fermat Point A thesis submitted to the Miami University Honors Program in partial fulfillment of the requirements for University Honors with Distinction by Katherine Elizabeth Strauss May 2011 Oxford, Ohio ABSTRACT INVESTIGATING CENTERS OF TRIANGLES: THE FERMAT POINT By Katherine Elizabeth Strauss Somewhere along their journey through their math classes, many students develop a fear of mathematics. They begin to view their math courses as the study of tricks and often seemingly unsolvable puzzles. There is a demand for teachers to make mathematics more useful and believable by providing their students with problems applicable to life outside of the classroom with the intention of building upon the mathematics content taught in the classroom. This paper discusses how to integrate one specific problem, involving the Fermat Point, into a high school geometry curriculum. It also calls educators to integrate interesting and challenging problems into the mathematics classes they teach. In doing so, a teacher may show their students how to apply the mathematics skills taught in the classroom to solve problems that, at first, may not seem directly applicable to mathematics. The purpose of this paper is to inspire other educators to pursue similar problems and investigations in the classroom in order to help students view mathematics through a more useful lens. After a discussion of the Fermat Point, this paper takes the reader on a brief tour of other useful centers of a triangle to provide future researchers and educators a starting point in order to create relevant problems for their students. iii iv Acknowledgements First of all, thank you to my advisor, Dr. -

Special Isocubics in the Triangle Plane
Special Isocubics in the Triangle Plane Jean-Pierre Ehrmann and Bernard Gibert June 19, 2015 Special Isocubics in the Triangle Plane This paper is organized into five main parts : a reminder of poles and polars with respect to a cubic. • a study on central, oblique, axial isocubics i.e. invariant under a central, oblique, • axial (orthogonal) symmetry followed by a generalization with harmonic homolo- gies. a study on circular isocubics i.e. cubics passing through the circular points at • infinity. a study on equilateral isocubics i.e. cubics denoted 60 with three real distinct • K asymptotes making 60◦ angles with one another. a study on conico-pivotal isocubics i.e. such that the line through two isoconjugate • points envelopes a conic. A number of practical constructions is provided and many examples of “unusual” cubics appear. Most of these cubics (and many other) can be seen on the web-site : http://bernard.gibert.pagesperso-orange.fr where they are detailed and referenced under a catalogue number of the form Knnn. We sincerely thank Edward Brisse, Fred Lang, Wilson Stothers and Paul Yiu for their friendly support and help. Chapter 1 Preliminaries and definitions 1.1 Notations We will denote by the cubic curve with barycentric equation • K F (x,y,z) = 0 where F is a third degree homogeneous polynomial in x,y,z. Its partial derivatives ∂F ∂2F will be noted F ′ for and F ′′ for when no confusion is possible. x ∂x xy ∂x∂y Any cubic with three real distinct asymptotes making 60◦ angles with one another • will be called an equilateral cubic or a 60. -

Orthocorrespondence and Orthopivotal Cubics
Forum Geometricorum b Volume 3 (2003) 1–27. bbb FORUM GEOM ISSN 1534-1178 Orthocorrespondence and Orthopivotal Cubics Bernard Gibert Abstract. We define and study a transformation in the triangle plane called the orthocorrespondence. This transformation leads to the consideration of a fam- ily of circular circumcubics containing the Neuberg cubic and several hitherto unknown ones. 1. The orthocorrespondence Let P be a point in the plane of triangle ABC with barycentric coordinates (u : v : w). The perpendicular lines at P to AP , BP, CP intersect BC, CA, AB respectively at Pa, Pb, Pc, which we call the orthotraces of P . These orthotraces 1 lie on a line LP , which we call the orthotransversal of P . We denote the trilinear ⊥ pole of LP by P , and call it the orthocorrespondent of P . A P P ∗ P ⊥ B C Pa Pc LP H/P Pb Figure 1. The orthotransversal and orthocorrespondent In barycentric coordinates, 2 ⊥ 2 P =(u(−uSA + vSB + wSC )+a vw : ··· : ···), (1) Publication Date: January 21, 2003. Communicating Editor: Paul Yiu. We sincerely thank Edward Brisse, Jean-Pierre Ehrmann, and Paul Yiu for their friendly and valuable helps. 1The homography on the pencil of lines through P which swaps a line and its perpendicular at P is an involution. According to a Desargues theorem, the points are collinear. 2All coordinates in this paper are homogeneous barycentric coordinates. Often for triangle cen- ters, we list only the first coordinate. The remaining two can be easily obtained by cyclically permut- ing a, b, c, and corresponding quantities. Thus, for example, in (1), the second and third coordinates 2 2 are v(−vSB + wSC + uSA)+b wu and w(−wSC + uSA + vSB )+c uv respectively. -

Generalized Gergonne and Nagel Points
Generalized Gergonne and Nagel Points B. Odehnal June 16, 2009 Abstract In this paper we show that the Gergonne point G of a triangle ∆ in the Euclidean plane can in fact be seen from the more general point of view, i.e., from the viewpoint of projective geometry. So it turns out that there are up to four Gergonne points associated with ∆. The Gergonne and Nagel point are isotomic conjugates of each other and thus we find up to four Nagel points associated with a generic triangle. We reformulate the problems in a more general setting and illustrate the different appearances of Gergonne points in different affine geometries. Darboux’s cubic can also be found in the more general setting and finally a projective version of Feuerbach’s circle appears. Mathematics Subject Classification (2000): 51M04, 51M05, 51B20 Key Words: triangle, incenter, excenters, Gergonne point, Brianchon’s theorem, Nagel point, isotomic conjugate, Darboux’s cubic, Feuerbach’s nine point circle. 1 Introduction Assume ∆ = {A,B,C} is a triangle with vertices A, B, and C and the incircle i. Gergonne’s point is the locus of concurrency of the three cevians connecting the contact points of i and ∆ with the opposite vertices. The Gergonne point, which can also be labelled with X7 according to [10, 11] has frequently attracted mathematician’s interest. Some generalizations have been given. So, for example, one can replace the incircle with a concentric 1 circle and replace the contact points of the incircle and the sides of ∆ with their reflections with regard to the incenter as done in [2]. -

Cevians, Symmedians, and Excircles Cevian Cevian Triangle & Circle
10/5/2011 Cevians, Symmedians, and Excircles MA 341 – Topics in Geometry Lecture 16 Cevian A cevian is a line segment which joins a vertex of a triangle with a point on the opposite side (or its extension). B cevian C A D 05-Oct-2011 MA 341 001 2 Cevian Triangle & Circle • Pick P in the interior of ∆ABC • Draw cevians from each vertex through P to the opposite side • Gives set of three intersecting cevians AA’, BB’, and CC’ with respect to that point. • The triangle ∆A’B’C’ is known as the cevian triangle of ∆ABC with respect to P • Circumcircle of ∆A’B’C’ is known as the evian circle with respect to P. 05-Oct-2011 MA 341 001 3 1 10/5/2011 Cevian circle Cevian triangle 05-Oct-2011 MA 341 001 4 Cevians In ∆ABC examples of cevians are: medians – cevian point = G perpendicular bisectors – cevian point = O angle bisectors – cevian point = I (incenter) altitudes – cevian point = H Ceva’s Theorem deals with concurrence of any set of cevians. 05-Oct-2011 MA 341 001 5 Gergonne Point In ∆ABC find the incircle and points of tangency of incircle with sides of ∆ABC. Known as contact triangle 05-Oct-2011 MA 341 001 6 2 10/5/2011 Gergonne Point These cevians are concurrent! Why? Recall that AE=AF, BD=BF, and CD=CE Ge 05-Oct-2011 MA 341 001 7 Gergonne Point The point is called the Gergonne point, Ge. Ge 05-Oct-2011 MA 341 001 8 Gergonne Point Draw lines parallel to sides of contact triangle through Ge. -

On the Standard Lengths of Angle Bisectors and the Angle Bisector Theorem
Global Journal of Advanced Research on Classical and Modern Geometries ISSN: 2284-5569, pp.15-27 ON THE STANDARD LENGTHS OF ANGLE BISECTORS AND THE ANGLE BISECTOR THEOREM G.W INDIKA SHAMEERA AMARASINGHE ABSTRACT. In this paper the author unveils several alternative proofs for the standard lengths of Angle Bisectors and Angle Bisector Theorem in any triangle, along with some new useful derivatives of them. 2010 Mathematical Subject Classification: 97G40 Keywords and phrases: Angle Bisector theorem, Parallel lines, Pythagoras Theorem, Similar triangles. 1. INTRODUCTION In this paper the author introduces alternative proofs for the standard length of An- gle Bisectors and the Angle Bisector Theorem in classical Euclidean Plane Geometry, on a concise elementary format while promoting the significance of them by acquainting some prominent generalized side length ratios within any two distinct triangles existed with some certain correlations of their corresponding angles, as new lemmas. Within this paper 8 new alternative proofs are exposed by the author on the angle bisection, 3 new proofs each for the lengths of the Angle Bisectors by various perspectives with also 5 new proofs for the Angle Bisector Theorem. 1.1. The Standard Length of the Angle Bisector Date: 1 February 2012 . 15 G.W Indika Shameera Amarasinghe The length of the angle bisector of a standard triangle such as AD in figure 1.1 is AD2 = AB · AC − BD · DC, or AD2 = bc 1 − (a2/(b + c)2) according to the standard notation of a triangle as it was initially proved by an extension of the angle bisector up to the circumcircle of the triangle. -
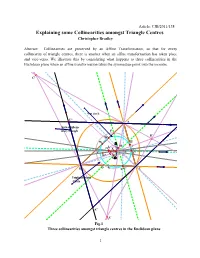
Explaining Some Collinearities Amongst Triangle Centres Christopher Bradley
Article: CJB/2011/138 Explaining some Collinearities amongst Triangle Centres Christopher Bradley Abstract: Collinearities are preserved by an Affine Transformation, so that for every collinearity of triangle centres, there is another when an affine transformation has taken place and vice-versa. We illustrate this by considering what happens to three collinearities in the Euclidean plane when an affine transformation takes the symmedian point into the incentre. C' 9 pt circle C'' A B'' Anticompleme ntary triangle F B' W' W E' L M V O X Z E F' K 4 V' K'' Y G T H N' D B U D'U' C Triplicate ratio Circle A'' A' Fig.1 Three collinearities amongst triangle centres in the Euclidean plane 1 1. When the circumconic, the nine-point conic, the triplicate ratio conic and the 7 pt. conic are all circles The condition for this is that the circumconic is a circle and then the tangents at A, B, C form a triangle A'B'C' consisting of the ex-symmedian points A'(– a2, b2, c2) and similarly for B', C' by appropriate change of sign and when this happen AA', BB', CC' are concurrent at the symmedian point K(a2, b2, c2). There are two very well-known collinearities and one less well-known, and we now describe them. First there is the Euler line containing amongst others the circumcentre O with x-co-ordinate a2(b2 + c2 – a2), the centroid G(1, 1, 1), the orthocentre H with x-co-ordinate 1/(b2 + c2 – a2) and T, the nine-point centre which is the midpoint of OH. -

Nagel , Speiker, Napoleon, Torricelli
Nagel , Speiker, Napoleon, Torricelli MA 341 – Topics in Geometry Lecture 17 Centroid The point of concurrency of the three medians. 07-Oct-2011 MA 341 2 Circumcenter Point of concurrency of the three perpendicular bisectors. 07-Oct-2011 MA 341 3 Orthocenter Point of concurrency of the three altitudes. 07-Oct-2011 MA 341 4 Incenter Point of concurrency of the three angle bisectors. 07-Oct-2011 MA 341 5 Symmedian Point Point of concurrency of the three symmedians. 07-Oct-2011 MA 341 6 Gergonne Point Point of concurrency of the three segments from vertices to intangency points. 07-Oct-2011 MA 341 7 Spieker Point The Spieker point is the incenter of the medial triangle. 07-Oct-2011 MA 341 8 Nine Point Circle Center The 9 point circle center is midpoint of the Euler segment. 07-Oct-2011 MA 341 9 Mittenpunkt Point The mittenpunkt of ΔABC is the symmedian point of the excentral triangle 05-Oct-2011 MA 341 001 10 Nagel Point Nagel point = point of concurrency of cevians to points of tangency of excircles 05-Oct-2011 MA 341 001 11 Nagel Point 05-Oct-2011 MA 341 001 12 The Nagel Point Ea has the unique property of being the point on the perimeter that is exactly half way around the triangle from A. = AB+BEaa AC+CE =s Then =- =- =- =- BEaa s AB s c and CE s AC s b BE sc- a = - CEa s b 07-Oct-2011 MA 341 13 The Nagel Point Likewise CE sa- b = - AEb s c AE sb- c = - BEc s a Apply Ceva’s Theorem AE BE CE sbscsa--- cab=´´=1 --- BEcab CE AE s a s b s c 07-Oct-2011 MA 341 14 The Nagel Segment 1. -

(Almost) Equilateral Triangles
ON CEVA POINTS OF (ALMOST) EQUILATERAL TRIANGLES JEANNE LAFLAMME AND MATILDE LAL´IN Abstract. A Ceva point of a rational-sided triangle is any internal or external point such that the lengths of the three cevians through this point are rational. Buchholz [Buc89] studied Ceva points and showed a method to construct new Ceva points from a known one. We prove that almost-equilateral and equilateral rational triangles have infinitely many Ceva points by establishing a correspondence to points in certain elliptic surfaces of positive rank. 1. Introduction In 1801 Euler [Eul01] published an article presenting a parametrization of the triangles with the property that the distance from a vertex to the center of gravity is rational. Because this distance is two-thirds of the length of the median, this amounts to parametrizing the triangles whose medians have rational length. A Heron triangle is a triangle with rational sides and rational area. In 1981 Guy ([Guy04], Problem D21) posed the question of finding perfect triangles, namely, Heron triangles whose three medians are also rational. This particular problem remains open, with the main contribution being the parametrization of Heron triangles with two rational medians by Buchholz and Rathbun [BR97, BR98]. Further contributions to parametrizations of triangles with rational medians were made by Buchholz and various collaborators [Buc02, BBRS03, BS19], and by Ismail [Ism20]. Elliptic curves arising from such problems were studied by Dujella and Peral [DP13, DP14]. Heron triangles have been extensively studied by various authors, see for example [Sas99, KL00, GM06, Bre06, vL07, ILS07, SSSG+13, BS15, HH20]. In his PhD thesis [Buc89] Buchholz considered the more general situation of three cevians. -
![Arxiv:2101.02592V1 [Math.HO] 6 Jan 2021 in His Seminal Paper [10]](https://docslib.b-cdn.net/cover/7323/arxiv-2101-02592v1-math-ho-6-jan-2021-in-his-seminal-paper-10-957323.webp)
Arxiv:2101.02592V1 [Math.HO] 6 Jan 2021 in His Seminal Paper [10]
International Journal of Computer Discovered Mathematics (IJCDM) ISSN 2367-7775 ©IJCDM Volume 5, 2020, pp. 13{41 Received 6 August 2020. Published on-line 30 September 2020 web: http://www.journal-1.eu/ ©The Author(s) This article is published with open access1. Arrangement of Central Points on the Faces of a Tetrahedron Stanley Rabinowitz 545 Elm St Unit 1, Milford, New Hampshire 03055, USA e-mail: [email protected] web: http://www.StanleyRabinowitz.com/ Abstract. We systematically investigate properties of various triangle centers (such as orthocenter or incenter) located on the four faces of a tetrahedron. For each of six types of tetrahedra, we examine over 100 centers located on the four faces of the tetrahedron. Using a computer, we determine when any of 16 con- ditions occur (such as the four centers being coplanar). A typical result is: The lines from each vertex of a circumscriptible tetrahedron to the Gergonne points of the opposite face are concurrent. Keywords. triangle centers, tetrahedra, computer-discovered mathematics, Eu- clidean geometry. Mathematics Subject Classification (2020). 51M04, 51-08. 1. Introduction Over the centuries, many notable points have been found that are associated with an arbitrary triangle. Familiar examples include: the centroid, the circumcenter, the incenter, and the orthocenter. Of particular interest are those points that Clark Kimberling classifies as \triangle centers". He notes over 100 such points arXiv:2101.02592v1 [math.HO] 6 Jan 2021 in his seminal paper [10]. Given an arbitrary tetrahedron and a choice of triangle center (for example, the circumcenter), we may locate this triangle center in each face of the tetrahedron.