Interpolation and Curve Fitting
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Unsupervised Contour Representation and Estimation Using B-Splines and a Minimum Description Length Criterion Mário A
IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 9, NO. 6, JUNE 2000 1075 Unsupervised Contour Representation and Estimation Using B-Splines and a Minimum Description Length Criterion Mário A. T. Figueiredo, Member, IEEE, José M. N. Leitão, Member, IEEE, and Anil K. Jain, Fellow, IEEE Abstract—This paper describes a new approach to adaptive having external/potential energy, which is a func- estimation of parametric deformable contours based on B-spline tion of certain features of the image The equilibrium (min- representations. The problem is formulated in a statistical imal total energy) configuration framework with the likelihood function being derived from a re- gion-based image model. The parameters of the image model, the (1) contour parameters, and the B-spline parameterization order (i.e., the number of control points) are all considered unknown. The is a compromise between smoothness (enforced by the elastic parameterization order is estimated via a minimum description nature of the model) and proximity to the desired image features length (MDL) type criterion. A deterministic iterative algorithm is (by action of the external potential). developed to implement the derived contour estimation criterion. Several drawbacks of conventional snakes, such as their “my- The result is an unsupervised parametric deformable contour: it adapts its degree of smoothness/complexity (number of control opia” (i.e., use of image data strictly along the boundary), have points) and it also estimates the observation (image) model stimulated a great amount of research; although most limitations parameters. The experiments reported in the paper, performed of the original formulation have been successfully addressed on synthetic and real (medical) images, confirm the adequacy and (see, e.g., [6], [9], [10], [34], [38], [43], [49], and [52]), non- good performance of the approach. -
![Mathematical Construction of Interpolation and Extrapolation Function by Taylor Polynomials Arxiv:2002.11438V1 [Math.NA] 26 Fe](https://docslib.b-cdn.net/cover/2164/mathematical-construction-of-interpolation-and-extrapolation-function-by-taylor-polynomials-arxiv-2002-11438v1-math-na-26-fe-102164.webp)
Mathematical Construction of Interpolation and Extrapolation Function by Taylor Polynomials Arxiv:2002.11438V1 [Math.NA] 26 Fe
Mathematical Construction of Interpolation and Extrapolation Function by Taylor Polynomials Nijat Shukurov Department of Engineering Physics, Ankara University, Ankara, Turkey E-mail: [email protected] , [email protected] Abstract: In this present paper, I propose a derivation of unified interpolation and extrapolation function that predicts new values inside and outside the given range by expanding direct Taylor series on the middle point of given data set. Mathemati- cal construction of experimental model derived in general form. Trigonometric and Power functions adopted as test functions in the development of the vital aspects in numerical experiments. Experimental model was interpolated and extrapolated on data set that generated by test functions. The results of the numerical experiments which predicted by derived model compared with analytical values. KEYWORDS: Polynomial Interpolation, Extrapolation, Taylor Series, Expansion arXiv:2002.11438v1 [math.NA] 26 Feb 2020 1 1 Introduction In scientific experiments or engineering applications, collected data are usually discrete in most cases and physical meaning is likely unpredictable. To estimate the outcomes and to understand the phenomena analytically controllable functions are desirable. In the mathematical field of nu- merical analysis those type of functions are called as interpolation and extrapolation functions. Interpolation serves as the prediction tool within range of given discrete set, unlike interpola- tion, extrapolation functions designed to predict values out of the range of given data set. In this scientific paper, direct Taylor expansion is suggested as a instrument which estimates or approximates a new points inside and outside the range by known individual values. Taylor se- ries is one of most beautiful analogies in mathematics, which make it possible to rewrite every smooth function as a infinite series of Taylor polynomials. -

On Multivariate Interpolation
On Multivariate Interpolation Peter J. Olver† School of Mathematics University of Minnesota Minneapolis, MN 55455 U.S.A. [email protected] http://www.math.umn.edu/∼olver Abstract. A new approach to interpolation theory for functions of several variables is proposed. We develop a multivariate divided difference calculus based on the theory of non-commutative quasi-determinants. In addition, intriguing explicit formulae that connect the classical finite difference interpolation coefficients for univariate curves with multivariate interpolation coefficients for higher dimensional submanifolds are established. † Supported in part by NSF Grant DMS 11–08894. April 6, 2016 1 1. Introduction. Interpolation theory for functions of a single variable has a long and distinguished his- tory, dating back to Newton’s fundamental interpolation formula and the classical calculus of finite differences, [7, 47, 58, 64]. Standard numerical approximations to derivatives and many numerical integration methods for differential equations are based on the finite dif- ference calculus. However, historically, no comparable calculus was developed for functions of more than one variable. If one looks up multivariate interpolation in the classical books, one is essentially restricted to rectangular, or, slightly more generally, separable grids, over which the formulae are a simple adaptation of the univariate divided difference calculus. See [19] for historical details. Starting with G. Birkhoff, [2] (who was, coincidentally, my thesis advisor), recent years have seen a renewed level of interest in multivariate interpolation among both pure and applied researchers; see [18] for a fairly recent survey containing an extensive bibli- ography. De Boor and Ron, [8, 12, 13], and Sauer and Xu, [61, 10, 65], have systemati- cally studied the polynomial case. -

Easy Way to Find Multivariate Interpolation
IJETST- Vol.||04||Issue||05||Pages 5189-5193||May||ISSN 2348-9480 2017 International Journal of Emerging Trends in Science and Technology IC Value: 76.89 (Index Copernicus) Impact Factor: 4.219 DOI: https://dx.doi.org/10.18535/ijetst/v4i5.11 Easy way to Find Multivariate Interpolation Author Yimesgen Mehari Faculty of Natural and Computational Science, Department of Mathematics Adigrat University, Ethiopia Email: [email protected] Abstract We derive explicit interpolation formula using non-singular vandermonde matrix for constructing multi dimensional function which interpolates at a set of distinct abscissas. We also provide examples to show how the formula is used in practices. Introduction Engineers and scientists commonly assume that past and currently. But there is no theoretical relationships between variables in physical difficulty in setting up a frame work for problem can be approximately reproduced from discussing interpolation of multivariate function f data given by the problem. The ultimate goal whose values are known.[1] might be to determine the values at intermediate Interpolation function of more than one variable points, to approximate the integral or to simply has become increasingly important in the past few give a smooth or continuous representation of the years. These days, application ranges over many variables in the problem different field of pure and applied mathematics. Interpolation is the method of estimating unknown For example interpolation finds applications in the values with the help of given set of observations. numerical integrations of differential equations, According to Theile Interpolation is, “The art of topography, and the computer aided geometric reading between the lines of the table” and design of cars, ships, airplanes.[1] According to W.M. -

Chapter 26: Mathcad-Data Analysis Functions
Lecture 3 MATHCAD-DATA ANALYSIS FUNCTIONS Objectives Graphs in MathCAD Built-in Functions for basic calculations: Square roots, Systems of linear equations Interpolation on data sets Linear regression Symbolic calculation Graphing with MathCAD Plotting vector against vector: The vectors must have equal number of elements. MathCAD plots values in its default units. To change units in the plot……? Divide your axis by the desired unit. Or remove the units from the defined vectors Use Graph Toolbox or [Shift-2] Or Insert/Graph from menu Graphing 1 20 2 28 time 3 min Temp 35 K time 4 42 Time min 5 49 40 40 Temp Temp 20 20 100 200 300 2 4 time Time Graphing with MathCAD 1 20 Plotting element by 2 28 element: define a time 3 min Temp 35 K 4 42 range variable 5 49 containing as many i 04 element as each of the vectors. 40 i:=0..4 Temp i 20 100 200 300 timei QuickPlots Use when you want to x 0 0.12 see what a function looks like 1 Create a x-y graph Enter the function on sin(x) 0 y-axis with parameter(s) 1 Enter the parameter on 0 2 4 6 x-axis x Graphing with MathCAD Plotting multiple curves:up to 16 curves in a single graph. Example: For 2 dependent variables (y) and 1 independent variable (x) Press shift2 (create a x-y plot) On the y axis enter the first y variable then press comma to enter the second y variable. On the x axis enter your x variable. -

Spatial Interpolation Methods
Page | 0 of 0 SPATIAL INTERPOLATION METHODS 2018 Page | 1 of 1 1. Introduction Spatial interpolation is the procedure to predict the value of attributes at unobserved points within a study region using existing observations (Waters, 1989). Lam (1983) definition of spatial interpolation is “given a set of spatial data either in the form of discrete points or for subareas, find the function that will best represent the whole surface and that will predict values at points or for other subareas”. Predicting the values of a variable at points outside the region covered by existing observations is called extrapolation (Burrough and McDonnell, 1998). All spatial interpolation methods can be used to generate an extrapolation (Li and Heap 2008). Spatial Interpolation is the process of using points with known values to estimate values at other points. Through Spatial Interpolation, We can estimate the precipitation value at a location with no recorded data by using known precipitation readings at nearby weather stations. Rationale behind spatial interpolation is the observation that points close together in space are more likely to have similar values than points far apart (Tobler’s Law of Geography). Spatial Interpolation covers a variety of method including trend surface models, thiessen polygons, kernel density estimation, inverse distance weighted, splines, and Kriging. Spatial Interpolation requires two basic inputs: · Sample Points · Spatial Interpolation Method Sample Points Sample Points are points with known values. Sample points provide the data necessary for the development of interpolator for spatial interpolation. The number and distribution of sample points can greatly influence the accuracy of spatial interpolation. -

Comparison of Gap Interpolation Methodologies for Water Level Time Series Using Perl/Pdl
Revista de Matematica:´ Teor´ıa y Aplicaciones 2005 12(1 & 2) : 157–164 cimpa – ucr – ccss issn: 1409-2433 comparison of gap interpolation methodologies for water level time series using perl/pdl Aimee Mostella∗ Alexey Sadovksi† Scott Duff‡ Patrick Michaud§ Philippe Tissot¶ Carl Steidleyk Received/Recibido: 13 Feb 2004 Abstract Extensive time series of measurements are often essential to evaluate long term changes and averages such as tidal datums and sea level rises. As such, gaps in time series data restrict the type and extent of modeling and research which may be accomplished. The Texas A&M University Corpus Christi Division of Nearshore Research (TAMUCC-DNR) has developed and compared various methods based on forward and backward linear regression to interpolate gaps in time series of water level data. We have developed a software system that retrieves actual and harmonic water level data based upon user provided parameters. The actual water level data is searched for missing data points and the location of these gaps are recorded. Forward and backward linear regression are applied in relation to the location of missing data or gaps in the remaining data. After this process is complete, one of three combinations of the forward and backward regression is used to fit the results. Finally, the harmonic component is added back into the newly supplemented time series and the results are graphed. The software created to implement this process of linear regression is written in Perl along with a Perl module called PDL (Perl Data Language). Generally, this process has demonstrated excellent results in filling gaps in our water level time series. -
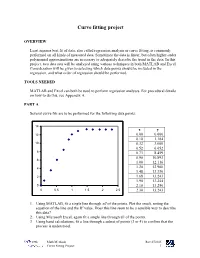
Curve Fitting Project
Curve fitting project OVERVIEW Least squares best fit of data, also called regression analysis or curve fitting, is commonly performed on all kinds of measured data. Sometimes the data is linear, but often higher-order polynomial approximations are necessary to adequately describe the trend in the data. In this project, two data sets will be analyzed using various techniques in both MATLAB and Excel. Consideration will be given to selecting which data points should be included in the regression, and what order of regression should be performed. TOOLS NEEDED MATLAB and Excel can both be used to perform regression analyses. For procedural details on how to do this, see Appendix A. PART A Several curve fits are to be performed for the following data points: 14 x y 12 0.00 0.000 0.10 1.184 10 0.32 3.600 0.52 6.052 8 0.73 8.459 0.90 10.893 6 1.00 12.116 4 1.20 12.900 1.48 13.330 2 1.68 13.243 1.90 13.244 0 2.10 13.250 0 0.5 1 1.5 2 2.5 2.30 13.243 1. Using MATLAB, fit a single line through all of the points. Plot the result, noting the equation of the line and the R2 value. Does this line seem to be a sensible way to describe this data? 2. Using Microsoft Excel, again fit a single line through all of the points. 3. Using hand calculations, fit a line through a subset of points (3 or 4) to confirm that the process is understood. -
Nonlinear Least-Squares Curve Fitting with Microsoft Excel Solver
Information • Textbooks • Media • Resources edited by Computer Bulletin Board Steven D. Gammon University of Idaho Moscow, ID 83844 Nonlinear Least-Squares Curve Fitting with Microsoft Excel Solver Daniel C. Harris Chemistry & Materials Branch, Research & Technology Division, Naval Air Warfare Center,China Lake, CA 93555 A powerful tool that is widely available in spreadsheets Unweighted Least Squares provides a simple means of fitting experimental data to non- linear functions. The procedure is so easy to use and its Experimental values of x and y from Figure 1 are listed mode of operation is so obvious that it is an excellent way in the first two columns of the spreadsheet in Figure 2. The for students to learn the underlying principle of least- vertical deviation of the ith point from the smooth curve is squares curve fitting. The purpose of this article is to intro- vertical deviation = yi (observed) – yi (calculated) (2) duce the method of Walsh and Diamond (1) to readers of = yi – (Axi + B/xi + C) this Journal, to extend their treatment to weighted least The least squares criterion is to find values of A, B, and squares, and to add a simple method for estimating uncer- C in eq 1 that minimize the sum of the squares of the verti- tainties in the least-square parameters. Other recipes for cal deviations of the points from the curve: curve fitting have been presented in numerous previous papers (2–16). n 2 Σ Consider the problem of fitting the experimental gas sum = yi ± Axi + B / xi + C (3) chromatography data (17) in Figure 1 with the van Deemter i =1 equation: where n is the total number of points (= 13 in Fig. -

Bayesian Interpolation of Unequally Spaced Time Series
Bayesian interpolation of unequally spaced time series Luis E. Nieto-Barajas and Tapen Sinha Department of Statistics and Department of Actuarial Sciences, ITAM, Mexico [email protected] and [email protected] Abstract A comparative analysis of time series is not feasible if the observation times are different. Not even a simple dispersion diagram is possible. In this article we propose a Gaussian process model to interpolate an unequally spaced time series and produce predictions for equally spaced observation times. The dependence between two obser- vations is assumed a function of the time differences. The novelty of the proposal relies on parametrizing the correlation function in terms of Weibull and Log-logistic survival functions. We further allow the correlation to be positive or negative. Inference on the model is made under a Bayesian approach and interpolation is done via the posterior predictive conditional distributions given the closest m observed times. Performance of the model is illustrated via a simulation study as well as with real data sets of temperature and CO2 observed over 800,000 years before the present. Key words: Bayesian inference, EPICA, Gaussian process, kriging, survival functions. 1 Introduction The majority of the literature on time series analysis assumes that the variable of interest, say Xt, is observed on a regular or equally spaced sequence of times, say t 2 f1; 2;:::g (e.g. Box et al. 2004; Chatfield 1989). Often, time series are observed at uneven times. Unequally spaced (also called unevenly or irregularly spaced) time series data occur naturally in many fields. For instance, natural disasters, such as earthquakes, floods and volcanic eruptions, occur at uneven intervals. -

Multivariate Lagrange Interpolation 1 Introduction 2 Polynomial
Alex Lewis Final Project Multivariate Lagrange Interpolation Abstract. Explain how the standard linear Lagrange interpolation can be generalized to construct a formula that interpolates a set of points in . We will also provide examples to show how the formula is used in practice. 1 Introduction Interpolation is a fundamental topic in Numerical Analysis. It is the practice of creating a function that fits a finite sampled data set. These sampled values can be used to construct an interpolant, which must fit the interpolated function at each date point. 2 Polynomial Interpolation “The Problem of determining a polynomial of degree one that passes through the distinct points and is the same as approximating a function for which and by means of a first degree polynomial interpolating, or agreeing with, the values of f at the given points. We define the functions and , And then define We can generalize this concept of linear interpolation and consider a polynomial of degree n that passes through n+1 points. In this case we can construct, for each , a function with the property that when and . To satisfy for each requires that the numerator of contains the term To satisfy , the denominator of must be equal to this term evaluated at . Thus, This is called the Th Lagrange Interpolating Polynomial The polynomial is given once again as, Example 1 If and , then is the polynomial that agrees with at , and ; that is, 3 Multivariate Interpolation First we define a function be an -variable multinomial function of degree . In other words, the , could, in our case be ; in this case it would be a 3 variable function of some degree . -

(EU FP7 2013 - 612218/3D-NET) 3DNET Sops HOW-TO-DO PRACTICAL GUIDE
3D-NET (EU FP7 2013 - 612218/3D-NET) 3DNET SOPs HOW-TO-DO PRACTICAL GUIDE Curve fitting This is intended to be an aid-memoir for those involved in fitting biological data to dose response curves in why we do it and how to best do it. So why do we use non linear regression? Much of the data generated in Biology is sigmoidal dose response (E/[A]) curves, the aim is to generate estimates of upper and lower asymptotes, A50 and slope parameters and their associated confidence limits. How can we analyse E/[A] data? Why fit curves? What’s wrong with joining the dots? Fitting Uses all the data points to estimate each parameter Tell us the confidence that we can have in each parameter estimate Estimates a slope parameter Fitting curves to data is model fitting. The general equation for a sigmoidal dose-response curve is commonly referred to as the ‘Hill equation’ or the ‘four-parameter logistic equation”. (Top Bottom) Re sponse Bottom EC50hillslope 1 [Drug]hillslpoe The models most commonly used in Biology for fitting these data are ‘model 205 – Dose response one site -4 Parameter Logistic Model or Sigmoidal Dose-Response Model’ in XLfit (package used in ActivityBase or Excel) and ‘non-linear regression - sigmoidal variable slope’ in GraphPad Prism. What the computer does - Non-linear least squares Starts with an initial estimated value for each variable in the equation Generates the curve defined by these values Calculates the sum of squares Adjusts the variables to make the curve come closer to the data points (Marquardt method) Re-calculates the sum of squares Continues this iteration until there’s virtually no difference between successive fittings.