DOCSLIB.ORG

Estimating the Number of Unseen Variants in the Human Genome

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Estimating the Number of Unseen Variants in the Human Genome Estimating the number of unseen variants in the human genome Iuliana Ionita-Laza1, Christoph Lange, and Nan M. Laird Department of Biostatistics, Harvard School of Public Health, 655 Huntington Avenue, Boston, MA 02115b; Edited by Peter J. Bickel, University of California, Berkeley, CA, and approved January 7, 2009 (received for review August 8, 2008) The different genetic variation discovery projects (The SNP Consor- not use. Specifically, if a new volume by Shakespeare were to be tium, the International HapMap Project, the 1000 Genomes Project, discovered, how many new words would we expect to see? Efron etc.) aim to identify as much as possible of the underlying genetic and Thisted (7) used a Gamma-Poisson model to address this variation in various human populations. The question we address in question. We adapt the approach in Efron and Thisted to the this article is how many new variants are yet to be found. This is an problem of predicting the number of genetic variants yet to be instance of the species problem in ecology, where the goal is to esti- identified in future studies. The method also allows calculation of mate the number of species in a closed population. We use a para- the number of individuals required to be sequenced in order to metric beta-binomial model that allows us to calculate the expected detect all (or a fraction of) the variants with a given minimum fre- number of new variants with a desired minimum frequency to be quency. In the following sections we develop the method and show discovered in a new dataset of individuals of a specified size. The applications to several available sequence datasets: ENCODE, method can also be used to predict the number of individuals nec- SeattleSNPs, and National Institute on Environmental Health Sci- essary to sequence in order to capture all (or a fraction of) the vari- ences (NIEHS) SNPs. Although these datasets contain only SNPs, ation with a specified minimum frequency. We apply the method the method can be applied to counting other types of variants, to three datasets: the ENCODE dataset, the SeattleSNPs dataset, including copy-number variants. and the National Institute of Environmental Health Sciences SNPs dataset. Consistent with previous descriptions, our results show 1. Methods that the African population is the most diverse in terms of the number of variants expected to exist, the Asian populations the First, we introduce some notation. For our purposes, an individ- least diverse, with the European population in-between. In addi- ual shows variation at a particular position if the correspond- tion, our results show a clear distinction between the Chinese and ing allele is different from the ancestral allele. We say that a the Japanese populations, with the Japanese population being the position is variable (or is a variant) in a sample if there is at less diverse. To find all common variants (frequency at least 1%) the least one individual in the sample that shows variation at that number of individuals that need to be sequenced is small (∼350) position. N and does not differ much among the different populations; our Suppose we have data on ind individuals; for example, each N data show that, subject to sequence accuracy, the 1000 Genomes of the ind individuals has been sequenced in a genomic region, Project is likely to find most of these common variants and a high and hence for each position we know whether an individual shows proportion of the rarer ones (frequency between 0.1 and 1%). The variation or not. data reveal a rule of diminishing returns: a small number of individ- We follow the notation in ref. 7. Suppose the total number of uals (∼150) is sufficient to identify 80% of variants with a frequency variable positions in the human genome is an unknown, fixed num- N f of at least 0.1%, while a much larger number (>3,000 individuals) is ber, denoted here by .Let s be the unobserved frequency of s x necessary to find all of those variants. Finally, our results also show variable position , and let s be the number of times variable s N a much higher diversity in environmental response genes compared position has been observed in the ind individuals in our dataset. x ∼ N f with the average genome, especially in African populations. Then, s Bin( ind, s). Of course, we can only observe those variable positions with xs > 0. We assume that fs ∼ Beta(a, b). The Beta prior is not only mathematically convenient, but a good 1000 Genomes Project | beta-binomial model | CNVs | sequence data | SNP approximation for the distribution of allele frequencies at biallelic markers under a neutral selection and mutation-drift equilibrium main goal of the various human genome projects is to dis- model, as Wright (8) showed. A cover genetic variants in human genomes. The HapMap Let nx be the number of positions with exactly x individuals project (http://www.hapmap.org/) has contributed much to our showing variation at a position. Hence, n1 is the number of vari- understanding of the underlying genetic variation in diverse Nind ants that occur in only one individual, etc., and = nx is the total human populations and has facilitated the discovery of many loci x 1 number of variants observed. Also, let ηx = E(nx). robustly associated with common human diseases, such as dia- As in ref. 7, we want to estimate (t), i.e., the number of new betes, obesity, breast cancer, and many others (1–5). The recently variants to be found in the next t · Nind individuals (if we were to launched 1000 Genomes Project (http://www.1000genomes.org/), perform a new sequencing study of that size). For t ≥ 0, we can by sequencing 1,000 genomes, aims to discover much of the exis- write tent common variation (frequency at least 1%), including both single-nucleotide polymorphisms (SNPs) and the less explored copy-number variants (6). In this article, we provide a systematic way to predict the number Author contributions: I.I.-L. and N.M.L. designed research; I.I.-L. and N.M.L. performed of new variants with a specified minimum frequency to be iden- research; I.I.-L. and C.L. contributed new reagents/analytic tools; I.I.-L., C.L., and N.M.L. tified in future datasets of specified sizes. In particular, based on analyzed data; and I.I.-L. and N.M.L. wrote the paper. sequence data for a set of individuals, can we predict how many The authors declare no conflict of interest. more new variants will be found if we were to sequence a new This article is a PNAS Direct Submission. set of individuals of a given size? This question is related to the 1To whom correspondence should be addressed. E-mail: [email protected]. species problem in ecology, where one is interested in estimating This article contains supporting information online at www.pnas.org/cgi/content/full/ the number of species in a closed population. A particular exam- 0807815106/DCSupplemental. ple is estimating the number of words Shakespeare knew but did © 2009 by The National Academy of Sciences of the USA 5008–5013 PNAS March 31, 2009 vol. 106 no. 13 www.pnas.org / cgi / doi / 10.1073 / pnas.0807815106 Downloaded by guest on September 26, 2021 1 + · (t) = N 1 − (1 − θ)(t 1) Nind f (θ)dθ 1.1. Estimation of the Parameters a and b of the Beta Distribution. To a b 0 estimate and , we use maximum-likelihood estimation. The 1 probability that exactly x individuals show variation at a position is: − N 1 − (1 − θ)Nind f (θ)dθ 1 0 Nind − x Nind x 1 1 Px = θ (1 − θ) f (θ)dθ + · x = N (1 − θ)Nind f (θ)dθ − N (1 − θ)(t 1) Nind f (θ)dθ 0 1 x+a−1 N −x+b−1 0 0 Nind θ (1 − θ) ind [1] = dθ x B(a, b) 0 Nind B(x + a, Nind − x + b) where f (θ) = θ a−1 · (1 − θ)b−1/B(a, b) is the density function for = x B(a, b) = 1 a−1 − b−1 the Beta distribution and B(a, b) 0 θ (1 θ) dθ is the beta function. for x ≥ 0. As we already mentioned, the zero class is not observed Inserting the form for f (θ) into Eq. 1 we obtain: and hence we need to fit the zero-truncated beta-binomial dis- tribution. The probability distribution function for this truncated distribution becomes: 1 N − + − = a 1 − Nind b 1 (t) θ (1 θ) dθ t = Px B(a, b) 0 Px Nind 1 x=1 Px N − + · + − − a 1 − (t 1) Nind b 1 θ (1 θ) dθ for x ≥ 1. The likelihood function can then be written as: B(a, b) 0 + − N = η1 · Nind b 1 ind = t nx a Nind L(a, b) Px + − + · + x=1 − η1 · Nind b 1 · B(a,(t 1) Nind b) a Nind B(a, Nind + b) and the log-likelihood function is: N ind Detailed derivations are shown in the supporting information LL(a, b) = n log Pt (SI) Appendix. Note that (0) = 0 and x x x=1 η N + b − 1 We maximize LL(a, b) to obtain the maximum-likelihood esti- (t) → 1 · ind mators (MLEs) for a and b. The maximization is carried out a Nind through the Newton–Raphson method. Note that in the likelihood function above, we assume that when t →∞. markers are in linkage equilibrium. Dependence among nearby In addition, we can calculate f (t), i.e., the number of new vari- markers makes the effective number of markers in the region look ants with frequency at least f expected to be found in a new set of smaller, but does not lead to systematic bias.
Load more

Recommended publications
  • ENCODE Regions Identification of Higher-Order Functional Domains in the Human
    Downloaded from www.genome.org on August 14, 2007 Identification of higher-order functional domains in the human ENCODE regions Robert E. Thurman, Nathan Day, William S. Noble and John A. Stamatoyannopoulos Genome Res. 2007 17: 917-927 Access the most recent version at doi:10.1101/gr.6081407 Supplementary "Supplemental Research Data" data http://www.genome.org/cgi/content/full/17/6/917/DC1 References This article cites 45 articles, 17 of which can be accessed free at: http://www.genome.org/cgi/content/full/17/6/917#References Article cited in: http://www.genome.org/cgi/content/full/17/6/917#otherarticles Open Access Freely available online through the Genome Research Open Access option. Email alerting Receive free email alerts when new articles cite this article - sign up in the box at the service top right corner of the article or click here Notes To subscribe to Genome Research go to: http://www.genome.org/subscriptions/ © 2007 Cold Spring Harbor Laboratory Press Downloaded from www.genome.org on August 14, 2007 Methods Identification of higher-order functional domains in the human ENCODE regions Robert E. Thurman,1,2 Nathan Day,3 William S. Noble,2,3 and John A. Stamatoyannopoulos2,4 1Division of Medical Genetics, University of Washington, Seattle, Washington 98195, USA; 2Department of Genome Sciences, University of Washington, Seattle, Washington 98195, USA; 3Department of Computer Science and Engineering, University of Washington, Seattle, Washington 98195, USA It has long been posited that human and other large genomes are organized into higher-order (i.e., greater than gene-sized) functional domains.
    [Show full text]
  • Developing and Implementing an Institute-Wide Data Sharing Policy Stephanie OM Dyke and Tim JP Hubbard*
    Dyke and Hubbard Genome Medicine 2011, 3:60 http://genomemedicine.com/content/3/9/60 CORRESPONDENCE Developing and implementing an institute-wide data sharing policy Stephanie OM Dyke and Tim JP Hubbard* Abstract HapMap Project [7], also decided to follow HGP prac- tices and to share data publicly as a resource for the The Wellcome Trust Sanger Institute has a strong research community before academic publications des- reputation for prepublication data sharing as a result crib ing analyses of the data sets had been prepared of its policy of rapid release of genome sequence (referred to as prepublication data sharing). data and particularly through its contribution to the Following the success of the first phase of the HGP [8] Human Genome Project. The practicalities of broad and of these other projects, the principles of rapid data data sharing remain largely uncharted, especially to release were reaffirmed and endorsed more widely at a cover the wide range of data types currently produced meeting of genomics funders, scientists, public archives by genomic studies and to adequately address and publishers in Fort Lauderdale in 2003 [9]. Meanwhile, ethical issues. This paper describes the processes the Organisation for Economic Co-operation and and challenges involved in implementing a data Develop ment (OECD) Committee on Scientific and sharing policy on an institute-wide scale. This includes Tech nology Policy had established a working group on questions of governance, practical aspects of applying issues of access to research information [10,11], which principles to diverse experimental contexts, building led to a Declaration on access to research data from enabling systems and infrastructure, incentives and public funding [12], and later to a set of OECD guidelines collaborative issues.
    [Show full text]
  • The ENCODE Project
    RESEARCH HIGHLIGHTS GENOMICS The ENCODE project The second, genome-wide phase of a particular product (for instance, a protein ENCODE-defined functional element in at the Encyclopedia of DNA Elements or noncoding RNA) or has a consistent bio- least one examined cell type; an even larger (ENCODE) project is being reported. chemical property (for instance, being bound fraction (99%) lies nearby such an element The function of most of the human by protein or having a particular biochemical (within 1.7 kilobases). An examination of genome is unknown. Protein-coding genes mark). previously identified disease-associated account for only a small fraction (about 3%) The laboratories in the ENCODE Project single-nucleotide polymorphisms shows that of the total genome sequence; most func- Consortium have developed and applied a they are enriched in ENCODE-annotated tional genomic sequences are likely to have huge range of sequencing-based techniques regions, suggesting hypotheses for functional regulatory roles. Understanding human to map functional elements across the consequences of single-nucleotide polymor- gene organization and regulation and their genome. To put it succinctly, the ENCODE phisms that can be further tested. impact on normal and disease phenotypes project has mapped chromatin state and The data generated by ENCODE are vast requires that functional elements be mapped structure, three-dimensional genome organi- and can be only very briefly summarized and annotated across the genome. This is the zation, DNA methylation, transcription fac- here. The collected ENCODE papers may goal of the ENCODE project. tor binding, RNA transcription and protein be examined at http://www.encodeproject. The initial 5-year pilot phase of the proj- expression genome wide.
    [Show full text]
  • The ENCODE (Encyclopedia of S DNA Elements) Project
    GGENESENES IN INAACTIONCTION VIEWPOINT ECTION The ENCODE (ENCyclopedia Of S DNA Elements) Project PECIAL The ENCODE Project Consortium*. S The ENCyclopedia Of DNA Elements (ENCODE) Project aims to identify all functional approaches, such as cDNA-cloning efforts elements in the human genome sequence. The pilot phase of the Project is focused on (4, 5) and chip-based transcriptome analyses a specified 30 megabases (È1%) of the human genome sequence and is organized as (6, 7), have revealed the existence of many an international consortium of computational and laboratory-based scientists transcribed sequences of unknown function. working to develop and apply high-throughput approaches for detecting all sequence As a reflection of this complexity, about 5% elements that confer biological function. The results of this pilot phase will guide of the human genome is evolutionarily future efforts to analyze the entire human genome. conserved with respect to rodent genomic sequences, and therefore is inferred to be With the complete human genome sequence namics; undoubtedly, additional, yet-to-be- functionally important (8, 9). Yet only about now in hand (1–3), we face the enormous defined types of functional sequences will one-third of the sequence under such selec- challenge of interpreting it and learning how also need to be included. tion is predicted to encode proteins (1, 2). to use that information to understand the To illustrate the magnitude of the chal- Our collective knowledge about putative biology of human health and disease. The lenge involved, it only needs to be pointed out functional, noncoding elements, which repre- ENCyclopedia Of DNA Elements (ENCODE) that an inventory of the best-defined func- sent the majority of the remaining functional Project is predicated on the belief that a tional components in the human genome— sequences in the human genome, is remark- comprehensive catalog of the structural and the protein-coding sequences—is still incom- ably underdeveloped at the present time.
    [Show full text]
  • What Is a Gene, Post-ENCODE? History and Updated Definition
    Downloaded from genome.cshlp.org on October 2, 2021 - Published by Cold Spring Harbor Laboratory Press Perspective What is a gene, post-ENCODE? History and updated definition Mark B. Gerstein,1,2,3,9 Can Bruce,2,4 Joel S. Rozowsky,2 Deyou Zheng,2 Jiang Du,3 Jan O. Korbel,2,5 Olof Emanuelsson,6 Zhengdong D. Zhang,2 Sherman Weissman,7 and Michael Snyder2,8 1Program in Computational Biology & Bioinformatics, Yale University, New Haven, Connecticut 06511, USA; 2Molecular Biophysics & Biochemistry Department, Yale University, New Haven, Connecticut 06511, USA; 3Computer Science Department, Yale University, New Haven, Connecticut 06511, USA; 4Center for Medical Informatics, Yale University, New Haven, Connecticut 06511, USA; 5European Molecular Biology Laboratory, 69117 Heidelberg, Germany; 6Stockholm Bioinformatics Center, Albanova University Center, Stockholm University, SE-10691 Stockholm, Sweden; 7Genetics Department, Yale University, New Haven, Connecticut 06511, USA; 8Molecular, Cellular, & Developmental Biology Department, Yale University, New Haven, Connecticut 06511, USA While sequencing of the human genome surprised us with how many protein-coding genes there are, it did not fundamentally change our perspective on what a gene is. In contrast, the complex patterns of dispersed regulation and pervasive transcription uncovered by the ENCODE project, together with non-genic conservation and the abundance of noncoding RNA genes, have challenged the notion of the gene. To illustrate this, we review the evolution of operational definitions of a gene over the past century—from the abstract elements of heredity of Mendel and Morgan to the present-day ORFs enumerated in the sequence databanks. We then summarize the current ENCODE findings and provide a computational metaphor for the complexity.
    [Show full text]
  • A User's Guide to the Encyclopedia of DNA Elements (ENCODE)
    A User’s Guide to the Encyclopedia of DNA Elements (ENCODE) The ENCODE Project Consortium"* Abstract The mission of the Encyclopedia of DNA Elements (ENCODE) Project is to enable the scientific and medical communities to interpret the human genome sequence and apply it to understand human biology and improve health. The ENCODE Consortium is integrating multiple technologies and approaches in a collective effort to discover and define the functional elements encoded in the human genome, including genes, transcripts, and transcriptional regulatory regions, together with their attendant chromatin states and DNA methylation patterns. In the process, standards to ensure high-quality data have been implemented, and novel algorithms have been developed to facilitate analysis. Data and derived results are made available through a freely accessible database. Here we provide an overview of the project and the resources it is generating and illustrate the application of ENCODE data to interpret the human genome. Citation: The ENCODE Project Consortium (2011) A User’s Guide to the Encyclopedia of DNA Elements (ENCODE). PLoS Biol 9(4): e1001046. doi:10.1371/ journal.pbio.1001046 Academic Editor: Peter B. Becker, Adolf Butenandt Institute, Germany Received September 23, 2010; Accepted March 10, 2011; Published April 19, 2011 Copyright: ß 2011 The ENCODE Project Consortium. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. Funding: Funded by the National Human Genome Research Institute, National Institutes of Health, Bethesda, MD, USA. The role of the NIH Project Management Group in the preparation of this paper was limited to coordination and scientific management of the ENCODE Consortium.
    [Show full text]
  • Current Advances of Epigenetics in Periodontology from ENCODE Project
    Cho et al. Clin Epigenet (2021) 13:92 https://doi.org/10.1186/s13148-021-01074-w REVIEW Open Access Current advances of epigenetics in periodontology from ENCODE project: a review and future perspectives Young‑Dan Cho1, Woo‑Jin Kim2, Hyun‑Mo Ryoo2, Hong‑Gee Kim3, Kyoung‑Hwa Kim1, Young Ku1 and Yang‑Jo Seol1* Abstract Background: The Encyclopedia of DNA Elements (ENCODE) project has advanced our knowledge of the functional elements in the genome and epigenome. The aim of this article was to provide the comprehension about current research trends from ENCODE project and establish the link between epigenetics and periodontal diseases based on epigenome studies and seek the future direction. Main body: Global epigenome research projects have emphasized the importance of epigenetic research for under‑ standing human health and disease, and current international consortia show an improved interest in the importance of oral health with systemic health. The epigenetic studies in dental feld have been mainly conducted in periodontol‑ ogy and have focused on DNA methylation analysis. Advances in sequencing technology have broadened the target for epigenetic studies from specifc genes to genome‑wide analyses. Conclusions: In line with global research trends, further extended and advanced epigenetic studies would provide crucial information for the realization of comprehensive dental medicine and expand the scope of ongoing large‑ scale research projects. Keywords: Chronic disease, Epigenetics, ENCODE project, Next‑generation sequencing, Periodontology, Personalized medicine Background research projects, such as the NIH Roadmap Epigenome Te Encyclopedia of DNA Elements (ENCODE) project Program and International Human Epigenome Consor- has advanced our knowledge of the functional elements tium, emphasized the importance of epigenetic research in the genome and epigenome, including chromatin for understanding human health and disease [2].
    [Show full text]
  • DNA Copy Number Analysis of Fresh and Formalin-Fixed Specimens By
    Downloaded from genome.cshlp.org on October 6, 2021 - Published by Cold Spring Harbor Laboratory Press DNA copy number analysis of fresh and formalin-fixed specimens by shallow whole-genome sequencing with identification and exclusion of problematic regions in the genome assembly Ilari Scheinin1;2;∗ Daoud Sie1;∗ Henrik Bengtsson3;4 Mark A. van de Wiel5;6 Adam B. Olshen3;4 Hinke F. van Thuijl1;7 Hendrik F. van Essen1 Paul P. Eijk1 Fran¸coisRustenburg1 Gerrit A. Meijer1 Jaap C. Reijneveld7;8 Pieter Wesseling1;9 Daniel Pinkel3;10 Donna G. Albertson3;10;11 Bauke Ylstra1 September 11, 2014 1. Department of Pathology, VU University Medical Center, Amsterdam, The Netherlands 2. Department of Pathology, Haartman Institute and HUSLAB, University of Helsinki and Helsinki University Central Hospital, Finland 3. Helen Diller Family Comprehensive Cancer Center, University of California San Francisco, San Francisco, California, USA 4. Department of Epidemiology and Biostatistics, University of California San Francisco, San Francisco, California, USA 5. Department of Epidemiology and Biostatistics, VU University Medical Center, Amsterdam, The Netherlands 6. Department of Mathematics, VU University, Amsterdam, The Netherlands 7. Department of Neurology, VU University Medical Center, Amsterdam, The Netherlands 8. Department of Neurology, Academic Medical Centre, Amsterdam, The Netherlands 9. Department of Pathology, Radboud University Medical Centre, Nijmegen, The Netherlands 10. Department of Laboratory Medicine, University of California San Francisco,
    [Show full text]
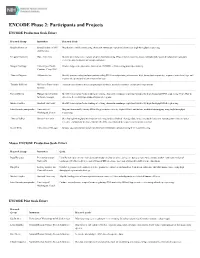
  • ENCODE Phase 2: Participants and Projects
    ENCODE Phase 2: Participants and Projects ENCODE Production Scale Effort Research Group Institution Research Goals Bradley Bernstein Broad Institute of MIT Map histone modifications using chromatin immunoprecipitation followed by high-throughput sequencing. and Harvard Gregory Crawford Duke University Identify and characterize regions of open chromatin using DNaseI hypersensitivity assays, formaldehyde-assisted isolation of regulatory elements, and chromatin immunoprecipitation. Morgan Giddings University of North Produce large-scale proteomic data sets on ENCODE cell lines using mass spectrometry. Carolina, Chapel Hill Thomas Gingeras Affymetrix, Inc. Identify protein-coding and non-protein coding RNA transcripts using microarrays, high-throughput sequencing, sequence paired-end tags, and sequenced cap analysis of gene expression tags. Timothy Hubbard Wellcome Trust Sanger Annotate gene features using computational methods, manual annotation, and targeted experiments. Institute Richard Myers HudsonAlpha Institute Identify transcription factor binding sites using chromatin immunoprecipitation followed by high-throughput DNA sequencing; Pilot effort to for Biotechnology determine the methylation status of CpG-rich regions. Michael Snyder Stanford University Identify transcription factor binding sites using chromatin immunoprecipitation followed by high-throughput DNA sequencing. John Stamatoyannopoulos University of Map and functionally classify DNaseI hypersensitive sites by digital DNaseI and histone modification mapping using high-throughput
    [Show full text]
  • National Human Genome Research Institute EA Feingold, PJ G
    ENCODE Project Consortium ENCODE Project Scientific Management: National Human Genome Research Institute E. A. Feingold,1 P. J. Good,1 M. S. Guyer,1 S. Kamholz,1 L. Liefer,1 K. Wetterstrand,1 F. S. Collins2 Initial ENCODE Pilot Phase Participants: Affymetrix, Inc. T. R. Gingeras,3 D. Kampa,3 E. A. Sekinger,4 J. Cheng,3 H. Hirsch,4 S. Ghosh,3 Z. Zhu,5 S. Patel,3 A. Piccolboni,3 A. Yang,4 H. Tammana,3 S. Bekiranov,3 P. Kapranov,3 R. Harrison,5 G. Church,5 K. Struhl4; Ludwig Institute for Cancer Research B. Ren,6 T. H. Kim,6 L. O. Barrera,6 C. Qu,6 S. Van Calcar,6 R. Luna,7 C. K. Glass,7 M. G. Rosenfeld8; Municipal Institute of Medical Research R. Guigó,9 S. E. Antonarakis,10 E. Birney,11 M. Brent,12 L. Pachter,13 A. Reymond,10,14 E. T. Dermitzakis,15 C. Dewey,16 D. Keefe,11 F. Denoeud,9 J. Lagarde,9 J. Ashurst,15 T. Hubbard,15 J. J. Wesselink,9 R. Castelo,9 E. Eyras9; Stanford University R. M. Myers,17 A. Sidow,17,18 S. Batzoglou,19 N. D. Trinklein,17 S. J. Hartman,17 S. F. Aldred,17 E. Anton,17 D. I. Schroeder,20 S. S. Marticke,17 L. Nguyen,17 J. Schmutz,21 J. Grimwood,21 M. Dickson,21 G. M. Cooper,17 E. A. Stone,17 G. Asimenos,19 M. Brudno19; University of Virginia A. Dutta,22 N. Karnani,22 C. M. Taylor,22,23 H. K. Kim,22 G.
    [Show full text]
  • Multiple Genes Encode Nuclear Factor 1-Like Proteins That Bind To
    Proc. Nati. Acad. Sci. USA Vol. 85, pp. 8%3-8967, December 1988 Biochemistry Multiple genes encode nuclear factor 1-like proteins that bind to the promoter for 3-hydroxy-3-methylglutaryl-coenzyme A reductase (transcription factors/DNA-binding proteins/regulation of cholesterol metabolism) GREGORIO GIL*t, JEFFREY R. SMITH*, JOSEPH L. GOLDSTEIN*, CLIVE A. SLAUGHTERS, KIM ORTHIt, MICHAEL S. BROWN*, AND TIMOTHY F. OSBORNE* *Departments of Molecular Genetics and Internal Medicine and *Howard Hughes Medical Institute, University of Texas Southwestern Medical Center, 5323 Hary Hines Boulevard, Dallas, TX 75235 Contributed by Michael S. Brown, August 31, 1988 ABSTRACT DNA-binding proteins of the nuclear factor 1 62,000. Santoro et al. (3) isolated three cDNAs for NF1/CTF (NF1) family recognize sequences containing TGG. Two of proteins from human HeLa cells. All of the mRNAs were these proteins, termed reductase promoter factor (RPF) pro- derived from a single gene by alternative splicing and differed teins A and B, bind to the promoter for hamster 3- by the presence or absence ofan insertion in the middle ofthe hydroxy-3-methylglutaryl-coenzyme A reductase, a negatively protein and the presence of various COOH termini. All three regulated enzyme in cholesterol biosynthesis. In the current proteins, when produced in Escherichia coli, bound to the study, we determined the sequences of peptides derived from NF1/CTF recognition sequence, and at least two of them hamster RPF proteins A and B and used this information to stimulated replication of adenovirus in vitro. isolate a cDNA, designated pNF1/Redl, that encodes RPF Another member of the NF1/CTF family is the TGGCA- protein B.
    [Show full text]
  • Snyder Produc&On Group Summary for ENCODE 3
    Snyder Producon Group Summary for ENCODE 3 Nathaniel Watson, Jessika Adrian, Tejaswini Mishra, Minyi Shi, Denis Salins, Trup Kawli, Michael Snyder Department of Gene,cs September 22, 2016 About ENCODE Snyder DPC: Released Work THE ENCYCLOPEDIA OF DNA ELEMENTS, or ENCODE, is an MAJOR RESEARCH GOALS: To Identify transcription factor WE HAVE POSITIVELY CHARACTERIZED ANTIBODIES for 302 international project that has been funded by NHGRI since its pilot binding sites in the human genome, and functionally targets spanning 14 cell lines and 10 bodily tissues; see Fig. 2. Not phase initiated in 2003, with the goal of identifying all functional characterize regulatory elements.! shown in Fig. 2 are 731 negative antibody characterizations that elements in the human genome.! have been submitted to the ENCODE Portal. ! Four Phases of the ENCODE Project! EXPERIMENTS range from ChIP-Seq, siRNA-Seq, ATAC-Seq, as well as ChIA-PET; see Fig. 1.! Sep. 2003 Sep. 2007 Sep. 2013 Feb. 2017 Number of Targets With Posi3ve An3body Pilot Phase I Phase II Phase III Phase IV Number of Released Experiments in Phase III Characterizaons for each Cell or Tissue Type in 500 ENCODE 3 450 500 400 450 THE CONSORTIUM is composed of multiple Data Production Centers 400 (DPCs), a central Data Coordination Center (DCC), and a central 350 350 Data Analysis Center (DAC).! 300 2016 300 250 250 2015 200 200 150 2014 150 100 100 50 50 0 0 ChIP-Seq ATAC-Seq ChIA-PET siRNA-Seq K562 liver A549 heart HeLa MCF-7 HepG2 Other HeLa-S3 IMR-90 Figure 1. The number of experiments performed in the Snyder DPC in GM12878 HEK293T ENCODE 3 that have been released to the public by the DCC.
    [Show full text]