DOCSLIB.ORG

The Measurement of Loudness*

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Measurement of Loudness* THE JOURNAL OF THE ACOUSTICAL SOCIETY OF AMERICA Volume27Number5 SEPTEMBER. 1955 The Measurement of Loudness* S.S. STEVENS Psycho-AcousticLaboratory, Harvard University,Cambrfigge, Massachusetts (ReceivedJune 17, 1955) This paperreviews the availableevidence (published and unpublished)on the relationbetween loudness and stimulusintensity. The e.vidence suggests that for the typical listenerthe loudnessL of a 1000-cycle tone can be approximatedby a powerfunction of intensity I, of which the exponentis log•02.The equation is: L--kI ø.a.Intensity here is assumedto be proportionalto the squareof the soundpressure. In terms of sones,where 1 soneis the loudnessproduced by a tone at 40 db above the standardreference level, the equationfor loudnessL as a function of the number of decibelsN becomes'logL=0.03N--1.2. Otherwisesaid, a loudnessratio of 2:1 is producedby a pair of stimuli that differ by 10 db, and this re- lation appearsto hold over the entire range of audibleintensities. At low levelsof intensity,the loudnessof white noisegrows more rapidly than the loudnessof a 1000-cycle tone, but abovethe level of approximately50 db the two loudnessesremain more nearly proportional.The suggestionis madethat for all levelsgreater than 50 db the loudnessof continuousnoises may be calculated from the equation:logL=O.O3N-t--S, where $ is a spectrumparameter to be determinedempirically. HE purposeof this reviewis to examinethe the nature of the central issue. What we want to know availabledata on the measurementof subjective is how loud variousstimuli soundto people.By this we loudness.It is hoped that by assemblingthe relevant mean, perforce,what do people say when they try to informationin one place we may be able to reach a describeloudness in quantitative terms?In askingthis reasonableconclusion concerning the relation between questionwe are not at the outset trying to solve the loudnessand intensity.The variousresults obtained by problem of how the ear works or how the nervous workersin this fieldmake it plain that the scalerelating systemperforms its integrations.We are not trying to loudnessto intensity is not somethingthat can be countnerve impulses nor provea theory.We are merely determinedwith high precision,but these efforts also looking for the empirical answer to a very empirical make it plain that peopleare able to make quantitative question'How do peopledescribe sounds when we ask estimates of loudness and that it is not unreasonable to them to usea numericallanguage instead of adjectives? try to determinea loudnessscale that will be representa- Our interestin askingthis questionmay be academic tive of the typical listener. or it may be practical.The academicside of the issue Despite its many pitfalls, I think we can probably hasa long historyfull of side-takingand polemics.• The make senseof this problemprovided we are sufficiently practicalside of the problemhad its originin acoustical modestin our demands.Not only mustwe renouncethe engineering.Not long after they had developedthe hopefor highprecision, but alsowe mustkeep in mind conventionaldecibel scale for measuringsound inten- sity, the engineersnoted that equalsteps on the decibel * This work was carried out under Contract N5ori-76 between Harvard Universityand the Officeof Naval Research,U.S. Navy scaledo not soundlike equalsteps, and that a level of (ProjectNR142-201, Report PNR-168). Reproductionfor any purposeof the U.S. Governmentis permitted. • E.G. Boring,Am. J. Psychol.32, 449-471 (1921). 815 Redistribution subject to ASA license or copyright; see http://acousticalsociety.org/content/terms. Download to IP: 165.123.230.136 On: Tue, 25 Aug 2015 06:45:44 816 S. S. STEVENS 50 db does not sound like half of 100 db. Since the periment.Thus bisectionmight providea test of the engineeroften faces the problemof communicatingwith generalityof a ratio scale,but by itselfbisection cannot a customer, it was soon realized that there was a need generate a ratio scale. for a scale whose numbers would make more sense to In the tabulationsthat follow only the resultsob- the customer than do the numbers on the decibel scale. tainedby magnitudeestimation and ratio determination The generationof a loudnessscale is in principle will be considered. quite simple.All we need to do is producean array of Magnitudeestimation means the following:A stand- soundsand ask a groupof listenersto assignnumbers to ard tone is presentedand an arbitrary number is as- thesesounds in sucha way that the numbersreflect the signedto its loudness,e.g., 1 or 100.Then a comparison perceivedloudness of the sounds.In practice,of course, tone is presented,and the subjectdecides what number it turns out that many alternative techniquesare pos- he thinks shouldbe assignedto the loudnessof the com- sible, and that subtle differencesin experimentalpro- parison stimulus.Under another versionof the method cedure sometimesinfluence what the listener says or of magnitude estimation, the standard is omitted does. When the listener tries to tell us about the relative entirely.The subjecthears a seriesof intensitiespre- loudnessof two sounds,he is subjectto a host of poten- sented in random order, and to these intensities he tially biasing factors. Some of these factors are built assignsnumbers proportioned to theirapparent loudness. into the listener;someare suppliedby the experimenter. Ratio determinationmeans those procedures that aim Someare easyto discover;others are as elusiveas foxes to discoverwhat intensityproduces a loudnessbearing in a forest. The parametersthat affect experimentson a prescribedratio to a givenloudness. The ratio may be loudnessare numerousand sometimesso conflicting that a fraction or a multiple of the standard. it may be impossibleunder any one procedureto opti- We can further divide the method of ratio determina- mize all of them. Consequently,the definitive experi- tion into two classes'(1) The subjectis allowedto ment in this field, if we may hopefor such,will probably adjust the intensity to produce the desired ratio needto involvea multipleattack of the sort that might (methodof adjustment).(2) The experimentersets the balance out the various sources of distortion and bias. intensityand asksthe subjectto say whetherit is too Nevertheless, under a wide variety of conditions highor too low (methodof constantstimuli). Of course, rather similar results continue to be obtained. Provided from a seriesof magnitudeestimations a ratio deter- we are willing to be content with modestprecision, we minationcan be made by a processof interpolation. can predict pretty well what the averagelistener will Consequently,it is possibleto combinethe resultsof say about loudnessin most ordinary situations.It is experimentsthat usethese two differentprocedures. my own beliefthat this predictabilityis sufficientlyhigh Each of these methodshas its advantagesand its to justify the standardizationof a loudnessscale to disadvantages.And, of course,each has many sub- representfor the "standardobserver" the relation be- varieties, someof which are better or worsethan others. tween loudnessand intensity. Merits of the Methods METHODS Let me try to list someof the assetsand liabilities of Three principal methodshave been used to obtain these methods as they seem to be disclosedin the direct estimates of the relation between loudness and studiesof other experimentersand in our work at the intensity:bisection (or equisection),ratio determination Psycho-AcousticLaboratory. (includingfractionation), and direct magnitudeestima- tion. Methods that involve the comparisonof one-rs- Methodof MagnitudeEstimation (ME) two tones and one-rs-two ears are not included here This is the mostdirect and, in someways, the most becausethey rest on assumptionsthat can be tested efficientmethod. Each presentationof the stimulusis only by the direct comparisontechniques that are re- rated numerically,and no information need be thrown quiredto establisha loudnessscale in the first place. The methodof bisection,involving the determination away. Like all procedures,the method of magnitude estimation is susceptibleto various biases, some of of the loudnessthat lies midway between two given whichcan probably be avoidedor counterbalanced.One loudnesses,has its limitations, owing principally to the biasarises from the fact that the subject'sestimates are fact that it leadsonly to an interval scale2 (analogous to the temperaturescales, Fahrenheit and Celsius).Its influencedby the order in which the stimuli are pre- sented. Since the subject usually tries to be self-con- resultsdo not allowus to setup a ratio scale(analogous sistent,what he saysabout a givencomparison stimulus to scalesof weight and length). Ratio scalescan, in dependsto someextent on what he has said about the principle,be determinedby the methodsof fractionation precedingones. This particular bias doesnot affect the and magnitudeestimation, and suchratio scalescan be first judgment he makes, however, and it is therefore usedto predictwhat oughtto happenin a bisectionex- instructiveto comparethese first judgmentswith the • S.S. Stevens, editor, Handbookof ExperimentalPsychology later ones.Actually, thesefirst judgmentsare usually (John Wiley and Sons,Inc., New York, 1951),Chap. 1. consistent with the later ones. Redistribution subject to ASA license or copyright; see http://acousticalsociety.org/content/terms. Download to IP: 165.123.230.136 On: Tue, 25 Aug 2015 06:45:44 MEASUREMENT OF LOUDNESS 817 Another bias arisesfrom the fact that, although the potentiometerso that the
Load more

Recommended publications
  • Ebm-Papst Mulfingen Gmbh & Co. KG Postfach 1161 D-74671 Mulfingen
    ebm-papst Mulfingen GmbH & Co. KG Postfach 1161 D-74671 Mulfingen Internet: www.ebmpapst.com E-mail: [email protected] Editorial contact: Katrin Lindner, e-mail: [email protected] Phone: +49 7938 81-7006, Fax: +49 7938 81-665 Focus on psychoacoustics How is a fan supposed to sound? Our sense of hearing works constantly and without respite, so our ears receive noises 24 hours a day. About 15,000 hair cells in the inner ear catch the waves from every sound, convert them to signals and relay the signals to the brain, where they are processed. This is the realm of psychoacoustics, a branch of psychophysics. It is concerned with describing personal sound perception in relation to measurable noise levels, i.e. it aims to define why we perceive noises as pleasant or unpleasant. Responsible manufacturers take the results of relevant research into account when developing fans. When we feel negatively affected by a sound, for example when it disturbs us, we call it noise pollution. Whether this is the case depends on many factors (Fig. 1). Among other things, our current situation plays a role, as do the volume and kind of sound. The same is true of fans, which need to fulfill different requirements depending on where they are used. For example, if they are used on a heat exchanger in a cold storage facility where people spend little time, low volume or pleasant sound is not an issue. But ventilation and air conditioning units in living and working areas have to meet much different expectations.
    [Show full text]
  • Decibels, Phons, and Sones
    Decibels, Phons, and Sones The rate at which sound energy reaches a Table 1: deciBel Ratings of Several Sounds given cross-sectional area is known as the Sound Source Intensity deciBel sound intensity. There is an abnormally Weakest Sound Heard 1 x 10-12 W/m2 0.0 large range of intensities over which Rustling Leaves 1 x 10-11 W/m2 10.0 humans can hear. Given the large range, it Quiet Library 1 x 10-9 W/m2 30.0 is common to express the sound intensity Average Home 1 x 10-7 W/m2 50.0 using a logarithmic scale known as the Normal Conversation 1 x 10-6 W/m2 60.0 decibel scale. By measuring the intensity -4 2 level of a given sound with a meter, the Phone Dial Tone 1 x 10 W/m 80.0 -3 2 deciBel rating can be determined. Truck Traffic 1 x 10 W/m 90.0 Intensity values and decibel ratings for Chainsaw, 1 m away 1 x 10-1 W/m2 110.0 several sound sources listed in Table 1. The decibel scale and the intensity values it is based on is an objective measure of a sound. While intensities and deciBels (dB) are measurable, the loudness of a sound is subjective. Sound loudness varies from person to person. Furthermore, sounds with equal intensities but different frequencies are perceived by the same person to have unequal loudness. For instance, a 60 dB sound with a frequency of 1000 Hz sounds louder than a 60 dB sound with a frequency of 500 Hz.
    [Show full text]
  • Guide for the Use of the International System of Units (SI)
    Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S.
    [Show full text]
  • Psychoacoustics and Its Benefit for the Soundscape
    ACTA ACUSTICA UNITED WITH ACUSTICA Vol. 92 (2006) 1 – 1 Psychoacoustics and its Benefit for the Soundscape Approach Klaus Genuit, André Fiebig HEAD acoustics GmbH, Ebertstr. 30a, 52134 Herzogenrath, Germany. [klaus.genuit][andre.fiebig]@head- acoustics.de Summary The increase of complaints about environmental noise shows the unchanged necessity of researching this subject. By only relying on sound pressure levels averaged over long time periods and by suppressing all aspects of quality, the specific acoustic properties of environmental noise situations cannot be identified. Because annoyance caused by environmental noise has a broader linkage with various acoustical properties such as frequency spectrum, duration, impulsive, tonal and low-frequency components, etc. than only with SPL [1]. In many cases these acoustical properties affect the quality of life. The human cognitive signal processing pays attention to further factors than only to the averaged intensity of the acoustical stimulus. Therefore, it appears inevitable to use further hearing-related parameters to improve the description and evaluation of environmental noise. A first step regarding the adequate description of environmental noise would be the extended application of existing measurement tools, as for example level meter with variable integration time and third octave analyzer, which offer valuable clues to disturbing patterns. Moreover, the use of psychoacoustics will allow the improved capturing of soundscape qualities. PACS no. 43.50.Qp, 43.50.Sr, 43.50.Rq 1. Introduction disturbances and unpleasantness of environmental noise, a negative feeling evoked by sound. However, annoyance is The meaning of soundscape is constantly transformed and sensitive to subjectivity, thus the social and cultural back- modified.
    [Show full text]
  • Brightness and Loudness As Functions of Stimulus Duration
    Brightness and loudness as functions of stimulus duration 1 JOSEPH C, STEVENS AND JAMES W. HALL LABORATORY OF PSYCHOPHYSICS. HARVARD UNIVERSiTY The brightness of white light and the loudness of white (1948) and by Small, Brandt, and Cox (1962) for white noise were measured by magnitude estimation for sets of noise. White noise provides a more suitable stimulus stimuli that varied in intensity and duration. Brightness and for this kind of problem than pure tones, because the loudness both grow as power functions of duration up to a intensity of a white noise (unlike tones) can be rapidly critical duration, beyond which apparent magnitude is es­ modulated without effecting a material change in the sentially independent of duration. For brightness, the critical sound spectrum. Thus a prominent click is heard at duration decreases with increasing intensity, but for loudness the onset of a tone but not at the onset of a noise. the critical duration is nearly constant at about ISO msec. How the loudness of white noise grows with intensity Loudness and brightness also grow as power functions of in­ has been the subject of several investigations (S. S. tensity. The loudness exponent is the same for all durations, Stevens, 1966a). Like brightness, the loudness of white but the brightness exponent is about half again as large for noise obeys the general psychophysical power law short durations as for long. The psychophysical power func­ proposed by S. S. Stevens (1961) tions were used to generate equal-loudness and equal-bright­ IjJ ~ k¢.8 (1) ness functions, which specify the combinations of intensity E and duration T that produce the same apparent magnitude.
    [Show full text]
  • Comparison of Loudness Calculation Procedure Results to Equal Loudness Contours
    University of Windsor Scholarship at UWindsor Electronic Theses and Dissertations Theses, Dissertations, and Major Papers 2010 Comparison of loudness calculation procedure results to equal loudness contours Jeremy Charbonneau University of Windsor Follow this and additional works at: https://scholar.uwindsor.ca/etd Recommended Citation Charbonneau, Jeremy, "Comparison of loudness calculation procedure results to equal loudness contours" (2010). Electronic Theses and Dissertations. 5428. https://scholar.uwindsor.ca/etd/5428 This online database contains the full-text of PhD dissertations and Masters’ theses of University of Windsor students from 1954 forward. These documents are made available for personal study and research purposes only, in accordance with the Canadian Copyright Act and the Creative Commons license—CC BY-NC-ND (Attribution, Non-Commercial, No Derivative Works). Under this license, works must always be attributed to the copyright holder (original author), cannot be used for any commercial purposes, and may not be altered. Any other use would require the permission of the copyright holder. Students may inquire about withdrawing their dissertation and/or thesis from this database. For additional inquiries, please contact the repository administrator via email ([email protected]) or by telephone at 519-253-3000ext. 3208. Comparison of Loudness Calculation Procedure Results to Equal Loudness Contours By Jeremy Charbonneau A Thesis Submitted to the Faculty of Graduate Studies and Research through Mechanical Engineering
    [Show full text]
  • Intensity of Sound
    01/02 Intensity - 1 INTENSITY OF SOUND The objectives of this experiment are: • To understand the concept of sound intensity and how it is measured. • To learn how to operate a Sound Level Meter APPARATUS: Radio Shack Sound Level Meter, meterstick, function generator, headphones. INTRODUCTION Sound energy is conveyed to our ears (or instruments) by means of a wave motion through some medium (gas, liquid, or solid). At any given point in the medium the energy content of the wave disturbance varies as the square of the amplitude of the wave motion. That is, if the amplitude of the oscillation is doubled the energy of the wave motion is quadrupled. The common method in gauging this energy transport is to measure the rate at which energy is passing a certain point. This concept involves sound intensity. Consider an area that is normal to the direction of the sound waves. If the area is a unit, namely one square meter, the quantity of sound energy expressed in Joules that passes through the unit area in one second defines the sound intensity. Recall the time rate of energy transfer is called "power". Thus, sound intensity is the power per square meter. The common unit of power is the watt ( 1w = 1 Joules/s). Normally, sound intensity is measured as a relative ratio to some standard intensity, Io. The response of the human ear to sound waves follows closely to a logarithmic function of the form R = k log I , where R is the response to a sound that has an intensity of I, and k is a constant of proportionality .
    [Show full text]
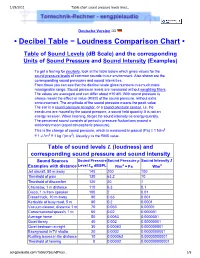
  • Table Chart Sound Pressure Levels Level Sound Pressure
    1/29/2011 Table chart sound pressure levels level… Deutsche Version • Decibel Table − Loudness Comparison Chart • Table of Sound Levels (dB Scale) and the corresponding Units of Sound Pressure and Sound Intensity (Examples) To get a feeling for decibels, look at the table below which gives values for the sound pressure levels of common sounds in our environment. Also shown are the corresponding sound pressures and sound intensities. From these you can see that the decibel scale gives numbers in a much more manageable range. Sound pressure levels are measured without weighting filters. The values are averaged and can differ about ±10 dB. With sound pressure is always meant the effective value (RMS) of the sound pressure, without extra announcement. The amplitude of the sound pressure means the peak value. The ear is a sound pressure receptor, or a sound pressure sensor, i.e. the ear-drums are moved by the sound pressure, a sound field quantity. It is not an energy receiver. When listening, forget the sound intensity as energy quantity. The perceived sound consists of periodic pressure fluctuations around a stationary mean (equal atmospheric pressure). This is the change of sound pressure, which is measured in pascal (Pa) ≡ 1 N/m2 ≡ 1 J / m3 ≡ 1 kg / (m·s2). Usually p is the RMS value. Table of sound levels L (loudness) and corresponding sound pressure and sound intensity Sound Sources Sound PressureSound Pressure p Sound Intensity I Examples with distance Level Lp dBSPL N/m2 = Pa W/m2 Jet aircraft, 50 m away 140 200 100 Threshold of pain
    [Show full text]
  • Sound Sense – by D. Lovegrove, S. Hough
    SOUND (QUALITY) SENSE Many of us would agree that there are a lot of things around us that are too noisy, such as the seats behind the engines on a long flight, an angry two-year-old and the volume of the music system in the car next to us at the stoplight, which shakes our seats. Sometimes, though, it’s not the loudest sounds that are the hardest to live with. It’s the intermittent hiss, or the whine perfectly pitched to set our teeth on edge. When a product or an appliance is manufactured, a vehicle, a toy, a train carriage, anything that people are going to hear or be near, it should sound “right”. Not just quiet enough to be unobjectionable - that’s necessary but not sufficient. It’s got to have that indefinable Sound of Quality, the sound you would wish your car door in closing would make. A truism of sound quality work is that a good lawnmower doesn’t sound like a good refrigerator. Companies who take this sort of thing seriously do jury testing. They may use listeners like their customers to get a better measure of public opinion, or listeners from among their engineers, to gain a better understanding of which elements of the product are making the most objectionable part of the noise. The jury ranks noises according to various rules. The 2 most successful forms of comparison are “Paired Comparison” and “Semantic Differential”. The use of a Fixed Scale (“On a scale of 1-10, how annoying is this noise?”) is generally not recommended.
    [Show full text]
  • FESI DOCUMENT A2 Basics of Acoustics
    FESI DOCUMENT A2 Basics of Acoustics September 2001, 3rd revised edition to be ordered: Thermal Insulation Contractors Association Mr. Ralph Bradley Tica House Allington Way Yarm Road Business Park Darlington DLI 4QB Tel : +44 (0) 1325 734140 direct Fax: +44 (0) 1325 466704 www.tica-acad.co.uk [email protected] Basics of Acoustics Contents A2-0 Intention .......................................................................................................................................2 A2-1 Introduction ..................................................................................................................................2 A2-2 Classification................................................................................................................................3 A2-2.1 Sound Sensation .........................................................................................................................4 A2-2.2 Infrasonic, Audible and Ultrasonic Sound ...................................................................................6 A2-2.3 Airborne, Structureborne, Waterborne Sound.............................................................................7 A2-2.4 Acoustic Insulation and Sound Attenuation.................................................................................8 A2-3 Physical, technical basics............................................................................................................8 A2-3.1 Frequency, Speed of Sound, Wavelength...................................................................................8
    [Show full text]
  • PETERSEN-THESIS-2018.Pdf (1.655Mb)
    AN INVESTIGATION OF SOUND MEASUREMENT CHANGES RESULTING FROM MODIFICATIONS TO A SEMI-REVERBERANT SOUND CHAMBER A Thesis by MICHELLE ANNE PETERSEN Submitted to the Office of Graduate and Professional Studies of Texas A&M University in partial fulfillment of the requirements for the degree of MASTER OF SCIENCE Chair of Committee, Michael B. Pate Committee Members, Harry A. Hogan Maria D. King Head of Department, Andreas A. Polycarpou December 2018 Major Subject: Mechanical Engineering Copyright 2018 Michelle Anne Petersen ABSTRACT The RELLIS Energy Efficiency Laboratory, REEL, is a research and testing facility established in 1939 and an approved testing laboratory for HVI. Testing of residential ventilation devices is one of the main applications of this laboratory. Recently, the microphones for the sound chamber were changed from free-field to diffuse. The test method and procedure for measuring sones is understood, but the effect of using a different microphone type to record sound pressure levels is not. The need to understand the effects of changing equipment in sound facilities is necessary in order to provide accurate and verifiable test results. This study investigates the change in sone ratings between free-field and diffuse microphones by using the sound facilities at REEL. A total of 96 trials for eight different residential ventilation devices was performed to record sone levels over a range of less than 0.3 to 11.5 rated sones. This analysis found that there was less than a 4% difference in sone values measured when using the different microphone types. Additionally, the change in sone ratings using different resonant sound sources (RSS) was analyzed using the same data from the 96 trials.
    [Show full text]
  • Precise and Full-Range Determination of Two-Dimensional Equal Loudness Contours
    ＩＳ－０１ Precise and Full-range Determination of Two-dimensional Equal Loudness Contours Research Coordinator: Yôiti Suzuki (Research Institute of Electrical Communication, Tohoku University: Japan) Research Team Members: Volker Mellert (Oldenburg University: Germany) Utz Richter (Physikalisch-Technische Bundesanstalt: Germany) Henrik Møller (Aalborg University: Denmark) Leif Nielsen (Danish Standards Association: Denmark) Rhona Hellman (Northeastern University: U.S.A.) Kaoru Ashihara (National Institute of Advanced Industrial Science and Technology: Japan) Kenji Ozawa (Yamanashi University: Japan) Hisashi Takeshima (Sendai National College of Technology: Japan) Duration: April, 2000 ～ March, 2003 Abstract: The equal-loudness contours describe the frequency characteristic of sensitivity of our auditory system. A set of the equal-loudness contours based on British data measured in mid-1950 was standardized as ISO 226. However, several research results reported in mid-1980 showed that the set of equal-loudness contours in ISO 226 contained a large error. We, therefore, carried out this project to determine new precise and comprehensive equal-loudness contours and to fully revise the ISO 226. New equal-loudness contours were based on the data of 12 studies, mostly from measurements by the members of this team, reported since 1983. These contours were calculated using a model based on knowledge of our auditory system. Based on the research results, draft standards of the new equal-loudness contours were made and proposed to ISO/TC 43 (Acoustics). The new standard finally was established on August 2003. 1. Introduction An equal-loudness contour is a curve that ties up sound pressure levels having equal loudness as a function of frequency. In other words, it expresses a frequency characteristic of loudness sensation.
    [Show full text]