Abstract T Authors
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Women's 3000M Steeplechase
Games of the XXXII Olympiad • Biographical Entry List • Women Women’s 3000m Steeplechase Entrants: 47 Event starts: August 1 Age (Days) Born SB PB 1003 GEGA Luiza ALB 32y 266d 1988 9:29.93 9:19.93 -19 NR Holder of all Albanian records from 800m to Marathon, plus the Steeplechase 5000 pb: 15:36.62 -19 (15:54.24 -21). 800 pb: 2:01.31 -14. 1500 pb: 4:02.63 -15. 3000 pb: 8:52.53i -17, 8:53.78 -16. 10,000 pb: 32:16.25 -21. Half Mar pb: 73:11 -17; Marathon pb: 2:35:34 -20 ht EIC 800 2011/2013; 1 Balkan 1500 2011/1500; 1 Balkan indoor 1500 2012/2013/2014/2016 & 3000 2018/2020; ht ECH 800/1500 2012; 2 WSG 1500 2013; sf WCH 1500 2013 (2015-ht); 6 WIC 1500 2014 (2016/2018-ht); 2 ECH 3000SC 2016 (2018-4); ht OLY 3000SC 2016; 5 EIC 1500 2017; 9 WCH 3000SC 2019. Coach-Taulant Stermasi Marathon (1): 1 Skopje 2020 In 2021: 1 Albanian winter 3000; 1 Albanian Cup 3000SC; 1 Albanian 3000/5000; 11 Doha Diamond 3000SC; 6 ECP 10,000; 1 ETCh 3rd League 3000SC; She was the Albanian flagbearer at the opening ceremony in Tokyo (along with weightlifter Briken Calja) 1025 CASETTA Belén ARG 26y 307d 1994 9:45.79 9:25.99 -17 Full name-Belén Adaluz Casetta South American record holder. 2017 World Championship finalist 5000 pb: 16:23.61 -16. 1500 pb: 4:19.21 -17. 10 World Youth 2011; ht WJC 2012; 1 Ibero-American 2016; ht OLY 2016; 1 South American 2017 (2013-6, 2015-3, 2019-2, 2021-3); 2 South American 5000 2017; 11 WCH 2017 (2019-ht); 3 WSG 2019 (2017-6); 3 Pan-Am Games 2019. -

COPA DE EUROPA DE CLUBES - Grupo a Albufeira (POR) 26/27 Mayo 2007
COPA DE EUROPA DE CLUBES - Grupo A Albufeira (POR) 26/27 mayo 2007 HOMBRES 7.13/+0,1 - 6. Darragh O’Farrell GBR 7.09/+0,7 - 7. Koray Imrak Clasificación: TUR 6.89/+0,9 1. Sports Luch Moscow RUS 110 2. Sporting Clube Portugal POR 84 Triple (27): 1. Yevgeniy Plotnir RUS 16.96/+3,4 (16.58/+1,7) - 2. 3. Puma Chapín Jerez ESP 84 Dmitrij Valukevic SVK 16.72/+1,1 - 3. Andrés Capellán ESP 4. Fiamme Gialle Rome ITA 77 16.00/+3,3 (15.58/+1,7) - 4. Américo Castelobranco POR 15.59/+2,2 5. AK Spartak Dubnica SVK 74 - 5. Matteo Pusceddu ITA 15.49/+3,0 (14.47/+1,3) - 6. Hasim Yilmaz 6. Fenerbahce Spor Kulubu TUR 69 TUR 15.25/+4,0 - 7. Gary Wilson GBR 14.57/+3,7 7. Belgrave Harriers GBR 59 Peso (26): 1. Yuri Bilonog POR (BLR) 19.68 - 2. Grigoriy Panfilov 100m (-1,6) (26): 1. Francis Obikwelu POR 10.23 - 2. Ángel David RUS 19.52 - 3. Manuel Martínez ESP 18.74 - 4. Chris Gearing GBR Rodríguez ESP 10.35 - 3. Andrey Yepishin RUS 10.38 - 4. Simone 17.90 - 5. Daniel Vanek SVK 17.68 - 6. Huseyin Atici TUR 17.21 - 7. Collio ITA 10.42 - 5. Wade Bennnett-Jackson GBR 10.64 - 6. Ismail Eugenio Umberto Mannucci ITA 16.31 Aslan TUR 10.74 - 7. Jozef Svondrk SVK 11.06 Disco (27): 1. Aleksandr Borichevskiy RUS 60.96 - 2. Ercument 200m (+2,0) (27): 1. Francis Obikwelu POR 20.93 - 2. -
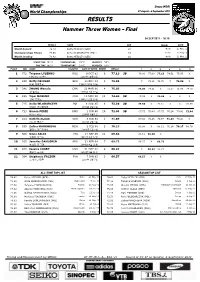
AT-HT-W-F--A--.RS1.Pdf
Daegu (KOR) World Championships 27 August - 4 September 2011 RESULTS Hammer Throw Women - Final 04 SEP 2011 - 18:15 RESULT NAME AGE VENUE DATE World Record 79.42 Betty HEIDLER (GER) 28 Halle 21 May 11 Championships Record 77.96 Anita WLODARCZYK (POL) 24 Berlin 22 Aug 09 World Leading 79.42 Betty HEIDLER (GER) 28 Halle 21 May 11 START TIME 18:10 TEMPERATURE 28°C HUMIDITY 54% END TIME 19:37 TEMPERATURE 27°C HUMIDITY 54% PLACE BIB NAME COUNTRY DATE OF BIRTH ORDER RESULT 1 2 3 4 5 6 1 772 Tatyana LYSENKO RUS 9 OCT 83 6 77.13 SB 76.80 77.09 77.13 74.51 75.05 X 타티아나 리센코 1983년 10월 9일 2 420 Betty HEIDLER GER 14 OCT 83 3 76.06 X 73.96 74.70 X 76.06 X 베티 하이들러 1983년 10월 14일 3 246 ZHANG Wenxiu CHN 22 MAR 86 4 75.03 75.03 74.31 X 73.17 71.86 74.79 장 웬시우 1986년 3월 22일 4 285 Yipsi MORENO CUB 19 NOV 80 12 74.48 SB 73.29 X 74.48 X X X 입시 모레노 1980년 11월 19일 5 715 Anita WLODARCZYK POL 8 AUG 85 8 73.56 SB 73.56 X 72.61 X X 72.65 아니타 볼다르치크 1985년 8월 8일 6 733 Bianca PERIE ROU 1 JUN 90 10 72.04 SB 67.73 70.40 67.75 70.24 70.91 72.04 비앙카 페리 1990년 6월 1일 7 424 Kathrin KLAAS GER 8 FEB 84 1 71.89 67.02 70.18 70.67 71.89 70.44 X 카트린 클라스 1984년 2월 8일 8 650 Zalina MARGHIEVA MDA 5 FEB 88 5 70.27 69.99 X 68.13 70.24 70.27 68.76 잘리나 마르기에바 1988년 2월 5일 9 506 Silvia SALIS ITA 17 SEP 85 11 69.88 68.61 69.88 X 실비아 살리스 1985년 9월 17일 10 105 Jennifer DAHLGREN ARG 21 APR 84 7 69.72 68.27 X 69.72 헤니퍼 달그렌 1984년 4월 21일 11 928 Jessica COSBY USA 31 MAY 82 9 68.91 X 68.91 68.15 제시카 코스비 1982년 5월 31일 12 364 Stéphanie FALZON FRA 7 JAN 83 2 66.57 66.57 X X 스테파니 팔존 1983년 1월 7일 ALL-TIME TOP LIST -

Italia / Italy
XIII IAAF World Championships Daegu (KOR) - 27 agosto-4 settembre Italia / Italy I componenti della staffetta 4x100 azzurra medaglia d’argento agli Europei 2010 di Barcellona The Italian 4x100 team, silver medallist at the 2010 European Championships of Brarelona La Delegazione The Delegation FIDAL La Delegazione / The Delegation Federazione Italiana Alberto Morini Capo Delegazione / Head of the Delegation di Atletica Leggera Franco Angelotti Consigliere Addetto / Council Member Italian Athletics Federation Francesco Uguagliati Direttore Tecnico / Technical Director Via Flaminia Nuova, 830 00191 Roma, Italia Vittorio Visini Assistente D.T. / Assistant to TD www.fidal.it Rita Bottiglieri Team Manager Francesco Cuccotti Team Manager Presidente /President Marco Sicari Addetto Stampa / Press Officer Franco Arese Pierluigi Fiorella Medico / Doctor Giuseppe Fischetto Medico / Doctor Consiglieri Antonio Abbruzzese Fisioterapista / Physio Council Members Maria M. Marello Fisioterapista / Physio Alberto Morini (Vice Presidente Vicario / Senior Vice President ) Filippo Di Mulo Tecnico / Coach Adriano Rossi (Vice Presidente / Giuseppe Mannella Tecnico / Coach Vice President ) Roberto Pericoli Tecnico / Coach Stefano Andreatta Fabio Pilori Tecnico / Coach Franco Angelotti Roberto Piscitelli Tecnico / Coach Marcello Bindi Nicola Silvaggi Tecnico / Coach Giovanni Caruso Angelo Zamperin Tecnico / Coach Alessandro Castelli Augusto D’agostino Michele Basile Tecnico Personale / Personal Coach Francesco De Feo Riccardo Ceccarini Tecnico Personale / Personal -

News from France 03.10
http://www.ambafrance-us.org http://www.france.diplomatie.gouv.fr VOL. 03.10 SEPTEMBER 24, 2003 A review of news and trends in France France and Germany Unite to Boost Growth INSIDE The “More Growth in Europe” initiative includes 10 major infrastructure and 2 L’événement 10 Years of Eurocorps research projects designed to accelerate economic growth 3 France-Amérique 9/11 Commemorations RESIDENT links will be built between Profil JACQUES CHIRAC France's high speed TGV 4 and Chancellor Gerhard rail network and Studying in France Schroeder, accompanied Germany's ICE railways. 5 Économie Pby their foreign ministers and Another priority is to Vivendi and NBC other key cabinet members, develop sophisticated gathered on September 18 at the computer applications for 6 Société Berlin chancellery for the 81st air, rail, maritime and Cracking Down on Franco-German Summit. These road transportation. Last Teen Smoking talks are part of a planned series but not least, More 7 Culture of joint cabinet meetings agreed Growth in Europe 9/11 in French earlier this year to seal forty years includes three environ- Literature of Franco-German reconcilia- mental projects: increas- tion. The summit concluded ing the use of wind ener- 8 Chez nous with the adoption of a common gy, promoting the use of Triumph of The French and German cabinet members headed initiative, More Growth in alternative fuels and by President Chirac and Chancellor Schroeder. French Painting Europe, which lays the ground- zero-emission vehicles, (Berlin Chancellery, September 18) work for ten research and infra- and encouraging joint structure projects. -

— Zürich DL: Half the Diamonds Awarded —
Volume 9, No. 52 August 21, 2010 — Zürich DL: Half The Diamonds Awarded — by Ed Gordon headed into the final straight. The normally In the hurdles, David Oliver continued For sheer drama in the outcomes of the passive Wariner gave a rare emotional glimpse his unbeaten (12 in a row) season with a various Diamond races, the Zürich Welt- of his inner feelings with a crisp hand clap spectacular 12.93 after a lunge at the finish klasse final fell a bit short, as all 16 pre-meet after seeing the infield clock right after the brought him under the eyebeam. leaders survived to win their respective event’s finish as Gonzales followed in 44.51. Ryan Wilson, on Oliver’s immediate top prize. (The remaining 16 right, ran a strong first half, will be awarded at the Van but Dwight Thomas came Damme meeting in Brussels up at the end to claim 2nd on Friday.) from the American, 13.25– Within those encounters, 13.26. however, came some of the Veronica Campbell- riveting matchups that the Brown’s good start in the Zürich crowd has come to women’s 100 was almost expect in this fixture’s long (but not quite) negated in history. the final meters by Carmeli- Five of the 16 Dia- ta Jeter’s late burst. monds—the men’s 200, 400, Both were timed in 110H; women’s 100 & 1500) 10.89, with the Jamaican had been decided mathemat- getting the nod from the ically during the summer’s photo judge. It was not first 14 competitions, with enough to overcome Jeter’s the frontrunners merely hav- secure event advantage in ing to show up. -

(5.1.2009) - Edita: Real Federación Española De Atletismo
(1) Enero/January (5.1.2009) - Edita: Real Federación Española de Atletismo LV CROSS INTERNACIONAL ZORNOTZA Amorebieta (Vizcaya), 4 de enero HOMBRES Sénior-Promesa (10.700m): 1. Samuel Tsegay ERI 31:36 - 2. Moses Masai KEN 31:57 - 3. Kidane Tadesse ERI 32:02 - 4. Yonas Kifle ERI 32:14 - 5. Ayad lamdassem 32:17 - 6. Alemayehu Bezabeh 32:22 - 7. Javier Guerra 32:27 - 8. Cuthbert Nyasango ZIM 33:00 - 9. José Rios 33:10 - 10. Eliseo Martín 33:15 - 11. Jonay González 33:34 - 12. Pedro Nimo 33:35 - 13. Javier Crespo 33.35 - 14. Iván Fernández 33:36 - 15. Youness Ait-Adi MAR 33:39 - 16. Sergio Sánchez 33:46 - 17. Wilson Busienei UGA 33:54 - 18. Jesús de la Fuente 33:54 - 19. Fernando Rey 34:12 - 20. Moktar Benhari FRA 34:15 - 21. Driss Bensaid MAR 34.18 - 22. El Miloudi Dahbi MAR 34:54 - 23. Aimad Bouziane MAR 34.59 - 24. Kamel Ziani 35:04 - 25. Iván Hierro 35:12 - 26. Mohamed El Gouarrah MAR 35:15 - 27. Miguel Ángel Gamonal 35:31 - 28. Unai Sáenz 35:35 - 29. Juan Antonio Pousa 36:02 - 30. Pedro maría Muñoz 36:04 - 31. Julio Rey36.08 Júnior (6.700m): 1. Abdelacid Merzougui 22:52 - 2. Aitor Fernández 23:14 - 3. Jonathan Viego 23:26 Juvenil (6.700m): 1.Soufyane Safet 23:41 - 2. Fernando Ruiz 23:53 - 3. Diego Menéndez 24:19 Cadete (3.550m): 1. Dario Estrada 12:55 - 2. Beñat Etxabe 13:14 - 3. Ander Santos 13:41 Infantil (2.400m): 1. Mikel Fernández 9:04 - 2. -

Campionati Italiani Lancio Del Martello
CAMPIONATI ITALIANI LANCIO DEL MARTELLO Tratto dall’ Almanacco del lancio del martello di Gian Mario Castaldie aggiornato al 31-12-2016 I campionati italiani assoluti si sono svolti dal 1898 per gli uomini e dal 1923 per le donne, ma per quanto riguarda il lancio del martello si è cominciato a gareggiare rispettivamente nel 1920 (diciannovesima edizione) e nel 1995 (sessantaseiesima). Per la categoria promesse ci fu un “primo lancio”, vale a dire le edizioni del 1990 e 1991 (riservate agli atleti di 20 e 21 anni e che per il martello riguardarono solo gli uomini) mentre nel quadriennio successivo si svolse solo un criterium promesse. Poi i campionati italiani promesse ripresero nel 1996, anno in cui si disputò per la prima volta anche la gara femminile del martello. Per quanto riguarda gli juniores il lancio del martello fu presente per gli uomini già nella prima edizione del 1958, mentre per le donne il primo titolo italiano di specialità fu aggiudicato nel 1995. Per la categoria allievi il martello fu invece presente dal 1966 e per le allieve dal 1995, come per le juniores. Per la categoria cadetti venne disputata un’ unica edizione dei campionati nel 1983, che ovviamente riguardò soltanto i maschi e successivamente presero ad organizzarsi i criteria per regioni (individuali e/o a squadre) e soltanto nel 2004 i cadetti e le cadette ebbero il loro campionato italiano individuale. Il settore dei lanci cosiddetti “lunghi”, vale a dire disco, martello e giavellotto assegna anche il titolo di campione italiano invernale, mentre nel lancio del peso ci sono i campionati italiani indoor dal 1970. -

Hammer Throw 7,26Kg Men (IAAF Hammer Challenge)
RESULT LIST Hammer Throw 7,26kg Men (IAAF Hammer Challenge) RESULT NAME COUNTRY DATE VENUE WL 82.40 Pawel Fajdek POL 13 Jun 2017 Turku (Paavo Nurmi) MR 80.90 Sergej Litvinov 1990 TEMPERATURE HUMIDITY START TIME 15:05 19.5°C 52.1% June 17 2017 END TIME 15:59 18.5°C 55.6% PLACE BIB NAME COUNTRY DATE of BIRTH ORDER RESULT POINTS 1 2 3 4 5 6 1 Pawel Fajdek POL 4 Jun 89 8 78.67 76.90 78.67 75.48 X X X 2 Wojciech Nowicki POL 22 Feb 89 7 76.04 72.09 73.96 73.11 76.04 X X 3 Marcel Lomnický SVK 6 Jul 87 5 74.86 72.62 73.69 74.86 73.95 X X 4 Ashraf Amjad Al-Saifi QAT 20 Feb 95 2 73.84 70.28 72.15 73.84 72.19 72.85 X 5 Nick Miller GBR 1 May 93 4 73.74 73.74 X X X 72.31 X 6 Marco Lingua ITA 4 Jun 78 3 72.73 72.39 X X 72.41 X 72.73 7 Krisztián Pars HUN 18 Feb 82 6 72.67 72.15 72.67 X 71.32 72.37 X 8 Libor Charfreitag SVK 11 Sep 77 1 67.11 X 67.11 66.84 66.24 - - Pawel Fajdek won by 2.63m ALL-TIME TOP LIST 2017 TOP LIST RESULT NAME VENUE DATE RESULT NAME VENUE DATE 86.74 Yuriy Sedykh (URS) Stuttgart 30 Aug 1986 82.40 Pawel Fajdek (POL) Turku (Paavo Nurmi) 13 Jun 86.04 Sergey Litvinov (URS) Dresden 3 Jul 1986 78.54 Wojciech Nowicki (POL) Kielce 13 May 84.90 Vadim Devyatovskiy (BLR) Minsk 21 Jul 2005 78.04 Pavel Bareisha (BLR) Doha (Hamad Bin 6 May 84.86 Koji Murofushi (JPN) Praha (Stadion 29 Jun 2003 78.00 Esref Apak (TUR) Ankara 6 Jun 84.62 Igor Astapkovich (BLR) Sevilla 6 Jun 1992 77.92 Marcel Lomnický (SVK) Coral Gables, FL 7 Apr 84.51 Ivan Tsikhan (BLR) Grodno 9 Jul 2008 77.72 Mihaíl Anastasákis (GRE) Nikíti 11 Jun 84.48 Igor Nikulin (URS) Lausanne 12 Jul 1990 77.70 Serghei Marghiev (MDA) Chisinau 26 May 84.40 Jüri Tamm (URS) Banská Bystrica 9 Sep 1984 77.51 Nick Miller (GBR) Salinas (Hartnell), CA 21 Apr 84.19 Adrián Annus (HUN) Szombathely 10 Aug 2003 77.30 Quentin Bigot (FRA) Forbach (Schlossberg) 28 May 83.93 Pawel Fajdek (POL) Szczecin (Miejski 9 Aug 2015 77.23 Marco Lingua (ITA) Torino 7 May LEGEND WL World Lead MR Meeting Record Timing & Data service by OnlineSystem s.r.o. -

Asian Games: Haroun and Elseify Clinch Gold; Ogunode Bags Silver ARMSTRONG VAS Hamad Al Thani
SPORT Monday 27 August 2018 PAGE | 18 PAGE | 19 US Open: Djokovic Ferreira wants Al eyes title as ‘Big Four’ Sadd’s ‘best’ in first reunited leg Asian Games: Haroun and Elseify clinch gold; Ogunode bags silver ARMSTRONG VAS Hamad Al Thani. “I would like to won the silver medal in men’s THE PENINSULA dedicate this medal to our Amir, 100m. On Saturday, Faris Has- the Qatar Olympic Committee, souna won the silver medal men’s DOHA: QATAR won two gold my Federation, my coach, and my 94 kg weightlifting while Hamad medals and one silver on a very team. My next championship will Al Marri captured the bronze busy day at the 2018 Asian Games be the Word Continental Cham- medal in the double trap in Jakarta yesterday. pionship and I have to add competition. Abdalelah Haroun Hassan another medal and make my Qatar now have won two started the gold gush by clinching people and Qatar proud.” gold, two silver and one bronze. the top spot in the 400 metres in Elseify was delighted to China’s Su Bingtian was 44.89 seconds, while Ashraf clinch the gold medal. crowned Asia’s fastest man yes- Elseify won Qatar its second gold “Gold medal! Thank God, I terday, justifying the hype sur- medal in the Men’s Hammer can’t describe how happy I am. I rounding him by winning the blue Throw despatching the hammer was able to get this achievement riband 100 metres sprint gold in throw to a distance of 76.88 only after hard work and per- an Asian Games record time. -

RESULTS Hammer Throw Men
Split (CRO) IAAF/VTB Bank Continental Cup 4 - 5 September 2010 RESULTS Hammer Throw Men 04 SEP 2010 - 17:00 RESULT NAME AGE VENUE DATE World Record 86.74 Yuriy SEDYKH (URS) 31 Stuttgart 30 Aug 86 Championship Record 82.68 Tibor GÉCSEK (HUN) 34 Johannesburg 12 Sep 98 World Leading 80.99 Koji MUROFUSHI (JPN) 36 Rieti 28 Aug 10 START TIME 17:00 TEMPERATURE 26°C HUMIDITY 40% END TIME 17:41 TEMPERATURE 26°C HUMIDITY 40% PLACE BIB NAME TEAM COUNTRY DATE OF BIRTH ORDER RESULT 1 2 3 4 PTS 1 841 Libor CHARFREITAG EUR SVK 11 SEP 77 8 79.69 77.76 76.31 79.69 X 8 2 740 Dilshod NAZAROV APA TJK 6 MAY 82 2 78.76 76.22 78.08 76.99 78.76 7 3 735 Ali Mohamed AL-ZINKAWI APA KUW 27 FEB 84 6 76.73 X 74.16 74.72 76.73 6 4 830 Nicola VIZZONI EUR ITA 4 NOV 73 4 75.94 75.32 75.94 X 75.80 5 5 611 Roberto JANET AME CUB 29 AUG 86 7 74.87 74.06 74.87 72.54 X 4 6 628 A.G. KRUGER AME USA 18 FEB 79 3 74.00 X 74.00 X X 3 7 530 Chris HARMSE AFR RSA 31 MAY 73 1 71.06 X X 71.06 X 2 8 509 Mohsen EL ANANY AFR EGY 21 MAY 85 5 69.77 69.17 67.65 69.77 69.37 1 TEAM STANDINGS AFTER 2 OF 40 EVENTS 1 EUR Europe 24 2 AME Americas 20 3 APA Asia-Pacific 16 4 AFR Africa 12 ALL-TIME TOP LIST SEASON TOP LIST 86.74 Yuriy SEDYKH (URS) Stuttgart 30 Aug 86 80.99 Koji MUROFUSHI (JPN) Rieti 28 Aug 10 86.73 Ivan TSIKHAN (BLR) Brest, BLR 3 Jul 05 80.59 Libor CHARFREITAG (SVK) Walnut, CA 17 Apr 10 86.04 Sergey LITVINOV (RUS) Dresden 3 Jul 86 80.44 Pavel KRYVITSKI (BLR) Brest, BLR 22 May 10 84.90 Vadim DEVYATOVSKIY (BLR) Minsk 21 Jul 05 80.11 Dilshod NAZAROV (TJK) Dushanbe 18 Jun 10 84.86 Koji -

2013 World Championships Statistics – Men's HT
2013 World Championships Statistics – Men’s HT by K Ken Nakamura The records to look for in Moskva: 1) Krisztian Pars can be the first World Youth Champion to win the World Championships All time Performance List at the World Championships Performance Performer Distance Name Nat Pos Venue Year 1 1 83.89 Ivan Tikhon BLR 1 Helsinki 2005 2 83.63 Ivan Tikhon 1 Osaka 2007 3 2 83.38 Szymon Ziolkowski POL 1 Edmonton 2001 4 3 83.06 Sergey Litvinov URS 1 Roma 1987 5 83.05 Ivan Tikhon 1 Paris 2003 6 4 82.92 Koji Murofushi JPN 2 Edmonton 2001 7 82.68 Sergey Litvinov 1 Helsinki 1983 8 5 82.60 Vadim Devyatovski BLR 2 Helsinki 2005 9 6 82.29 Primoz Kozmus SLO 2 Osaka 2007 10 81.85 Szymon Ziolkowski 1qA Edmonton 2001 11 81.78 Sergey Litvinov 1qA Roma 1987 11 7 81.78 Heinz Weis GER 1 Athinai 1997 13 8 81.70 Yuriy Sedykh URS 1 Tokyo 1991 14 9 81.64 Andrey Abduvaliyev TJK 1 Stuttgart 1993 15 10 81.60 Libor Charfreitag SVK 3 Osaka 2007 16 81.57 Vadim Devyatovskiy BLR 4 Osaka 2007 17 81.56 Andrey Abduvaliyev 1 Göteborg 1995 18 11 81.46 Andrey Skvaruk UKR 2 Athinai 1997 19 81.24 Koji Murofushi 1 Daegu 2011 20 81.20 Vadim Devyatovski 1qA Helsinki 2005 21 12 81.18 Krisztian Pars HUN 2 Daegu 2011 22 13 81.10 Igor Astapkovich BLR 2 Göteborg 1995 22 14 80.98 Tibor Gecsek HUN 3 Göteborg 1995 24 80.94 Yuriy Sedykh 2 Helsinki 1983 24 80.94 Igor Astapkovich 2 Tokyo 1991 25 80.93 Krisztian Pars 5 Osaka 2007 27 15 80.84 Jüri Tamm URS 2 Roma 1987 27 80.84 Primoz Kozmus 1 Berlin 2009 29 16 80.76 Ralph Haber GDR 3 Roma 1987 29 16 80.76 Vasiliy Sidorenko RUS 3 Athiani 1997