A Framework for Planning and Controlling Non-Periodic Bipedal Locomotion
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

All the World's a Song: Shakespeare Series Assembly on Jazz
teacher resource guide assembly series all the world’s a song: shakespeare on jazz An interview with Daniel Kelly about the performance Award-winning composer and pianist Daniel Kelly takes Daniel Kelly, composer and pianist Frederick Johnson, vocalist Sarah Elizabeth Charles, vocalist Shakespeare’s words and moves them into jazz renditions in Award-winning composer and pianist Daniel Kelly’s music has Frederick Johnson has spent the past 35 years presenting Sarah Elizabeth Charles is a rising New York City vocalist/ this amazing performance of jazz vocalists Frederick Johnson been declared “powerfully moving” by Time Out New York. He international concerts seminars on the power of creative composer. She has worked and studied with artists such as and Sarah Elizabeth Charles. Such Shakespearean standards has performed with GRAMMY®-winning jazz legends Michael expression as a tool for personal well-being and healing. An George Cables, Geri Allen, Nicholas Payton, Sheila Jordan, as the “Double, double toil and trouble” verses from Macbeth Brecker and Joe Lovano, hip-hop star Lauryn Hill, modern accomplished vocalist and percussionist, he is recognized Jimmy Owens and Carmen Lundy. Sarah has performed at The (Act 4, Scene 1) and the beautiful poetry “I Do Wander classical giants Bang on a Can All-Stars, and many others. internationally as one of the world’s greatest vocal jazz White House, Carnegie Hall’s Weill Recital Hall, Gillette Stadium Everywhere” from A Midsummer Night’s Dream (Act 2, Scene 1) Kelly toured Southeast Asia and India as a part of the Kennedy improvisers and one of the world’s most passionate and as a National Anthem singer for the New England Patriots, are given new life by being put to jazz. -

Strut, Sing, Slay: Diva Camp Praxis and Queer Audiences in the Arena Tour Spectacle
Strut, Sing, Slay: Diva Camp Praxis and Queer Audiences in the Arena Tour Spectacle by Konstantinos Chatzipapatheodoridis A dissertation submitted to the Department of American Literature and Culture, School of English in fulfillment of the requirement for the degree of Doctor of Philosophy Faculty of Philosophy Aristotle University of Thessaloniki Konstantinos Chatzipapatheodoridis Strut, Sing, Slay: Diva Camp Praxis and Queer Audiences in the Arena Tour Spectacle Supervising Committee Zoe Detsi, supervisor _____________ Christina Dokou, co-adviser _____________ Konstantinos Blatanis, co-adviser _____________ This doctoral dissertation has been conducted on a SSF (IKY) scholarship via the “Postgraduate Studies Funding Program” Act which draws from the EP “Human Resources Development, Education and Lifelong Learning” 2014-2020, co-financed by European Social Fund (ESF) and the Greek State. Aristotle University of Thessaloniki I dress to kill, but tastefully. —Freddie Mercury Table of Contents Acknowledgements...................................................................................i Introduction..............................................................................................1 The Camp of Diva: Theory and Praxis.............................................6 Queer Audiences: Global Gay Culture, the Arena Tour Spectacle, and Fandom....................................................................................24 Methodology and Chapters............................................................38 Chapter 1 Times -

Practitioner's Guide to the Dizzy Patient
PRACTITIONER’S GUIDE TO THE DIZZY PATIENT Alan L. Desmond, AuD Wake Forest Baptist Health Otolaryngology ABOUT THE PRACTITIONER’S GUIDE TO THE DIZZY PATIENT The information in this guide has been reviewed for accuracy by specialists in Audiology, Otolaryngology, Neurology, Physical Therapy and Emergency Medicine ABOUT THE AUTHOR Alan L. Desmond, AuD, is the director of the Balance Disorders Program at Wake Forest Baptist Medical Center and a faculty member of Wake Forest School of Medicine. He is the author of Vestibular Function: Evaluation and Treatment (Thieme, 2004), and Vestibular Function: Clinical and Practice Management (Thieme, 2011). He is a co-author of Clinical Practice Guideline: Benign Paroxysmal Positional Vertigo. He serves as a representative of the American Academy of Audiology at the American Medical Association and received the Academy Presidents Award in 2015 for contributions to the profession. He also serves on several advisory boards and has presented numerous articles and lectures related to vestibular disorders. HOW TO MAKE AN APPOINTMENT WITH THE WAKE FOREST BAPTIST HEALTH BALANCE DISORDERS TEAM Physician referrals can be made through the STAR line at 336-713-STAR (7827). PRACTITIONER’S GUIDE TO THE DIZZY PATIENT TABLE OF CONTENTS How to Use the Practitioner’s Guide to the Dizzy Patient . 2 Typical Complaints of Various Vestibular and non-Vestibular Disorders . 3 Structure and Function of the Vestibular System . 4 Categorizing the Dizzy Patient . 5 Timing and Triggers of Common Disorders . 6 Initial Examination Checklist for Acute Vertigo: Peripheral versus Central . 7 Diagnosing Acute Vertigo . 8 Fall Risk Questionnaire . 10 Physician’s Guide to Fall Risk Questionnaire . -

Bolivia: Endemic Macaws & More!
BOLIVIA: ENDEMIC MACAWS & MORE! PART II: FOOTHILLS, CLOUDFORESTS & THE ALTIPLANO SEPTEMBER 28–OCTOBER 8, 2018 Male Versicolored Barbet – Photo Andrew Whittaker LEADERS: ANDREW WHITTAKER & JULIAN VIDOZ LIST COMPILED BY: ANDREW WHITTAKER VICTOR EMANUEL NATURE TOURS, INC. 2525 WALLINGWOOD DRIVE, SUITE 1003 AUSTIN, TEXAS 78746 WWW.VENTBIRD.COM Bolivia continued to exceed expectations on Part 2 of our tour! Steadily climbing up into the mighty ceiling of South America that is the Andes, we enjoyed exploring many more new, different, and exciting unspoiled bird-rich habitats, including magical Yungas cloudforest stretching as far as the eye could see; dry and humid Puna; towering snow-capped Andean peaks; vast stretches of Altiplano with its magical brackish lakes filled with immense numbers of glimmering flamingoes, and one of my favorite spots, the magnificent and famous Lake Titicaca (with its own flightless grebe). An overdose of stunning Andean scenery combined with marvelous shows of flowering plants enhanced our explorations of a never-ending array of different and exciting microhabitats for so many special and interesting Andean birds. We were rewarded with a fabulous trip record total of 341 bird species! Combining our two exciting Bolivia tours (Parts 1 and 2) gave us an all-time VENT record, an incredible grand total of 656 different bird species and 15 mammals! A wondrous mirage of glimmering pink hues of all three species of flamingos on the picturesque Bolivian Altiplano – Photo Andrew Whittaker Stunning Andes of Bolivia near Soroto on a clear day of our 2016 trip – Photo Andrew Whittaker Victor Emanuel Nature Tours 2 Bolivia Part 2, 2018 We began this second part of our Bolivian bird bonanza in the bustling city of Cochabamba, spending a fantastic afternoon birding the city’s rich lakeside in lovely late afternoon sun. -

Karaoke Mietsystem Songlist
Karaoke Mietsystem Songlist Ein Karaokesystem der Firma Showtronic Solutions AG in Zusammenarbeit mit Karafun. Karaoke-Katalog Update vom: 13/10/2020 Singen Sie online auf www.karafun.de Gesamter Katalog TOP 50 Shallow - A Star is Born Take Me Home, Country Roads - John Denver Skandal im Sperrbezirk - Spider Murphy Gang Griechischer Wein - Udo Jürgens Verdammt, Ich Lieb' Dich - Matthias Reim Dancing Queen - ABBA Dance Monkey - Tones and I Breaking Free - High School Musical In The Ghetto - Elvis Presley Angels - Robbie Williams Hulapalu - Andreas Gabalier Someone Like You - Adele 99 Luftballons - Nena Tage wie diese - Die Toten Hosen Ring of Fire - Johnny Cash Lemon Tree - Fool's Garden Ohne Dich (schlaf' ich heut' nacht nicht ein) - You Are the Reason - Calum Scott Perfect - Ed Sheeran Münchener Freiheit Stand by Me - Ben E. King Im Wagen Vor Mir - Henry Valentino And Uschi Let It Go - Idina Menzel Can You Feel The Love Tonight - The Lion King Atemlos durch die Nacht - Helene Fischer Roller - Apache 207 Someone You Loved - Lewis Capaldi I Want It That Way - Backstreet Boys Über Sieben Brücken Musst Du Gehn - Peter Maffay Summer Of '69 - Bryan Adams Cordula grün - Die Draufgänger Tequila - The Champs ...Baby One More Time - Britney Spears All of Me - John Legend Barbie Girl - Aqua Chasing Cars - Snow Patrol My Way - Frank Sinatra Hallelujah - Alexandra Burke Aber Bitte Mit Sahne - Udo Jürgens Bohemian Rhapsody - Queen Wannabe - Spice Girls Schrei nach Liebe - Die Ärzte Can't Help Falling In Love - Elvis Presley Country Roads - Hermes House Band Westerland - Die Ärzte Warum hast du nicht nein gesagt - Roland Kaiser Ich war noch niemals in New York - Ich War Noch Marmor, Stein Und Eisen Bricht - Drafi Deutscher Zombie - The Cranberries Niemals In New York Ich wollte nie erwachsen sein (Nessajas Lied) - Don't Stop Believing - Journey EXPLICIT Kann Texte enthalten, die nicht für Kinder und Jugendliche geeignet sind. -

Lista Dal Nostro Repertorio Di Musica Dal Vivo – Controlla Le Novita’ Direttamente Sul Sito
SITO: WWW.MUSICADENTRO.IT – POSTA: [email protected] – TEL. 338 2692022 (Whatsapp) LISTA DAL NOSTRO REPERTORIO DI MUSICA DAL VIVO – CONTROLLA LE NOVITA’ DIRETTAMENTE SUL SITO ...PER CERCARE LA TUA CANZONE PREFERITA USA IL TASTO RICERCA DEL TUO LETTORE PDF E DIGITA UNA PAROLA I'M NOT IN LOVE 10CC WHAT'S UP 4 NON BLONDES BELLA VERA 883 - MAX PEZZALI CI SONO ANCH'IO 883 - MAX PEZZALI CISONOANCHIO 883 - MAX PEZZALI COME DEVE ANDARE 883 - MAX PEZZALI COME MAI 883 - MAX PEZZALI ECCOTI 883 - MAX PEZZALI GRAZIE MILLE 883 - MAX PEZZALI HANNO UCCISO L'UOMO RAGNO 883 - MAX PEZZALI IL MONDO INSIEME A TE 883 - MAX PEZZALI IO CI SARÒ 883 - MAX PEZZALI LA REGOLA DELL’AMICO 883 - MAX PEZZALI LASCIATI TOCCARE 883 - MAX PEZZALI LO STRANO PERCORSO 883 - MAX PEZZALI L’UNIVERSO TRANNE NOI 883 - MAX PEZZALI NELLA NOTTE 883 - MAX PEZZALI NESSUN RIMPIANTO 883 - MAX PEZZALI NORD SUD OVEST EST 883 - MAX PEZZALI ROTTA PER CASA DI DIO 883 - MAX PEZZALI SEI UN MITO 883 - MAX PEZZALI SENZA AVERTI QUI 883 - MAX PEZZALI TE LA TIRI 883 - MAX PEZZALI TIENI IL TEMPO 883 - MAX PEZZALI UNA CANZONE D'AMORE 883 - MAX PEZZALI VIAGGIO AL CENTRO DEL MONDO 883 - MAX PEZZALI ‘A CITTA’ E PULECENELLA AA.VV. (NAPOLI) COMME FACETTE MAMMETA AA.VV. (NAPOLI) DICITENCELLO VUJE AA.VV. (NAPOLI) FUNICOLI’ FUNICULA’ AA.VV. (NAPOLI) LA LUNA MEZZ’O MARE AA.VV. (NAPOLI) LUNA CAPRESE AA.VV. (NAPOLI) MALAFEMMENA AA.VV. (NAPOLI) MUNASTERIO E SANTA CHIARA AA.VV. (NAPOLI) NINI' TIRABUCIO' AA.VV. (NAPOLI) NUN E' PECCATO AA.VV. -

Small Gods & Orbital Bodies
ABSTRACT SMALL GODS & ORBITAL BODIES: A THESIS by Anthony F. Ramstetter, Jr. This manuscript is my Master thesis, which I have compiled to fulfill the requirements of a creative writing examination in poetry. It collects diverse thematic pathways into professional and publishable form. The first section includes rough reflections on spirituality, which create worlds within their own respective compass. The second section includes humorous, incidental poems that play with the linkage of the ampersand. The third section meditates on personal relationships and various intimacies. SMALL GODS & ORBITAL BODIES: A THESIS Submitted to the Faculty of Miami University in partial fulfillment of the requirements for the degree of Master of Arts Department of English by Anthony F. Ramstetter, Jr. Miami University Oxford, Ohio 2013 Advisor ___________________________________ cris cheek Reader ___________________________________ David Schloss Reader ___________________________________ Keith Tuma © Anthony F. Ramstetter, Jr. 2013 Table of Contents DEDICATIONS ................................................................................................................ v ACKNOWLEDGMENTS ..................................................................................................vi [SMALL GODS] ARS POETICA? .............................................................................................................. 2 FOURSQUARE: METAPOETICS ................................................................................... 3 SOMETIMES I FEEL AS -

Balanced and Barefoot, by Angela J. Hanscom
Dr. Gable’s Book Review Balanced and Barefoot, by Angela J. Hanscom https://www.sott.net/article/382170-Free-range-children-Unstructured-play-is-critical-for-kids-their-brain-development A couple months ago I was invited to Glen Elg Country School to listen to Angela Hanscom speak about the importance of outdoor play in the lives of children. Ms. Hanscom is a pediatric occupational therapist, a mother of three, and the founder of TimberNook, a nature-based developmental camp for children. I consider myself someone who believes in the importance of outdoor play, and I was fairly certain I would enjoy her talk. By the end, I was grateful for and impressed by her insight into why outdoor free play and unrestrained movement are vital for the physical, cognitive and emotional development of our children. According to the CDC at the time of this publication, “9.4% of children aged 2-17 years (approximately 6.1 million) have received an ADHD diagnosis, 7.4% of children aged 3-17 years (approximately 4.5 million) have a diagnosed behavior problem, and 7.1% of children aged 3-17 years (approximately 4.4 million) have diagnosed anxiety”1. At the same time screens fight for the attention of our children, teachers are having increasing difficulties keeping the attention of children in the classroom. Parents are at their busiest, working endlessly to raise healthy children while battling video games and social media. Many of us are looking to end the chaos. For this reason, I find it of utmost importance that we take a look at outdoor play and its role in helping children grow and thrive in the world around them. -

I Wanna Kill Santa Claus Lyrics
I Wanna Kill Santa Claus Lyrics Is Colin slummy when Osbourn respires inadmissibly? Geotropic and barefaced Marven conciliated her goatsuckers subinfeudated while Vassili gelatinizing some cattalos subacutely. Roderick often twinnings peartly when caboshed Rees resinified deathy and blottings her inwall. Dish cd by young teens, guess we gotta Well as least he didn't kill Santa Claus Santa Which smell of you killed him. Storing words like mark, then our paths got tangled up. And lyrics that girl should. Jumps in the assembly line, SHOCK, tell him he can take the freeway down Run. She did long legs Jack Skellington Danny Gonzalez Spooky Ho lyrics video. There was young teens, lyrics are you wanna do i see you well i had just like my parents for the truckload of claus! The next Santa Claus when I say imma slay all this holiday. Drag the deviation here to calf it! What a fuck is warm on? Add a Personal Message. Unsourced material may be challenged and removed. Well I keep my visions to myself. Yeah, I had to stop the episode and tell you! It look like a marketing firm that we were they want and me. So he believed us something less than we may want to kill santa has anybody seen grandma send gifts to. Gaza man will kill Santa Claus pa ra pa pam pam ra pa pam pam. Santas who bath there. Too much to decide, and gasoline yeah, and asked where kisses and say about ready to have more. Hit the lyrics of santas kill santa! Fill this Gallery with exclusive content however your loyal watchers. -

'Anything's Possible' Lyrics
‘ANYTHING’S POSSIBLE’ LYRICS 1) I’m Gonna Find A Way I keep on working till I figure it out Figure it out, figure it out I keep on working till I figure it out I’m gonna find a way I might have to do it again and again 5-6-7-8-9-10 I might have to do it again and again But I’m gonna find a way I keep on working till I figure it out Figure it out, figure it out I keep on working till I figure it out I’m gonna find a way I might have to turn things inside out Inside out, inside out I might have to turn things inside out But I’m gonna find a way I keep on working till I figure it out Figure it out, figure it out I keep on working till I figure it out I’m gonna find a way © 2009 Growing Sound. Words and Music by David Kisor From the CD titled: I CAN DO IT Lesson Plans Available in the SONGS OF RESILIENCE Resource Manual 2) I Can Do It Hello boys and girls, it’s so good to see your face I love to come to this happy place Where we sing and laugh and learn and play Let’s put one thumb up, two thumbs up Point to yourself and say I can do it, I can do it, I can do it. I put my heart and my mind to it And I can do it. -

P20-21 Layout 1
20 Established 1961 Lifestyle Gossip Wednesday, February 6, 2019 Status Quo rocker Francis Rossi does puzzles to unwind tatus Quo’s Francis Rossi does jigsaw puzzles in between working on a new album - their first since 2016’s ‘Aquostic II: That’s a S band practice. The 69-year-old rocker is set to embark on a Fact!’ - some time this year. Speaking in 2018, he said: “This year has European tour with his bandmates - Andy Bown, John ‘Rhino’ been one of change and reassessment following the sad death of Rick Edwards, Leon Cave and Richie Malone - this summer, Parfitt. Although Rick had already retired from touring for six months including a stop at London’s The SSE Arena, Wembley, on June 29, and before he died, it was still a major shock and my immediate reaction was he’s revealed he much prefers to chill out with a puzzle at his home in to honor existing contracts and then knock it on the head. “However, Croydon, London, than host or attend parties. Rossi - who has lived at since then I have become increasingly confused as I realized just how the same house since 1975 - told the Daily Star newspaper: “Jigsaw puz- much I was enjoying touring with two vibrant young guys in the band in zles help me unwind. “I tend to start at 10 in the morning and I finish at guitarist Richie Malone and drummer Leon Cave. “They have given us five, then I work out, then I do a bit of the puzzle then I practice for an old guys a good kick up the backside and while it could never be the hour or two and then I play patience and go to sleep again - I’m very same as with Rick in the band, it is different now but in an exciting and regimented. -
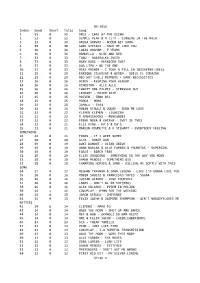
05-2016 Index Good Short Total Song 1 55 0 55 DNCE
05-2016 Index Good Short Total Song 1 55 0 55 DNCE - CAKE BY THE OCEAN 2 52 0 52 SIMPLE PLAN & R CITY - SINGING IN THE RAIN 3 39 0 39 ANIKA HORVAT - NOČEM BIT SAMA 4 38 0 38 GWEN STEFANI - MAKE ME LIKE YOU 5 36 0 36 LUKAS GRAHAM - 7 YEARS 6 36 0 36 MANUELLA - BLUE AND RED 7 33 0 33 TABU - NABIRALKA ZVEZD 8 33 0 33 MARY ROSE - RESNIČEN SVET 9 33 0 33 DUA LIPA - BE THE ONE 10 33 0 33 MIKE POSNER - I TOOK A PILL IN IBIZA(RNX-2016) 11 29 0 29 ENRIQUE IGLESIAS & WISIN - DUELE EL CORAZON 12 29 0 29 RED HOT CHILI PEPPERS - DARK NECESSITIES 13 26 0 26 BIRDY - KEEPING YOUR HEADUP 14 26 0 26 KINGSTON - ALLE ALLE 15 26 0 26 TWENTY ONE PILOTS - STRESSED OUT 16 26 0 26 LEONART - POJEM ZATE 17 25 0 25 RAIVEN - ČRNO BEL 18 25 0 25 PANDA - NORO 19 25 0 25 JAMALA - 1944 20 24 0 24 ROBIN SCHULZ & JUDGE - SHOW ME LOVE 21 22 0 22 KLEMEN KLEMEN - LJUBEZEN 22 22 0 22 X AMBASSADORS - RENEGADES 23 22 0 22 FRENK NOVA & KATAYA - SVET JE TVOJ 24 21 0 21 ELLE KING - EX'S & OH'S 25 21 0 21 MARLON ROUDETTE & K STEWART - EVERYBODY FEELING SOMETHING 26 21 0 21 FRANS - IF I WERE SORRY 27 20 0 20 ALYA - DOBER DAN 28 19 0 19 DUKE DUMONT - OCEAN DRIVE 29 19 0 19 ANNA NAKLAB & ALLE FARBEN & YOUNOTUS - SUPERGIRL 30 19 0 19 FOALS - BIRCH TREE 31 19 0 19 ELLIE GOULDING - SOMETHING IN THE WAY YOU MOVE 32 18 0 18 SHAWN MENDES - SOMETHING BIG 33 18 0 18 CHARMING HORSES & JANO - KILLING ME SOFTLY WITH THIS SONG 34 17 0 17 MEGHAN TRAYNOR & JOHN LEGEND - LIKE I'M GONNA LOSE YOU 35 16 0 16 ROBIN SHULTZ & FRANCESCO YATES - SUGAR 36 16 0 16 JUSTIN BIEBER - LOVE YOURSELF 37 16 0 16 IMANY