Rainfall Variability Analysis in the Nira River Basin Using Multi-Model Gcm Ensemble
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

District Taluka Center Name Contact Person Address Phone No Mobile No
District Taluka Center Name Contact Person Address Phone No Mobile No Mhosba Gate , Karjat Tal Karjat Dist AHMEDNAGAR KARJAT Vijay Computer Education Satish Sapkal 9421557122 9421557122 Ahmednagar 7285, URBAN BANK ROAD, AHMEDNAGAR NAGAR Anukul Computers Sunita Londhe 0241-2341070 9970415929 AHMEDNAGAR 414 001. Satyam Computer Behind Idea Offcie Miri AHMEDNAGAR SHEVGAON Satyam Computers Sandeep Jadhav 9881081075 9270967055 Road (College Road) Shevgaon Behind Khedkar Hospital, Pathardi AHMEDNAGAR PATHARDI Dot com computers Kishor Karad 02428-221101 9850351356 Pincode 414102 Gayatri computer OPP.SBI ,PARNER-SUPA ROAD,AT/POST- 02488-221177 AHMEDNAGAR PARNER Indrajit Deshmukh 9404042045 institute PARNER,TAL-PARNER, DIST-AHMEDNAGR /221277/9922007702 Shop no.8, Orange corner, college road AHMEDNAGAR SANGAMNER Dhananjay computer Swapnil Waghchaure Sangamner, Dist- 02425-220704 9850528920 Ahmednagar. Pin- 422605 Near S.T. Stand,4,First Floor Nagarpalika Shopping Center,New Nagar Road, 02425-226981/82 AHMEDNAGAR SANGAMNER Shubham Computers Yogesh Bhagwat 9822069547 Sangamner, Tal. Sangamner, Dist /7588025925 Ahmednagar Opposite OLD Nagarpalika AHMEDNAGAR KOPARGAON Cybernet Systems Shrikant Joshi 02423-222366 / 223566 9763715766 Building,Kopargaon – 423601 Near Bus Stand, Behind Hotel Prashant, AHMEDNAGAR AKOLE Media Infotech Sudhir Fargade 02424-222200 7387112323 Akole, Tal Akole Dist Ahmadnagar K V Road ,Near Anupam photo studio W 02422-226933 / AHMEDNAGAR SHRIRAMPUR Manik Computers Sachin SONI 9763715750 NO 6 ,Shrirampur 9850031828 HI-TECH Computer -

Solapur University, Solapur Solapur
Solapur University, Solapur http://su.digitaluniversity.ac Solapur-Pune National Highway, Kegaon, Solapur-413255, Maharashtra(India) Merit List B.Sc.-Regular-Credit System 2014(No Branch) for Mar-2017 Template Name: BSc CGPA NO Branch Sr. Merit Name of Student Gender CGPA Percentage Earned College Name PRN Seat No. No. Credits (Code) Number 1 1 KULKARNI VRUSHALI Female 6.00 97.79 152.00 Sangameshwa r 2014032500095887 364444 ABHIJEET College(SAN) Address FLAT NO 2 SINGI COMPLEX SOUTH SADAR BAZAR LASHKAR City : SOLAPUR Taluka : Solapur(s) Distict : Solapur State : Maharashtra Pin : 413003 Mobile Number : 919822520268 Email ID : Not Available 2 2 SHAIKH RESHMA ALLABAKSH Female 6.00 96.69 152.00 Shankarrao 2014032500162187 364268 Mohite Address Mahavidyalaya AP- AKLUJ (SMM) City : AKLUJ Taluka : Malshiras Distict : Solapur State : Maharashtra Pin : 413118 Mobile Number : 919423327776 Email ID : Not Available 3 3 HOUDE SRUSTI RAJENDRA Female 6.00 95.98 152.00 Sangameshwa r 2014032500095485 364434 College(SAN) Address 264 B OM NAM SHIVAY NAGAR HATTURE NAGER SOLAPUR City : SOLAPUR Taluka : Solapur(s) Distict : Solapur State : Maharashtra Pin : 413001 Mobile Number : 919881393352 Email ID : Not Available 4 4 PAWAR DIVYA Female 6.00 95.71 152.00 Shankarrao 2014032500162156 364263 CHANDRAKANT Mohite Address Mahavidyalaya AP- AKLUJ (SMM) City : AKLUJ Taluka : Malshiras Distict : Solapur State : Maharashtra Pin : 413118 Mobile Number : 919766901344 Email ID : Not Available Page 2 of 11 Solapur University, Solapur http://su.digitaluniversity.ac Solapur-Pune National Highway, Kegaon, Solapur-413255, Maharashtra(India) Merit List B.Sc.-Regular-Credit System 2014(No Branch) for Mar-2017 Template Name: BSc CGPA NO Branch Sr. -

6. Water Quality ------61 6.1 Surface Water Quality Observations ------61 6.2 Ground Water Quality Observations ------62 7
Version 2.0 Krishna Basin Preface Optimal management of water resources is the necessity of time in the wake of development and growing need of population of India. The National Water Policy of India (2002) recognizes that development and management of water resources need to be governed by national perspectives in order to develop and conserve the scarce water resources in an integrated and environmentally sound basis. The policy emphasizes the need for effective management of water resources by intensifying research efforts in use of remote sensing technology and developing an information system. In this reference a Memorandum of Understanding (MoU) was signed on December 3, 2008 between the Central Water Commission (CWC) and National Remote Sensing Centre (NRSC), Indian Space Research Organisation (ISRO) to execute the project “Generation of Database and Implementation of Web enabled Water resources Information System in the Country” short named as India-WRIS WebGIS. India-WRIS WebGIS has been developed and is in public domain since December 2010 (www.india- wris.nrsc.gov.in). It provides a ‘Single Window solution’ for all water resources data and information in a standardized national GIS framework and allow users to search, access, visualize, understand and analyze comprehensive and contextual water resources data and information for planning, development and Integrated Water Resources Management (IWRM). Basin is recognized as the ideal and practical unit of water resources management because it allows the holistic understanding of upstream-downstream hydrological interactions and solutions for management for all competing sectors of water demand. The practice of basin planning has developed due to the changing demands on river systems and the changing conditions of rivers by human interventions. -

Final ROUTE DETAILS
th 6 Edition - Route Details The Route The Race starts in Pune, the city of cycles, and finishes in Goa, on the sea shore. Set on the Deccan Plateau, the route follows the Sahyadri Range, which defines the western edge of the Deccan, finally dropping through dense forests that cover the cliffs of the Escarpment, into the Konkan as it heads to the Indian Ocean. Each year the route is modified to adjust to road conditions. This year the route goes via Surur phata through Wai to Panchagani, turning south to go through Bhilar towards Medha/Satara. From Satara till Belur (just before Dharwad it remains on the NH4, turning back to Belgaum to head for Goa through Chorla Ghat. Route Details have been finalized after a physical inspection of road conditions conducted by the team in end of October. We do not expect any further changes, except if there are any extenuating circumstances. If there are any last minute changes, participants will be notified. Description / Cautions The Start Venue for this edition is The Cliff Restaurant and Club, at Forest Trails Bhugaon, Paranjape Schemes (Construction) Ltd which has hosted the start of the last 2 editions. From there one heads steeply downhill and on to Chandni chowk to join NH4, heading south towards Bangalore. The first climb to Katraj tunnel is followed by a flat, slight downhill until one crosses the Nira River at Shirwal at @60 km. While this stretch usually offers an opportunity to do very good time, this year there are some sections under construction and participants are cautioned that the service roads that one has to take, are in bad condition. -
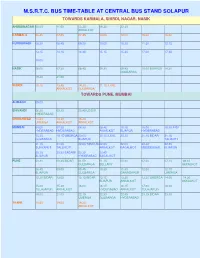
M.S.R.T.C. Bus Time-Table at Central Bus Stand Solapur
M.S.R.T.C. BUS TIME-TABLE AT CENTRAL BUS STAND SOLAPUR TOWARDS KARMALA, SHIRDI, NAGAR, NASIK AHMEDNAGAR 08.00 11.00 13.25 16.30 22.30 AKKALKOT KARMALA 06.45 07.00 07.45 10.00 12.00 15.30 16.00 KURDUWADI 08.30 08.45 09.20 10.00 10.30 11.30 12.15 13.15 14.15 14.45 15.15 15.30 17.00 17.45 18.00 NASIK 06.00 07.30 08.45 09.30 09.45 10.00 BIJAPUR 14.30 GULBARGA 19.30 21.00 SHIRDI 10.15 13.45 14.30 21.15 ILKAL AKKALKOT GULBARGA TOWARDS PUNE, MUMBAI ALIBAGH 09.00 BHIVANDI 06.30 09.30 20.45 UDGIR HYDERABAD CHINCHWAD 13.30 14.30 15.30 UMERGA AKKALKOT AKKALKOT MUMBAI 04.00 07.30 08.30 08.45 10.15 15.00 15.30 INDI HYDERABAD HYDERABAD AKKALKOT BIJAPUR HYDERABAD 15.30 19.15 UMERGA 20.00 20.15 ILKAL 20.30 21.15 BIDAR 21.15 GULBARGA BIJAPUR TALIKOTI 21.15 21.30 22.00 TANDUR 22.00 22.00 22.30 22.45 SURYAPET TALLIKOTI AKKALKOT BAGALKOT MUDDEBIHAL BIJAPUR 23.15 23.30 BADAMI 23.30 23.45 BIJAPUR HYDERABAD BAGALKOT PUNE 00.30 00.45 BIDAR 01.00 01.15 05.30 07.00 07.15 08.15 GULBARGA BELLARY AKKALKOT 08.45 09.00 09.45 10.30 11.30 12.00 12.15 BIJAPUR GULBARGA GANAGAPUR UMERGA 12.30 BIDAR 13.00 13.15 BIDAR 13.15 13.30 13.30 UMERGA 14.00 14.30 BIJAPUR AKKALKOT AKKALKOT 15.00 15.30 16.00 16.15 16.15 17.00 18.00 TULAJAPUR AKKALKOT HYDERABAD AKKALKOT TULAJAPUR 19.00 21.00 22.15 22.30 22.45 23.15 BIDAR 23.30 UMERGA GULBARGA HYDERABAD THANE 10.45 19.00 19.30 AKKALKOT TOWARDS AKKALKOT, GANAGAPUR, GULBARGA AKKALKOT 04.15 05.45 06.00 08.15 09.15 09.15 10.30 10.45 11.00 11.30 11.45 12.15 13.45 14.15 15.30 16.00 16.30 16.45 17.00 GULBARGA 02.00 PUNE 05.15 06.15 07.30 08.15 -

GOVT. of MAHARASHTRA Public Works Division, Akluj - 413 101 Phone No
7 GOVT. OF MAHARASHTRA Public Works Division, Akluj - 413 101 Phone No. 02185/227490 Web-www.mahapwd.com & [email protected] E-TENDER NOTICE NO . 07 FOR 2016-2017 Sealed online B-1 e - tenders for the following work are invited by the Executive Engineer, Public Works Division, Akluj-413 101(Telephone No.02185/227490) from the contractors Registered with Government of Maharashtra Public Work Department in appropriate class e-tender Estimated Earnest Time limit for Cost of e -tender Class of Name of Work work No. Cost Rs. Money Rs. Completion Form Fee Rs. Contractor Improvements to 1,000/- 21,800/- Yashawantnagar 6 Month (Non- Refundable) via E-Payment Class V A 1 kukuttpalan to MDR 91 to 21,75,314/- including via E-Payment Gateway mode and Above V.R. 195 km 0/00 to 1/00 tal- Manson Gateway mode Online only Malshiras, Dist-Solapur. Online only Improvements to Velapur 1,000/- 13,100/- Chavanwadi To Akluj - 6 Month (Non- Refundable) via E-Payment Class V A 2 Sangola Road V.R.213 Km 13,04,434/- including via E-Payment Gateway mode and Above 0/00 to 1/00 Tal. Malshiras Manson Gateway mode Online only Dist. Solapur Online only Improvements to Piliv - 1,000/- 21,800/- Zanjeawsti Gaothan Road 6 Month (Non- Refundable) via E-Payment Class V A 3 O.D.R. 135 Km 0/00 to 1/00 21,77,366/- including via E-Payment Gateway mode and Above Tal. Malshiras Dist Solapur Manson Gateway mode Online only Online only Metalling & Black topping 1,000/- 21,800/- to S.H. -

Satara District Maharashtra
1798/DBR/2013 भारत सरकार जल संसाधन मंत्रालय कᴂ द्रीय भूजल बो셍ड GOVERNMENT OF INDIA MINISTRY OF WATER RESOURCES CENTRAL GROUND WATER BOARD महाराष्ट्र रा煍य के अंत셍डत सातारा जजले की भूजल विज्ञान जानकारी GROUND WATER INFORMATION SATARA DISTRICT MAHARASHTRA By 饍िारा Abhay Nivasarkar अभय ननिसरकर Scientist-B िैज्ञाननक - ख म鵍य क्षेत्र, ना셍पुर CENTRAL REGION, NAGPUR 2013 1 SATARA DISTRICT AT A GLANCE 1. LOCATION North latitude : 17°05’ to 18°11’ East longitude : 73°33’ to 74°54’ Normal Rainfall : 473 -6209 mm 2. GENERAL FEATURES Geographical area : 10480 sq.km. Administrative division : Talukas – 11 ; Satara , Mahabeleshwar (As on 31.3.2013) Wai, Khandala, Phaltan, Man,Jatav, Koregaon Jaoli, , Patan, Karad. Towns : 10 Villages : 1721 Watersheds : 52 3. POPULATION (2001, 2010 Census) : 28.09,000., 3003922 Male : 14.08,000, 1512524 Female : 14.01,000, 1491398 Population growth (1991-2001) : 14.59, 6.94 % Population density : 268 , 287 souls/sq.km. Literacy : 78.22 % Sex ratio : 995 (2010 Census) Normal annual rainfall : 473 mm 6209 mm (2001-2010) 4 GEOMORPHOLOGY Major Geomorphic Unit : Western Ghat, Foothill zone , Central , : Plateau and eastern plains Major Drainage : Krishna, Nira, Man 5 LAND USE (2010) Forest area : 1346 sq km Net Sown area : 6960 sq km Cultivable area : 7990 sq km 6 SOIL TYPE : 2 Medium black, Deep black 7 PRINCIPAL CROPS Jawar : 2101 sq km Bajara : 899 sq km Cereals : 942 sq km Oil seeds : 886 sq km Sugarcane : 470 sq km 8 GROUND WATERMONITORING Dugwell : 46 Piezometer : 06 9 GEOLOGY Recent : Alluvium i Upper-Cretaceous to -

District Survey Report 2020-2021
District Survey Report Satara District DISTRICT MINING OFFICER, SATARA Prepared in compliance with 1. MoEF & CC, G.O.I notification S.O. 141(E) dated 15.1.2016. 2. Sustainable Sand Mining Guidelines 2016. 3. MoEF & CC, G.O.I notification S.O. 3611(E) dated 25.07.2018. 4. Enforcement and Monitoring Guidelines for Sand Mining 2020. 1 | P a g e Contents Part I: District Survey Report for Sand Mining or River Bed Mining ............................................................. 7 1. Introduction ............................................................................................................................................ 7 3. The list of Mining lease in District with location, area, and period of validity ................................... 10 4. Details of Royalty or Revenue received in Last five Years from Sand Scooping Activity ................... 14 5. Details of Production of Sand in last five years ................................................................................... 15 6. Process of Deposition of Sediments in the rivers of the District ........................................................ 15 7. General Profile of the District .............................................................................................................. 25 8. Land utilization pattern in district ........................................................................................................ 27 9. Physiography of the District ................................................................................................................ -

Actemra Customer List
Actemra Customer List Description District Name 1 Street City Postal Code E-Mail Address Telephone Maharashtra THANE A.N. PHARMA G1/G2, KANTI EMPIRE,LAL GODOWN, VASAI (W) 401202 [email protected] 9028088463 COLLEGE ROAD,VASAI (W),THANE.LBT NO 67 343 2011 Maharashtra MUMBAI ATOR HEALTHCARE PVT. LTD. SONMUR APARTMENTS,DARUWALLA MALAD (W) 400064 [email protected] 022-28662979 / 8 COMPOUND,S.V.ROAD,MALAD (W), MUMBAI Maharashtra PUNE AAKANKSHA LOGISTICS PRIVATE LTD 1ST FLOOR,C\O MANTRI HOSPITALSURVEY PUNE 411036 [email protected] 9822007606 NO 69 15.B.T. KAWADE ROADGHORPADIPUNE Andra Pradesh KRISHNA DISTRICT AUROBINDO DRUGS D.NO:8-72, BLOCK-IIPRASAD VIJAYAWADA 520007 [email protected] 0866-3202242 PLAZA,KAMAIAHTHOPU CENTER,M.G. ROADVIJAYAWADA Maharashtra WASHIM AJAY AGENCIES PATNI CHOWK,WASHIMWASHIM WASHIM 444505 [email protected] 07252 - 234699 2 Maharashtra JALGAON ANAND AGENCIES (CHQ) C.S NO 3297/A/11A, ANAND NIWAS BHUSAWAL 425201 [email protected] 02582-225569/ FIRSNEAR PANDURANG TALKIES JAMNER RDBHUSAWAL 425201 Maharashtra AURNGABAD ANIL MEDICAL STORES SHOP NO.01, HOUSE NO.3-10-53 CST AURNGABAD 431001 [email protected] 9890053040 NOGANDHI CHOWK, AURNGABAD.TAL AURNGABAD DIST. AURANGABADPIN : 431 001 Maharashtra SOLAPYR APTE AGENCIES, (CHQ) 729/3/4 CHATRAPATI COLONYKURDUWADI BARSHI 413401 [email protected] 02184-222543/ 90 ROADBARSHIDIST SOLAPUR Maharashtra YAVATMAL APEX PHARMA HALL NO. 3 , 2 ND FLOORNAGAR PARISHAD YAVATMAL 445001 [email protected] 07232-250317 25 COMPLEX,DATTA CHOWK,YAWATMAL Gujarat AHMEDABAD ANGI AGENCY GF-39,STATION ROADSHIVGANGA AHMEDABAD 382220 [email protected] 9825931530 COMPLEXBALVA Gujarat SURAT A.B.C. DISTRIBUTORS 401/402/403SURAT DAWA SURAT 395004 [email protected] 9825861920 BAZARVASTADEVDI RDKATARGAMSURAT Gujarat JAMNAGAR AMAR ENTERPRISE IST FLOOR, MINAL SHOPPING JAMNAGAR 361005 [email protected] 288-2557207/6455001 CENTRESUMAIR CLUB RD,JAMNAGARTELE 0288 2557207 2550151(R)02882563127 Gujarat GANDHINAGAR ANKUR DISTRIBUTORS 8. -

(River/Creek) Station Name Water Body Latitude Longitude NWMP
NWMP STATION DETAILS ( GEMS / MINARS ) SURFACE WATER Station Type Monitoring Sr No Station name Water Body Latitude Longitude NWMP Project code (River/Creek) Frequency Wainganga river at Ashti, Village- Ashti, Taluka- 1 11 River Wainganga River 19°10.643’ 79°47.140 ’ GEMS M Gondpipri, District-Chandrapur. Godavari river at Dhalegaon, Village- Dhalegaon, Taluka- 2 12 River Godavari River 19°13.524’ 76°21.854’ GEMS M Pathari, District- Parbhani. Bhima river at Takli near Karnataka border, Village- 3 28 River Bhima River 17°24.910’ 75°50.766 ’ GEMS M Takali, Taluka- South Solapur, District- Solapur. Krishna river at Krishna bridge, ( Krishna river at NH-4 4 36 River Krishna River 17°17.690’ 74°11.321’ GEMS M bridge ) Village- Karad, Taluka- Karad, District- Satara. Krishna river at Maighat, Village- Gawali gally, Taluka- 5 37 River Krishna River 16°51.710’ 74°33.459 ’ GEMS M Miraj, District- Sangli. Purna river at Dhupeshwar at U/s of Malkapur water 6 1913 River Purna River 21° 00' 77° 13' MINARS M works,Village- Malkapur,Taluka- Akola,District- Akola. Purna river at D/s of confluence of Morna and Purna, at 7 2155 River Andura Village, Village- Andura, Taluka- Balapur, District- Purna river 20°53.200’ 76°51.364’ MINARS M Akola. Pedhi river near road bridge at Dadhi- Pedhi village, 8 2695 River Village- Dadhi- Pedhi, Taluka- Bhatkuli, District- Pedhi river 20° 49.532’ 77° 33.783’ MINARS M Amravati. Morna river at D/s of Railway bridge, Village- Akola, 9 2675 River Morna river 20° 09.016’ 77° 33.622’ MINARS M Taluka- Akola, District- Akola. -

Congress Activities 1942
Congress Activities Congress Activities 1942 During the fortnight, under review, Bardoli was the scene of Considerable Congress activity. Large crowds witnessed with enthusiasm the arrival of the more important Congress leaders. The meeting of the All India Spinners' Association was held in camera on December 17th, 18th and 19th. It is understood that M. K. Gandhi suggested that war conditions provided an excellent opportunity for the spread of the use of Khaddar. Practical plans were discussed for the extension and improvement of the activities of the Association. The Congress Working Committee sat from December 23rd to December 30th and the resolution which was finally passed has appeared in the press. On December 26th, a public meeting was held at Bardoli which was attended by about 25,000 persons. M. K, Gandhi delivered a brief speech on the importance of the constructive programme and invited a study of his pamphlet on the subject. He expressed himself as not satisfied with the progress made in spinning by local Congressmen. Vsllabhbhai J. Patel, Moulana Abdul Kalam Azad, Pandit Jawaharlal Nehru, Abdul Gafar Khan, Dr. Khan, Govind Vallabh Pant and Bhulabhai J. Desai delivered brief speeches in the course of which they explained that the approach of the war to India had created difficulties for the leaders responsible for Congress policy, but counselled faith in the Congress cause and asked their audience to await further instructions. They avoided giving any hint as to the nature of the Working Committee's deliberations. On December 31st, a meeting was held at Surat which was attended by about 30,000 persons, Pandit Jawaharlal Nehru, who was the chief speaker, referring to the Working Committee resolution deprecated misleading comments which had appeared in the press. -

Study of Fish Diversity in Nira River A
J Indian Fish. Assoc., 34:15- 19, 2007 15 STUDY OF FISH DIVERSITY IN NIRA RIVER A. N. Shendge Deparflnent ofZoology} Tuljaram Chaturchand College} Baramati- 413 1 02} India ABSTRACT Fish diversity in Nira River in Pune District has been studied. The study revealed the presence of 24 species of fish belonging to eight orders (Cypriniformes, Siluriformes, Perciformes, Osteoglossiformes, Synbranchiformes, Clupeiformes, Mugiliformes and Aulopiformes). The predominant orders of fishes in this area (Sangavi) are Cypriniformes, Siluriformes and Perciformes. The highest number of ten species was recorded in the order Cypriniformes. The fishes recorded were found to be widely distributed and were present in good numbers in the river. Keywords: Nira River, Sangavi, Cypriniformes, Siluriformes, Perciformes INTRODUCTION inhabitants and 1570 are marine. In terms The Indian subcontinent has a large of habitat diversity, fishes live in almost number of rivers. In peninsular India, every conceivable aquatic habitat. It is there are large rivers like Godavari, roughly estimated that India alone Krishna, Cauvery, Bhima, etc. These harbours 120,000 known and perhaps principal rivers including their main another 400,000 as yet undescribed tributaries have a total length of about species of fauna and flora distributed over 27,359 km. These along with the canals the country's 320 million hectares of land and irrigation channels having a length of (Sugunan, 1995). Considerable studies on 112,654 km, form a network throughout fish diversity in different freshwater the country and add considerably to the bodies of India have been carried out country's capture fisheries resources during the last few decades.For the survey (Jain, 1986).