The Far Field Hubble Constant
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Further Definition of the Mass-Metallicity Relation In
Further Definition of the Mass-Metallicity Relation in Globular Cluster Systems Around Brightest Cluster Galaxies Robert Cockcroft Department of Physics and Astronomy, McMaster University, Hamilton, Ontario, L8S 4M1, Canada [email protected] William E. Harris Department of Physics and Astronomy, McMaster University, Hamilton, Ontario, L8S 4M1, Canada [email protected] Elizabeth M. H. Wehner Utrecht University, PO Box 80125, 3508 TC Utrecht, The Netherlands [email protected] Bradley C. Whitmore Space Telescope Science Institute, 3700 San Martin Drive, Baltimore MD 21218 [email protected] and Barry Rothberg arXiv:0906.2008v1 [astro-ph.CO] 10 Jun 2009 Naval Research Laboratory, Code 7211, 4555 Overlook Ave SW, Washington D.C. 20375 [email protected] ABSTRACT We combine the globular cluster data for fifteen Brightest Cluster Galaxies and use this material to trace the mass-metallicity relations (MMR) in their glob- ular cluster systems (GCSs). This work extends previous studies which correlate the properties of the MMR with those of the host galaxy. Our combined data sets –2– show a mean trend for the metal-poor (MP) subpopulation which corresponds to a scaling of heavy-element abundance with cluster mass Z ∼ M0.30±0.05. No trend is seen for the metal-rich (MR) subpopulation which has a scaling relation that is consistent with zero. We also find that the scaling exponent is independent of the GCS specific frequency and host galaxy luminosity, except perhaps for dwarf galaxies. We present new photometry in (g’,i’) obtained with Gemini/GMOS for the globular cluster populations around the southern giant ellipticals NGC 5193 and IC 4329. -

A New X-Ray Selected Sample of Very Extended Galaxy Groups from the ROSAT All-Sky Survey Weiwei Xu1, 2, 3, Miriam E
Astronomy & Astrophysics manuscript no. main c ESO 2018 September 11, 2018 A New X-ray Selected Sample of Very Extended Galaxy Groups from the ROSAT All-Sky Survey Weiwei Xu1; 2; 3, Miriam E. Ramos-Ceja2, Florian Pacaud2, Thomas H. Reiprich2, and Thomas Erben2 1 National Astronomical Observatories, Chinese Academy of Sciences, Beijing, China (e-mail: [email protected]) 2 Argelander-Insitut für Astronomie, Universität Bonn, Bonn, Germany 3 University of Chinese Academy of Sciences, Beijing, China Accepted by A&A ABSTRACT Context. Some indications for tension have long been identified between cosmological constraints obtained from galaxy clusters and primary cosmic microwave background (CMB) measurements. Typically, assuming the matter density and fluctuations, as parameterized with Ωm and σ8, estimated from CMB measurements, many more clusters are expected than those actually observed. This has been reinforced recently by the Planck collaboration. One possible explanation could be that certain types of galaxy groups or clusters were missed in samples constructed in previous surveys, resulting in a higher incompleteness than estimated. Aims. In this work, we aim to determine if a hypothetical class of very extended, low surface brightness, galaxy groups or clusters have been missed in previous X-ray cluster surveys based on the ROSAT All-Sky Survey (RASS). Methods. We applied a dedicated source detection algorithm sensitive also to more unusual group or cluster surface brightness distributions. It includes a multiresolution filtering, a source detection algorithm, and a maximum likelihood fitting procedure. To optimize parameters, this algorithm is calibrated using extensive simulations before it is used to reanalyze the RASS data. -

Institute for Astronomy University of Hawai'i at M¯Anoa Publications In
Institute for Astronomy University of Hawai‘i at Manoa¯ Publications in Calendar Year 2009 Abazajian, K. N., et al., including Hoblitt, J., Magnier, E., Bagatin, A. C., Michel, P., & Bus, S. J. Preface to Special Is- Pope, A. C., Price, P. A., Szapudi, I. The Seventh Data sue VII Workshop on Catastrophic Disruption in the Solar Release of the Sloan Digital Sky Survey. ApJS, 182, 543– System. Planet. Space Sci., 57, 109–110 (2009) 558 (2009) Bakos, G. A., Howard, A. W., Noyes, R. W., Hartman, J., Akeson, R., et al., including Johnson, J. The Value of Torres, G., Kovacs,´ G., Fischer, D. A., Latham, D. W., the Keck Observatory to NASA and Its Scientific Com- Johnson, J. A., et al. HAT-P-13b,c: A Transiting Hot munity. astro2010: The Astronomy and Astrophysics Jupiter with a Massive Outer Companion on an Eccentric Decadal Survey, 2010, no. 1P (2009) Orbit. ApJ, 707, 446–456 (2009) Alcock, C., including Kudritzki, R.-P. Statement from AC- Bakos, G. A.,´ et al., including Johnson, J. A. HAT-P-10b: A CORD for ASTRO2010. astro2010: The Astronomy and Light and Moderately Hot Jupiter Transiting A K Dwarf. Astrophysics Decadal Survey, 2010, no. 27P (2009) ApJ, 696, 1950–1955 (2009) Allers, K. N., Liu, M. C., Shkolnik, E., Cushing, Bally, J., Walawender, J., Reipurth, B., & Megeath, S. T. M. C., Dupuy, T. J., Mathews, et al. 2MASS Outflows and Young Stars in Orion’s Large Cometary 22344161+4041387AB: A Wide, Young, Accreting, Clouds L1622 and L1634. AJ, 137, 3843–3858 (2009) Low-Mass Binary in the LkHα233 Group. -
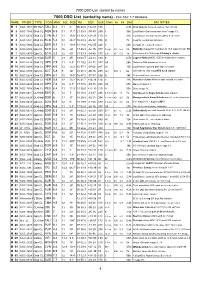
DSO List V2 Current
7000 DSO List (sorted by name) 7000 DSO List (sorted by name) - from SAC 7.7 database NAME OTHER TYPE CON MAG S.B. SIZE RA DEC U2K Class ns bs Dist SAC NOTES M 1 NGC 1952 SN Rem TAU 8.4 11 8' 05 34.5 +22 01 135 6.3k Crab Nebula; filaments;pulsar 16m;3C144 M 2 NGC 7089 Glob CL AQR 6.5 11 11.7' 21 33.5 -00 49 255 II 36k Lord Rosse-Dark area near core;* mags 13... M 3 NGC 5272 Glob CL CVN 6.3 11 18.6' 13 42.2 +28 23 110 VI 31k Lord Rosse-sev dark marks within 5' of center M 4 NGC 6121 Glob CL SCO 5.4 12 26.3' 16 23.6 -26 32 336 IX 7k Look for central bar structure M 5 NGC 5904 Glob CL SER 5.7 11 19.9' 15 18.6 +02 05 244 V 23k st mags 11...;superb cluster M 6 NGC 6405 Opn CL SCO 4.2 10 20' 17 40.3 -32 15 377 III 2 p 80 6.2 2k Butterfly cluster;51 members to 10.5 mag incl var* BM Sco M 7 NGC 6475 Opn CL SCO 3.3 12 80' 17 53.9 -34 48 377 II 2 r 80 5.6 1k 80 members to 10th mag; Ptolemy's cluster M 8 NGC 6523 CL+Neb SGR 5 13 45' 18 03.7 -24 23 339 E 6.5k Lagoon Nebula;NGC 6530 invl;dark lane crosses M 9 NGC 6333 Glob CL OPH 7.9 11 5.5' 17 19.2 -18 31 337 VIII 26k Dark neb B64 prominent to west M 10 NGC 6254 Glob CL OPH 6.6 12 12.2' 16 57.1 -04 06 247 VII 13k Lord Rosse reported dark lane in cluster M 11 NGC 6705 Opn CL SCT 5.8 9 14' 18 51.1 -06 16 295 I 2 r 500 8 6k 500 stars to 14th mag;Wild duck cluster M 12 NGC 6218 Glob CL OPH 6.1 12 14.5' 16 47.2 -01 57 246 IX 18k Somewhat loose structure M 13 NGC 6205 Glob CL HER 5.8 12 23.2' 16 41.7 +36 28 114 V 22k Hercules cluster;Messier said nebula, no stars M 14 NGC 6402 Glob CL OPH 7.6 12 6.7' 17 37.6 -03 15 248 VIII 27k Many vF stars 14.. -

Further Definition of the Mass-Metallicity Relation
GLOBULAR CLUSTER SYSTEMS IN BRIGHTEST CLUSTER GALAXIES: FURTHER DEFINITION OF THE MASS-METALLICITY RELATION By ROBERT COCKCROFT, M.SCI. GLOBULAR CLUSTER SYSTEMS IN BRIGHTEST CLUSTER GALAXIES: FURTHER DEFINITION OF THE MASS-METALLICITY RELATION By ROBERT COCKCROFT, M.SCI. A Thesis Submitted to the School of Graduate Studies in Partial Fulfilment of the Requirements for the Degree Master of Science McMaster University @Copyright by Robert Cockcroft, May 2008 MASTER OF SCIENCE (2008) McMaster University (Department of Physics and Astronomy) Hamilton, Ontario TITLE: Globular Cluster Systems in Brightest Cluster Galaxies: Further Definition of the Mass-Metallicity Relation AUTHOR: Robert Cockcroft, M.Sci. SUPERVISOR: Prof. William E. Harris NUMBER OF PAGES: xii, 111 ii Abstract Globular clusters (GCs) can be divided into two subpopulations when plot ted on a colour-magnitude diagram: one red and metal-rich (MR), and the other blue and metal-poor (MP). For each subpopulation, any correlation between colour and luminosity can then be converted into mass-metallicity relations (MM Rs). Tracing the MMRs for fifteen GC systems ( GCSs) - all around Brightest Cluster Galaxies - we see a nonzero trend for the MP subpopulation but not the MR. This trend is characterised by p in the relation Z=M'. We find p V"I 0.35 for the MP GCs, and a relation for the MR GCs that is consistent with zero. When we look at how this trend varies with the host galaxy luminosity, we extend previous studies (e.g., Mieske et al, 2006b) into the bright end of the host galaxy sample. In addition to previously presented (B-1) photometry for eight GCSs ob tained with ACS/WFC on the HST, we present seven more GCSs. -

[email protected] Current As of January 24, 2019
PUBLICATIONS:SAURABH W. JHA [email protected] current as of January 24, 2019 Journal Articles 169 “K2 Observations of SN 2018oh Reveal a Two-component Rising Light Curve for a Type Ia Supernova,” Dimitriadis, G., R. J. Foley, A. Rest, D. Kasen, A. L. Piro, A. Polin, D. O. Jones, A. Villar, G. Narayan, D. A. Coulter, C. D. Kilpatrick, Y.-C. Pan, C. Rojas-Bravo, O. D. Fox, S. W. Jha, P. E. Nugent, A. G. Riess, D. Scolnic, M. R. Drout, G. Barentsen, J. Dotson, M. Gully-Santiago, C. Hedges, A. M. Cody, T. Barclay, S. Howell, P. Garnavich, B. E. Tucker, E. Shaya, R. Mushotzky, R. P. Olling, S. Margheim, A. Zenteno, J. Coughlin, J. E. Van Cleve, J. V. d. M. Cardoso, K. A. Larson, K. M. McCalmont-Everton, C. A. Peterson, S. E. Ross, L. H. Reedy, D. Osborne, C. McGinn, L. Kohnert, L. Migliorini, A. Wheaton, B. Spencer, C. Labonde, G. Castillo, G. Beerman, K. Steward, M. Hanley, R. Larsen, R. Gangopadhyay, R. Kloetzel, T. Weschler, V. Nystrom, J. Moffatt, M. Redick, K. Griest, M. Packard, M. Muszynski, J. Kampmeier, R. Bjella, S. Flynn, B. Elsaesser, K. C. Cham- bers, H. A. Flewelling, M. E. Huber, E. A. Magnier, C. Z. Waters, A. S. B. Schultz, J. Bulger, T. B. Lowe, M. Willman, S. J. Smartt, K. W. Smith, S. Points, G. M. Strampelli, J. Brima- combe, P. Chen, J. A. Muñoz, R. L. Mutel, J. Shields, P. J. Vallely, S. Villanueva Jr., W. Li, X. Wang, J. Zhang, H. Lin, J. Mo, X. -

L'indien – Le MICROSCOPE
L’Indien – Le Microscope Ces constellations ne contiennent pas d'objet céleste observable avec un équipement amateur. Hémisphère Sud Le CAPRICORNE Gamma Galaxie 4,67 N 6925 L’INDIEN – Le MICROSCOPE Alpha 4,87 Le SAGITTAIRE Le POISSON AUSTRAL Lacaille 8760 6,67 Distance 12,9 a.l. 3 Alpha La GRUE 3,11 Galaxie N 8760 Galaxie Galaxie N 7041 Le TELESCOPE N 7049 Galaxie IC 5152 Galaxie Βeta 3,67 Le TOUCAN N7090 Delta Galaxie 4,4 Galaxie N7141 superamas de galaxies du Paon-Indien 200 millions a.l. Epsilon 11,82 années-lumière Le PAON L’OCTANT constellations de l'hémisphère Sud. introduite par Nicolas-Louis de Lacaille en 1752 Les distances qui nous séparent des étoiles Les distances qui nous séparent des Galaxies Le superamas Paon-Indien, aussi appelé superamas du Paon, est un superamas de galaxies voisin du superamas local (qui contient la Voie lactée). Ce superamas est située entre 210 et 260 millions d'années- lumière (entre 64 et 78 mégaparsecs). Il contient trois principaux amas : Abell 3656, Abell 3698, le plus dense, et Abell 3742. Il fait partie d'un mur de galaxies assez proche qui relie l'amas de la Règle au superamas du Centaure. Une publication de 2014 émet l'hypothèse que ce superamas serait juste un lobe de Laniakea, un superamas plus grand centré sur le Grand Attracteur qui contient également le superamas de la Vierge dont nous faisons partie. 465 Millions a.l. Abell S0740 L'Indien, ou Oiseau indien[réf. nécessaire], est une constellation de l'hémisphère sud. -

Cosmologia Da Origem Ao Fim Do Universo 2015
Ensino a Distância COSMOLOGIA Da origem ao fim do universo 2015 Módulo 3 A Teoria relativistica da Gravitação e a nova visão do conteúdo do universo Presidente da República Equipe de realização Dilma Vana Rousseff Conteúdo científico e texto Ministro de Estado da Ciência, Tecnologia e Inovação Carlos Henrique Veiga José Aldo Rebelo Figueiredo Secretário-Executivo do Ministério da Ciência, Tecnologia e Inovação Projeto gráfico, editoração e capa Álvaro Doubes Prata Vanessa Araújo Santos Subsecretário de Coordenação de Unidades de Pesquisas Web Design Kayo Júlio César Pereira Giselle Veríssimo Diretor do Observatório Nacional Caio Siqueira da Silva João Carlos Costa dos Anjos Colaboradores Observatório Nacional/MCTI (Site: www.on.br) Alexandra Pardo Policastro Natalense Rua General José Cristino, 77 Ney Avelino B. Seixas São Cristóvão, Rio de Janeiro - RJ Alex Sandro de Souza de Oliveira CEP: 20921-400 Criação, Produção e Desenvolvimento (Email: [email protected]) Esta publicação é uma homenagem a Antares Cleber Crijó (1948 - 2009) que dedicou boa parte da sua carreira científica à divulgação e popularização da ciência astronômica. Carlos Henrique Veiga © 2015 Todos os direitos reservados ao Cosme Ferreira da Ponte Neto Observatório Nacional. Rodrigo Cassaro Resende Silvia da Cunha Lima Vanessa Araújo Santos Giselle Veríssimo Caio Siqueira da Silva Luiz Felipe Gonçalves de Souza Imagem do Grande Aglomerado Globular da Constelação de Hércules. Mostra uma grande diversidade de galáxias em in- teração. Foi descoberto pelo inglês Edmond Halley em 1714. Está a uma distância de 25100 anos-luz do Sistema Solar. Pode conter mais de um milhão de estrelas Ensino à Distância COSMOLOGIA Da origem ao fim do universoo 2015 Módulo 3 A Teoria relativística da Gravitação e a nova visão do conteúdo do universo O “DESLOCAMENTO PARA O VERMELHO” (REDSHIFT) Apresentaremos alguns detalhes de um dos conceitos mais importantes no estudo da astronomia extragaláctica e da cosmologia: o “deslocamento para 20 o vermelho” ou “redshift”. -

And-Andromeda-V1 Ant-Antlia-V1 Aps-Apus-V1
AND-ANDROMEDA-V1 1 1 IC 1535 00 14.0 +48 10 AND GALXY S 15.1m 1.3'X0.3' 170º 59-4 3 9 NGC 529 01 25.7 +34 43 AND GALXY E-SO 12.1m 2.4'X2.1' 160º 91-4 2 NGC 51 00 14.6 +48 15 AND GALXY S0Pec 13.1m 1.7'X1.4' 59-4 4 1 Hickson 10 01 26.4 +34 42 AND GALCL NGC536 12.6m 91-4 3 NGC 70 00 18.4 +30 05 AND GALXY Sbc 13.5m 1.6'X1.4' 0º 89-4 2 NGC 536 01 26.4 +34 42 AND GALXY SBb 12.3m 3.0'X1.1' 62º 91-4 4 NGC 80 00 21.2 +22 21 AND GALXY E-SO 12.1m 2.2'X2.0' 126- 4 3 M1-1 01 37.3 +50 28 AND PLNNB 14.3m 6'' 37-1 5 NGC 83 00 21.4 +22 26 AND GALXY E0 12.5m 1.3'X1.2' 126- 4 4 NGC 679 01 49.7 +35 47 AND GALXY SO 12.3m 2.1'X2.1' 92-4 6 NGC 97 00 22.5 +29 45 AND GALXY E 12.3m 1.5'X1.3' 90-4 5 NGC 687 01 50.6 +36 22 AND GALXY SO 12.3m 1.4'X1.4' 92-4 7 NGC 108 00 26.0 +29 13 AND GALXY SBO-a 12.1m 2.0'X1.6' 90-4 6 AGC 262 01 52.8 +36 12 AND GALCL NGC708 13.3m 92-4 8 Hickson 1 00 26.1 +25 42 AND GALCL UGC248 14.4m 126- 4 7 NGC 753 01 57.7 +35 55 AND GALXY SBbc 12.3m 2.5'X2.0' 125º 92-4 9 And III 00 35.4 +36 31 AND GALXY dE2 13.5m 90-4 8 NGC 752 01 57.7 +37 47 AND OPNCL III1m 5.6m 50' 60* 9.0br 92-4 2 1 IC 1559 00 36.9 +23 59 AND GALXY LM 14.6m 0.8'X0.4' 94º 4628.0RV 126- 4 9 NGC 812 02 06.8 +44 34 AND GALXY Sbc 11.1m 9.3'X2.2' 160º 62-4 2 NGC 169 00 36.9 +23 60 AND GALXY Sb 13.1m 2.9'X0.8' 88º 126- 4 5 1 UGC 1626 02 08.4 +41 29 AND GALXY SB 14.1m 1.5'X1.5' 5543.0RV 62-4 3 NGC 183 00 38.5 +29 31 AND GALXY E 12.6m 2.1'X1.6' 130º 90-4 2 NGC 818 02 08.7 +38 47 AND GALXY SBbc 12.5m 2.9'X1.2' 113º 92-4 4 M 110 00 40.4 +41 41 AND GALXY E6 8.1m 19.5'X11.5' 170º 60-4 -
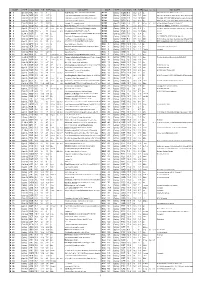
7000 List by Name
NAME TYPE CON MAG S.B. SIZE Class ns bs SAC NOTES NAME TYPE CON MAG S.B. SIZE Class ns bs SAC NOTES M 1 SN Rem TAU 8.4 11 8' Crab Nebula; filaments;pulsar 16m;3C144 -M 99 Galaxy COM 9.9 13.2 5.3' Sc SN 1967h;Norton-diff for small scope M 2 Glob CL AQR 6.5 11 11.7' II Lord Rosse-Dark area near core;* mags 13... -M 100 Galaxy COM 9.4 13.4 7.5' SBbc SN 1901-14-59;NGC 4322 @ 5.2';NGC 4328 @ 6.1' M 3 Glob CL CVN 6.3 11 18.6' VI Lord Rosse-sev dark marks within 5' of center -M 101 Galaxy UMA 7.9 14.9 28.5' SBc P w NGC 5474;SN 1909;spir galax w one heavy arm; M 4 Glob CL SCO 5.4 12 26.3' IX Look for central bar structure -M 102 Galaxy DRA 9.9 12.2 6.5' Sa vBN w dk lane and ansae;NGC 5867 small E neb; M 5 Glob CL SER 5.7 11 19.9' V st mags 11...;superb cluster -M 103 Opn CL CAS 7.4 11 6' III 2 p 40 10.6 in Cas OB8;incl Struve 131 6-9m 14'' M 6 Opn CL SCO 4.2 10 20' III 2 p 80 6.2 Butterfly cluster;51 members to 10.5 mag incl var*- BMM104 Sco Galaxy VIR 8 11.6 8.6' Sab Sombrero Galaxy; H I 43;dark equatorial lane; M 7 Opn CL SCO 3.3 12 80' II 2 r 80 5.6 80 members to 10th mag; Ptolemy's cluster -M 105 Galaxy LEO 9.3 12.8 5.3' E1 P w NGC 3384 @ 7.2';NGC 3389 @ 10 ';Leo Group M 8 Opn CL SGR 4.6 - 15' II 2 m n 6.9 In Lagoon nebula M8;25* mags 7..