Supplementary Information For
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Hbo Premieres the Third Season of Game of Thrones
HBO PREMIERES THE THIRD SEASON OF GAME OF THRONES The new season will premiere simultaneously with the United States on March 31st Miami, FL, March 18, 2013 – The battle for the Iron Throne among the families who rule the Seven Kingdoms of Westeros continues in the third season of the HBO original series, Game of Thrones. Winner of two Emmys® 2011 and six Golden Globes® 2012, the series is based on the famous fantasy books “A Song of Ice and Fire” by George R.R. Martin. HBO Latin America will premiere the third season simultaneously with the United States on March 31st. Many of the events that occurred in the first two seasons will culminate violently, with several of the main characters confronting their destinies. But new challengers for the Iron Throne rise from the most unexpected places. Characters old and new must navigate the demands of family, honor, ambition, love and – above all – survival, as the Westeros civil war rages into autumn. The Lannisters hold absolute dominion over King’s Landing after repelling Stannis Baratheon’s forces, yet Robb Stark –King of the North– still controls much of the South, having yet to lose a battle. In the Far North, Mance Rayder (new character portrayed by Ciaran Hinds) has united the wildlings into the largest army Westeros has ever seen. Only the Night’s Watch stands between him and the Seven Kingdoms. Across the Narrow Sea, Daenerys Targaryen – reunited with her three growing dragons – ventures into Slaver’s Bay in search of ships to take her home and allies to conquer it. -

GAME of THRONES® the Follow Tours Include Guides with Special Interest and a Passion for the Game of Thrones
GAME OF THRONES® The follow tours include guides with special interest and a passion for the Game of Thrones. However you can follow the route to explore the places featured in the series. Meet your Game of Thrones Tours Guide Adrian has been a tour guide for many years, with a passion for Game of Thrones®. During filming he was an extra in various scenes throughout the series, most noticeably, a stand in double for Ser Davos. He is also clearly seen guarding Littlefinger before his final demise at the hands of the Stark sisters in Winterfell. Adrian will be able to bring his passion alive through his experience, as well as his love of Northern Ireland. Cairncastle ~ The Neck & North of Winterfell 1 Photo stop of where Sansa learns of her marriage to Ramsay Bolton, and also where Ned beheads Will, the Night’s Watch deserter. Cairncastle Refreshment stop at Ballygally Castle, Ballygally Located on the scenic Antrim coast facing the soft, sandy beaches of Ballygally Bay. The Castle dates back to 1625 and is unique in that it is the only 17th Century building still used as a residence in Northern Ireland today. The hotel is reputedly haunted by a friendly ghost and brave guests can visit the ‘ghost room’ in one of the towers to see for themselves. View Door No. 9 of the Doors of Thrones and collect your first stamp in your Journey of Doors passport! In the hotel foyer you will be able to admire the display cabinets of the amazing Steensons Game of Thrones® inspired jewellery. -

Representações Femininas Em Game of Thrones: Mediações Entre Os Sete Reinos E a Contemporaneidade
Representações femininas em Game of Thrones: mediações entre os Sete Reinos e a Contemporaneidade Representações femininas em Game of Thrones: mediações entre os Sete Reinos e a Contemporaneidade1 Andréa Corneli Ortis Doutoranda; Universidade Federal de Santa Maria, Santa Maria, RS, Brasil ORCID: https://orcid.org/0000-0002-9865-8411 Flavi Ferreira Lisbôa Filho Doutor; Universidade Federal de Santa Maria, Santa Maria, RS, Brasil ORCID: https://orcid.org/0000-0003-4307-9401 Resumo A presente pesquisa questiona como são representadas as identidades femininas da personagem Sansa Stark, de Game of Thrones, e quais sentidos sobre o feminino contemporâneo são mobilizados pela série. Para isso, buscamos observar nosso objeto através da categoria personagem e interações por meio da análise textual proposta por Casetti e Chio (1999). Após isso, acionamos o conceito de mediação, advindo de um cotejamento entre Williams (1979), Orózco-Gómez (1997) e Martín-Barbero (2001), por meio das categorias gênero, competência e moralidade pública, e percebemos que a série busca problematizar tipos de violência que acontecem na contemporaneidade em relação ao feminino, como sexual, psicológica ou física, casamento infantil e mulher como moeda de troca. Assim, ao longo das temporadas, a personagem é retratada de modo a ascender, porém somente após passar por inúmeros tipos de violência. Portanto, os sentidos negociados entre a ficção e a realidade presentes em Sansa, na série, são formadas de acordo com o ambiente em que vive, valores sociais e privados impostos pela sociedade. Palavras-chave Identidade feminina. Gênero. Representação. Mediações. Game of Thrones. 1 Introdução É cada vez mais difícil tornar-se mulher na sociedade contemporânea, fato que vai de encontro aos tantos anos de lutas que foram travadas para tentar vivermos de maneira 1 Este trabalho é um recorte da dissertação de mestrado de mesmo título. -
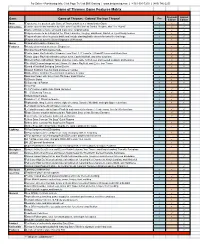
Game of Thrones Feature Matrix
For Sales + Purchasing Info, Click Page To Visit BMI Gaming | www.bmigaming.com | + 561-391-7200 | (800) 746-2255 Game of Thrones Game Features Matrix Premium Limited Pro Game Game of Thrones - Defend The Iron Throne! Edition Edition Main Experience the greatest epic Game of Thrones battles in a World Under Glass Attractions Custom speech and narration by GOT actor Rory McCann as Sandor Clegane, aka "The Hound" Game of Thrones theme song and many more original songs Players choose to be a Knight of the Stark, Lannister, Greyjoy, Baratheon, Martell, or Tyrell family houses Players choose other houses to battle and include stacking battle choices for twice the challenge Players strive to rule the Seven Kingdoms of Westeros Game Animated interactive Dragon toy Features Motorized animated interactive Dragon toy Exciting Sword Fight display mode Castle Upper Playfield with 2 Flippers, Loop Shot, 3 .5" Targets, 2 Drop-Off Lanes and Moon Door Castle Upper Playfield embodies unique rules, Castle Multiball, and other surprises Battering Ram sliding Bash Target smashes Castle Gate for bonuses and needed weapons and features The Wall Elevator brings ball up 2 floors: (1) Upper Playfield, and (2) the Iron Throne Sword of Multiball Swinging Sword Device Dragon Kickback fires ball back at players in anger White Walker Kickback fires ball back at players in anger Spinning Target with Sync-Flash TM Super bright Flasher 2 Electric Gates 2 Superspeed Ramps 1 Up Post 1-1.5" Custom Castle Gate Stand Up target -

El Ecosistema Narrativo Transmedia De Canción De Hielo Y Fuego”
UNIVERSITAT POLITÈCNICA DE VALÈNCIA ESCOLA POLITE CNICA SUPERIOR DE GANDIA Grado en Comunicación Audiovisual “El ecosistema narrativo transmedia de Canción de Hielo y Fuego” TRABAJO FINAL DE GRADO Autor/a: Jaume Mora Ribera Tutor/a: Nadia Alonso López Raúl Terol Bolinches GANDIA, 2019 1 Resumen Sagas como Star Wars o Pokémon son mundialmente conocidas. Esta popularidad no es solo cuestión de extensión sino también de edad. Niñas/os, jóvenes y adultas/os han podido conocer estos mundos gracias a la diversidad de medios que acaparan. Sin embargo, esta diversidad mediática no consiste en una adaptación. Cada una de estas obras amplia el universo que se dio a conocer en un primer momento con otra historia. Este conjunto de historias en diversos medios ofrece una narrativa fragmentada que ayuda a conocer y sumergirse de lleno en el universo narrativo. Pero a su vez cada una de las historias no precisa de las demás para llegar al usuario. El mundo narrativo resultante también es atractivo para otros usuarios que toman parte de mismo creando sus propias aportaciones. A esto se le conoce como narrativa transmedia y lleva siendo objeto de estudio desde principios de siglo. Este trabajo consiste en el estudio de caso transmedia de Canción de Hielo y Fuego la saga de novelas que posteriormente se adaptó a la televisión como Juego de Tronos y que ha sido causa de un fenómeno fan durante la presente década. Palabras clave: Canción de Hielo y Fuego, Juego de Tronos, fenómeno fan, transmedia, narrativa Summary Star Wars or Pokémon are worldwide knowledge sagas. This popularity not just spreads all over the world but also over an age. -

Archetypes in Female Characters of Game of Thrones
Sveučilište u Zadru Odjel za anglistiku Preddiplomski sveučilišni studij engleskog jezika i književnosti (dvopredmetni) Gloria Makjanić Archetypes in Female Characters of Game of Thrones Završni rad Zadar, 2018. Sveučilište u Zadru Odjel za anglistiku Preddiplomski sveučilišni studij engleskog jezika i književnosti (dvopredmetni) Archetypes in Female Characters of Game of Thrones Završni rad Student/ica: Mentor/ica: Gloria Makjanić dr. sc. Zlatko Bukač Zadar, 2018. Makjanić 1 Izjava o akademskoj čestitosti Ja, Gloria Makjanić, ovime izjavljujem da je moj završni rad pod naslovom Female Archetypes of Game of Thrones rezultat mojega vlastitog rada, da se temelji na mojim istraživanjima te da se oslanja na izvore i radove navedene u bilješkama i popisu literature. Ni jedan dio mojega rada nije napisan na nedopušten način, odnosno nije prepisan iz necitiranih radova i ne krši bilo čija autorska prava. Izjavljujem da ni jedan dio ovoga rada nije iskorišten u kojem drugom radu pri bilo kojoj drugoj visokoškolskoj, znanstvenoj, obrazovnoj ili inoj ustanovi. Sadržaj mojega rada u potpunosti odgovara sadržaju obranjenoga i nakon obrane uređenoga rada. Zadar, 13. rujna 2018. Makjanić 2 Table of Contents 1. Introduction ..................................................................................................................... 3 2. Game of Thrones ............................................................................................................. 4 3. Archetypes ...................................................................................................................... -

“Game of Thrones” Season 5 One Line Cast List NO
“Game of Thrones” Season 5 One Line Cast List NO. CHARACTER ARTIST 1 TYRION LANNISTER PETER DINKLAGE 3 CERSEI LANNISTER LENA HEADEY 4 DAENERYS EMILIA CLARKE 5 SER JAIME LANNISTER NIKOLAJ COSTER-WALDAU 6 LITTLEFINGER AIDAN GILLEN 7 JORAH MORMONT IAIN GLEN 8 JON SNOW KIT HARINGTON 10 TYWIN LANNISTER CHARLES DANCE 11 ARYA STARK MAISIE WILLIAMS 13 SANSA STARK SOPHIE TURNER 15 THEON GREYJOY ALFIE ALLEN 16 BRONN JEROME FLYNN 18 VARYS CONLETH HILL 19 SAMWELL JOHN BRADLEY 20 BRIENNE GWENDOLINE CHRISTIE 22 STANNIS BARATHEON STEPHEN DILLANE 23 BARRISTAN SELMY IAN MCELHINNEY 24 MELISANDRE CARICE VAN HOUTEN 25 DAVOS SEAWORTH LIAM CUNNINGHAM 32 PYCELLE JULIAN GLOVER 33 MAESTER AEMON PETER VAUGHAN 36 ROOSE BOLTON MICHAEL McELHATTON 37 GREY WORM JACOB ANDERSON 41 LORAS TYRELL FINN JONES 42 DORAN MARTELL ALEXANDER SIDDIG 43 AREO HOTAH DEOBIA OPAREI 44 TORMUND KRISTOFER HIVJU 45 JAQEN H’GHAR TOM WLASCHIHA 46 ALLISER THORNE OWEN TEALE 47 WAIF FAYE MARSAY 48 DOLOROUS EDD BEN CROMPTON 50 RAMSAY SNOW IWAN RHEON 51 LANCEL LANNISTER EUGENE SIMON 52 MERYN TRANT IAN BEATTIE 53 MANCE RAYDER CIARAN HINDS 54 HIGH SPARROW JONATHAN PRYCE 56 OLENNA TYRELL DIANA RIGG 57 MARGAERY TYRELL NATALIE DORMER 59 QYBURN ANTON LESSER 60 MYRCELLA BARATHEON NELL TIGER FREE 61 TRYSTANE MARTELL TOBY SEBASTIAN 64 MACE TYRELL ROGER ASHTON-GRIFFITHS 65 JANOS SLYNT DOMINIC CARTER 66 SALLADHOR SAAN LUCIAN MSAMATI 67 TOMMEN BARATHEON DEAN-CHARLES CHAPMAN 68 ELLARIA SAND INDIRA VARMA 70 KEVAN LANNISTER IAN GELDER 71 MISSANDEI NATHALIE EMMANUEL 72 SHIREEN BARATHEON KERRY INGRAM 73 SELYSE -

Questions Are Coming. a Game of Thrones Quiz by Scott Hendrickson
Questions are coming. A Game of Thrones Quiz by Scott Hendrickson 1. What is the motto of House Stark? 2. What phrase do you use to tell a dragon to A) Winter is coming. breath fire? B) It's getting chilly. A) Dothraki. C) Burr, my feet are frozen. B) Dracarys. D) Seriously, do they ever heat this castle? C) Valar doharis. D) Light'em up, bitches! 3. Name Tywin Lannister’s three children. 4. Who are King Joffrey Baratheon’s real parents? ____________________, ____________________, & ____________________ & ____________________ ____________________ 5. What material is the weapon used by 6. Circle the locations that are in Westeros: Samuel Tarly to kill a white walker? Winterfell, Braavos, Dorne, Astapor, The Vale, ________________________________ Valyria, Volantis, King’s Landing, Asshai, Highgarden, Tacoma, Kirkland, 7. Hodor? 8. Who appointed Ned Stark as “Hand of the A) Hodor. King”? B) Hodor? A) Jon Arryn C) Hodor! B) Robert Baratheon D) Any of the above. C) Lord Varys D) Stannis Baratheon E) Tywin Lannister 9. Who initiated King Joffrey’s 10. Circle the names of the five non-bastard assassination? Stark children: A) Margery Tyrell B) Lady Olenna Tyrell Poliver, Sansa, Myrcella, Arya, Tommen, C) Petyr Baelish Rungsigul, Rickon, Robb, Ned, Cersei, Bran, D) Tyrion Lannister Rydon, Jon E) Sansa Stark F) Hodor 11. What are the names of Daenarys 12. What song starts playing before the Targaryan’s three dragons? murders occur at the Red Wedding? A) Dragol, Rhaelar and Viserya A) The Pride of the Lion B) Drogon, Rhaegal and Viserion B) The Bear and the Maiden Fair C) Drogo, Rhaegon and Viserios C) Ours is the fury D) Drogal, Rhaegar, and Viseron D) The Rains of Castamere E) Lucky, Dusty, and Ned E) "Shake it off" by Taylor Swift 13. -

2021 Rittenhouse Archives Game of Thrones Iron
February 24, 2021 2021 Rittenhouse Archives Game of Thrones Iron Anniversary Season 1 Trading Cards: SRP $29.99 Cost: $138.75 per box, 10 boxes‐$129.50 per box, 30 boxes +$127.00 per box Configuration: 10 boxes per case/8 packs per box/6 cards per pack Purchase Order Due Date: 3‐22‐2021 Release Date: 6‐2‐2021 Style #: RA21GOTIAS1 Min. 1 Inscription Autograph Card Per Box! Min. 2 Autograph Cards Per Box Overall Inscription Autographs Card Signers include: Emilia Clarke (Daenerys Targaryen) Mark Addy (King Robert Baratheon) Sophie Turner (Sansa Stark) Conleth Hill (Lord Varys) Alfie Allen (Theon Greyjoy) Gemma Whelan (Yara Greyjoy) Michiel Huisman (Daario Naharis) Tom Hopper (Dickon Tarly) Indira Varma (Ellaria Sand) Conan Stevens (The Mountain) Jack Gleeson (King Joffrey) and many more! Hundreds of Inscription Variations to Collect! Plus Amazing New Bonus Autographs Autograph/Relic/Quote Cards Featuring Emilia Clarke (Daenerys Targaryen) and Peter Dinklage (Tyrion Lannister) Autograph/Quote Cards signed by Sean Bean (Ned Stark) Dual Autograph Cards with Maisie Williams (Arya Stark), Lena Headey (Cersei Lannister), Conleth Hill (Lord Varys), Sean Bean (Ned Stark), Iwan Rheon (Ramsay Bolton), Nathalie Emmanuel (Missandei) and more! Autograph/Relic Cards Signed by Lena Headey (Cersei Lannister) Series 1 Base Set 99 High‐End Cards of Leading Characters, Featuring All‐New, Inter‐Connective Foil‐Stamping and 9‐Card Puzzle‐ Backs! Series 1 Bonus Cards 99 Copper Parallel Base Cards (Numbered) 99 Gold Parallel Base Cards (Numbered) One‐of‐a‐Kind -

Racialization, Femininity, Motherhood and the Iron Throne
THESIS RACIALIZATION, FEMININITY, MOTHERHOOD AND THE IRON THRONE GAME OF THRONES AS A HIGH FANTASY REJECTION OF WOMEN OF COLOR Submitted by Aaunterria Treil Bollinger-Deters Department of Ethnic Studies In partial fulfillment of the requirements For the Degree of Master of Arts Colorado State University Fort Collins, Colorado Fall 2018 Master’s Committee: Advisor: Ray Black Joon Kim Hye Seung Chung Copyright by Aaunterria Bollinger 2018 All Rights Reserved. ABSTRACT RACIALIZATION, FEMININITY, MOTHERHOOD AND THE IRON THRONE GAME OF THRONES A HIGH FANTASY REJECTION OF WOMEN OF COLOR This analysis dissects the historic preconceptions by which American television has erased and evaded race and racialized gender, sexuality and class distinctions within high fantasy fiction by dissociation, systemic neglect and negating artistic responsibility, much like American social reality. This investigation of high fantasy creative fiction alongside its historically inherited framework of hierarchal violent oppressions sets a tone through racialized caste, fetishized gender and sexuality. With the cult classic television series, Game of Thrones (2011-2019) as example, portrayals of white and nonwhite racial patterns as they define womanhood and motherhood are dichotomized through a new visual culture critical lens called the Colonizers Template. This methodological evaluation is addressed through a three-pronged specified study of influential areas: the creators of Game of Thrones as high fantasy creative contributors, the context of Game of Thrones -

GAME of THRONES Itinerary Leaving Belfast and Heading North, Cairncastle Is Your Destination and We’Re Right Back to the Very First Episode
The Cushendun Caves GAME OF THRONES itinerary Leaving Belfast and heading north, Cairncastle is your destination and we’re right back to the very first episode. This three-day itinerary brings you right into It was here that Ned Stark took his long-sword Ice and the bloody heart of the Seven Kingdoms. struck off the head of a Night’s Watch deserter, as John, Along the route, we’ll pass through the most Bran, Rob and Theon looked on. Heading west from memorable locations from the show, where Cairncastle, the Shillanavogy Valley is your next stop. This was where the ferocious Dothraki hoard set up camp, and the wicked Lannisters, honourable Starks the verdant, green valley was seamlessly transformed and all the rest play out their parts. into the swaying grasslands of Vaes Dothrak. The journey continues to Glenariff Forest Park taking you to the Fight practice ground at Runestone, seat of House Royce in the So sharpen your sword, tighten your shield- Vale of Arryn which is located east of the Eyrie, on the strap and set forth on a journey into the real coast of the Narrow Sea. You will recall that Robin Arryn world Westeros. has been sent to Runestone, where Royce's men are training him to use a sword under the watchful eye of Littlefinger, Sansa Stark and Yohn Royce. Head north east towards Antrim’s stunning coastline: the Cushendun Caves are calling. Davos Seaworth acted against his better judgment when he escorted Lady Melisandre on her quest to assassinate Renly Baratheon. We travel from this small seaside town to explore several The Cushendun Caves were used for the unforgettable more Game of Thrones settings. -

Narrative Structure of a Song of Ice and Fire Creates a Fictional World
Narrative structure of A Song of Ice and Fire creates a fictional world with realistic measures of social complexity Thomas Gessey-Jonesa , Colm Connaughtonb,c , Robin Dunbard , Ralph Kennae,f,1 ,Padraig´ MacCarrong,h, Cathal O’Conchobhaire , and Joseph Yosee,f aFitzwilliam College, University of Cambridge, Cambridge CB3 0DG, United Kingdom; bMathematics Institute, University of Warwick, Coventry CV4 7AL, United Kingdom; cLondon Mathematical Laboratory, London W6 8RH, United Kingdom; dDepartment of Experimental Psychology, University of Oxford, e f 4 Oxford OX2 6GG, United Kingdom; Centre for Fluid and Complex Systems, Coventry University, Coventry CV1 5FB, United Kingdom; L Collaboration, Institute for Condensed Matter Physics of the National Academy of Sciences of Ukraine, 79011 Lviv, Ukraine; gMathematics Applications Consortium for Science and Industry, Department of Mathematics & Statistics, University of Limerick, Limerick V94 T9PX, Ireland; and hCentre for Social Issues Research, University of Limerick, Limerick V94 T9PX, Ireland Edited by Kenneth W. Wachter, University of California, Berkeley, CA, and approved September 15, 2020 (received for review April 6, 2020) Network science and data analytics are used to quantify static and Schklovsky and Propp (11) and developed by Metz, Chatman, dynamic structures in George R. R. Martin’s epic novels, A Song of Genette, and others (12–14). Ice and Fire, works noted for their scale and complexity. By track- Graph theory has been used to compare character networks ing the network of character interactions as the story unfolds, it to real social networks (15) in mythological (16), Shakespearean is found that structural properties remain approximately stable (17), and fictional literature (18). To investigate the success of Ice and comparable to real-world social networks.