11. Graph Theory Def: V:Non-Empty Vertexornode Set E ⊆ V ×V :Edge Set G ≡ (V, E):Directed Graph on V, Or Digraph on V
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Analyzing Social Media Network for Students in Presidential Election 2019 with Nodexl
ANALYZING SOCIAL MEDIA NETWORK FOR STUDENTS IN PRESIDENTIAL ELECTION 2019 WITH NODEXL Irwan Dwi Arianto Doctoral Candidate of Communication Sciences, Airlangga University Corresponding Authors: [email protected] Abstract. Twitter is widely used in digital political campaigns. Twitter as a social media that is useful for building networks and even connecting political participants with the community. Indonesia will get a demographic bonus starting next year until 2030. The number of productive ages that will become a demographic bonus if not recognized correctly can be a problem. The election organizer must seize this opportunity for the benefit of voter participation. This study aims to describe the network structure of students in the 2019 presidential election. The first debate was held on January 17, 2019 as a starting point for data retrieval on Twitter social media. This study uses data sources derived from Twitter talks from 17 January 2019 to 20 August 2019 with keywords “#pilpres2019 OR #mahasiswa since: 2019-01-17”. The data obtained were analyzed by the communication network analysis method using NodeXL software. Our Analysis found that Top Influencer is @jokowi, as well as Top, Mentioned also @jokowi while Top Tweeters @okezonenews and Top Replied-To @hasmi_bakhtiar. Jokowi is incumbent running for re-election with Ma’ruf Amin (Senior Muslim Cleric) as his running mate against Prabowo Subianto (a former general) and Sandiaga Uno as his running mate (former vice governor). This shows that the more concentrated in the millennial generation in this case students are presidential candidates @jokowi. @okezonenews, the official twitter account of okezone.com (MNC Media Group). -

A Multigraph Approach to Social Network Analysis
1 Introduction Network data involving relational structure representing interactions between actors are commonly represented by graphs where the actors are referred to as vertices or nodes, and the relations are referred to as edges or ties connecting pairs of actors. Research on social networks is a well established branch of study and many issues concerning social network analysis can be found in Wasserman and Faust (1994), Carrington et al. (2005), Butts (2008), Frank (2009), Kolaczyk (2009), Scott and Carrington (2011), Snijders (2011), and Robins (2013). A common approach to social network analysis is to only consider binary relations, i.e. edges between pairs of vertices are either present or not. These simple graphs only consider one type of relation and exclude the possibility for self relations where a vertex is both the sender and receiver of an edge (also called edge loops or just shortly loops). In contrast, a complex graph is defined according to Wasserman and Faust (1994): If a graph contains loops and/or any pairs of nodes is adjacent via more than one line the graph is complex. [p. 146] In practice, simple graphs can be derived from complex graphs by collapsing the multiple edges into single ones and removing the loops. However, this approach discards information inherent in the original network. In order to use all available network information, we must allow for multiple relations and the possibility for loops. This leads us to the study of multigraphs which has not been treated as extensively as simple graphs in the literature. As an example, consider a network with vertices representing different branches of an organ- isation. -

Social Networking Analysis to Analyze the Function of Collaborative Care Teams in an Online Social Networking Tool
Using Social Networking Analysis to Analyze the Function of Collaborative Care Teams in an Online Social Networking Tool By William Trevor Jamieson B.Math(CS) M.D. FRCPC A CAPSTONE PROJECT Presented to the Department of Medical Informatics and Clinical Epidemiology and the Oregon Health & Sciences University School of Medicine In partial fulfillment of the requirements for the degree of Master of Biomedical Informatics December 2015 1 School of Medicine Oregon Health & Science University CERTIFICATE OF APPROVAL This is to certify that the Master’s Capstone Project of William Trevor Jamieson “USING SOCIAL NETWORKING ANALYSIS TO ANALYZE THE FUNCTION OF COLLABORATIVE CARE TEAMS IN AN ONLINE SOCIAL NETWORKING TOOL” Has been approved Michael F. Chiang, M.D. Capstone Advisor 2 ACKNOWLEDGEMENTS ............................................................................................................ 5 ABSTRACT ................................................................................................................................ 6 INTRODUCTION ....................................................................................................................... 7 LOOP – A PATIENT-CENTERED ONLINE COLLABORATION TOOL .............................................. 10 DESIGN, DEVELOPMENT AND BASIC FUNCTIONALITY OF LOOP ............................................................. 10 EVALUATION OF LOOP THROUGH A PRAGMATIC RANDOMIZED-CONTROLLED TRIAL ................................ 15 SOCIAL NETWORKING ANALYSIS – AN EVALUATION TECHNIQUE -

Assortativity Measures for Weighted and Directed Networks
Assortativity measures for weighted and directed networks Yelie Yuan1, Jun Yan1, and Panpan Zhang2,∗ 1Department of Statistics, University of Connecticut, Storrs, CT 06269 2Department of Biostatistics, Epidemiology and Informatics, University of Pennsylvania, Philadelphia, PA 19104 ∗Corresponding author: [email protected] January 15, 2021 arXiv:2101.05389v1 [stat.AP] 13 Jan 2021 Abstract Assortativity measures the tendency of a vertex in a network being connected by other ver- texes with respect to some vertex-specific features. Classical assortativity coefficients are defined for unweighted and undirected networks with respect to vertex degree. We propose a class of assortativity coefficients that capture the assortative characteristics and structure of weighted and directed networks more precisely. The vertex-to-vertex strength correlation is used as an example, but the proposed measure can be applied to any pair of vertex-specific features. The effectiveness of the proposed measure is assessed through extensive simula- tions based on prevalent random network models in comparison with existing assortativity measures. In application World Input-Ouput Networks, the new measures reveal interesting insights that would not be obtained by using existing ones. An implementation is publicly available in a R package wdnet. 1 Introduction In traditional network analysis, assortativity or assortative mixing (Newman, 2002) is a mea- sure assessing the preference of a vertex being connected (by edges) with other vertexes in a network. The measure reflects the principle of homophily (McPherson et al., 2001)|the tendency of the entities to be associated with similar partners in a social network. The prim- itive assortativity measure proposed by Newman(2002) was defined to study the tendency of connections between nodes based on their degrees, which is why it is also called degree-degree correlation (van der Hofstad and Litvak, 2014). -

Loop-Free Routing Using Diffusing Computations
130 IEEIYACM TRANSACTIONS ON NETWORKING, VOL. 1, NO, 1, FEBRUARY 1993 Loop-Free Routing Using Diffusing Computations J. J. Garcia-Lunes-Aceves, Member, IEEE Abstract-A family of distributed algorithms for the dynamic networks including the old ARPANET routing protocol [18] computation of the shortest paths in a computer network or and the NETCHANGE protocol of the MERIT network [26]. Memet is presented, validated, and analyzed. According to these Well-known examples of DVP’S implemented in intemetworks algorithms, each node maintains a vector with its distance to every other node. Update messages from a node are sent only are the Routing Information Protocol (RIP) [10], the Gateway- to its neighbors; each such message contains a dktance vector to-Gateway Protocol (GGP) [11], and the Exterior Gateway of one or more entries, and each entry specifies the length Protocol (EGP) [20]. All of these DVP’S have used variants of the selected path to a network destination, as well as m of the distributed Bellman-Ford algorithm (DBF) for shortest indication of whether the entry constitutes an update, a query, path computation [4]. The primary disadvantages of this or a reply to a previous query. The new algorithms treat the problem of distributed shortest-path routing as one of diffusing algorithm are routing-table loops and counting to infinity [13]. computations, which was firzt proposed by Dijkztra and Scholten. A routing-table loop is a path specified in the nodes’ routing They improve on algorithms introduced previously by Chandy tables at a particular point in time, such that the path visits and Misra, JatYe and Moss, Merlin and Segatl, and the author. -

PDF Reference
NetworkX Reference Release 1.0 Aric Hagberg, Dan Schult, Pieter Swart January 08, 2010 CONTENTS 1 Introduction 1 1.1 Who uses NetworkX?..........................................1 1.2 The Python programming language...................................1 1.3 Free software...............................................1 1.4 Goals...................................................1 1.5 History..................................................2 2 Overview 3 2.1 NetworkX Basics.............................................3 2.2 Nodes and Edges.............................................4 3 Graph types 9 3.1 Which graph class should I use?.....................................9 3.2 Basic graph types.............................................9 4 Operators 129 4.1 Graph Manipulation........................................... 129 4.2 Node Relabeling............................................. 134 4.3 Freezing................................................. 135 5 Algorithms 137 5.1 Boundary................................................. 137 5.2 Centrality................................................. 138 5.3 Clique.................................................. 142 5.4 Clustering................................................ 145 5.5 Cores................................................... 147 5.6 Matching................................................. 148 5.7 Isomorphism............................................... 148 5.8 PageRank................................................. 161 5.9 HITS.................................................. -

Approximating Graph Conductance: from Global to Local
APPROXIMATING GRAPH CONDUCTANCE: FROM GLOBAL TO LOCAL YUEHENG ZHANG Abstract. In this expository paper, we introduce spectral algorithms and random walk based algorithms on graphs through the problem of finding sparse cuts in both global and local settings. First, we consider the global problem of finding a set with minimum conductance, and show how the Laplacian and normalized Laplacian matrices arise naturally when we relax this problem to an eigenvalue computation problem. Then we bound the relaxed quantity, completing a spectral approximation algorithm and a proof of Cheeger's in- equality. Next, we discuss limitations of this global algorithm and motivate the problem of finding local conductance, for which we introduce random walks on graphs. We discuss how to gain information about conductance from the con- vergence of random walks, and motivate convergence bounds related to local conductance. Finally, we briefly introduce algorithms utilizing such bounds. Throughout, we place an emphasis on providing motivation and explanations from an algorithmic point of view. Contents 1. Introduction 1 1.1. Notation and general definitions 3 1.2. Conductance of cuts and of a graph 4 2. Generalized Rayleigh quotient and variational characterization of eigenvalues 5 3. Spectral approximation of the conductance of a graph 7 3.1. Relaxing the problem of finding the conductance of a graph 7 3.1.1. Cut capacity and the Laplacian 7 3.1.2. Normalized Laplacian and the easy side of Cheeger 9 3.2. Lower bounding the relaxation and the hard side of Cheeger 11 4. Local low-conductance sets and random walks on a graph 15 4.1. -
Graphs, & Networks 10 and Now!
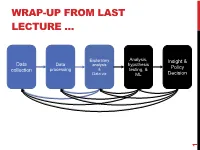
WRAP-UP FROM LAST LECTURE … Exploratory Analysis, Insight & Data Data hypothesis analysis Policy collection processing & testing, & Data viz ML Decision 1 DISCRETE TO CONTINUOUS VARIABLES Some models only work on continuous numeric data Convert a binary variable to a number ??????????? • health_insurance = {“yes”, “no”} ! {1, 0} Why not {-1, +1} or {-10, +14}? • 0/1 encoding lets us say things like “if a person has healthcare then their income increases by $X.” • Might need {-1,+1} for certain ML algorithms (e.g., SVM) 2 DISCRETE TO CONTINUOUS VARIABLES What about non-binary variables? My main transportation is a {BMW, Bicycle, Hovercraft} One option: { BMW ! 1, Bicycle ! 2, Hovercraft ! 3 } • Problems ?????????? One-hot encoding: convert a categorical variable with N values into a N-bit vector: • BMW ! [1, 0, 0]; Bicycle ! [0, 1, 0]; Hovercraft ! [0, 0, 1] # Converts dtype=category to one-hot-encoded cols cols = [‘BMW’,’Bicycle’,’Hovercraft’] df = pd.Series(cols) df = pd.get_dummies( df ) 3 CONTINUOUS TO DISCRETE VARIABLES Do doctors prescribe a certain medication to older kids more often? Is there a difference in wage based on age? Pick a discrete set of bins, then put values into the bins Equal-length bins: • Bins have an equal-length range and skewed membership • Good/Bad ???????? Equal-sized bins: • Bins have variable-length ranges but equal membership • Good/Bad ???????? 4 BIN SIZES http://www.hcbravo.org/IntroDataSci/bookdown-notes/eda-data-transformations.html 5 DIFFERENT NUMBER OF BINS https://web.ma.utexas.edu/users/mks/statmistakes/dividingcontinuousintocategories.html -

Spectrum of Laplacians for Graphs with Self-Loops
Spectrum of Laplacians for Graphs with Self-Loops Beh¸cet A¸cıkme¸se Department of Aerospace Engineering and Engineering Mechanics The University of Texas at Austin, USA June 9, 2015 Abstract This note introduces a result on the location of eigenvalues, i.e., the spectrum, of the Laplacian for a family of undirected graphs with self-loops. We extend on the known results for the spectrum of undirected graphs without self-loops or multiple edges. For this purpose, we introduce a new concept of pseudo-connected graphs and apply a lifting of the graph with self-loops to a graph without self-loops, which is then used to quantify the spectrum of the Laplacian for the graph with self-loops. 1 Introduction Graph theory has proven to be an extremely useful mathematical framework for many emerging engineering applications [1, 2, 3, 4, 5, 6]. This note introduces a result, Theorem 1, on the location of eigenvalues, i.e., the spectrum, of the Laplacian for a family of undirected graphs with self-loops. We extend on the known results for the spectrum of undirected graphs without self-loops or multiple edges [7, 8, 9]. For this purpose, we arXiv:1505.08133v2 [math.OC] 6 Jun 2015 introduce a new concept of pseudo-connected graphs and apply a lifting of the graph with self-loops to a graph without self-loops, which is then used to quantify the spectrum of the Laplacian for the graph with self-loops. The primary motivation for this result is to analyze interconnected control systems that emerge from new engineering applications such as control of multiple vehicles or spacecraft [10, 11, 12, 13, 2]. -

DEGREE ASSORTATIVITY in NETWORKS of SPIKING NEURONS 1. Introduction Our Nervous System Consists of a Vast Network of Interconnec
DEGREE ASSORTATIVITY IN NETWORKS OF SPIKING NEURONS CHRISTIAN BLASCHE,¨ SHAWN MEANS, AND CARLO R. LAING Abstract. Degree assortativity refers to the increased or decreased probability of connecting two neurons based on their in- or out-degrees, relative to what would be expected by chance. We investigate the effects of such assortativity in a network of theta neurons. The Ott/Antonsen ansatz is used to derive equations for the expected state of each neuron, and these equations are then coarse-grained in degree space. We generate families of effective connectivity matrices parametrised by assortativity coefficient and use SVD decompositions of these to efficiently perform numerical bifurcation analysis of the coarse-grained equations. We find that of the four possible types of degree assortativity, two have no effect on the networks' dynamics, while the other two can have a significant effect. 1. Introduction Our nervous system consists of a vast network of interconnected neurons. The network structure is dynamic and connections are formed or removed according to their usage. Much effort has been put into creating a map of all neuronal interconnections; a so-called brain atlas or connectome. Given such a network there are many structural features and measures that one can use to characterise it, e.g. betweenness, centrality, average path- length and clustering coefficient [27]. Obtaining these measures in actual physiological systems is challenging to say the least; nevertheless, insights into intrinsic connectivity preferences of neurons were ob- served via their growth in culture [8, 35]. Neurons with similar numbers of processes (e.g., synapses and dendrites) tend to establish links with each other { akin to socialites associating in groups and vice-versa. -

Geometric Graph Homomorphisms
1 Geometric Graph Homomorphisms Debra L. Boutin Department of Mathematics Hamilton College, Clinton, NY 13323 [email protected] Sally Cockburn Department of Mathematics Hamilton College, Clinton, NY 13323 [email protected] Abstract A geometric graph G is a simple graph drawn on points in the plane, in general position, with straightline edges. A geometric homo- morphism from G to H is a vertex map that preserves adjacencies and crossings. This work proves some basic properties of geometric homo- morphisms and defines the geochromatic number as the minimum n so that there is a geometric homomorphism from G to a geometric n-clique. The geochromatic number is related to both the chromatic number and to the minimum number of plane layers of G. By pro- viding an infinite family of bipartite geometric graphs, each of which is constructed of two plane layers, which take on all possible values of geochromatic number, we show that these relationships do not de- termine the geochromatic number. This paper also gives necessary (but not sufficient) and sufficient (but not necessary) conditions for a geometric graph to have geochromatic number at most four. As a corollary we get precise criteria for a bipartite geometric graph to have geochromatic number at most four. This paper also gives criteria for a geometric graph to be homomorphic to certain geometric realizations of K2;2 and K3;3. 1 Introduction Much work has been done studying graph homomorphisms. A graph homo- morphism f : G ! H is a vertex map that preserves adjacencies (but not necessarily non-adjacencies). If such a map exists, we write G ! H and 2 say `G is homomorphic to H.' As of this writing, there are 166 research pa- pers and books addressing graph homomorphisms. -

A Review of Geometric, Topological and Graph Theory Apparatuses for the Modeling and Analysis of Biomolecular Data
A review of geometric, topological and graph theory apparatuses for the modeling and analysis of biomolecular data Kelin Xia1 ∗and Guo-Wei Wei2;3 y 1Division of Mathematical Sciences, School of Physical and Mathematical Sciences, Nanyang Technological University, Singapore 637371 2Department of Mathematics Michigan State University, MI 48824, USA 3Department of Biochemistry & Molecular Biology Michigan State University, MI 48824, USA January 31, 2017 Abstract Geometric, topological and graph theory modeling and analysis of biomolecules are of essential im- portance in the conceptualization of molecular structure, function, dynamics, and transport. On the one hand, geometric modeling provides molecular surface and structural representation, and offers the basis for molecular visualization, which is crucial for the understanding of molecular structure and interactions. On the other hand, it bridges the gap between molecular structural data and theoretical/mathematical mod- els. Topological analysis and modeling give rise to atomic critic points and connectivity, and shed light on the intrinsic topological invariants such as independent components (atoms), rings (pockets) and cavities. Graph theory analyzes biomolecular interactions and reveals biomolecular structure-function relationship. In this paper, we review certain geometric, topological and graph theory apparatuses for biomolecular data modeling and analysis. These apparatuses are categorized into discrete and continuous ones. For discrete approaches, graph theory, Gaussian network model, anisotropic network model, normal mode analysis, quasi-harmonic analysis, flexibility and rigidity index, molecular nonlinear dynamics, spectral graph the- ory, and persistent homology are discussed. For continuous mathematical tools, we present discrete to continuum mapping, high dimensional persistent homology, biomolecular geometric modeling, differential geometry theory of surfaces, curvature evaluation, variational derivation of minimal molecular surfaces, atoms in molecule theory and quantum chemical topology.