Direct to SOM
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Type-Safe Composition of Object Modules*
International Conference on Computer Systems and Education I ISc Bangalore Typ esafe Comp osition of Ob ject Mo dules Guruduth Banavar Gary Lindstrom Douglas Orr Department of Computer Science University of Utah Salt LakeCity Utah USA Abstract Intro duction It is widely agreed that strong typing in We describ e a facility that enables routine creases the reliability and eciency of soft typ echecking during the linkage of exter ware However compilers for statically typ ed nal declarations and denitions of separately languages suchasC and C in tradi compiled programs in ANSI C The primary tional nonintegrated programming environ advantage of our serverstyle typ echecked ments guarantee complete typ esafety only linkage facility is the ability to program the within a compilation unit but not across comp osition of ob ject mo dules via a suite of suchunits Longstanding and widely avail strongly typ ed mo dule combination op era able linkers comp ose separately compiled tors Such programmability enables one to units bymatching symb ols purely byname easily incorp orate programmerdened data equivalence with no regard to their typ es format conversion stubs at linktime In ad Such common denominator linkers accom dition our linkage facility is able to automat mo date ob ject mo dules from various source ically generate safe co ercion stubs for com languages by simply ignoring the static se patible encapsulated data mantics of the language Moreover com monly used ob ject le formats are not de signed to incorp orate source language typ e -

Faster Ffts in Medium Precision
Faster FFTs in medium precision Joris van der Hoevena, Grégoire Lecerfb Laboratoire d’informatique, UMR 7161 CNRS Campus de l’École polytechnique 1, rue Honoré d’Estienne d’Orves Bâtiment Alan Turing, CS35003 91120 Palaiseau a. Email: [email protected] b. Email: [email protected] November 10, 2014 In this paper, we present new algorithms for the computation of fast Fourier transforms over complex numbers for “medium” precisions, typically in the range from 100 until 400 bits. On the one hand, such precisions are usually not supported by hardware. On the other hand, asymptotically fast algorithms for multiple precision arithmetic do not pay off yet. The main idea behind our algorithms is to develop efficient vectorial multiple precision fixed point arithmetic, capable of exploiting SIMD instructions in modern processors. Keywords: floating point arithmetic, quadruple precision, complexity bound, FFT, SIMD A.C.M. subject classification: G.1.0 Computer-arithmetic A.M.S. subject classification: 65Y04, 65T50, 68W30 1. Introduction Multiple precision arithmetic [4] is crucial in areas such as computer algebra and cryptography, and increasingly useful in mathematical physics and numerical analysis [2]. Early multiple preci- sion libraries appeared in the seventies [3], and nowadays GMP [11] and MPFR [8] are typically very efficient for large precisions of more than, say, 1000 bits. However, for precisions which are only a few times larger than the machine precision, these libraries suffer from a large overhead. For instance, the MPFR library for arbitrary precision and IEEE-style standardized floating point arithmetic is typically about a factor 100 slower than double precision machine arithmetic. -

GNU MPFR the Multiple Precision Floating-Point Reliable Library Edition 4.1.0 July 2020
GNU MPFR The Multiple Precision Floating-Point Reliable Library Edition 4.1.0 July 2020 The MPFR team [email protected] This manual documents how to install and use the Multiple Precision Floating-Point Reliable Library, version 4.1.0. Copyright 1991, 1993-2020 Free Software Foundation, Inc. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version published by the Free Software Foundation; with no Invariant Sections, with no Front-Cover Texts, and with no Back- Cover Texts. A copy of the license is included in Appendix A [GNU Free Documentation License], page 59. i Table of Contents MPFR Copying Conditions ::::::::::::::::::::::::::::::::::::::: 1 1 Introduction to MPFR :::::::::::::::::::::::::::::::::::::::: 2 1.1 How to Use This Manual::::::::::::::::::::::::::::::::::::::::::::::::::::::::::: 2 2 Installing MPFR ::::::::::::::::::::::::::::::::::::::::::::::: 3 2.1 How to Install ::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::: 3 2.2 Other `make' Targets :::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::: 4 2.3 Build Problems :::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::: 4 2.4 Getting the Latest Version of MPFR ::::::::::::::::::::::::::::::::::::::::::::::: 4 3 Reporting Bugs::::::::::::::::::::::::::::::::::::::::::::::::: 5 4 MPFR Basics ::::::::::::::::::::::::::::::::::::::::::::::::::: 6 4.1 Headers and Libraries :::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::: 6 -

IEEE Standard 754 for Binary Floating-Point Arithmetic
Work in Progress: Lecture Notes on the Status of IEEE 754 October 1, 1997 3:36 am Lecture Notes on the Status of IEEE Standard 754 for Binary Floating-Point Arithmetic Prof. W. Kahan Elect. Eng. & Computer Science University of California Berkeley CA 94720-1776 Introduction: Twenty years ago anarchy threatened floating-point arithmetic. Over a dozen commercially significant arithmetics boasted diverse wordsizes, precisions, rounding procedures and over/underflow behaviors, and more were in the works. “Portable” software intended to reconcile that numerical diversity had become unbearably costly to develop. Thirteen years ago, when IEEE 754 became official, major microprocessor manufacturers had already adopted it despite the challenge it posed to implementors. With unprecedented altruism, hardware designers had risen to its challenge in the belief that they would ease and encourage a vast burgeoning of numerical software. They did succeed to a considerable extent. Anyway, rounding anomalies that preoccupied all of us in the 1970s afflict only CRAY X-MPs — J90s now. Now atrophy threatens features of IEEE 754 caught in a vicious circle: Those features lack support in programming languages and compilers, so those features are mishandled and/or practically unusable, so those features are little known and less in demand, and so those features lack support in programming languages and compilers. To help break that circle, those features are discussed in these notes under the following headings: Representable Numbers, Normal and Subnormal, Infinite -

Effectiveness of Floating-Point Precision on the Numerical Approximation by Spectral Methods
Mathematical and Computational Applications Article Effectiveness of Floating-Point Precision on the Numerical Approximation by Spectral Methods José A. O. Matos 1,2,† and Paulo B. Vasconcelos 1,2,∗,† 1 Center of Mathematics, University of Porto, R. Dr. Roberto Frias, 4200-464 Porto, Portugal; [email protected] 2 Faculty of Economics, University of Porto, R. Dr. Roberto Frias, 4200-464 Porto, Portugal * Correspondence: [email protected] † These authors contributed equally to this work. Abstract: With the fast advances in computational sciences, there is a need for more accurate compu- tations, especially in large-scale solutions of differential problems and long-term simulations. Amid the many numerical approaches to solving differential problems, including both local and global methods, spectral methods can offer greater accuracy. The downside is that spectral methods often require high-order polynomial approximations, which brings numerical instability issues to the prob- lem resolution. In particular, large condition numbers associated with the large operational matrices, prevent stable algorithms from working within machine precision. Software-based solutions that implement arbitrary precision arithmetic are available and should be explored to obtain higher accu- racy when needed, even with the higher computing time cost associated. In this work, experimental results on the computation of approximate solutions of differential problems via spectral methods are detailed with recourse to quadruple precision arithmetic. Variable precision arithmetic was used in Tau Toolbox, a mathematical software package to solve integro-differential problems via the spectral Tau method. Citation: Matos, J.A.O.; Vasconcelos, Keywords: floating-point arithmetic; variable precision arithmetic; IEEE 754-2008 standard; quadru- P.B. -
C Language Features
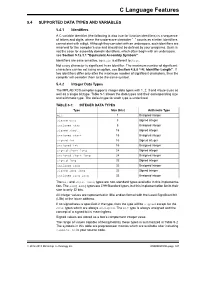
C Language Features 5.4 SUPPORTED DATA TYPES AND VARIABLES 5.4.1 Identifiers A C variable identifier (the following is also true for function identifiers) is a sequence of letters and digits, where the underscore character “_” counts as a letter. Identifiers cannot start with a digit. Although they can start with an underscore, such identifiers are reserved for the compiler’s use and should not be defined by your programs. Such is not the case for assembly domain identifiers, which often begin with an underscore, see Section 5.12.3.1 “Equivalent Assembly Symbols”. Identifiers are case sensitive, so main is different to Main. Not every character is significant in an identifier. The maximum number of significant characters can be set using an option, see Section 4.8.8 “-N: Identifier Length”. If two identifiers differ only after the maximum number of significant characters, then the compiler will consider them to be the same symbol. 5.4.2 Integer Data Types The MPLAB XC8 compiler supports integer data types with 1, 2, 3 and 4 byte sizes as well as a single bit type. Table 5-1 shows the data types and their corresponding size and arithmetic type. The default type for each type is underlined. TABLE 5-1: INTEGER DATA TYPES Type Size (bits) Arithmetic Type bit 1 Unsigned integer signed char 8 Signed integer unsigned char 8 Unsigned integer signed short 16 Signed integer unsigned short 16 Unsigned integer signed int 16 Signed integer unsigned int 16 Unsigned integer signed short long 24 Signed integer unsigned short long 24 Unsigned integer signed long 32 Signed integer unsigned long 32 Unsigned integer signed long long 32 Signed integer unsigned long long 32 Unsigned integer The bit and short long types are non-standard types available in this implementa- tion. -

Static Reflection
N3996- Static reflection Document number: N3996 Date: 2014-05-26 Project: Programming Language C++, SG7, Reflection Reply-to: Mat´uˇsChochl´ık([email protected]) Static reflection How to read this document The first two sections are devoted to the introduction to reflection and reflective programming, they contain some motivational examples and some experiences with usage of a library-based reflection utility. These can be skipped if you are knowledgeable about reflection. Section3 contains the rationale for the design decisions. The most important part is the technical specification in section4, the impact on the standard is discussed in section5, the issues that need to be resolved are listed in section7, and section6 mentions some implementation hints. Contents 1. Introduction4 2. Motivation and Scope6 2.1. Usefullness of reflection............................6 2.2. Motivational examples.............................7 2.2.1. Factory generator............................7 3. Design Decisions 11 3.1. Desired features................................. 11 3.2. Layered approach and extensibility...................... 11 3.2.1. Basic metaobjects........................... 12 3.2.2. Mirror.................................. 12 3.2.3. Puddle.................................. 12 3.2.4. Rubber................................. 13 3.2.5. Lagoon................................. 13 3.3. Class generators................................ 14 3.4. Compile-time vs. Run-time reflection..................... 16 4. Technical Specifications 16 4.1. Metaobject Concepts............................. -

Names for Standardized Floating-Point Formats
Names WORK IN PROGRESS April 19, 2002 11:05 am Names for Standardized Floating-Point Formats Abstract I lack the courage to impose names upon floating-point formats of diverse widths, precisions, ranges and radices, fearing the damage that can be done to one’s progeny by saddling them with ill-chosen names. Still, we need at least a list of the things we must name; otherwise how can we discuss them without talking at cross-purposes? These things include ... Wordsize, Width, Precision, Range, Radix, … all of which must be both declarable by a computer programmer, and ascertainable by a program through Environmental Inquiries. And precision must be subject to truncation by Coercions. Conventional Floating-Point Formats Among the names I have seen in use for floating-point formats are … float, double, long double, real, REAL*…, SINGLE PRECISION, DOUBLE PRECISION, double extended, doubled double, TEMPREAL, quad, … . Of these floating-point formats the conventional ones include finite numbers x all of the form x = (–1)s·m·ßn+1–P in which s, m, ß, n and P are integers with the following significance: s is the Sign bit, 0 or 1 according as x ≥ 0 or x ≤ 0 . ß is the Radix or Base, two for Binary and ten for Decimal. (I exclude all others). P is the Precision measured in Significant Digits of the given radix. m is the Significand or Coefficient or (wrongly) Mantissa of | x | running in the range 0 ≤ m ≤ ßP–1 . ≤ ≤ n is the Exponent, perhaps Biased, confined to some interval Nmin n Nmax . Other terms are in use. -

COS 217: Introduction to Programming Systems
COS 217: Introduction to Programming Systems Crash Course in C (Part 2) The Design of C Language Features and Data Types and their Operations and Representations @photoshobby INTEGERS 43 Integer Data Types Integer types of various sizes: {signed, unsigned} {char, short, int, long} • char is 1 byte • Number of bits per byte is unspecified! (but in the 21st century, safe to assume it’s 8) • Sizes of other integer types not fully specified but constrained: • int was intended to be “natural word size” of hardware • 2 ≤ sizeof(short) ≤ sizeof(int) ≤ sizeof(long) On ArmLab: • Natural word size: 8 bytes (“64-bit machine”) • char: 1 byte • short: 2 bytes • int: 4 bytes (compatibility with widespread 32-bit code) • long: 8 bytes What decisions did the 44 designers of Java make? Integer Literals • Decimal int: 123 • Octal int: 0173 = 123 • Hexadecimal int: 0x7B = 123 • Use "L" suffix to indicate long literal • No suffix to indicate char-sized or short integer literals; instead, cast Examples • int: 123, 0173, 0x7B • long: 123L, 0173L, 0x7BL • short: (short)123, (short)0173, (short)0x7B Unsigned Integer Data Types unsigned types: unsigned char, unsigned short, unsigned int, and unsigned long • Hold only non-negative integers Default for short, int, long is signed • char is system dependent (on armlab char is unsigned) • Use "U" suffix to indicate unsigned literal Examples • unsigned int: • 123U, 0173U, 0x7BU • Oftentimes the U is omitted for small values: 123, 0173, 0x7B • (Technically there is an implicit cast from signed to unsigned, but in these -

Static Reflection
N4451- Static reflection (rev. 3) Document number: N4451 Date: 2015-04-11 Project: Programming Language C++, SG7, Reflection Reply-to: Mat´uˇsChochl´ık([email protected]) Static reflection (rev. 3) Mat´uˇsChochl´ık Abstract This paper is the follow-up to N3996 and N4111 an it is the third revision of the proposal to add support for static reflection to the C++ standard. During the presentation of N4111 concerns were expressed about the level-of-detail and scope of the presented proposal and possible dangers of giving non-expert language users a too powerful tool to use and the dangers of implementing it all at once. This paper aims to address these issues. Furthermore, the accompanying paper { N4452 describes several use cases of reflection, which were called for during the presentation of N4111. Contents 1. Introduction5 2. Design preferences5 2.1. Consistency...................................5 2.2. Reusability...................................5 2.3. Flexibility....................................6 2.4. Encapsulation..................................6 2.5. Stratification..................................6 2.6. Ontological correspondence..........................6 2.7. Completeness..................................6 2.8. Ease of use...................................6 2.9. Cooperation with rest of the standard and other librares..........6 2.10. Extensibility..................................7 3. Currently proposed metaobject concepts7 3.1. Categorization and Traits...........................8 3.1.1. Metaobject category tags.......................8 3.2. StringConstant.................................9 3.3. Metaobject Sequence.............................. 10 3.3.1. size ................................... 11 1 N4451- Static reflection (rev. 3) 3.3.2. at .................................... 11 3.3.3. for each ................................ 12 3.4. Metaobject................................... 12 3.4.1. is metaobject ............................. 13 3.4.2. metaobject category ......................... 14 3.4.3. Traits.................................. 14 3.4.4. -

Chapter 6 Data Types
Chapter 6 Data Types • Introduction • Type Nomenclature • Primitive Types • Type constructors – Ordinal Types – Structured Types • Type Checking • Type conversion CSCI325 Chapter 6 Dr Ahmed Rafea 1 Introduction Evolution of Data Types: FORTRAN I (1956) - INTEGER, REAL, arrays … Ada (1983) - User can create a unique type for every category of variables in the problem space and have the system enforce the types Def: A descriptor is the collection of the attributes of a variable Def: A data type is a set of values, together with a set of operations on those values having certain properties CSCI325 Chapter 6 Dr Ahmed Rafea 2 Type Nomenclature C Types Basic Derived Void Numeric Pointer Array Function struct union Integral Floating Float (signed) enum Double (unsigned) Long double char Int Short int Long int CSCI325 Chapter 6 Dr Ahmed Rafea 3 Primitive Data Types Integer - Almost always an exact reflection of the hardware, so the mapping is trivial - There may be as many as eight different integer types in a language Floating Point - Model real numbers, but only as approximations - Languages for scientific use support at least two floating-point types; sometimes more - Usually exactly like the hardware, but not always; Decimal - For business applications (money) - Store a fixed number of decimal digits (coded) - Advantage: accuracy - Disadvantages: limited range, wastes memory Boolean - Could be implemented as bits, but often as bytes - Advantage: readability CSCI325 Chapter 6 Dr Ahmed Rafea 4 Ordinal Types (user defined) An ordinal type is one in which the range of possible values can be easily associated with the set of positive integers 1. -

Codewarrior Development Studio for Starcore 3900FP Dsps Application Binary Interface (ABI) Reference Manual
CodeWarrior Development Studio for StarCore 3900FP DSPs Application Binary Interface (ABI) Reference Manual Document Number: CWSCABIREF Rev. 10.9.0, 06/2015 CodeWarrior Development Studio for StarCore 3900FP DSPs Application Binary Interface (ABI) Reference Manual, Rev. 10.9.0, 06/2015 2 Freescale Semiconductor, Inc. Contents Section number Title Page Chapter 1 Introduction 1.1 Standards Covered............................................................................................................................................................ 7 1.2 Accompanying Documentation........................................................................................................................................ 8 1.3 Conventions...................................................................................................................................................................... 8 1.3.1 Numbering Systems............................................................................................................................................. 8 1.3.2 Typographic Notation.......................................................................................................................................... 9 1.3.3 Special Terms.......................................................................................................................................................9 Chapter 2 Low-level Binary Interface 2.1 StarCore Architectures......................................................................................................................................................11