GPU Acceleration of the Variational Monte Carlo Method for Many Body
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Wu Washington 0250E 15755.Pdf (3.086Mb)
© Copyright 2016 Sang Wu Contributions to Physics-Based Aeroservoelastic Uncertainty Analysis Sang Wu A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy University of Washington 2016 Reading Committee: Eli Livne, Chair Mehran Mesbahi Dorothy Reed Frode Engelsen Program Authorized to Offer Degree: Aeronautics and Astronautics University of Washington Abstract Contributions to Physics-Based Aeroservoelastic Uncertainty Analysis Sang Wu Chair of the Supervisory Committee: Professor Eli Livne The William E. Boeing Department of Aeronautics and Astronautics The thesis presents the development of a new fully-integrated, MATLAB based simulation capability for aeroservoelastic (ASE) uncertainty analysis that accounts for uncertainties in all disciplines as well as discipline interactions. This new capability allows probabilistic studies of complex configuration at a scope and with depth not known before. Several statistical tools and methods have been integrated into the capability to guide the tasks such as parameter prioritization, uncertainty reduction, and risk mitigation. The first task of the thesis focuses on aeroservoelastic uncertainty assessment considering control component uncertainty. The simulation has shown that attention has to be paid, if notch filters are used in the aeroservoelastic loop, to the variability and uncertainties of the aircraft involved. The second task introduces two innovative methodologies to characterize the unsteady aerodynamic uncertainty. One is a physically based aerodynamic influence coefficients element by element correction uncertainty scheme and the other is an alternative approach focusing on rational function approximation matrix uncertainties to evaluate the relative impact of uncertainty in aerodynamic stiffness, damping, inertia, or lag terms. Finally, the capability has been applied to obtain the gust load response statistics accounting for uncertainties in both aircraft and gust profiles. -

Analysing Census at School Data
Analysing Census At School Data www.censusatschool.ie Project Maths Development Team 2015 Page 1 of 7 Excel for Analysing Census At School Data Having retrieved a class’s data using CensusAtSchool: 1. Save the downloaded class data which is a .csv file as an .xls file. 2. Delete any unwanted variables such as the teacher name, date stamp etc. 3. Freeze the top row so that one can scroll down to view all of the data while the top row remains in view. 4. Select certain columns (not necessarily contiguous) for use as a class worksheet. Aim to have a selection of categorical data (nominal and ordered) and numerical data (discrete and continuous) unless one requires one type exclusively. The number of columns will depend on the class as too much data might be intimidating for less experienced classes. Students will need to have the questionnaire to hand to identify the question which produced the data. 5. Make a new worksheet within the workbook of downloaded data using the selected columns. 6. Name the worksheet i.e. “data for year 2 2014” or “data for margin of error investigation”. 7. Format the data to show all borders (useful if one is going to make a selection of the data and put it into Word). 8. Order selected columns of this data perhaps (and use expand selection) so that rogue data such as 0 for height etc. can be eliminated. It is perhaps useful for students to see this. (Use Sort & Filter.) 9. Use a filter on data, for example based on gender, to generate further worksheets for future use 10. -

A Monte Carlo Simulation Approach to the Reliability Modeling of the Beam Permit System of Relativistic Heavy Ion Collider (Rhic) at Bnl* P
Proceedings of ICALEPCS2013, San Francisco, CA, USA MOPPC075 A MONTE CARLO SIMULATION APPROACH TO THE RELIABILITY MODELING OF THE BEAM PERMIT SYSTEM OF RELATIVISTIC HEAVY ION COLLIDER (RHIC) AT BNL* P. Chitnis#, T.G. Robertazzi, Stony Brook University, Stony Brook, NY 11790, U.S.A. K.A. Brown, Brookhaven National Laboratory, Upton, NY 11973, U.S.A. Abstract called the Permit Carrier Link, Blue Carrier Link and The RHIC Beam Permit System (BPS) monitors the Yellow Carrier link. These links carry 10 MHz signals health of RHIC subsystems and takes active decisions whose presence allows the beam in the ring. Support regarding beam-abort and magnet power dump, upon a systems report their status to BPS through “Input subsystem fault. The reliability of BPS directly impacts triggers” called Permit Inputs (PI) and Quench Inputs the RHIC downtime, and hence its availability. This work (QI). If any support system PI fails, the permit carrier assesses the probability of BPS failures that could lead to terminates, initiating a beam dump. If QI fails, then the substantial downtime. A fail-safe condition imparts blue and yellow carriers also terminate, initiating magnet downtime to restart the machine, while a failure to power dump in blue and yellow ring magnets. The carrier respond to an actual fault can cause potential machine failure propagates around the ring to inform other PMs damage and impose significant downtime. This paper about the occurrence of a fault. illustrates a modular multistate reliability model of the Other than PMs, BPS also has 4 Abort Kicker Modules BPS, with modules having exponential lifetime (AKM) that see the permit carrier failure and send the distributions. -
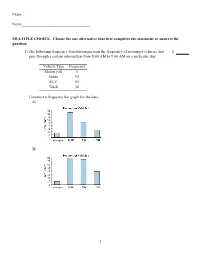
2 3 Practice Problems.Pdf
Exam Name___________________________________ MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. 1) The following frequency distribution presents the frequency of passenger vehicles that 1) pass through a certain intersection from 8:00 AM to 9:00 AM on a particular day. Vehicle Type Frequency Motorcycle 5 Sedan 95 SUV 65 Truck 30 Construct a frequency bar graph for the data. A) B) 1 C) D) 2) The following bar graph presents the average amount a certain family spent, in dollars, on 2) various food categories in a recent year. On which food category was the most money spent? A) Dairy products B) Cereals and baked goods C) Fruits and vegetables D) Meat poultry, fish, eggs 3) The following frequency distribution presents the frequency of passenger vehicles that 3) pass through a certain intersection from 8:00 AM to 9:00 AM on a particular day. Vehicle Type Frequency Motorcycle 9 Sedan 54 SUV 27 2 Truck 53 Construct a relative frequency bar graph for the data. A) B) C) D) 3 4) The following frequency distribution presents the frequency of passenger vehicles that 4) pass through a certain intersection from 8:00 AM to 9:00 AM on a particular day. Vehicle Type Frequency Motorcycle 9 Sedan 20 SUV 25 Truck 39 Construct a pie chart for the data. A) B) C) D) 5) The following pie chart presents the percentages of fish caught in each of four ratings 5) categories. Match this pie chart with its corresponding Parato chart. 4 A) B) C) 5 D) SHORT ANSWER. -

Type Here Title of the Paper
ICME 11, TSG 13, Monterrey, Mexico, 2008: Dave Pratt Shaping the Experience of Young and Naïve Probabilists Pratt, Dave Institute of Education, University of London. [email protected] Summary This paper starts by briefly summarizing research which has focused on student misconceptions with respect to understanding probability, before outlining the author’s research, which, in contrast, presents what students of age 11-12 years(Grade 7) do know and can construct, given access to a carefully designed environment. These students judged randomness according to unpredictability, lack of pattern in results, lack of control over outcomes and fairness. In many respects their judgments were based on similar characteristics to those of experts. However, it was only through interaction with a virtual environment, ChanceMaker, that the students began to express situated meanings for aggregated long-term randomness. That data is then re-analyzed in order to reflect upon the design decisions that shaped the environment itself. Four main design heuristics are identified and elaborated: Testing personal conjectures, Building on student knowledge, Linking purpose and utility, Fusing control and representation. In conclusion, it is conjectured that these heuristics are of wider relevance to teachers and lecturers, who aspire to shape the experience of young and naïve probabilists through their actions as designers of tasks and pedagogical settings. Preamble The aim in this paper is to propose heuristics that might usefully guide design decisions for pedagogues, who might be building software, creating new curriculum approaches, imagining a novel task or writing a lesson plan. (Here I use the term “heuristics” with its standard meaning as a rule-of-thumb, a guiding rule, rather than in the specialized sense that has been adopted by researchers of judgments of chance.) With this aim in mind, I re-analyze data that have previously informed my research on students’ meanings for randomness as emergent during activity. -

Revisiting the Sustainable Happiness Model and Pie Chart: Can Happiness Be Successfully Pursued?
The Journal of Positive Psychology Dedicated to furthering research and promoting good practice ISSN: 1743-9760 (Print) 1743-9779 (Online) Journal homepage: https://www.tandfonline.com/loi/rpos20 Revisiting the Sustainable Happiness Model and Pie Chart: Can Happiness Be Successfully Pursued? Kennon M. Sheldon & Sonja Lyubomirsky To cite this article: Kennon M. Sheldon & Sonja Lyubomirsky (2019): Revisiting the Sustainable Happiness Model and Pie Chart: Can Happiness Be Successfully Pursued?, The Journal of Positive Psychology, DOI: 10.1080/17439760.2019.1689421 To link to this article: https://doi.org/10.1080/17439760.2019.1689421 Published online: 07 Nov 2019. Submit your article to this journal View related articles View Crossmark data Full Terms & Conditions of access and use can be found at https://www.tandfonline.com/action/journalInformation?journalCode=rpos20 THE JOURNAL OF POSITIVE PSYCHOLOGY https://doi.org/10.1080/17439760.2019.1689421 Revisiting the Sustainable Happiness Model and Pie Chart: Can Happiness Be Successfully Pursued? Kennon M. Sheldona,b and Sonja Lyubomirskyc aUniversity of Missouri, Columbia, MO, USA; bNational Research University Higher School of Economics, Moscow, Russian Federation; cUniversity of California, Riverside, CA, USA ABSTRACT ARTICLE HISTORY The Sustainable Happiness Model (SHM) has been influential in positive psychology and well-being Received 4 September 2019 science. However, the ‘pie chart’ aspect of the model has received valid critiques. In this article, we Accepted 8 October 2019 start by agreeing with many such critiques, while also explaining the context of the original article KEYWORDS and noting that we were speculative but not dogmatic therein. We also show that subsequent Subjective well-being; research has supported the most important premise of the SHM – namely, that individuals can sustainable happiness boost their well-being via their intentional behaviors, and maintain that boost in the longer-term. -

Doing More with SAS/ASSIST® 9.1 the Correct Bibliographic Citation for This Manual Is As Follows: SAS Institute Inc
Doing More With SAS/ASSIST® 9.1 The correct bibliographic citation for this manual is as follows: SAS Institute Inc. 2004. Doing More With SAS/ASSIST ® 9.1. Cary, NC: SAS Institute Inc. Doing More With SAS/ASSIST® 9.1 Copyright © 2004, SAS Institute Inc., Cary, NC, USA ISBN 1-59047-206-3 All rights reserved. Produced in the United States of America. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, or otherwise, without the prior written permission of the publisher, SAS Institute Inc. U.S. Government Restricted Rights Notice. Use, duplication, or disclosure of this software and related documentation by the U.S. government is subject to the Agreement with SAS Institute and the restrictions set forth in FAR 52.227–19 Commercial Computer Software-Restricted Rights (June 1987). SAS Institute Inc., SAS Campus Drive, Cary, North Carolina 27513. 1st printing, January 2004 SAS Publishing provides a complete selection of books and electronic products to help customers use SAS software to its fullest potential. For more information about our e-books, e-learning products, CDs, and hard-copy books, visit the SAS Publishing Web site at support.sas.com/publishing or call 1-800-727-3228. SAS® and all other SAS Institute Inc. product or service names are registered trademarks or trademarks of SAS Institute Inc. in the USA and other countries. ® indicates USA registration. Other brand and product names are registered trademarks or trademarks of -

Miro Correlates with Other Psychometrics 13 Your Miro Practitioner 14
YOUR MIRO REPORT Adam Smith MiRo Behavioural Mode Assessment Table of Contents What does this report tell me? 3 The MiRo Behaviours Mode Summary Model 5 Your MiRo Behavioural Results 6 MiRo Correlates With Other Psychometrics 13 Your MiRo practitioner 14 Page 2 of 14 © MiRo Psychometrics Ltd 2015 What does this report tell me? Your personality is a particular pattern of behaviour and thinking prevailing across time and situations that differentiates one person from another. It is made up of many different elements, some innate, some learned. Apart from our inherited traits we develop ways of being and doing based on all kinds of good and bad experiences, value decisions and external influences. This complex system of attributes, behavioural temperament, emotions and mental energies is impossible to fully comprehend, let alone assess and quantify. Therefore the MiRo system looks at what can be observed, such as our habitual behaviours. These behaviours are determined by how we unconsciously perceive our environment and ourselves in relation to that environment. By measuring behaviour psychologists and psychotherapists such as William Marston and Carl Jung have indentified four main Behavioural Modes that are open to all of us. MiRo refers to these Modes as Driving, Energising, Organising and analysing and we use these Modes in order of our own preferences. Page 3 of 14 © MiRo Psychometrics Ltd 2015 The order of preference in which these behaviours are used is as follows: • Leading Behaviour which determines your main Behavioural traits • Supporting Behaviour which will act as a backup Behaviour to your Leading Behaviour • Supplementary Behaviourwhich can act to enhance your overall Behaviour • Dormant Behaviour which will be the Behaviour that you ignore Your MiRo results are based on the answers that you gave in your assessment, which is deliberately designed to force response based on habit and instinct. -

Statistical Graphics Considerations January 7, 2020
Statistical Graphics Considerations January 7, 2020 https://opr.princeton.edu/workshops/65 Instructor: Dawn Koffman, Statistical Programmer Office of Population Research (OPR) Princeton University 1 Statistical Graphics Considerations Why this topic? “Most of us use a computer to write, but we would never characterize a Nobel prize winning writer as being highly skilled at using a word processing tool. Similarly, advanced skills with graphing languages/packages/tools won’t necessarily lead to effective communication of numerical data. You must understand the principles of effective graphs in addition to the mechanics.” Jennifer Bryan, Associate Professor Statistics & Michael Smith Labs, Univ. of British Columbia. http://stat545‐ubc.github.io/block015_graph‐dos‐donts.html 2 “... quantitative visualization is a core feature of scientific practice from start to finish. All aspects of the research process from the initial exploration of data to the effective presentation of a polished argument can benefit from good graphical habits. ... the dominant trend is toward a world where the visualization of data and results is a routine part of what it means to do science.” But ... for some odd reason “ ... the standards for publishable graphical material vary wildy between and even within articles – far more than the standards for data analysis, prose and argument. Variation is to be expected, but the absence of consistency in elements as simple as axis labeling, gridlines or legends is striking.” 3 Kieran Healy and James Moody, Data Visualization in Sociology, Annu. Rev. Sociol. 2014 40:5.1‐5.5. What is a statistical graph? “A statistical graph is a visual representation of statistical data. -

No Humble Pie: the Origins and Usage of a Statistical Chart
Journal of Educational and Behavioral Statistics Winter 2005, Vol. 30, No. 4, pp. 353–368 No Humble Pie: The Origins and Usage of a Statistical Chart Ian Spence University of Toronto William Playfair’s pie chart is more than 200 years old and yet its intellectual ori- gins remain obscure. The inspiration likely derived from the logic diagrams of Llull, Bruno, Leibniz, and Euler, which were familiar to William because of the instruction of his mathematician brother John. The pie chart is broadly popular but—despite its common appeal—most experts have not been seduced, and the academy has advised avoidance; nonetheless, the masses have chosen to ignore this advice. This commentary discusses the origins of the pie chart and the appro- priate uses of the form. Keywords: Bruno, circle chart, Euler, Leibniz, Llull, logic diagrams, pie chart, Playfair 1. Introduction The pie chart is more than two centuries old. The diagram first appeared (Playfair, 1801) as an element of two larger graphical displays (see Figure 1 for one instance) in The Statistical Breviary, whose charts portrayed the areas, populations, and rev- enues of European states. William Playfair had previously devised the bar chart and was first to advocate and popularize the use of the line graph to display time series in statistics (Playfair, 1786). The pie chart was his last major graphical invention. Playfair was an accomplished and talented adapter of the ideas of others, and although we may be confident that we know his sources of inspiration in the case of the bar chart and line graph, the intellectual motivations for the pie chart and its parent, the circle chart, remain obscure. -

A Guide to Using Data for Health Care Quality Improvement
A guide to using data for health care quality improvement June 2008 Published by the Rural and Regional Health and Aged Care Services Division, Victorian Government Department of Human Services, Melbourne, Victoria. June 2008 This booklet is available in pdf format and may be downloaded from the VQC website at www.health.vic.gov.au/qualitycouncil © Copyright State of Victoria, Department of Human Services, 2008 This publication is copyright. No part may be reproduced by any process except in accordance with the provisions of the Copyright Act 1968 Authorised by the Victorian Government, 50 Lonsdale St., Melbourne 3000. Printed by Big Print, 50 Lonsdale St, Melbourne VIC 3000. rcc_080507 Victorian Quality Council Secretariat Phone 1300 135 427 Email [email protected] Website www.health.vic.gov.au/qualitycouncil A GUIDE TO USING DATA FOR HEALTH CARE QUALITY IMPROVEMENT This resource has been developed for the Victorian Quality Council by: Project Health Fiona Landgren, author Jessie Murray, research and documentation Its development has been overseen by a reference group comprising: Victorian Quality Council members Associate Professor Caroline Brand, Chair (Clinical Epidemiology and Health Service Evaluation Unit, Melbourne Health) (Centre for Research Excellence in Patient Safety) Ms Kerry Bradley (Mary MacKillop Aged Care) Dr Peter McDougall (Royal Children’s Hospital) Associate Professor Les Reti (The Royal Women’s Hospital) External experts Dr Chris Bain (The Western and Central Melbourne Integrated Cancer Service) Ms Anna Donne (Department -

Redesigning Google Form Responses
Redesigning Google Form Responses Sage Isabella Stanford University [email protected] Abstract 2 Related Work This project was motivated by personal struggles with Taking a simplistic design and updating it to better fit user Google Forms, a free service provided by Google for form needs is becoming a more common practice in the data creation, sharing, and reviewing, but with limited tools for visualization field. A popularly cited article renovates hotel exploratory data analysis. These struggles prompted the organization methods by researching what managers question: What interactions can be designed that improve physically tracked, updating those features to a digital data analysis that fit well with Google’s simple to use interface, and using the new platform to create insightful interface? This question was explored by reviewing prior interactions [Weaver, Fyfe, Robinson, Holdsworth, Peuquet, visualization research, collecting an online survey to gauge Maceachren 2006]. Redesigning Google Form Responses use and satisfaction, ideating on possible solutions, uses similar methodology to design a new interface that generating three video prototypes (chart filter, highlighting assists and not overwhelms current users. table, and drag to combine), interviewing current Google Forms users on prototypes, and collecting survey data on Several platforms already exist for form creation with prototypes. It was found that clicking on aspects of charts to varying features for data visualization. (See Table 1) filter the Summary of Responses and highlight entries in Google Sheets was intuitive and useful to most users. Table 1: Top Online Form Building Platforms Dragging charts to combine data was a conceptual leap, but useful to some. Name Public Price Analysis Features 1 Introduction Survey 1999 $0-$85 - Filter Monkey monthly - Crosstab There are hundreds of form platforms online, but arguably - Word Clouds/Text none as accessible as Google Forms.