Edge Guarding Plane Graphs
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Independence Number, Vertex (Edge) ୋ Cover Number and the Least Eigenvalue of a Graph
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Linear Algebra and its Applications 433 (2010) 790–795 Contents lists available at ScienceDirect Linear Algebra and its Applications journal homepage: www.elsevier.com/locate/laa The vertex (edge) independence number, vertex (edge) ୋ cover number and the least eigenvalue of a graph ∗ Ying-Ying Tan a, Yi-Zheng Fan b, a Department of Mathematics and Physics, Anhui University of Architecture, Hefei 230601, PR China b School of Mathematical Sciences, Anhui University, Hefei 230039, PR China ARTICLE INFO ABSTRACT Article history: In this paper we characterize the unique graph whose least eigen- Received 4 October 2009 value attains the minimum among all graphs of a fixed order and Accepted 4 April 2010 a given vertex (edge) independence number or vertex (edge) cover Available online 8 May 2010 number, and get some bounds for the vertex (edge) independence Submitted by X. Zhan number, vertex (edge) cover number of a graph in terms of the least eigenvalue of the graph. © 2010 Elsevier Inc. All rights reserved. AMS classification: 05C50 15A18 Keywords: Graph Adjacency matrix Vertex (edge) independence number Vertex (edge) cover number Least eigenvalue 1. Introduction Let G = (V,E) be a simple graph of order n with vertex set V = V(G) ={v1,v2, ...,vn} and edge set E = E(G). The adjacency matrix of G is defined to be a (0, 1)-matrix A(G) =[aij], where aij = 1ifvi is adjacent to vj and aij = 0 otherwise. The eigenvalues of the graph G are referred to the eigenvalues of A(G), which are arranged as λ1(G) λ2(G) ··· λn(G). -

3.1 Matchings and Factors: Matchings and Covers
1 3.1 Matchings and Factors: Matchings and Covers This copyrighted material is taken from Introduction to Graph Theory, 2nd Ed., by Doug West; and is not for further distribution beyond this course. These slides will be stored in a limited-access location on an IIT server and are not for distribution or use beyond Math 454/553. 2 Matchings 3.1.1 Definition A matching in a graph G is a set of non-loop edges with no shared endpoints. The vertices incident to the edges of a matching M are saturated by M (M-saturated); the others are unsaturated (M-unsaturated). A perfect matching in a graph is a matching that saturates every vertex. perfect matching M-unsaturated M-saturated M Contains copyrighted material from Introduction to Graph Theory by Doug West, 2nd Ed. Not for distribution beyond IIT’s Math 454/553. 3 Perfect Matchings in Complete Bipartite Graphs a 1 The perfect matchings in a complete b 2 X,Y-bigraph with |X|=|Y| exactly c 3 correspond to the bijections d 4 f: X -> Y e 5 Therefore Kn,n has n! perfect f 6 matchings. g 7 Kn,n The complete graph Kn has a perfect matching iff… Contains copyrighted material from Introduction to Graph Theory by Doug West, 2nd Ed. Not for distribution beyond IIT’s Math 454/553. 4 Perfect Matchings in Complete Graphs The complete graph Kn has a perfect matching iff n is even. So instead of Kn consider K2n. We count the perfect matchings in K2n by: (1) Selecting a vertex v (e.g., with the highest label) one choice u v (2) Selecting a vertex u to match to v K2n-2 2n-1 choices (3) Selecting a perfect matching on the rest of the vertices. -

Catalogue of Graph Polynomials
Catalogue of graph polynomials J.A. Makowsky April 6, 2011 Contents 1 Graph polynomials 3 1.1 Comparinggraphpolynomials. ........ 3 1.1.1 Distinctivepower.............................. .... 3 1.1.2 Substitutioninstances . ...... 4 1.1.3 Uniformalgebraicreductions . ....... 4 1.1.4 Substitutioninstances . ...... 4 1.1.5 Substitutioninstances . ...... 4 1.1.6 Substitutioninstances . ...... 4 1.2 Definabilityofgraphpolynomials . ......... 4 1.2.1 Staticdefinitions ............................... ... 4 1.2.2 Dynamicdefinitions .............................. 4 1.2.3 SOL-definablepolynomials ............................ 4 1.2.4 Generalizedchromaticpolynomials . ......... 4 2 A catalogue of graph polynomials 5 2.1 Polynomialsfromthezoo . ...... 5 2.1.1 Chromaticpolynomial . .... 5 2.1.2 Chromatic symmetric function . ...... 6 2.1.3 Adjointpolynomials . .... 6 2.1.4 TheTuttepolynomial . ... 7 2.1.5 Strong Tutte symmetric function . ....... 7 2.1.6 Tutte-Grothendieck invariants . ........ 8 2.1.7 Aweightedgraphpolynomial . ..... 8 2.1.8 Chainpolynomial ............................... 9 2.1.9 Characteristicpolynomial . ....... 10 2.1.10 Matchingpolynomial. ..... 11 2.1.11 Theindependentsetpolynomial . ....... 12 2.1.12 Thecliquepolynomial . ..... 14 2.1.13 Thevertex-coverpolynomial . ...... 14 2.1.14 Theedge-coverpolynomial . ..... 15 2.1.15 TheMartinpolynomial . 16 2.1.16 Interlacepolynomial . ...... 17 2.1.17 Thecoverpolynomial . 19 2.1.18 Gopolynomial ................................. 21 2.1.19 Stabilitypolynomial . ...... 23 1 2.1.20 Strong U-polynomial............................... -

IEOR 269, Spring 2010 Integer Programming and Combinatorial Optimization
IEOR 269, Spring 2010 Integer Programming and Combinatorial Optimization Professor Dorit S. Hochbaum Contents 1 Introduction 1 2 Formulation of some ILP 2 2.1 0-1 knapsack problem . 2 2.2 Assignment problem . 2 3 Non-linear Objective functions 4 3.1 Production problem with set-up costs . 4 3.2 Piecewise linear cost function . 5 3.3 Piecewise linear convex cost function . 6 3.4 Disjunctive constraints . 7 4 Some famous combinatorial problems 7 4.1 Max clique problem . 7 4.2 SAT (satisfiability) . 7 4.3 Vertex cover problem . 7 5 General optimization 8 6 Neighborhood 8 6.1 Exact neighborhood . 8 7 Complexity of algorithms 9 7.1 Finding the maximum element . 9 7.2 0-1 knapsack . 9 7.3 Linear systems . 10 7.4 Linear Programming . 11 8 Some interesting IP formulations 12 8.1 The fixed cost plant location problem . 12 8.2 Minimum/maximum spanning tree (MST) . 12 9 The Minimum Spanning Tree (MST) Problem 13 i IEOR269 notes, Prof. Hochbaum, 2010 ii 10 General Matching Problem 14 10.1 Maximum Matching Problem in Bipartite Graphs . 14 10.2 Maximum Matching Problem in Non-Bipartite Graphs . 15 10.3 Constraint Matrix Analysis for Matching Problems . 16 11 Traveling Salesperson Problem (TSP) 17 11.1 IP Formulation for TSP . 17 12 Discussion of LP-Formulation for MST 18 13 Branch-and-Bound 20 13.1 The Branch-and-Bound technique . 20 13.2 Other Branch-and-Bound techniques . 22 14 Basic graph definitions 23 15 Complexity analysis 24 15.1 Measuring quality of an algorithm . -

New Approximation Algorithms for Minimum Weighted Edge Cover
New Approximation Algorithms for Minimum Weighted Edge Cover S M Ferdous∗ Alex Potheny Arif Khanz Abstract The K-Nearest Neighbor graph is used to spar- We describe two new 3=2-approximation algorithms and a sify data sets, which is an important step in graph-based new 2-approximation algorithm for the minimum weight semi-supervised machine learning. Here one has a few edge cover problem in graphs. We show that one of the 3=2-approximation algorithms, the Dual Cover algorithm, labeled items, many unlabeled items, and a measure of computes the lowest weight edge cover relative to previously similarity between pairs of items; we are required to known algorithms as well as the new algorithms reported label the remaining items. A popular approach for clas- here. The Dual Cover algorithm can also be implemented to be faster than the other 3=2-approximation algorithms on sification is to generate a similarity graph between the serial computers. Many of these algorithms can be extended items to represent both the labeled and unlabeled data, to solve the b-Edge Cover problem as well. We show the and then to use a label propagation algorithm to classify relation of these algorithms to the K-Nearest Neighbor graph construction in semi-supervised learning and other the unlabeled items [23]. In this approach one builds applications. a complete graph out of the dataset and then sparsi- fies this graph by computing a K-Nearest Neighbor 1 Introduction graph [22]. This sparsification leads to efficient al- An Edge Cover in a graph is a subgraph such that gorithms, but also helps remove noise which can af- every vertex has at least one edge incident on it in fect label propagation [11]. -

Vertex and Edge Covers with Clustering Properties: Complexity and Algorithms∗
Vertex and Edge Covers with Clustering Properties: Complexity and Algorithms∗ Henning Fernau1;y and David F. Manlove2;z 1 FB IV|Abteilung Informatik, Universit¨at Trier, 54286 Trier, Germany 2 Department of Computing Science, University of Glasgow, Glasgow G12 8QQ, UK Abstract We consider the concepts of a t-total vertex cover and a t-total edge cover (t 1), which generalise the notions of a vertex cover and an edge cover, respectively. ≥A t- total vertex (respectively edge) cover of a connected graph G is a vertex (edge) cover S of G such that each connected component of the subgraph of G induced by S has at least t vertices (edges). These definitions are motivated by combining the concepts of clustering and covering in graphs. Moreover they yield a spectrum of parameters that essentially range from a vertex cover to a connected vertex cover (in the vertex case) and from an edge cover to a spanning tree (in the edge case). For various values of t, we present -completeness and approximability results (both upper and lower bounds) and N Palgorithms for problems concerned with finding the minimum size of a t-total vertexFPT cover, t-total edge cover and connected vertex cover, in particular improving on a previous algorithm for the latter problem. FPT 1 Introduction In graph theory, the notion of covering vertices or edges of graphs by other vertices or edges has been extensively studied (see [35] for a survey). For instance, covering vertices by other vertices leads to parameters concerned with vertex domination [30, 31]. When edges are to be covered by vertices we obtain parameters connected with the classical vertex covering problem [29, p.94]. -

On the Approximability of a Geometric Set Cover Problem
Electronic Colloquium on Computational Complexity, Report No. 19 (2011) On the Approximability of a Geometric Set Cover Problem Valentin E. Brimkov1, Andrew Leach2,JimmyWu2, and Michael Mastroianni2 1 Mathematics Department, SUNY Buffalo State College, Buffalo, NY 14222, USA 2 Mathematics Department, University at Buffalo, Buffalo, NY 1426-2900, USA Abstract. Given a finite set of straight line segments S in R2 and some k ∈ N, is there a subset V of points on segments in S with |V |≤k such that each segment of S contains at least one point in V ? This is a special case of the set covering problem where the family of subsets given can be taken as a set of intersections of the straight line segments in S. Requiring that the given subsets can be interpreted geometrically this way is a major restriction on the input, yet we have shown that the problem is still strongly NP-complete. In light of this result, we studied the performance of two polynomial-time approximation algorithms which return segment coverings. We obtain certain theoretical results, and in particular we show that the performance ratio for each of these algorithms is unbounded, in general. Keyword: guarding set of segments, set cover, vertex cover, approximation algorithm, worst case perfor- mance 1 Introduction Given a finite set of straight line segments, we wish to find a minimum number of points so that every segment contains at least one chosen point. Consider any physical structure that can be modeled by a finite set of straight line segments. Some examples could be a network of streets in a city, tunnels in a mine, corridors in a building or pipes in a factory. -

Approximability of Packing and Covering Problems
Approximability of Packing and Covering Problems ATHESIS SUBMITTED IN PARTIAL FULFILMENT OF THE REQUIREMENTS FOR THE DEGREE OF Master of Technology IN Faculty of Engineering BY Arka Ray Computer Science and Automation Indian Institute of Science Bangalore – 560 012 (INDIA) June, 2021 Declaration of Originality I, Arka Ray, with SR No. 04-04-00-10-42-19-1-16844 hereby declare that the material presented in the thesis titled Approximability of Packing and Covering Problems represents original work carried out by me in the Department of Computer Science and Automation at Indian Institute of Science during the years 2019-2021. With my signature, I certify that: • I have not manipulated any of the data or results. • Ihavenotcommittedanyplagiarismofintellectualproperty.Ihaveclearlyindicatedand referenced the contributions of others. • Ihaveexplicitlyacknowledgedallcollaborativeresearchanddiscussions. • Ihaveunderstoodthatanyfalseclaimwillresultinseveredisciplinaryaction. • I have understood that the work may be screened for any form of academic misconduct. Date: Student Signature In my capacity as supervisor of the above-mentioned work, I certify that the above statements are true to the best of my knowledge, and I have carried out due diligence to ensure the originality of the thesis. etmindamthan 26 06 Advisor Name: Arindam Khan Advisor Signature2021 a © Arka Ray June, 2021 All rights reserved DEDICATED TO Ma and Baba for believing in me Acknowledgements My sincerest gratitude to Arindam Khan, who, despite the gloom and doom situation of the present times, kept me motivated through his constant encouragement while tolerating my idiosyncrasies. I would also like to thank him for introducing me to approximation algorithms, along with Anand Louis, in general, and approximation of packing and covering problems in particular. -
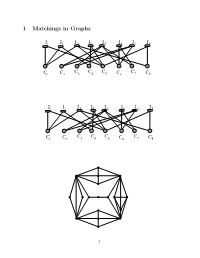
1 Matchings in Graphs
1 Matchings in Graphs JJ1 2 J 3 J4J 5 JJJ67 8 C C C C C1 C2 3 4 5 C6 7 C8 JJ1 2 J 3 J4J 5 JJJ67 8 C C C C C1 C2 3 4 5 C6 7 C8 1 Definition 1 Two edges are called independent if they are not adjacent in the graph. A set of mutually independent edges is called a matching. A matching is called maximal if no other matching contains it. maximum if its cardinality is maximal among all matchings perfect if every vertex of the graph is incident to an edge of the matching. maximal vs maximum How to construct a maximal matching? 2 Given a matching M in G, a path is called M-alternating if its edges are alternatively in M and not in M. a vertex x is called weak if no edge of M is incident to x. Using alternating path connecting weak vertices 3 The symmetric difference of two sets X and Y is the set of all ele- ments that belong to one but not the other of the sets. X ⊗ Y = (X ∪ Y ) − (X ∩ Y ) Theorem 1 A matching M is maximum iff there exists no al- ternating path between any two distinct weak vertices of G. Proof. For a proof, we will try to answer the following questions: • If a graph M is a matching, what is the maximum degree of a vertex in such a graph? • If the edge set E of a graph F is the symmetric difference of two matchings M1 and M2, then what is the maximal vertex degree of F ? • Consider a component C of F above. -

On the Triangle Clique Cover and $ K T $ Clique Cover Problems
On the Triangle Clique Cover and Kt Clique Cover Problems Hoang Dau Olgica Milenkovic Gregory J. Puleo Abstract An edge clique cover of a graph is a set of cliques that covers all edges of the graph. We generalize this concept to Kt clique cover, i.e. a set of cliques that covers all complete subgraphs on t vertices of the graph, for every t ≥ 1. In particular, we extend a classical result of Erd¨os,Goodman, and P´osa(1966) on the edge clique cover number (t = 2), also known as the intersection number, to the case t = 3. The upper bound is tight, with equality holding only for the Tur´angraph T (n; 3). As part of the proof, we obtain new upper bounds on the classical intersection number, which may be of independent interest. We also extend an algorithm of Scheinerman and Trenk (1999) to solve a weighted version of the Kt clique cover problem on a superclass of chordal graphs. We also prove that the Kt clique cover problem is NP-hard. 1 Introduction A clique in a graph G is a set of vertices that induces a complete subgraph; all graphs considered in this paper are simple and undirected. A vertex clique cover of a graph G is a set of cliques in G that collectively cover all of its vertices. The vertex clique cover number of G, denoted θv(G), is the minimum number of cliques in a vertex clique cover of G. An edge clique cover of a graph G is a set of cliques of G that collectively cover all of its edges. -

Hardness of Covering All the Triangles
Hardness of covering all the triangles Thinh D. Nguyen∗ Moscow State University [email protected] July 17, 2018 Abstract Vertex Cover and Edge Cover are two classical examples that are often used to show the contrast of problem solvability. While Vertex Cover is hard, Edge Cover can be solved in polynomial time. We claim that the former remains intractable even if the objects to be covered are triangles instead of edges. Therefore, one more combinatorial optimization problem, namely Covering Triangles, is added to the decades-old list of the problems in this research area. I. Definitions and sketch of proof If G = (V, E) is a given graph, HG is a graph which has all of the vertices and edges of G, and also for each edge of G like e = (x, y), HG has a new vertex which is connected to both x and y. A triangle is a complete graph with 3 vertices, also denoted K3. Our goal is to prove that the problem of finding the minimum number of vertices to cover all the triangles in a given graph G is NP-complete. It is worth mentioning that: (i) the Vertex Cover problem asks for a vertex cover that covers all edges, (ii) our problem Covering Triangles problem also asks for a vertex cover but the covered objects are triangles, not edges. Hence, we call our problem Covering Triangle to avoid misleading notation. Sketch of Proof: We reduce from Vertex Cover of triangle-free cubic graph, Guruswami et al. prove the hardness of this problem in [2]. -

I. Matchings and Coverings
I. Matchings and coverings 1. Matchings, covers, and Gallai’s theorem Let G = (V,E) be a graph.1 A stable set is a subset C of V such that e 6⊆ C for each edge e of G. A vertex cover is a subset W of V such that e ∩ W 6= ∅ for each edge e of G. It is not difficult to show that for each U ⊆ V : (1) U is a stable set ⇐⇒ V \ U is a vertex cover. A matching is a subset M of E such that e∩e′ = ∅ for all e, e′ ∈ M with e 6= e′. A matching 1 is called perfect if it covers all vertices (that is, has size 2 |V |). An edge cover is a subset F of E such that for each vertex v there exists e ∈ F satisfying v ∈ e. Note that an edge cover can exist only if G has no isolated vertices. Define: (2) α(G) := max{|C|| C is a stable set}, τ(G) := min{|W || W is a vertex cover}, ν(G) := max{|M|| M is a matching}, ρ(G) := min{|F || F is an edge cover}. These numbers are called the stable set number, the vertex cover number, the matching number, and the edge cover number of G, respectively. It is not difficult to show that: (3) α(G) ≤ ρ(G) and ν(G) ≤ τ(G). The triangle K3 shows that strict inequalities are possible. In fact, equality in one of the relations (3) implies equality in the other, as Gallai [6,7] proved: Theorem 1 (Gallai’s theorem).