DOCSLIB.ORG

Floquet Quantum Criticality

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Floquet Quantum Criticality Floquet quantum criticality William Berdaniera,1, Michael Kolodrubetza,b,c, S. A. Parameswarand,2, and Romain Vasseure aDepartment of Physics, University of California, Berkeley, CA 94720; bMaterials Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720; cDepartment of Physics, The University of Texas at Dallas, Richardson, TX 75080; dThe Rudolf Peierls Centre for Theoretical Physics, University of Oxford, Oxford OX1 3PU, United Kingdom; and eDepartment of Physics, University of Massachusetts, Amherst, MA 01003 Edited by David A. Huse, Princeton University, Princeton, NJ, and approved August 3, 2018 (received for review April 4, 2018) We study transitions between distinct phases of one-dimensional Our approach relies on the presence of quenched disorder, periodically driven (Floquet) systems. We argue that these are which is required for a generic periodically driven system to generically controlled by infinite-randomness fixed points of a have Floquet phase structure rather than thermalize to a feature- strong-disorder renormalization group procedure. Working in less infinite-temperature state (37–40). We argue that transitions the fermionic representation of the prototypical Floquet Ising between distinct one-dimensional Floquet phases are then best chain, we leverage infinite randomness physics to provide a described in terms of an infinite-randomness fixed point (IRFP) simple description of Floquet (multi)criticality in terms of a dis- accessed via a strong-disorder real space renormalization group tinct type of domain wall associated with time translational (RSRG) procedure. In the nonequilibrium setting, the stabil- symmetry-breaking and the formation of “Floquet time crystals.” ity of IRFPs against thermalization via long-range resonances We validate our analysis via numerical simulations of free-fermion remains a topic of debate (41–43). However, even if unstable, models sufficient to capture the critical physics. we expect that they will control the dynamics of prethermaliza- tion relevant to all reasonably accessible experimental timescales quantum criticality j disordered systems j many-body localization j (44, 45). periodically driven systems j nonperturbative arguments The universality of our analysis turns on the fact that, in the vicinity of such infinite-randomness critical points, a typical con- figuration of the system can be viewed as being composed of he assignment of robust phase structure to periodically domains deep in one of two proximate phases (46–51). Transi- driven quantum many-body systems is among the most strik- T tions that do not involve TTSB (i.e., the SG/PM or 0πPM/πSG ing results in the study of nonequilibrium dynamics (1). There transitions) map to the static (random) Ising critical point and has been dramatic progress in understanding such “Floquet” can be understood in similar terms. In contrast, transitions that systems, ranging from proposals to engineer new states of mat- involve the onset of TTSB in the bulk (PM to πSG) or at the ter via the drive (2–12) to the classification of driven analogs boundary (SG to 0πPM) can be understood in terms of a class of symmetry-protected topological phases (“Floquet SPTs”) of domain wall (DW) special to driven systems that separate (13–20). These typically require that the system under inves- regions driven at a frequency primarily near 0 or near π—a pic- tigation possess one or more microscopic global symmetries. ture we verify numerically. When the Ising model is rewritten In addition, all Floquet systems share an invariance under as a fermion problem, this picture yields a simple description of time translations by an integer multiple of their drive period. Floquet criticality in terms of DWs that bind Majorana states at Unlike the continuous time translational symmetry characteristic quasienergy 0 or π, allowing us to further study the multicritical of undriven Hamiltonian systems (21–23), this discrete sym- point where all four phases meet. metry may be spontaneously broken, leading to a distinctive dynamical response at rational fractions of the drive period— a phenomenon dubbed “time crystallinity” (24–29). The time Significance translation symmetry breaking (TTSB) exhibited by Floquet time crystals is stable against perturbations that preserve the peri- Periodically driven “Floquet” systems are nonequilibrium sys- odicity of the drive, permitting generalizations of notions such tems whose time translation symmetry can give rise to a as broken symmetry and phase rigidity to the temporal set- rich dynamical phase structure. In the presence of quenched ting. Experiments have begun to probe these predictions in disorder, they can avoid thermalizing to a bland infinite tem- well-isolated systems such as ultracold gases, ion traps (30), perature state through a phenomenon known as many-body nitrogen-vacancy centers in diamond (31), and even spatially localization (MBL). The ability of these driven MBL phases ordered crystals (32, 33). to host phenomena forbidden in equilibrium, such as “time In light of these developments, it is desirable to construct crystallinity,” has gained widespread interest in recent years. a theory of Floquet (multi)critical points between distinct In this work, we consider the question of the criticality that Floquet phases. Ideally, this should emerge as the fixed point of a emerges at the transitions between distinct Floquet MBL coarse-graining/renormalization group (RG) procedure; enable phases. By providing a universally applicable picture and us to identify critical degrees of freedom, especially those respon- applying it to a prototypical driven system, the driven Ising sible for TTSB; and allow us to compute the critical scaling chain, we identify critical points and give an understanding of behavior. Floquet criticality in general. Here, we develop such a theory for a prototypical Floquet system: the driven random quantum Ising chain. Extensive anal- Author contributions: W.B., M.K., S.A.P., and R.V. designed research, performed research, ysis has shown that this model hosts four phases (1, 24). Two contributed new reagents/analytic tools, analyzed data, and wrote the paper. of these, the paramagnet (PM) and the spin glass (SG), are The authors declare no conflict of interest. present already in the static problem (34–36). A third, the π This article is a PNAS Direct Submission. SG/time crystal, has spatiotemporal long-range order and sub- Published under the PNAS license. harmonic bulk response at half-integer multiples of the drive 1 To whom correspondence should be addressed. Email: [email protected] frequency. This phase and its Ising dual—the 0π PM, which also 2 On leave from: Department of Physics and Astronomy, University of California, Irvine, exhibits TTSB but only at the boundaries of a finite sample— CA 92697.y are unique to the driven setting. A precise understanding of This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10. PHYSICS the (multi)critical points between these distinct Floquet phases 1073/pnas.1805796115/-/DCSupplemental. accessed by tuning drive parameters is the subject of this work. Published online August 29, 2018. www.pnas.org/cgi/doi/10.1073/pnas.1805796115 PNAS j September 18, 2018 j vol. 115 j no. 38 j 9491–9496 Downloaded by guest on September 25, 2021 Model Floquet systems are defined by a time-periodic Hamiltonian H (t) = H (t + T ). For reasons similar to Bloch’s theorem, eigen- −iEαt states satisfy j α(t) = e jφα(t) , where jφα(t + T ) = jφα(t) , and we set ~ = 1 (52, 53). In contrast to the case of static Hamiltonians, the quasienergies Eα are only defined modulo 2π=T , voiding the notion of a “ground state.” An object of fundamental interest is the single-period evo- lution operator or Floquet operator F ≡ U (T ). If disorder is strong enough, F can have an extensive set of local con- served quantities. This implies area-law scaling of entangle- ment in Floquet eigenstates and consequently the absence of thermalization (54). Unlike generic (thermalizing) Floquet systems, such many- body localized (MBL) Floquet systems retain a notion of phase structure to infinitely long times. For concreteness, we focus on the driven quantum Ising chain, the simplest Floquet system that Fig. 1. Phase diagram deduced by fitting “effective central charge” from entanglement scaling (see Fig. 3 for details). (Insets) Sketches of infinite- hosts uniquely dynamical phases. The corresponding Floquet randomness coupling distributions along the critical lines (1–4) and at the operator is multicritical point (5). −i T P J σz σz +U σz σz −i T P h σx +U σx σx F = e 2 i i i i+1 i i+2 e 2 i i i i i+1 , [1] Eq. 1. The transformations Jj 7! Jj + π and hj 7! hj + π both α separately map F onto another interacting Ising-like Floquet where σ are Pauli operators. Here Ji and hi are uncorre- i SI Appendix lated random variables, and U corresponds to small interaction operator with precisely the same eigenstates ( ), but possibly distinct quasienergies: Jj 7! Jj + π preserves F exactly terms that respect the Z2 symmetry of the model generated Q x (up to boundary terms), while hj 7! hj + π sends F 7! FGIsing = by GIsing = i σi . For specificity, we draw couplings h, J ran- h,J GIsingF . Note that, despite not changing bulk properties of the domly with probability nπ from a box distribution of maxi- eigenstates, these transformations map the PM to the 0πPM and mal width about π—namely, [π=2, 3π=2]—and with probability π y h,J h,J the SG to the SG. Additionally, a global rotation about the n0 = 1 − nπ from a box distribution of maximal width about axis takes hj 7! −hj . Below, we fix phase transition lines by com- 0—namely, [−π=2, π=2]. The reasons for this parametrization bining these Floquet symmetries with the usual Ising bond-field will become evident below.
Load more

Recommended publications
  • Topological Order in Physics
    The Himalayan Physics Vol. 6 & 7, April 2017 (108-111) ISSN 2542-2545 Topological Order in Physics Ravi Karki Department of Physics, Prithvi Narayan Campus, Pokhara Email: [email protected] Abstract : In general, we know that there are four states of matter solid, liquid, gas and plasma. But there are much more states of matter. For e. g. there are ferromagnetic states of matter as revealed by the phenomenon of magnetization and superfluid states defined by the phenomenon of zero viscosity. The various phases in our colorful world are so rich that it is amazing that they can be understood systematically by the symmetry breaking theory of Landau. Topological phenomena define the topological order at macroscopic level. Topological order need new mathematical framework to describe it. More recently it is found that at microscopic level topological order is due to the long range quantum entanglement, just like the fermions fluid is due to the fermion-pair condensation. Long range quantum entanglement leads to many amazing emergent phenomena, such as fractional quantum numbers, non- Abelian statistics ad perfect conducting boundary channels. It can even provide a unified origin of light and electron i.e. gauge interactions and Fermi statistics. Light waves (gauge fields) are fluctuations of long range entanglement and electron (fermion) are defect of long range entanglements. Keywords: Topological order, degeneracy, Landau-symmetry, chiral spin state, string-net condensation, quantum glassiness, chern number, non-abelian statistics, fractional statistics. 1. INTRODUCTION 2. BACKGROUND In physics, topological order is a kind of order in zero- Although all matter is formed by atoms , matter can have temperature phase of matter also known as quantum matter.
    [Show full text]
  • 1-Crystal Symmetry and Classification-1.Pdf
    R. I. Badran Solid State Physics Fundamental types of lattices and crystal symmetry Crystal symmetry: What is a symmetry operation? It is a physical operation that changes the positions of the lattice points at exactly the same places after and before the operation. In other words, it is an operation when applied to an object leaves it apparently unchanged. e.g. A translational symmetry is occurred, for example, when the function sin x has a translation through an interval x = 2 leaves it apparently unchanged. Otherwise a non-symmetric operation can be foreseen by the rotation of a rectangle through /2. There are two groups of symmetry operations represented by: a) The point groups. b) The space groups (these are a combination of point groups with translation symmetry elements). There are 230 space groups exhibited by crystals. a) When the symmetry operations in crystal lattice are applied about a lattice point, the point groups must be used. b) When the symmetry operations are performed about a point or a line in addition to symmetry operations performed by translations, these are called space group symmetry operations. Types of symmetry operations: There are five types of symmetry operations and their corresponding elements. 85 R. I. Badran Solid State Physics Note: The operation and its corresponding element are denoted by the same symbol. 1) The identity E: It consists of doing nothing. 2) Rotation Cn: It is the rotation about an axis of symmetry (which is called "element"). If the rotation through 2/n (where n is integer), and the lattice remains unchanged by this rotation, then it has an n-fold axis.
    [Show full text]
  • Arxiv:1910.10745V1 [Cond-Mat.Str-El] 23 Oct 2019 2.2 Symmetry-Protected Time Crystals
    A Brief History of Time Crystals Vedika Khemania,b,∗, Roderich Moessnerc, S. L. Sondhid aDepartment of Physics, Harvard University, Cambridge, Massachusetts 02138, USA bDepartment of Physics, Stanford University, Stanford, California 94305, USA cMax-Planck-Institut f¨urPhysik komplexer Systeme, 01187 Dresden, Germany dDepartment of Physics, Princeton University, Princeton, New Jersey 08544, USA Abstract The idea of breaking time-translation symmetry has fascinated humanity at least since ancient proposals of the per- petuum mobile. Unlike the breaking of other symmetries, such as spatial translation in a crystal or spin rotation in a magnet, time translation symmetry breaking (TTSB) has been tantalisingly elusive. We review this history up to recent developments which have shown that discrete TTSB does takes place in periodically driven (Floquet) systems in the presence of many-body localization (MBL). Such Floquet time-crystals represent a new paradigm in quantum statistical mechanics — that of an intrinsically out-of-equilibrium many-body phase of matter with no equilibrium counterpart. We include a compendium of the necessary background on the statistical mechanics of phase structure in many- body systems, before specializing to a detailed discussion of the nature, and diagnostics, of TTSB. In particular, we provide precise definitions that formalize the notion of a time-crystal as a stable, macroscopic, conservative clock — explaining both the need for a many-body system in the infinite volume limit, and for a lack of net energy absorption or dissipation. Our discussion emphasizes that TTSB in a time-crystal is accompanied by the breaking of a spatial symmetry — so that time-crystals exhibit a novel form of spatiotemporal order.
    [Show full text]
  • Nano Boubles and More … Talk
    NanoNano boublesboubles andand moremore ……Talk Jan Zaanen 1 The Hitchhikers Guide to the Scientific Universe $14.99 Amazon.com Working title: ‘no strings attached’ 2 Nano boubles Boubles = Nano = This Meeting ?? 3 Year Round X-mas Shops 4 Nano boubles 5 Nano HOAX Nanobot = Mechanical machine Mechanical machines need RIGIDITY RIGIDITY = EMERGENT = absent on nanoscale 6 Cash 7 Correlation boubles … 8 Freshly tenured … 9 Meaningful meeting Compliments to organizers: Interdisciplinary with focus and a good taste! Compliments to the speakers: Review order well executed! 10 Big Picture Correlated Cuprates, Manganites, Organics, 2-DEG MIT “Competing Phases” “Intrinsic Glassiness” Semiconductors DMS Spin Hall Specials Ruthenates (Honerkamp ?), Kondo dots, Brazovksi… 11 Cross fertilization: semiconductors to correlated Bossing experimentalists around: these semiconductor devices are ingenious!! Pushing domain walls around (Ohno) Spin transport (spin Hall, Schliemann) -- somehow great potential in correlated … Personal highlight: Mannhart, Okamoto ! Devices <=> interfaces: lots of correlated life!! 12 Cross fertilization: correlated to semiconductors Inhomogeneity !! Theorists be aware, it is elusive … Go out and have a look: STM (Koenraad, Yazdani) Good or bad for the holy grail (high Tc)?? Joe Moore: Tc can go up by having high Tc island in a low Tc sea Resistance maximum at Tc: Lesson of manganites: big peak requires large scale electronic reorganization. 13 More resistance maximum Where are the polarons in GaMnAs ??? Zarand: strong disorder, large scale stuff, but Anderson localization at high T ?? Manganites: low T degenerate Fermi-liquid to high T classical (polaron) liquid Easily picked up by Thermopower (Palstra et al 1995): S(classical liquid) = 1000 * S(Fermi liquid) 14 Competing orders First order transition + Coulomb frustration + more difficult stuff ==> (dynamical) inhomogeniety + disorder ==> glassiness 2DEG-MIT (Fogler): Wigner X-tal vs.
    [Show full text]
  • Translational Symmetry and Microscopic Constraints on Symmetry-Enriched Topological Phases: a View from the Surface
    PHYSICAL REVIEW X 6, 041068 (2016) Translational Symmetry and Microscopic Constraints on Symmetry-Enriched Topological Phases: A View from the Surface Meng Cheng,1 Michael Zaletel,1 Maissam Barkeshli,1 Ashvin Vishwanath,2 and Parsa Bonderson1 1Station Q, Microsoft Research, Santa Barbara, California 93106-6105, USA 2Department of Physics, University of California, Berkeley, California 94720, USA (Received 15 August 2016; revised manuscript received 26 November 2016; published 29 December 2016) The Lieb-Schultz-Mattis theorem and its higher-dimensional generalizations by Oshikawa and Hastings require that translationally invariant 2D spin systems with a half-integer spin per unit cell must either have a continuum of low energy excitations, spontaneously break some symmetries, or exhibit topological order with anyonic excitations. We establish a connection between these constraints and a remarkably similar set of constraints at the surface of a 3D interacting topological insulator. This, combined with recent work on symmetry-enriched topological phases with on-site unitary symmetries, enables us to develop a framework for understanding the structure of symmetry-enriched topological phases with both translational and on-site unitary symmetries, including the effective theory of symmetry defects. This framework places stringent constraints on the possible types of symmetry fractionalization that can occur in 2D systems whose unit cell contains fractional spin, fractional charge, or a projective representation of the symmetry group. As a concrete application, we determine when a topological phase must possess a “spinon” excitation, even in cases when spin rotational invariance is broken down to a discrete subgroup by the crystal structure. We also describe the phenomena of “anyonic spin-orbit coupling,” which may arise from the interplay of translational and on-site symmetries.
    [Show full text]
  • About Symmetries in Physics
    LYCEN 9754 December 1997 ABOUT SYMMETRIES IN PHYSICS Dedicated to H. Reeh and R. Stora1 Fran¸cois Gieres Institut de Physique Nucl´eaire de Lyon, IN2P3/CNRS, Universit´eClaude Bernard 43, boulevard du 11 novembre 1918, F - 69622 - Villeurbanne CEDEX Abstract. The goal of this introduction to symmetries is to present some general ideas, to outline the fundamental concepts and results of the subject and to situate a bit the following arXiv:hep-th/9712154v1 16 Dec 1997 lectures of this school. [These notes represent the write-up of a lecture presented at the fifth S´eminaire Rhodanien de Physique “Sur les Sym´etries en Physique” held at Dolomieu (France), 17-21 March 1997. Up to the appendix and the graphics, it is to be published in Symmetries in Physics, F. Gieres, M. Kibler, C. Lucchesi and O. Piguet, eds. (Editions Fronti`eres, 1998).] 1I wish to dedicate these notes to my diploma and Ph.D. supervisors H. Reeh and R. Stora who devoted a major part of their scientific work to the understanding, description and explo- ration of symmetries in physics. Contents 1 Introduction ................................................... .......1 2 Symmetries of geometric objects ...................................2 3 Symmetries of the laws of nature ..................................5 1 Geometric (space-time) symmetries .............................6 2 Internal symmetries .............................................10 3 From global to local symmetries ...............................11 4 Combining geometric and internal symmetries ...............14
    [Show full text]
  • Arxiv:1610.05737V1 [Cond-Mat.Quant-Gas] 18 Oct 2016 Different from Photon Lasers and Constitute Genuine Quantum Degenerate Macroscopic States
    Topological order and equilibrium in a condensate of exciton-polaritons Davide Caputo,1, 2 Dario Ballarini,1 Galbadrakh Dagvadorj,3 Carlos Sánchez Muñoz,4 Milena De Giorgi,1 Lorenzo Dominici,1 Kenneth West,5 Loren N. Pfeiffer,5 Giuseppe Gigli,1, 2 Fabrice P. Laussy,6 Marzena H. Szymańska,7 and Daniele Sanvitto1 1CNR NANOTEC—Institute of Nanotechnology, Via Monteroni, 73100 Lecce, Italy 2University of Salento, Via Arnesano, 73100 Lecce, Italy 3Department of Physics, University of Warwick, Coventry CV4 7AL, United Kingdom 4Departamento de Física Teórica de la Materia Condensada, Universidad Autónoma de Madrid, 28049 Madrid, Spain 5PRISM, Princeton Institute for the Science and Technology of Materials, Princeton Unviversity, Princeton, NJ 08540 6Russian Quantum Center, Novaya 100, 143025 Skolkovo, Moscow Region, Russia 7Department of Physics and Astronomy, University College London, Gower Street, London WC1E 6BT, United Kingdom We report the observation of the Berezinskii–Kosterlitz–Thouless transition for a 2D gas of exciton-polaritons, and through the joint measurement of the first-order coherence both in space and time we bring compelling evidence of a thermodynamic equilibrium phase transition in an otherwise open driven/dissipative system. This is made possible thanks to long polariton lifetimes in high-quality samples with small disorder and in a reservoir-free region far away from the excitation spot, that allow topological ordering to prevail. The observed quasi-ordered phase, characteristic for an equilibrium 2D bosonic gas, with a decay of coherence in both spatial and temporal domains with the same algebraic exponent, is reproduced with numerical solutions of stochastic dynamics, proving that the mechanism of pairing of the topological defects (vortices) is responsible for the transition to the algebraic order.
    [Show full text]
  • Subsystem Symmetry Enriched Topological Order in Three Dimensions
    PHYSICAL REVIEW RESEARCH 2, 033331 (2020) Subsystem symmetry enriched topological order in three dimensions David T. Stephen ,1,2 José Garre-Rubio ,3,4 Arpit Dua,5,6 and Dominic J. Williamson7 1Max-Planck-Institut für Quantenoptik, Hans-Kopfermann-Straße 1, 85748 Garching, Germany 2Munich Center for Quantum Science and Technology, Schellingstraße 4, 80799 München, Germany 3Departamento de Análisis Matemático y Matemática Aplicada, UCM, 28040 Madrid, Spain 4ICMAT, C/ Nicolás Cabrera, Campus de Cantoblanco, 28049 Madrid, Spain 5Department of Physics, Yale University, New Haven, Connecticut 06511, USA 6Yale Quantum Institute, Yale University, New Haven, Connecticut 06511, USA 7Stanford Institute for Theoretical Physics, Stanford University, Stanford, California 94305, USA (Received 16 April 2020; revised 27 July 2020; accepted 3 August 2020; published 28 August 2020) We introduce a model of three-dimensional (3D) topological order enriched by planar subsystem symmetries. The model is constructed starting from the 3D toric code, whose ground state can be viewed as an equal-weight superposition of two-dimensional (2D) membrane coverings. We then decorate those membranes with 2D cluster states possessing symmetry-protected topological order under linelike subsystem symmetries. This endows the decorated model with planar subsystem symmetries under which the looplike excitations of the toric code fractionalize, resulting in an extensive degeneracy per unit length of the excitation. We also show that the value of the topological entanglement entropy is larger than that of the toric code for certain bipartitions due to the subsystem symmetry enrichment. Our model can be obtained by gauging the global symmetry of a short-range entangled model which has symmetry-protected topological order coming from an interplay of global and subsystem symmetries.
    [Show full text]
  • Evidence for Singular-Phonon-Induced Nematic Superconductivity in a Topological Superconductor Candidate Sr0.1Bi2se3
    ARTICLE https://doi.org/10.1038/s41467-019-10942-2 OPEN Evidence for singular-phonon-induced nematic superconductivity in a topological superconductor candidate Sr0.1Bi2Se3 Jinghui Wang1, Kejing Ran1, Shichao Li1, Zhen Ma1, Song Bao1, Zhengwei Cai1, Youtian Zhang1, Kenji Nakajima 2, Seiko Ohira-Kawamura2,P.Čermák3,4, A. Schneidewind 3, Sergey Y. Savrasov5, Xiangang Wan1,6 & Jinsheng Wen 1,6 1234567890():,; Superconductivity mediated by phonons is typically conventional, exhibiting a momentum- independent s-wave pairing function, due to the isotropic interactions between electrons and phonons along different crystalline directions. Here, by performing inelastic neutron scat- tering measurements on a superconducting single crystal of Sr0.1Bi2Se3, a prime candidate for realizing topological superconductivity by doping the topological insulator Bi2Se3,wefind that there exist highly anisotropic phonons, with the linewidths of the acoustic phonons increasing substantially at long wavelengths, but only for those along the [001] direction. This obser- vation indicates a large and singular electron-phonon coupling at small momenta, which we propose to give rise to the exotic p-wave nematic superconducting pairing in the MxBi2Se3 (M = Cu, Sr, Nb) superconductor family. Therefore, we show these superconductors to be example systems where electron-phonon interaction can induce more exotic super- conducting pairing than the s-wave, consistent with the topological superconductivity. 1 National Laboratory of Solid State Microstructures and Department of Physics, Nanjing University, Nanjing 210093, China. 2 J-PARC Center, Japan Atomic Energy Agency, Tokai, Ibaraki 319-1195, Japan. 3 Jülich Centre for Neutron Science (JCNS) at Heinz Maier-Leibnitz Zentrum (MLZ), Forschungszentrum Jülich GmbH, Lichtenbergstr. 1, 85748 Garching, Germany.
    [Show full text]
  • Geometry, Topology, and Response in Condensed Matter Systems by Dániel Varjas a Dissertation Submitted in Partial Satisfaction
    Geometry, topology, and response in condensed matter systems by D´anielVarjas A dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in Physics in the Graduate Division of the University of California, Berkeley Committee in charge: Professor Joel E. Moore, Chair Professor Ashvin Vishwanath Professor Sayeef Salahuddin Summer 2016 Geometry, topology, and response in condensed matter systems Copyright 2016 by D´anielVarjas 1 Abstract Geometry, topology, and response in condensed matter systems by D´anielVarjas Doctor of Philosophy in Physics University of California, Berkeley Professor Joel E. Moore, Chair Topological order provides a new paradigm to view phases of matter. Unlike conven- tional symmetry breaking order, these states are not distinguished by different patterns of symmetry breaking, instead by their intricate mathematical structure, topology. By the bulk-boundary correspondence, the nontrivial topology of the bulk results in robust gap- less excitations on symmetry preserving surfaces. We utilize both of these views to study topological phases together with the analysis of their quantized physical responses to per- turbations. First we study the edge excitations of strongly interacting abelian fractional quantum Hall liquids on an infinite strip geometry. We use the infinite density matrix renormalization group method to numerically measure edge exponents in model systems, including subleading orders. Using analytic methods we derive a generalized Luttinger's theorem that relates momenta of edge excitations. Next we consider topological crystalline insulators protected by space group symme- try. After reviewing the general formalism, we present results about the quantization of the magnetoelectric response protected by orientation-reversing space group symmetries.
    [Show full text]
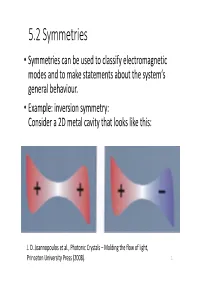
  • 5.2 Symmetries • Symmetries Can Be Used to Classify Electromagnetic Modes and to Make Statements About the System‘S General Behaviour
    5.2 Symmetries • Symmetries can be used to classify electromagnetic modes and to make statements about the system‘s general behaviour. • Example: inversion symmetry: Consider a 2D metal cavity that looks like this: J. D. Joannopoulos et al., Photonic Crystals – Molding the flow of light, Princeton University Press (2008). 1 • The shape is somewhat arbitrary, making an analytical solution difficult, but it has inversion symmetry if is a mode with frequency , then must also be a mode with frequency • Unless is a member of a degenerate family of modes, then if has the same frequency, it must be the same mode, i.e. it must be a multiple of : . • If we invert the system twice we obtain or . • A given nondegenerate mode must be of one of the two types, either it is invariant under inversion (even mode) or it becomes its own opposite (odd mode). • Thereby we have classified the modes of the system based on how they respond to one of its symmetry operations. 2 • Let‘s capture this idea in a more abstract language • Suppose is an operator (a 3x3 matrix) that inverts vectors (3x1 matrices), so that • To invert a vector field, we need an operator that inverts both the vector and ist argument : • For an inversion symmetric system it does not matter if we operate with or if we first invert the coordinates, then operate with , and then change them back, i.e.: (73) • This equation can be rearranged: =0 • We can define the commutator (74) which is itself an operator 3 • For our inversion symmetric example system we have ,Θ 0.
    [Show full text]
  • Spin Density Wave Order, Topological Order, and Fermi Surface Reconstruction
    arXiv:1606.07813 Spin density wave order, topological order, and Fermi surface reconstruction Subir Sachdev,1, 2 Erez Berg,3 Shubhayu Chatterjee,1 and Yoni Schattner3 1Department of Physics, Harvard University, Cambridge MA 02138, USA 2Perimeter Institute for Theoretical Physics, Waterloo, Ontario, Canada N2L 2Y5 3Department of Condensed Matter Physics, The Weizmann Institute of Science, Rehovot, 76100, Israel (Dated: September 22, 2016) Abstract In the conventional theory of density wave ordering in metals, the onset of spin density wave (SDW) order co-incides with the reconstruction of the Fermi surfaces into small `pockets'. We present models which display this transition, while also displaying an alternative route between these phases via an intermediate phase with topological order, no broken symmetry, and pocket Fermi surfaces. The models involve coupling emergent gauge fields to a fractionalized SDW order, but retain the canonical electron operator in the underlying Hamiltonian. We establish an intimate connection between the suppression of certain defects in the SDW order, and the presence of Fermi surface sizes distinct from the Luttinger value in Fermi liquids. We discuss the relevance of such models to the physics of the hole-doped cuprates near optimal doping. arXiv:1606.07813v3 [cond-mat.str-el] 21 Sep 2016 1 I. INTRODUCTION A number of recent experiments [1{4] have highlighted a remarkable transformation in the electronic state of the hole-doped cuprates at a hole density around p = pc 0:19: many electronic ≈ properties change from those characteristic of a Fermi gas of charge +e carriers of density p for p < pc, to those of a Fermi gas of charge +e carriers of density 1 + p for p > pc.
    [Show full text]