DOCSLIB.ORG

Study Guide for the Final

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Study Guide for the Final Study Guide for the Final Math 330: History of Mathematics December 10, 2006. 1 Introduction What follows is a list of topics that might be on the Final. History is full of names of people, place names, and dates. Don’t worry: the only personal names, place names, or dates you need to memorize are given in this study guide. (Footnotes and parenthetical remarks in this study guide are given for information and clarification. You do not need to know them for the exam.) 2 Mathematicians 1. Thales from Miletus in Ionia, a Greek region on the coast of Asia Minor (in modern day Turkey). Said to have predicted an eclipse (of 585 BC) which actually occurred according to modern astronomers. Credited with the first use of proof in mathematics. Said to have brought geometry to Greece from Egypt. He is also credited with initiating the study of natural philosophy among the Greeks. He is given credit for several theorems including Thales’s theorem. 2. Pythagoras (6th century BC) from Samos, a Greek island close to Ionia. Lived later than Thales. He is said to have travelled to Egypt and Babylon, and learned from priests in the Egyptian and Babylonian religions. After coming back to the Greek world he founded a philosophical and religious society in Southern Italy (at Croton). He and his followers, called the Pythagoreans, were fascinated with mathematics, musical harmonies, and the concept of proportions and harmony in all aspects of life, and the universe or kosmos. The Pythagoreans included women as well as men. They discovered incommensurables, and at least some of the regular solids (including the dodecahedron). They were the first Greeks to make mathematics part of higher education. They were a very important influence on the later Greek mathematical tradition. In those days Mathematics, a term invented by Pythagoras, included arithmetic, geometry, music, and astronomy. At first, their knowledge was kept secret from outsiders. Pythagoras said that all is number, and discovered the simple mathematical ratios associated to harmonious notes in music. He is given credit for the first proof of the Pythagorean theorem (the theorem, but perhaps not the proof, was known to the Babylonians). 3. Hippocrates of Chios.1 Started out as a merchant, but during an extended stay in Athens due to a lawsuit, he decided to stay in Athens and do Geometry instead. Active in Athens 1Not to be confused with Hippocrates of Cos, the famous physician from about the same time who came up with the “Hippocratic oath”. 1 about the time of Socrates. Author of the first surviving fragment of Greek mathematics. In it, he showed that a certain lune is equal in area to a certain triangle. Thus he showed that some curved regions could be squared. He was apparently trying to square the circle, and his construction showed that some curved regions could be squared with straightedge and compass. Hippocrates was the first to write an Elements of geometry, now lost. He was also interested in duplicating the cube. He did not solve it completely, but he did reduce the problem to the problem of two mean proportionals: find x and y with a : x = x : y = y : 2a. The reduction of one problem to another is a common theme in mathematical research, and this example is the earliest known example of this phenomenon. (This idea was later used by Archytas, Menaechmus and Eratothenes to find a solution to the Delian problem.) 4. Eudoxus. The most famous mathematician associated with Plato’s Academy. Thought to have come up with some of the ideas incorporated into Euclid’s Elements, especially the theory of proportion and the method of exhaustion. (The theory of proportion is related to the modern idea of Dedekind cuts. The theory of exhaustion is based on a sophisticated use of proof by contradiction, and is an early example of a squeeze theorem. It is a precursor to integral calculus.) Eudoxus used the method of exhaustion to prove that the volume of a cone is one-third the base area times the height. Likewise, he proved that the volume of the pyramid is one-third the base area times the height. This last formula was known to the Egyptians, but Eudoxus seems to be the first to have proved it. Archimedes later applied the method of exhaustion to figure out the volume of a sphere, and to study other geometric volumes, areas, and centers of gravities. Eudoxus was also famous as an astronomer.2 5. Euclid. The first major mathematician who lived in Alexandria in Egypt, but he was likely educated in Athens. He lived after Alexander the Great (about 300 B.C.), and in his time the main center of mathematics shifted from Athens to Alexandria. The most famous mathemat- ics book of all times is Euclid’s Elements. King Ptolomy3, a successor to Alexander the Great who became king of Egypt, is said to have asked Euclid to show him a shorter way to learn geometry than the Elements. Euclid responded that there was no royal road to geometry. 6. Archimedes. Active in Syracuse in Sicily, before Sicily became part of the Roman Empire. (Syracuse was conquered by Rome in 212 BC on the day that Archimedes died.) He was amazingly talented in both pure mathematics and applied mathematics including engineering and early physics. You should know the following things he did: (i) Established the basics of hydrostatics and mechanics including the law of the lever and the law concerning the weight of a submerged object. (ii) Found areas, volumes, and centers of gravity associated with various surfaces and solids and gave proofs using the method of exhaustion. (iii) Approximated π 10 1 as 22/7 using inscribed and circumscribed 96-gons (he actually showed 3 71 < π < 3 7 ) and 2Eudoxus also worked on the Delian problem. In astronomy he developed an ingenious theory of planetary motion based on a complicated arrangement of 27 nested rotating spheres. He also wrote a book on geography. 3This Ptolomy is not the famous astronomer who lived later. 2 demonstrated that with enough skill and patience π could be approximated to arbitrarily high precision by using inscribed and circumscribed n-gons with n sufficiently large.4 (iv) Proved that the area of a circle was equal to the area of a certain triangle; describe this triangle.5 (v) Discovered and proved that the volume of a sphere was 2/3 that of the circumscribed cylinder. (vi) Discovered and proved that the surface area of a sphere was 2/3 that of the circumscribed cylinder. (vii) Showed that his spiral could be used to rectify and square the circle. (viii) Came up with a creative way to trisect an angle using a straightedge with two markings. (ix) Discovered the area of parabolic segments. Be able to answer the following: According to Archimedes’ hydrostatic principle, how much weight does a submerged object lose? What did he say when he discovered this law? What did this have to do with a crown allegedly of gold? How did Archimedes help in the defense of Syracuse? How did Archimedes die? What was inscribed on his tomb? Derive the modern formula for the area of the circle and the volume of the sphere using Archimedes result. 7. Apollonius (of Perga). Active in Alexandria (and Pergamum). A few decades younger than Archimedes. Famous for his work on conic sections. He was also famous for his work in astronomy. 8. Ptolomy. Lived in Alexandria which was then part of the Roman Empire. He was an astronomer, mathematician, and geographer. His most famous book is commonly called the Almagest (original name: Syntaxis Mathematica). This book gives a mathematical treatment of planetary motion, and the motion of the sun and the moon. His geocentric theory did not use simple circular orbits. What did it use? answer: epicyles. His complicated system represents the observations quite well. It needed to be complicated to be somewhat accurate since it was based on a flawed premise: the geocentric model of the solar system. What type of trigonometric function did he use? answer: the chord function. How is it related to sin θ? answer: Chord(θ) = 2 sin(θ/2). Draw a picture illustrating this. (Today we use a unit circle. Ptolomy used a circle of radius of 60 for convenience). He used base sixty and the idea of a circle having 360 degrees. These he inherited from the ancient Babylonians. 17 (He approximated π using an inscribed 360-gon: his value was 3 120 . He also cataloged the position of over a 1000 stars. Ptolomy also listed estimated latitudes and longtitudes of major known locations on the earth.) 9. Diophantus. Lived in Alexandria which was then part of the Roman Empire. First person to use algebraic symbolism instead of just words (syncopated algebra instead of rhetorical algebra). His book, the Arithmetica was quite sophisticated, certainly the most sophisticated algebra in the Greek speaking world. Solving equations for him requires methods quite a bit different than the standard methods taught today in algebra. This is mainly because he didn’t just want real number solutions, but wanted rational or integer solutions. His work later inspired Fermat to invent number theory. In fact, there is a modern branch of number theory called Diophantine equations. 10. Hypatia and the commentators Hypatia was more than just a mathematician. She was also a neo-Platonist philosopher and was known as a charismatic teacher. She wrote 4Archimedes and other ancient mathematicians did not use the letter π, instead they talked directly about the ratio of the circumference to the diameter or they referred to other related ratios.
Load more

Recommended publications
  • Squaring the Circle a Case Study in the History of Mathematics the Problem
    Squaring the Circle A Case Study in the History of Mathematics The Problem Using only a compass and straightedge, construct for any given circle, a square with the same area as the circle. The general problem of constructing a square with the same area as a given figure is known as the Quadrature of that figure. So, we seek a quadrature of the circle. The Answer It has been known since 1822 that the quadrature of a circle with straightedge and compass is impossible. Notes: First of all we are not saying that a square of equal area does not exist. If the circle has area A, then a square with side √A clearly has the same area. Secondly, we are not saying that a quadrature of a circle is impossible, since it is possible, but not under the restriction of using only a straightedge and compass. Precursors It has been written, in many places, that the quadrature problem appears in one of the earliest extant mathematical sources, the Rhind Papyrus (~ 1650 B.C.). This is not really an accurate statement. If one means by the “quadrature of the circle” simply a quadrature by any means, then one is just asking for the determination of the area of a circle. This problem does appear in the Rhind Papyrus, but I consider it as just a precursor to the construction problem we are examining. The Rhind Papyrus The papyrus was found in Thebes (Luxor) in the ruins of a small building near the Ramesseum.1 It was purchased in 1858 in Egypt by the Scottish Egyptologist A.
    [Show full text]
  • Reason in Motion
    Student Works 11-9-2018 Reason in Motion Luke Francis Embry-Riddle Aeronautical University, [email protected] Follow this and additional works at: https://commons.erau.edu/student-works Part of the Philosophy of Science Commons, and the The Sun and the Solar System Commons Scholarly Commons Citation Francis, L. (2018). Reason in Motion. , (). Retrieved from https://commons.erau.edu/student-works/82 This Article is brought to you for free and open access by Scholarly Commons. It has been accepted for inclusion in Student Works by an authorized administrator of Scholarly Commons. For more information, please contact [email protected]. Reason in Motion Luke Francis∗ Embry Riddle Aeronautical University Prescott, AZ 86301 (Dated: November 9, 2018) This essay will explain the historical models of the solar system, which was the known universe for most of human history. There is far more to each model than simply positioning different celestial bodies at the center of the system, and the stories of the astronomers who derived the controversial theories are not discussed often enough. The creation of these theories is part of a much broader revolution in scientific thought and marked the start of a series of observational discoveries that would change the the philosophy of science for centuries to come. I. STUDY PURPOSE Model. This was also influenced by metaphysical notions of human importance. In other words, man saw himself Although science and history are seen as two very sep- as the most important and the most divinely endowed arate fields of study, they depend greatly on each other.
    [Show full text]
  • GENERALIZED DEFORMATION-RATES in SECONDARY FLOWS of VISCOELASTIC FLUIDS BETWEEN ROTATING SPHERES Redacted for Privacy Kbstract Approved: M.N.L
    AN ABSTRACT OF THE THESIS OF RONALD NORMAN KNOSHAUG for the MASTER OF ARTS (Name) (Degree) in MATHEMATICS presented on October 10, 1968 (Major) (Date) Title: GENERALIZED DEFORMATION-RATES IN SECONDARY FLOWS OF VISCOELASTIC FLUIDS BETWEEN ROTATING SPHERES Redacted for Privacy kbstract approved: M.N.L. Narasimhan By various experiments, it has been found that the re- sponse of real materials to external forces is, in general, nonlinear in character. In classical continuum mechanics, the use of ordinary measures of strain have forced the constitutive equations to take complex forms and since the orders of these measures are not fixed, many unknown re- sponse coefficients have to be introduced into the consti- tutive equations. In general, there is no basis of choos- ing these coefficients. Seth attempted to resolve this difficulty by introducing generalized measures in continuum mechanics and Narasimhan and Sra extended these measures in such a way as to adequately explain some rheological behav- ior of materials. The constitutive equation of Narasimhan and Sra essentially contains two terms and four rheological constants and, unlike some previous theories, it does not contain any unknown functions of the invariants of kine- matic matrices while at the same time explains many visco- elastic phenomena. In the present investigation, a theorem has been proved establishing certain criteria for fixing the orders of generalized measures suitably so as to predict different types of viscoelastic phenomena, such as dilatancy. We have found during the course of this investigation that the constitutive equation of Narasimhan and Sra does not ade- quately explain such physical phenomena as pseudoplasticity.
    [Show full text]
  • The Method of Exhaustion
    The method of exhaustion The method of exhaustion is a technique that the classical Greek mathematicians used to prove results that would now be dealt with by means of limits. It amounts to an early form of integral calculus. Almost all of Book XII of Euclid’s Elements is concerned with this technique, among other things to the area of circles, the volumes of tetrahedra, and the areas of spheres. I will look at the areas of circles, but start with Archimedes instead of Euclid. 1. Archimedes’ formula for the area of a circle We say that the area of a circle of radius r is πr2, but as I have said the Greeks didn’t have available to them the concept of a real number other than fractions, so this is not the way they would say it. Instead, almost all statements about area in Euclid, for example, is to say that one area is equal to another. For example, Euclid says that the area of two parallelograms of equal height and base is the same, rather than say that area is equal to the product of base and height. The way Archimedes formulated his Proposition about the area of a circle is that it is equal to the area of a triangle whose height is equal to it radius and whose base is equal to its circumference: (1/2)(r · 2πr) = πr2. There is something subtle here—this is essentially the first reference in Greek mathematics to the length of a curve, as opposed to the length of a polygon.
    [Show full text]
  • Revolution of Charged Particles in a Central Field of Attraction with Emission of Radiation
    ISSN: 2639-0108 Research Article Advances in Theoretical & Computational Physics Revolution of Charged Particles in a Central Field of Attraction with Emission of Radiation Musa D Abdullahi *Corresponding author Musa D Abdullahi, Department of Electrical and Electronics Engineering, Department of Electrical and Electronics Engineering Kaduna Polytechnic, Kaduna, Nigeria. Submitted: 09 Jan 2020; Accepted: 20 Jan 2020; Published: 01 Feb 2020 Abstract A particle of mass nm, carrying the electronic charge -e, revolves in an orbit through angle ψ at distances nr from a center of force of attraction, with angular momenta nL perpendicular to the orbital plane, where n is an integer greater than 0, m the electronic mass and r1 is the radius of the first circular orbit. The equation of motion of the nth orbit of revolution is derived, revealing that an excited particle revolves in an unclosed elliptic orbit, with emission of radiation at the frequency of revolution, before settling down, after many cycles of ψ, in a stable circular orbit. In unipolar revolution, a radiating particle settles in a circular orbit of radius nr1 round a positively charged nucleus. In bipolar revolution, two radiating particles of the same mass nm and charges e and –e, settle in a circular stable orbit of radius ns1 round a common center of mass, where s1 is the radius of the first orbit. Discrete masses nm and angular momenta nL lead to quantization of the orbits outside Bohr’s quantum mechanics. The frequency of radiation in the bipolar revolution is found to be in conformity with the Balmer-Rydberg formula for the spectral lines of radiation from the atom hydrogen gas.
    [Show full text]
  • Medieval Mathematics
    Medieval Mathematics The medieval period in Europe, which spanned the centuries from about 400 to almost 1400, was largely an intellectually barren age, but there was significant scholarly activity elsewhere in the world. We would like to examine the contributions of five civilizations to mathematics during this time, four of which are China, India, Arabia, and the Byzantine Empire. Beginning about the year 800 and especially in the thirteenth and fourteenth centuries, the fifth, Western Europe, also made advances that helped to prepare the way for the mathematics of the future. Let us start with China, which began with the Shang dynasty in approximately 1,600 B. C. Archaeological evidence indicates that long before the medieval period, the Chinese had the idea of a positional decimal number system, including symbols for the digits one through nine. Eventually a dot may have been used to represent the absence of a value, but only during the twelfth century A. D. was the system completed by introducing a symbol for zero and treating it as a number. Other features of the Shang period included the use of decimal fractions, a hint of the binary number system, and the oldest known example of a magic square. The most significant book in ancient Chinese mathematical history is entitled The Nine Chapters on the Mathematical Art. It represents the contributions of numerous authors across several centuries and was originally compiled as a single work about 300 B. C. at the same time that Euclid was writing the Elements. However, in 213 B. C., a new emperor ordered the burning of all books written prior to his assumption of power eight years earlier.
    [Show full text]
  • Modeling Thin Fluid Film on a Rotary Bell
    University of Kentucky UKnowledge Theses and Dissertations--Mechanical Engineering Mechanical Engineering 2020 MODELING THIN FLUID FILM ON A ROTARY BELL Mark Doerre University of Kentucky, [email protected] Author ORCID Identifier: https://orcid.org/0000-0003-1105-3522 Digital Object Identifier: https://doi.org/10.13023/etd.2020.148 Right click to open a feedback form in a new tab to let us know how this document benefits ou.y Recommended Citation Doerre, Mark, "MODELING THIN FLUID FILM ON A ROTARY BELL" (2020). Theses and Dissertations-- Mechanical Engineering. 150. https://uknowledge.uky.edu/me_etds/150 This Doctoral Dissertation is brought to you for free and open access by the Mechanical Engineering at UKnowledge. It has been accepted for inclusion in Theses and Dissertations--Mechanical Engineering by an authorized administrator of UKnowledge. For more information, please contact [email protected]. STUDENT AGREEMENT: I represent that my thesis or dissertation and abstract are my original work. Proper attribution has been given to all outside sources. I understand that I am solely responsible for obtaining any needed copyright permissions. I have obtained needed written permission statement(s) from the owner(s) of each third-party copyrighted matter to be included in my work, allowing electronic distribution (if such use is not permitted by the fair use doctrine) which will be submitted to UKnowledge as Additional File. I hereby grant to The University of Kentucky and its agents the irrevocable, non-exclusive, and royalty-free license to archive and make accessible my work in whole or in part in all forms of media, now or hereafter known.
    [Show full text]
  • Mach New Water Old Buckets.Pdf
    1 “New Water in Old Buckets: Hypothetical and Counterfactual Reasoning in Mach’s Economy of Science”1 Lydia Patton, Virginia Tech 2019. Ernst Mach - Life, Work, and Influence / Ernst Mach - Leben, Werk und Wirkung, ed./hg. Friedrich Stadler. Vienna Circle Institute Yearbook. Dordrecht: Springer. Abstract Ernst Mach’s defense of relativist theories of motion in Die Mechanik in ihrer Entwickelung involves a well-known criticism of Newton’s theory appealing to absolute space, and of Newton’s “bucket” experiment in particular. Sympathetic readers including Norton (1995) and critics including Stein (1967, 1977) agree that there is a tension in Mach’s view: he allows for some constructed scientific concepts, but not others, and some kinds of reasoning about unobserved phenomena, but not others. Following Banks (2003), I argue that this tension can be interpreted as a constructive one, as springing from Mach’s basic approach to scientific reasoning. Mach’s reasoning about the “economy of science” allows for a principled distinction to be made, between natural and artificial hypothetical reasoning. Finally, Mach defends a division of labor between the sciences in a paper for The Monist of 1903, “Space and Geometry from the Point of View of Physical Inquiry”. That division supports counterfactual reasoning in Mach’s system, something that’s long been denied is possible for him. 1. Debating Mach’s Principle: Empiricism, Counterfactual Reasoning, and Economy 2. A Division of Labor within Mach’s Economy of Science 3. Mathematics and Mach’s Principle 2 1. Debating Mach’s Principle: Empiricism, Counterfactual Reasoning, and Economy The history of Mach’s Principle has been tied closely to the history of the theory of relativity, and thus, more broadly, to the history of relativistic theories of motion.
    [Show full text]
  • Conjectures and Refutations
    CONJECTURES AND REFUTATIONS -i- By the same Author The Open Society and Its Enemies Vol. I: The Spell of Plato Vol. II: The High Tide of Prophecy: Hegel, Marx, and the Aftermath The Poverty of Historicism The Logic of Scientific Discovery -ii- CONJECTURES AND REFUTATIONS The Growth of Scientific Knowledge by KARL R. POPPER BASIC BOOKS, Publishers NEW YORK LONDON -iii- © Karl R. Popper 1962 Manufactured in the United States of America -iv- TO F. A. VON HAYEK -v- Experience is the name every one gives to their mistakes. OSCAR WILDE -vi- PREFACE THE ESSAYS and lectures of which this book is composed are variations upon one very simple theme--the thesis that we can learn from our mistakes. They develop a theory of knowledge and of its growth. It is a theory of reason that assigns to rational arguments the modest and yet important role of criticizing our often mistaken attempts to solve our problems. And it is a theory of experience that assigns to our observations the equally modest and almost equally important role of tests which may help us in the discovery of our mistakes. Though it stresses our fallibility it does not resign itself to scepticism, for it also stresses the fact that knowledge can grow, and that science can progress--just because we can learn from our mistakes. The way in which knowledge progresses, and especially our scientific knowledge, is by unjustified (and unjustifiable) anticipations, by guesses, by tentative solutions to our problems, by conjectures. These conjectures are controlled by criticism; that is, by attempted refutations, which include severely critical tests.
    [Show full text]
  • 4 AN10 Abstracts
    4 AN10 Abstracts IC1 IC4 On Dispersive Equations and Their Importance in Kinematics and Numerical Algebraic Geometry Mathematics Kinematics underlies applications ranging from the design Dispersive equations, like the Schr¨odinger equation for ex- and control of mechanical devices, especially robots, to the ample, have been used to model several wave phenom- biomechanical modelling of human motion. The major- ena with the distinct property that if no boundary con- ity of kinematic problems can be formulated as systems ditions are imposed then in time the wave spreads out of polynomial equations to be solved and so fall within spatially. In the last fifteen years this field has seen an the domain of algebraic geometry. While symbolic meth- incredible amount of new and sophisticated results proved ods from computer algebra have a role to play, numerical with the aid of mathematics coming from different fields: methods such as polynomial continuation that make strong Fourier analysis, differential and symplectic geometry, an- use of algebraic-geometric properties offer advantages in alytic number theory, and now also probability and a bit of efficiency and parallelizability. Although these methods, dynamical systems. In this talk it is my intention to present collectively called Numerical Algebraic Geometry, are ap- few simple, but still representative examples in which one plicable wherever polynomials arise, e.g., chemistry, biol- can see how these different kinds of mathematics are used ogy, statistics, and economics, this talk will concentrate on in this context. applications in mechanical engineering. A brief review of the main algorithms of the field will indicate their broad Gigliola Staffilani applicability.
    [Show full text]
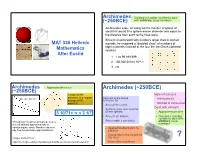
  • Archimedes (~250BCE) (~250BCE) Computed the Ideas of Calculus Perimeter of a Regular BD : CD = BA : AC
    Archimedes Created a number system to deal (~250BCE) with arbitrary large numbers Archimedes wrote an essay on the number of grains of sand that would fill a sphere whose diameter was equal to the distance from earth to the fixes stars. Since he had to work with numbers larger than in myriad MAT 336 Hellenic myriads, he imagined a “doubled class” of numbers of eight numerals (instead of the four the the Greek ciphered Mathematics system) After Euclid 1. 1 to 99,999,999 2. 100,000,000 to 1016-1 3. etc Archimedes Approximation of π Archimedes (~250BCE) (~250BCE) Computed the Ideas of calculus perimeter of a regular BD : CD = BA : AC. Derived and proved Infinitesimals polygon of 96 formulae for Method of exhaustion sides!!!!!! Area of the circle Dealt with infinity!!! Surface area and volume 3 10/71< π < 3 1/7 of the sphere Approximation of π Area of an ellipse. Created a number system to deal with Throughout this proof, Archimedes uses Area under a parabola arbitrary large several rational approximations to numbers various square roots. Nowhere does he Applied mathematics to say how he got those approximations. physics Explanation of principle of ? Images and text from: the lever https://itech.fgcu.edu/faculty/clindsey/mhf4404/archimedes/archimedes.html Innovative machines Archimedes (~250BCE) Archimedes Archimedes (~250BCE) (~250BCE) http://abel.math.harvard.edu/~knill//3dprinter/documents/paper.pdf Proposition 33: The surface of any sphere is equal to four times the circle in it. Proposition 34: Any sphere is equal to four times the cone
    [Show full text]
  • Squaring the Circle
    Squaring the Circle A Case Study in the History of Mathematics Part II π It is lost in the mists of pre-history who first realized that the ratio of the circumference of a circle to its diameter is a constant. All the ancient civilizations knew this fact. Today we call this ratio π and express this relationship by saying that for any circle, the circumference C and the diameter d satisfy: C = πd. The use of the symbol “π” for this ratio is of relatively recent origin; the Greeks did not use the symbol. “π was first used by the English mathematicians Oughtred (1647), Isaac Barrow (1664) and David Gregory (1697) to represent the circumference of a circle. The first use of “π” to represent the ratio of circumference to diameter was the English writer William Jones (1706). However, it did not come into common use until Euler adopted the symbol in 1737.1 Archimedes Euclid XII.2 says that the ratio of the area of any circle to the square of its diameter is also a constant, but does not determine the value of this constant. It was Archimedes (287 – 212 B.C.) who determined the constant in his remarkable treatise Measurement of a Circle. There are only three propositions in this short work (or at least, that is all of that work that has come down to us) and the second proposition is out of place – indicating that what we have is probably not the original version.2 We shall look at the first and third proposition.
    [Show full text]