A Quadrilateral That Has Two Pairs of Parallel Sides. • Rectangle
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Build a Tetrahedral Kite
Aeronautics Research Mission Directorate Build a Tetrahedral Kite Suggested Grades: 8-12 Activity Overview Time: 90-120 minutes In this activity, you will build a tetrahedral kite from Materials household supplies. • 24 straws (8 inches or less) - NOTE: The straws need to be Steps straight and the same length. If only flexible straws are available, 1. Cut a length of yarn/string 4 feet long. then cut off the flexible portion. • Two or three large spools of 2. Take six straws and place them on a flat surface. cotton string or yarn (approximately 100 feet total) 3. Use your piece of string to join three straws • Scissors together in a triangular shape. On the side where • Hot glue gun and hot glue sticks the two strings are extending from it, one end • Ruler or dowel rod for kite bridle should be approximately 20 inches long, and the • Four pieces of tissue paper (24 x other should be approximately 4 inches long. 18 inches or larger) See Figure 1. • All-purpose glue stick Figure 1 4. Tie these two ends of the string tightly together. Make sure there is no room for the triangle to wiggle. 5. The three straws should form a tight triangle. 6. Cut another 4-inch piece of string. 7. Take one end of the 4-inch string, and tie that end to a corner of the triangle that does not have the string ends extending from it. Figure 2. 8. Add two more straws onto the longest piece of string. 9. Next, take the string that holds the two additional straws and tie it to the end of one of the 4-inch strings to make another tight triangle. -

Square Rectangle Triangle Diamond (Rhombus) Oval Cylinder Octagon Pentagon Cone Cube Hexagon Pyramid Sphere Star Circle
SQUARE RECTANGLE TRIANGLE DIAMOND (RHOMBUS) OVAL CYLINDER OCTAGON PENTAGON CONE CUBE HEXAGON PYRAMID SPHERE STAR CIRCLE Powered by: www.mymathtables.com Page 1 what is Rectangle? • A rectangle is a four-sided flat shape where every angle is a right angle (90°). means "right angle" and show equal sides. what is Triangle? • A triangle is a polygon with three edges and three vertices. what is Octagon? • An octagon (eight angles) is an eight-sided polygon or eight-gon. what is Hexagon? • a hexagon is a six-sided polygon or six-gon. The total of the internal angles of any hexagon is 720°. what is Pentagon? • a plane figure with five straight sides and five angles. what is Square? • a plane figure with four equal straight sides and four right angles. • every angle is a right angle (90°) means "right ang le" show equal sides. what is Rhombus? • is a flat shape with four equal straight sides. A rhombus looks like a diamond. All sides have equal length. Opposite sides are parallel, and opposite angles are equal what is Oval? • Many distinct curves are commonly called ovals or are said to have an "oval shape". • Generally, to be called an oval, a plane curve should resemble the outline of an egg or an ellipse. Powered by: www.mymathtables.com Page 2 What is Cube? • Six equal square faces.tweleve edges and eight vertices • the angle between two adjacent faces is ninety. what is Sphere? • no faces,sides,vertices • All points are located at the same distance from the center. what is Cylinder? • two circular faces that are congruent and parallel • faces connected by a curved surface. -
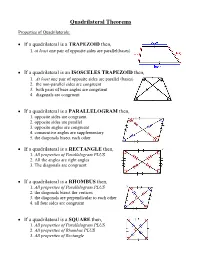
Quadrilateral Theorems
Quadrilateral Theorems Properties of Quadrilaterals: If a quadrilateral is a TRAPEZOID then, 1. at least one pair of opposite sides are parallel(bases) If a quadrilateral is an ISOSCELES TRAPEZOID then, 1. At least one pair of opposite sides are parallel (bases) 2. the non-parallel sides are congruent 3. both pairs of base angles are congruent 4. diagonals are congruent If a quadrilateral is a PARALLELOGRAM then, 1. opposite sides are congruent 2. opposite sides are parallel 3. opposite angles are congruent 4. consecutive angles are supplementary 5. the diagonals bisect each other If a quadrilateral is a RECTANGLE then, 1. All properties of Parallelogram PLUS 2. All the angles are right angles 3. The diagonals are congruent If a quadrilateral is a RHOMBUS then, 1. All properties of Parallelogram PLUS 2. the diagonals bisect the vertices 3. the diagonals are perpendicular to each other 4. all four sides are congruent If a quadrilateral is a SQUARE then, 1. All properties of Parallelogram PLUS 2. All properties of Rhombus PLUS 3. All properties of Rectangle Proving a Trapezoid: If a QUADRILATERAL has at least one pair of parallel sides, then it is a trapezoid. Proving an Isosceles Trapezoid: 1st prove it’s a TRAPEZOID If a TRAPEZOID has ____(insert choice from below) ______then it is an isosceles trapezoid. 1. congruent non-parallel sides 2. congruent diagonals 3. congruent base angles Proving a Parallelogram: If a quadrilateral has ____(insert choice from below) ______then it is a parallelogram. 1. both pairs of opposite sides parallel 2. both pairs of opposite sides ≅ 3. -

Cyclic Quadrilateral: Cyclic Quadrilateral Theorem and Properties of Cyclic Quadrilateral Theorem (For CBSE, ICSE, IAS, NET, NRA 2022)
9/22/2021 Cyclic Quadrilateral: Cyclic Quadrilateral Theorem and Properties of Cyclic Quadrilateral Theorem- FlexiPrep FlexiPrep Cyclic Quadrilateral: Cyclic Quadrilateral Theorem and Properties of Cyclic Quadrilateral Theorem (For CBSE, ICSE, IAS, NET, NRA 2022) Get unlimited access to the best preparation resource for competitive exams : get questions, notes, tests, video lectures and more- for all subjects of your exam. A quadrilateral is a 4-sided polygon bounded by 4 finite line segments. The word ‘quadrilateral’ is composed of two Latin words, Quadric meaning ‘four’ and latus meaning ‘side’ . It is a two-dimensional figure having four sides (or edges) and four vertices. A circle is the locus of all points in a plane which are equidistant from a fixed point. If all the four vertices of a quadrilateral ABCD lie on the circumference of the circle, then ABCD is a cyclic quadrilateral. In other words, if any four points on the circumference of a circle are joined, they form vertices of a cyclic quadrilateral. It can be visualized as a quadrilateral which is inscribed in a circle, i.e.. all four vertices of the quadrilateral lie on the circumference of the circle. What is a Cyclic Quadrilateral? In the figure given below, the quadrilateral ABCD is cyclic. ©FlexiPrep. Report ©violations @https://tips.fbi.gov/ 1 of 5 9/22/2021 Cyclic Quadrilateral: Cyclic Quadrilateral Theorem and Properties of Cyclic Quadrilateral Theorem- FlexiPrep Let us do an activity. Take a circle and choose any 4 points on the circumference of the circle. Join these points to form a quadrilateral. Now measure the angles formed at the vertices of the cyclic quadrilateral. -

THE GEOMETRY of PYRAMIDS One of the More Interesting Solid
THE GEOMETRY OF PYRAMIDS One of the more interesting solid structures which has fascinated individuals for thousands of years going all the way back to the ancient Egyptians is the pyramid. It is a structure in which one takes a closed curve in the x-y plane and connects straight lines between every point on this curve and a fixed point P above the centroid of the curve. Classical pyramids such as the structures at Giza have square bases and lateral sides close in form to equilateral triangles. When the closed curve becomes a circle one obtains a cone and this cone becomes a cylindrical rod when point P is moved to infinity. It is our purpose here to discuss the properties of all N sided pyramids including their volume and surface area using only elementary calculus and geometry. Our starting point will be the following sketch- The base represents a regular N sided polygon with side length ‘a’ . The angle between neighboring radial lines r (shown in red) connecting the polygon vertices with its centroid is θ=2π/N. From this it follows, by the law of cosines, that the length r=a/sqrt[2(1- cos(θ))] . The area of the iscosolis triangle of sides r-a-r is- a a 2 a 2 1 cos( ) A r 2 T 2 4 4 (1 cos( ) From this we have that the area of the N sided polygon and hence the pyramid base will be- 2 2 1 cos( ) Na A N base 2 4 1 cos( ) N 2 It readily follows from this result that a square base N=4 has area Abase=a and a hexagon 2 base N=6 yields Abase= 3sqrt(3)a /2. -

Lateral and Surface Area of Right Prisms 1 Jorge Is Trying to Wrap a Present That Is in a Box Shaped As a Right Prism
CHAPTER 11 You will need Lateral and Surface • a ruler A • a calculator Area of Right Prisms c GOAL Calculate lateral area and surface area of right prisms. Learn about the Math A prism is a polyhedron (solid whose faces are polygons) whose bases are congruent and parallel. When trying to identify a right prism, ask yourself if this solid could have right prism been created by placing many congruent sheets of paper on prism that has bases aligned one above the top of each other. If so, this is a right prism. Some examples other and has lateral of right prisms are shown below. faces that are rectangles Triangular prism Rectangular prism The surface area of a right prism can be calculated using the following formula: SA 5 2B 1 hP, where B is the area of the base, h is the height of the prism, and P is the perimeter of the base. The lateral area of a figure is the area of the non-base faces lateral area only. When a prism has its bases facing up and down, the area of the non-base faces of a figure lateral area is the area of the vertical faces. (For a rectangular prism, any pair of opposite faces can be bases.) The lateral area of a right prism can be calculated by multiplying the perimeter of the base by the height of the prism. This is summarized by the formula: LA 5 hP. Copyright © 2009 by Nelson Education Ltd. Reproduction permitted for classrooms 11A Lateral and Surface Area of Right Prisms 1 Jorge is trying to wrap a present that is in a box shaped as a right prism. -

Properties of Equidiagonal Quadrilaterals (2014)
Forum Geometricorum Volume 14 (2014) 129–144. FORUM GEOM ISSN 1534-1178 Properties of Equidiagonal Quadrilaterals Martin Josefsson Abstract. We prove eight necessary and sufficient conditions for a convex quadri- lateral to have congruent diagonals, and one dual connection between equidiag- onal and orthodiagonal quadrilaterals. Quadrilaterals with both congruent and perpendicular diagonals are also discussed, including a proposal for what they may be called and how to calculate their area in several ways. Finally we derive a cubic equation for calculating the lengths of the congruent diagonals. 1. Introduction One class of quadrilaterals that have received little interest in the geometrical literature are the equidiagonal quadrilaterals. They are defined to be quadrilat- erals with congruent diagonals. Three well known special cases of them are the isosceles trapezoid, the rectangle and the square, but there are other as well. Fur- thermore, there exists many equidiagonal quadrilaterals that besides congruent di- agonals have no special properties. Take any convex quadrilateral ABCD and move the vertex D along the line BD into a position D such that AC = BD. Then ABCD is an equidiagonal quadrilateral (see Figure 1). C D D A B Figure 1. An equidiagonal quadrilateral ABCD Before we begin to study equidiagonal quadrilaterals, let us define our notations. In a convex quadrilateral ABCD, the sides are labeled a = AB, b = BC, c = CD and d = DA, and the diagonals are p = AC and q = BD. We use θ for the angle between the diagonals. The line segments connecting the midpoints of opposite sides of a quadrilateral are called the bimedians and are denoted m and n, where m connects the midpoints of the sides a and c. -

Pentagonal Pyramid
Chapter 9 Surfaces and Solids Copyright © Cengage Learning. All rights reserved. Pyramids, Area, and 9.2 Volume Copyright © Cengage Learning. All rights reserved. Pyramids, Area, and Volume The solids (space figures) shown in Figure 9.14 below are pyramids. In Figure 9.14(a), point A is noncoplanar with square base BCDE. In Figure 9.14(b), F is noncoplanar with its base, GHJ. (a) (b) Figure 9.14 3 Pyramids, Area, and Volume In each space pyramid, the noncoplanar point is joined to each vertex as well as each point of the base. A solid pyramid results when the noncoplanar point is joined both to points on the polygon as well as to points in its interior. Point A is known as the vertex or apex of the square pyramid; likewise, point F is the vertex or apex of the triangular pyramid. The pyramid of Figure 9.14(b) has four triangular faces; for this reason, it is called a tetrahedron. 4 Pyramids, Area, and Volume The pyramid in Figure 9.15 is a pentagonal pyramid. It has vertex K, pentagon LMNPQ for its base, and lateral edges and Although K is called the vertex of the pyramid, there are actually six vertices: K, L, M, N, P, and Q. Figure 9.15 The sides of the base and are base edges. 5 Pyramids, Area, and Volume All lateral faces of a pyramid are triangles; KLM is one of the five lateral faces of the pentagonal pyramid. Including base LMNPQ, this pyramid has a total of six faces. The altitude of the pyramid, of length h, is the line segment from the vertex K perpendicular to the plane of the base. -

Performance Based Learning and Assessment Task Kite Project
Performance Based Learning and Assessment Task Kite Project I. ASSESSSMENT TASK OVERVIEW & PURPOSE: The students are instructed to: research the history, science, and design of kites; design a blueprint of their kite and find the measurements, scale factor, area, and perimeter of their blueprint; and construct and fly their kite. II. UNIT AUTHOR: Leslie Hindman, Washington-Lee High School, Arlington Public Schools III. COURSE: Geometry IV. CONTENT STRAND: Geometry, Measurement V. OBJECTIVES: Students will be able to • Design a scale model of a kite • Measure the dimensions and angles of the scale model • Determine the scale factor of the scale model • Compute the area and perimeter of the scale model • Construct and fly a kite VI. REFERENCE/RESOURCE MATERIALS: For Research: computer access For Scale Model Drawing: ruler, protractor, graph paper, calculator, Geometry SOL formula sheet For Kites: tissue paper, plastic table cloths, small wooden dowels, straws, yarn, fishing wire, markers, scissors, tape, glue VII. PRIMARY ASSESSMENT STRATEGIES: The task includes an assessment component that performs two functions: (1) for the student it will be a checklist and provide a self-assessment and (2) for the teacher it will be used as a rubric. The attached assessment list will assess the research section, scale model drawing, and kite construction. VIII. EVALUATION CRITERIA: Assessment List, corresponding rubric. IX. INSTRUCTIONAL TIME: 2 ninety minute class periods for research, scale model drawings, and kite construction. 1/2 ninety minute class period for flying kites. Kite Project Strand Geometry, Measurement Mathematical Objective(s) Students will be able to: • Design a scale model of a kite • Find the measures of the sides and angles of the scale model • Determine the scale factor of the scale model • Compute the area and perimeter of the scale model Related SOL • G.12 The student will make a model of a three-dimensional figure from a two- dimensional drawing and make a two-dimensional representation of a three- dimensional object. -

Module-03 / Lecture-01 SOLIDS Introduction- This Chapter Deals with the Orthographic Projections of Three – Dimensional Objects Called Solids
1 Module-03 / Lecture-01 SOLIDS Introduction- This chapter deals with the orthographic projections of three – dimensional objects called solids. However, only those solids are considered the shape of which can be defined geometrically and are regular in nature. To understand and remember various solids in this subject properly, those are classified & arranged in to two major groups- Polyhedron- A polyhedron is defined as a solid bounded by planes called faces, which meet in straight lines called edges. Regular Polyhedron- It is polyhedron, having all the faces equal and regular. Tetrahedron- It is a solid, having four equal equilateral triangular faces. Cube- It is a solid, having six equal square faces. Octahedron- It is a solid, having eight equal equilateral triangular faces. Dodecahedron- It is a solid, having twelve equal pentagonal faces. Icosahedrons- It is a solid, having twenty equal equilateral triangular faces. Prism- This is a polyhedron, having two equal and similar regular polygons called its ends or bases, parallel to each other and joined by other faces which are rectangles. The imaginary line joining the centre of the bases is called the axis. A right and regular prism has its axis perpendicular to the base. All the faces are equal rectangles. 1 2 Pyramid- This is a polyhedron, having a regular polygon as a base and a number of triangular faces meeting at a point called the vertex or apex. The imaginary line joining the apex with the centre of the base is known as the axis. A right and regular pyramid has its axis perpendicular to the base which is a regular plane. -

Apollonius of Pergaconics. Books One - Seven
APOLLONIUS OF PERGACONICS. BOOKS ONE - SEVEN INTRODUCTION A. Apollonius at Perga Apollonius was born at Perga (Περγα) on the Southern coast of Asia Mi- nor, near the modern Turkish city of Bursa. Little is known about his life before he arrived in Alexandria, where he studied. Certain information about Apollonius’ life in Asia Minor can be obtained from his preface to Book 2 of Conics. The name “Apollonius”(Apollonius) means “devoted to Apollo”, similarly to “Artemius” or “Demetrius” meaning “devoted to Artemis or Demeter”. In the mentioned preface Apollonius writes to Eudemus of Pergamum that he sends him one of the books of Conics via his son also named Apollonius. The coincidence shows that this name was traditional in the family, and in all prob- ability Apollonius’ ancestors were priests of Apollo. Asia Minor during many centuries was for Indo-European tribes a bridge to Europe from their pre-fatherland south of the Caspian Sea. The Indo-European nation living in Asia Minor in 2nd and the beginning of the 1st millennia B.C. was usually called Hittites. Hittites are mentioned in the Bible and in Egyptian papyri. A military leader serving under the Biblical king David was the Hittite Uriah. His wife Bath- sheba, after his death, became the wife of king David and the mother of king Solomon. Hittites had a cuneiform writing analogous to the Babylonian one and hi- eroglyphs analogous to Egyptian ones. The Czech historian Bedrich Hrozny (1879-1952) who has deciphered Hittite cuneiform writing had established that the Hittite language belonged to the Western group of Indo-European languages [Hro]. -

INTRODUCTION to QUADRILATERALS Square Rectangle Rhombus Parallelogram
INTRODUCTION TO QUADRILATERALS square rectangle rhombus parallelogram trapezoid kite Mathematicians define regular quadrilaterals according to their attributes. a) Quadrilaterals are two-dimensional closed figures that have four sides and four angles. b) The sum of their four angles is 360 degrees. c) When we trace diagonals from one opposite corner to another in a quadrilateral, these lines always intersect (pass it through) and in some cases they bisect (cut the other line in half). d) Regular quadrilaterals are named square, rectangle, parallelogram, rhombus, trapezoid, and kite. e) VERY IMPORTANT TO REMEMBER THIS! : Although these are the names of the quadrilaterals, these words are also the names of groups of quadrilaterals. Each group has its own characteristics or attributes that distinguish them from the others. For instance, the figure square belongs obviously to the group of squares, but also belongs to the groups of trapezoids, parallelograms, rectangles, rhombuses, and kites, because it shares similar attributes with them. However, the group of squares has only one figure: square. This is because no other quadrilateral shares the attributes of the squares, which are having four equal sides and four right angles. TRAPEZOIDS a) Trapezoids form the largest group of quadrilaterals. They include the figures of square, rectangle, parallelogram, rhombus, and of course, trapezoid. (the figure kite does not belong to the group of trapezoids) b) Trapezoids have only one attribute: they have at least one parallel line. Also, a. They may or may not have two or even four equal in length sides. b. They may or may not have opposite sides of the same length c.