Analyzing the Side Force on a Baseball Using Hawk-Eye Measurements
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Detroit Tigers Game Notes
DETROIT TIGERS GAME NOTES WORLD SERIES CHAMPIONS: 1935, 1945, 1968, 1984 Detroit Tigers Media Rela ons Department • Comerica Park • Phone (313) 471-2000 • Fax (313) 471-2138 • Detroit, MI 48201 www. gers.com • @ gers, @TigresdeDetroit, @DetroitTigersPR Detroit Tigers (9-14-4) at Philadelphia Phillies (10-15-1) Thursday, March 22, 2018 • Spectrum Field, Clearwater, FL • 1:05 p.m. ET LHP MaƩ hew Boyd (3-0, 4.50) vs. RHP Jake Arrieta (No Record) TV: MLB.TV • Radio: None RECENT RESULTS: The Tigers dropped a 3-2 decision to the Atlanta Braves on Wednesday night at Champion NUMERICAL ROSTER Stadium in Kissimmee. Mikie Mahtook belted a solo home run, his fi rst of the spring, while Niko Goodrum, 1 José Iglesias INF Leonys Mar n, Victor Reyes and Ronny Rodriguez each went 1x3 in the loss. Francisco Liriano started for 8 Mikie Mahtook OF Detroit, allowing two runs on four hits with fi ve walks and four strikeouts in 5.0 innings. Chad Bell and Drew 9 Nicholas Castellanos OF VerHagen each pitched a scoreless inning in relief with one strikeout. Warwick Saupold took the loss a er 12 Leonys Mar n OF giving up one run on one hit with one walk and one strikeout in 1.0 inning. The Tigers remain on the road 14 Alexi Amarista INF today as they travel to Clearwater to face the Philadelphia Phillies. 21 JaCoby Jones OF 22 Victor Reyes OF 24 Miguel Cabrera INF ROSTER MOVES: Prior to today's game, the Tigers announced the following roster moves: 27 Jordan Zimmermann RHP - Op oned LHP's Chad Bell and Blaine Hardy to Triple A Toledo 30 Alex Wilson RHP - Reassigned -

Dowd Scores in Overtime As Caps Edge Bruins in Game 1
ARAB TIMES, MONDAY, MAY 17, 2021 SPORTS 15 Bauer K’s 10, Muncy has 3 hits as Dodgers blank Marlins 7-0 Judge homers again, Yankees beat Orioles BALTIMORE, May 16, (AP): Aaron 4-3, 7-6 and 8-7 to win a back-and- Judge homered for the third time in forth game in which neither starting two games, Domingo Germán had pitcher made it past the third. The final another stellar outing at Camden Yards comeback by the Tigers came when and the New York Yankees beat the they scored twice off Kimbrel (0-2). Baltimore Orioles 8-2. Nomar Mazara tied it with an RBI Dowd scores in overtime as After hitting two home runs Friday, single that scored the automatic run- Judge provided New York a 5-0 lead ner, and JaCoby Jones ran for Mazara with a two-run shot in the second. Six and stole second. Then Castro — hit- of Judge’s 11 homers this season have less in five previous at-bats Saturday come against Baltimore. with three strikeouts — slapped a two- Germán (3-2) allowed one run and out single to left. The throw home by four hits with six strikeouts and two Kris Bryant was a bit off line and Caps edge Bruins in Game 1 walks over six innings. He has won all Jones was easily safe. four of his career starts in Baltimore. Matt Duffy homered and drove in Tyler Wade had three hits while bat- five runs for the Cubs. His RBI single ting ninth for New York, which off Michael Fulmer (3-2) gave the improved to 4-1 on its 10-game road Cubs the lead in the top of the 10th. -

09-29-2020 White Sox Wild Card Roster
2020 CHICAGO WHITE SOX ROSTER UPDATED: September 29, 2020 WHITE SOX COACHING STAFF, TRAINERS AND SUPPORT STAFF Manager: Rick Renteria (#17) | Coaches: Daryl Boston, First Base (#8); Nick Capra, Third Base (#12); Scott Coolbaugh, Asst. Hitting (#46) Don Cooper, Pitching (#21); Curt Hasler, Bullpen (#29); Joe McEwing, Bench (#82); Frank Menechino, Hitting (#22) Head Trainer: Brian Ball | Assistant Trainers: Brett Walker (Physical Therapist); James Kruk; Josh Fallin Strength/Conditioning: Allen Thomas (Director); Dale Torborg (Assistant) | Massage Therapist: Jessica Labunski Bullpen Catchers: Luis Sierra; Miguel González | Pre-Game Instructor and Replay: Mike Kashirsky Director of Team Travel: Ed Cassin | Video Coaching Coordinator: Bryan Johnson Clubhouse Managers: Rob Warren (Home); Jason Gilliam (Visiting); Joe McNamara Jr. (Umpires) WHITE SOX ACTIVE ROSTER (28) NUMERICAL ROSTER (28) No. Pitchers (13) B T HT WT Born Birthplace Residence No. Player Pos. 39 Aaron Bummer L L 6-3 215 9/21/93 Valencia, Calif. Omaha, Neb. 1 Nick Madrigal ...............................2B 84 Dylan Cease R R 6-2 200 12/28/95 Milton, Ga. Ball Ground, Ga. 5 Yolmer Sánchez .........................INF 48 Alex Colomé ("co-low-MAY") R R 6-1 225 12/31/88 Santo Domingo, D.R. San Pedro de Macorís, D.R. 7 Tim Anderson ..............................SS 50 Jimmy Cordero R R 6-4 235 10/19/91 San Cristóbal, D.R. Reading, Pa. 10 Yoán Moncada ............................INF 45 Garrett Crochet ("CROW-shay") L L 6-6 220 6/21/99 Ocean Springs, Miss. Ocean Springs, Miss. 15 Adam Engel .................................OF 51 Dane Dunning R R 6-4 225 12/20/94 Orange Park, Fla. -
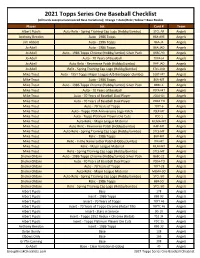
2021 Topps Series One Checklist Baseball
2021 Topps Series One Baseball Checklist (All Cards except unannounced Base Variations); Orange = Auto/Relic; Yellow = Base Rookie Player Set Card # Team Albert Pujols Auto Relic - Spring Training Cap Logo (Hobby/Jumbo) STCL-AP Angels Anthony Rendon Auto - 1986 Topps 86A-ARE Angels Jim Abbott Auto - 1986 Topps 86A-JA Angels Jo Adell Auto - 1986 Topps 86A-JAD Angels Jo Adell Auto - 1986 Topps Chrome (Hobby/Jumbo) Silver Pack 86BC-90 Angels Jo Adell Auto - 70 Years of Baseball 70YA-JA Angels Jo Adell Auto Relic - Reverence Patch (Hobby/Jumbo) RAP-JAD Angels Jo Adell Relic - Spring Training Cap Logo (Hobby/Jumbo) STCL-JAD Angels Mike Trout Auto - 1951 Topps Major League A/S Boxtopper (Jumbo) 51BT-MT Angels Mike Trout Auto - 1986 Topps 86A-MT Angels Mike Trout Auto - 1986 Topps Chrome (Hobby/Jumbo) Silver Pack 86BC-1 Angels Mike Trout Auto - 70 Years of Baseball 70YA-MT Angels Mike Trout Auto - 70 Years of Baseball Dual Player 70DA-GT Angels Mike Trout Auto - 70 Years of Baseball Dual Player 70DA-TO Angels Mike Trout Auto - 70 Years of Topps 70YT-6 Angels Mike Trout Auto - Topps 70th Anniversary Logo Patch 70LP-MT Angels Mike Trout Auto - Topps Platinum Players Die Cuts PDC-1 Angels Mike Trout Auto Relic - Major League Material MLMA-MT Angels Mike Trout Auto Relic - Reverence Patch (Hobby/Jumbo) RAP-MT Angels Mike Trout Auto Relic - Spring Training Cap Logo (Hobby/Jumbo) STCL-MT Angels Mike Trout Relic - 1986 Topps 86R-MT Angels Mike Trout Relic - In the Name Letter Patch (Hobby/Jumbo) ITN-MT Angels Mike Trout Relic - Major League Material -

Rubberducks Game Notes 051418
2018 Akron RubberDucks Game Notes Trenton Thunder (22-13) vs. Akron RubberDucks (21-15) New York Yankees Cleveland Indians Game 37 • Monday, May 14, 2018 • 7:00 p.m. ARM & HAMMER Park • Trenton, NJ Radio: WARF 1350 AM • WARF iHeart Channel • TuneIn App • Television: MiLB.TV Today’s Starting Pitchers: Mon. 5/14, 7:00 p.m. at Trenton: Akron: LHP Matt Whitehouse (1-1, 2.57) Trenton: RHP Dillon Tate (1-2, 4.60) Upcoming Games and Pitching Probables (subject to change): Tue. 5/15, 7:00 p.m. at Trenton: Akron: RHP Dominic DeMasi (3-1, 3.48) Trenton: RHP Jonathan Loaisiga (1-0, 1.80) Wed. 5/16, 10:30 a.m. at Trenton: Akron: LHP Sean Brady (1-3, 4.28) Trenton: RHP Erik Swanson (5-0, 0.52) Thu. 5/17, 7:05 p.m. at Hartford: Akron: RHP Shao-Ching Chiang (3-0, 2.08) Hartford: TBA Fri. 5/18, 7:05 p.m. at Hartford: Akron: RHP Jake Paulson (2-1, 2.79) Hartford: TBA RubberDucks News and Notes: Last Time Out Erie’s Spencer Turnbull combined with three relievers on a six-hit shutout, and Jake Robson cracked a key RBI single, as the SeaWolves blanked the Akron RubberDucks, 2-0, Sunday afternoon at Canal Park in Akron, Ohio. Where We Stand At 21-15, the RubberDucks are in 1st place in the EL West, 1.5 games ahead of 2nd-place Altoona and Richmond. The RubberDucks… -were shutout for the fourth time this season. -lost three out of four to Erie and have dropped four of the last five, overall. -
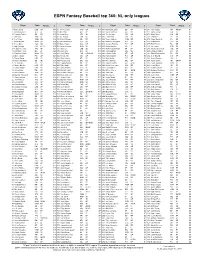
NL-Only Leagues
ESPN Fantasy Baseball top 360: NL-only leagues Player Team All pos. $ Player Team All pos. $ Player Team All pos. $ Player Team All pos. $ 1. Mookie Betts LAD OF $44 91. Joc Pederson CHC OF $14 181. MacKenzie Gore SD SP $7 271. John Curtiss MIA RP/SP $1 2. Ronald Acuna Jr. ATL OF $39 92. Will Smith ATL RP $14 182. Stefan Crichton ARI RP $6 272. Josh Fuentes COL 1B $1 3. Fernando Tatis Jr. SD SS $37 93. Austin Riley ATL 3B $14 183. Tim Locastro ARI OF $6 273. Wade Miley CIN SP $1 4. Juan Soto WSH OF $36 94. A.J. Pollock LAD OF $14 184. Lucas Sims CIN RP $6 274. Chad Kuhl PIT SP $1 5. Trea Turner WSH SS $32 95. Devin Williams MIL RP $13 185. Tanner Rainey WSH RP $6 275. Anibal Sanchez FA SP $1 6. Jacob deGrom NYM SP $30 96. German Marquez COL SP $13 186. Madison Bumgarner ARI SP $6 276. Rowan Wick CHC RP $1 7. Trevor Story COL SS $30 97. Raimel Tapia COL OF $13 187. Gregory Polanco PIT OF $6 277. Rick Porcello FA SP $0 8. Cody Bellinger LAD OF/1B $30 98. Carlos Carrasco NYM SP $13 188. Omar Narvaez MIL C $6 278. Jon Lester WSH SP $0 9. Freddie Freeman ATL 1B $29 99. Gavin Lux LAD 2B $13 189. Anthony DeSclafani SF SP $6 279. Antonio Senzatela COL SP $0 10. Christian Yelich MIL OF $29 100. Zach Eflin PHI SP $13 190. Josh Lindblom MIL SP $6 280. -

TENTATIVE GATOR LINEUP Eastern Michigan (0-0, MAC) Tuesday
WEEK 2 | GATORS & EAGLES BATTLE IN MIDWEEK SERIES | TUESDAY-WEDNESDAY, FEBRUARY 23-24 | GAINESVILLE, FL (TUESDAY) & LAKELAND, FL (WEDNESDAY) John Hines, Associate Communications Director University Athletic Association - Communications Department P.O. Box 14485 | Gainesville, FL 32604 Cell: 352-317-7386 | Office: 352-375-4683 | E-Mail: [email protected] www.FloridaGators.com | Twitter: @GatorsBB | Instagram: gatorsbb 9 COLLEGE WORLD SERIES APPEARANCES | 31 NCAA REGIONAL APPEARANCES | 13 SEC CHAMPIONSHIPS | 22 SEC EASTERN DIVISION TITLES | 7 SEC TOURNAMENT CHAMPIONSHIPS 4Radio: Jeff Cardozo & Steve Russell will call the action on the Gator IMG Sports Network 2016 GATOR BASEBALL SCHEDULE & RESULTS 4Television: None 4Internet: Live stats & audio through FloridaGators.com FEBRUARY 4Series: Florida leads 5-1; all meetings in Gainesville; More info on page 2 19 FGCU (SEC+) 7 p.m. W, 4-2 4Rankings: UF is 1st in Baseball America, Collegiate Baseball, D1Baseball, NCBWA, Perfect Game & USA 20 FGCU (SEC+) 4 p.m. W, 8-4 21 FGCU (SEC+) 1 p.m. W, 12-3 Today 23 EASTERN MICHIGAN 7 p.m. 4Head Coaches: Kevin O’Sullivan, 9th year at Florida and overall, 347-173 (.667); Mark Van Ameyde, 2nd 24 vs. E. Michigan (Lakeland) 7 p.m. year at Eastern Michigan and overall, 23-36 (.390) 26 @Miami (FL) (ESPN3) 7 p.m. 27 @Miami (FL) (ESPN3) 7 p.m. Eastern Michigan Tuesday: Kevin Shul, Jr. (R) (0-0, 0.00) Dane Dunning, Jr., (R) (0-0, 9.00) 28 @Miami (FL) (ESPN3) 1 p.m. EAGLES Wednesday: TBA Scott Moss, So., (L) (0-0, 0.00) MARCH (0-0, MAC) 1 @UCF 6:30 p.m. -

Baltimore Orioles Game Notes
BALTIMORE ORIOLES GAME NOTES ORIOLE PARK AT CAMDEN YARDS • 333 WEST CAMDEN STREET • BALTIMORE, MD 21201 MONDAY, AUGUST 20, 2018 • GAME #125 • ROAD GAME #64 BALTIMORE ORIOLES (37-87) at TORONTO BLUE JAYS (55-69) RHP Andrew Cashner (4-10, 4.71) vs. RHP Marco Estrada (6-9, 4.87) CEDRIC THE ENTERTAINER: OF Cedric Mullins went 2-for-3 on Sunday at Cleveland and hit his first career home run Saturday...Since I’VE GOT YOUR BACK making his Major League debut on August 10, he is batting .387 (12-for-31) and six of his 12 hits are extra-base hits...Mullins has five Lowest inherited runners scored percentage in doubles through nine career games...He is the first Orioles batter with at least five doubles through nine career games since current Orioles the American League (by team): assistant hitting coach Howie Clark notched five doubles in 2002...Since making his debut on August 10, Mullins’ .387 batting average 1. Los Angeles-AL 20.6% (43-of-209) leads AL rookies and ranks second in the majors among rookies behind Atlanta’s Ronald Acuña, Jr. (.450)...His five doubles since August 2. Houston 24.6% (32-of-130) 10 are tied for second-most in the majors among rookies. 3. Cleveland 27.0% (48-for-178) 4. Boston 28.2% (37-of-131) BREAKING NEWS: The Orioles rank among league leaders in several major offensive categories since the All-Star break, including 5. BALTIMORE 29.1% (67-of-230) ranking third in the majors in batting average at .276 (257-for-931)...They have recorded 257 hits in 26 games since the All-Star break, 6. -

List of Players in Apba's 2018 Base Baseball Card
Sheet1 LIST OF PLAYERS IN APBA'S 2018 BASE BASEBALL CARD SET ARIZONA ATLANTA CHICAGO CUBS CINCINNATI David Peralta Ronald Acuna Ben Zobrist Scott Schebler Eduardo Escobar Ozzie Albies Javier Baez Jose Peraza Jarrod Dyson Freddie Freeman Kris Bryant Joey Votto Paul Goldschmidt Nick Markakis Anthony Rizzo Scooter Gennett A.J. Pollock Kurt Suzuki Willson Contreras Eugenio Suarez Jake Lamb Tyler Flowers Kyle Schwarber Jesse Winker Steven Souza Ender Inciarte Ian Happ Phillip Ervin Jon Jay Johan Camargo Addison Russell Tucker Barnhart Chris Owings Charlie Culberson Daniel Murphy Billy Hamilton Ketel Marte Dansby Swanson Albert Almora Curt Casali Nick Ahmed Rene Rivera Jason Heyward Alex Blandino Alex Avila Lucas Duda Victor Caratini Brandon Dixon John Ryan Murphy Ryan Flaherty David Bote Dilson Herrera Jeff Mathis Adam Duvall Tommy La Stella Mason Williams Daniel Descalso Preston Tucker Kyle Hendricks Luis Castillo Zack Greinke Michael Foltynewicz Cole Hamels Matt Harvey Patrick Corbin Kevin Gausman Jon Lester Sal Romano Zack Godley Julio Teheran Jose Quintana Tyler Mahle Robbie Ray Sean Newcomb Tyler Chatwood Anthony DeSclafani Clay Buchholz Anibal Sanchez Mike Montgomery Homer Bailey Matt Koch Brandon McCarthy Jaime Garcia Jared Hughes Brad Ziegler Daniel Winkler Steve Cishek Raisel Iglesias Andrew Chafin Brad Brach Justin Wilson Amir Garrett Archie Bradley A.J. Minter Brandon Kintzler Wandy Peralta Yoshihisa Hirano Sam Freeman Jesse Chavez David Hernandez Jake Diekman Jesse Biddle Pedro Strop Michael Lorenzen Brad Boxberger Shane Carle Jorge de la Rosa Austin Brice T.J. McFarland Jonny Venters Carl Edwards Jackson Stephens Fernando Salas Arodys Vizcaino Brian Duensing Matt Wisler Matt Andriese Peter Moylan Brandon Morrow Cody Reed Page 1 Sheet1 COLORADO LOS ANGELES MIAMI MILWAUKEE Charlie Blackmon Chris Taylor Derek Dietrich Lorenzo Cain D.J. -

2017 Minor League Report 4-30-2017.Indd
DETROIT TIGERS MINOR LEAGUE REPORT (Through Games of Saturday, April 29) TOLEDO MUD HENS (TRIPLE A) ERIE SEAWOLVES (DOUBLE A) Record/Standings: 11-10, 1st, 2.5 GA in Interna onal League West Division Record/Standings: 10-10, T-3rd, 1.5 GB in Eastern League Western Division Yesterday’s Score: PPD., Rain vs. Lehigh Valley Yesterday’s Score: L, 7-4 @ Trenton Streak/Last 10: W1/3-7 Streak/Last 10: L1/3-7 Next Game: 4/30 vs. Lehigh Valley, 2:05 p.m. Next Game: 4/30 @ Trenton, 1:00 p.m. Yesterday’s Recap: Triple A Toledo lost the fi rst game of the doubleheader to Lehigh Yesterday’s Recap: Double A Erie lost 7-4 to Trenton on Saturday night, Valley, 6-1, on Saturday a ernon, but won the second, 2-1 in extra innings. In the fi rst dropping them to third in the Western Division. Anthony Vasquez started and game, Dus n Molleken pitched 2.0 innnings in relief, allowing unearned run, on two hits pitched 5.0 innings, allowing four runs (three earned), on six hits with four with four strikeouts. Off ensively, Brendan Ryan went 1x2, and drove in the only Mud Hens strikeouts. Adam Ravenelle and Kurt Spomer combined to pitch two scoreless run of the game. In the second game, Edward Mujica picked up his fi rst win of the season, innings in relief. Off ensively, Mike Gerber went 3x5, with a double and two runs pitching 1.0 scoreless inning in relief, and striking out two. Argenis Diaz went 2x4, and scored. -

Atlanta Braves Schedule
2020 60GAME ATLANTA BRAVES SCHEDULE JULYJULY SUN MON TUE WED THU FRI SAT 1 2 3 4 HOME AWAY 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 4:10 25 4:10 26 7:08 27 6:40 28 6:40 29 7:10 30 7:10 31 7:10 AUGUSTAUGUST SUN MON TUE WED THU FRI SAT 1 7:10 2 1:10 3 7:10 4 7:10 5 7:10 6 7:10 7 7:05 8 6:05 9 1:05 10 6:05 11 7:05 12 7:05 13 14 7:10 15 6:10 16 1:10 17 7:10 18 7:10 19 7:10 20 21 7:10 22 7:10 / / / / 23 1:10 24 25 7:10 26 7:10 27 28 7:05 29 1:15 30 7:08 31 7:30 SEPTEMBERSEPTEMBER SUN MON TUE WED THU FRI SAT 1 7:30 2 7:30 3 4 7:10 5 7:10 6 1:10 7 1:10 8 7:10 9 7:10 10 6:05 11 6:05 12 6:05 13 12:35 14 7:35 15 7:35 16 7:35 17 18 7:10 19 7:07 BB&T and SunTrust are now Truist 20 1:10 21 7:10 22 7:10 23 7:10 24 7:10 25 7:10 26 7:10 Together for better 27 3:10 28 29 30 WATCH ON: LISTEN ON: truist.com Truist Bank, Member FDIC. -

Take Me out to the Old Yakyu
Take Me Out to the Old Yakyu You might never believe it when you look at American store shelves crowded with Japanese transistor radios, binoculars, and cameras, but ships also sail the other way, carrying American products and ideas to Japan. And at least one American game - baseball - has had amazing success there. Some ten million Japanese pay their way into the ball parks of the two six-team leagues every season, and uncounted other millions sit transfixed in front of TV sets, sloshing down their maki-zuski (raw-fish covered with rice and wrapped in seaweed) with good Japanese lager beer. The country is less than two-thirds the size of Texas, yet the Japanese boast forty stadiums, complete with lights for night ball, capable of staging major league ball games. Vacant lots of Japan are all one size - small - but kids play baseball on all of them. Profits are not a problem for Japanese baseball teams. Except for the Tokyo Giants, none of them makes money. Teams are all owned by corporations that use them for public relations, and the clubs are usually named not for cities but for the companies that control them. The Nankai Hawks and the Hankyu Braves both play in Osaka and are owned by railroads. Organized baseball has been part of the Japanese sports scene since the early 1930's. An American witnessing a Japanese game would certainly recognize it as baseball, but he would also realize that the game has acquired a distinct Japanese flavor, starting with the name of the game, which they call yakyu.