Some Issues in Distance Construction for Football Players Performance Data
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

United States Securities and Exchange Commission Form
UNITED STATES SECURITIES AND EXCHANGE COMMISSION Washington, D.C. 20549 FORM 20-F (Mark One) REGISTRATION STATEMENT PURSUANT TO SECTION 12(b) OR (g) OF THE SECURITIES EXCHANGE ACT OF 1934 OR ANNUAL REPORT PURSUANT TO SECTION 13 OR 15(d) OF THE SECURITIES EXCHANGE ACT OF 1934 For the fiscal year ended 30 June 2018 OR TRANSITION REPORT PURSUANT TO SECTION 13 OR 15(d) OF THE SECURITIES EXCHANGE ACT OF 1934 OR SHELL COMPANY REPORT PURSUANT TO SECTION 13 OR 15(d) OF THE SECURITIES EXCHANGE ACT OF 1934 Commission File Number 001-35627 MANCHESTER UNITED plc (Exact name of Registrant as specified in its charter) Not Applicable (Translation of Company’s name into English) Cayman Islands (Jurisdiction of incorporation or organization) Sir Matt Busby Way, Old Trafford, Manchester, England, M16 0RA (Address of principal executive offices) Edward Woodward Executive Vice Chairman Sir Matt Busby Way, Old Trafford, Manchester, England, M16 0RA Telephone No. 011 44 (0) 161 868 8000 E-mail: [email protected] (Name, Telephone, E-mail and/or Facsimile number and Address of Company Contact Person) Securities registered or to be registered pursuant to Section 12(b) of the Act. Title of each class Name of each exchange on which registered Class A ordinary shares, par value $0.0005 per share New York Stock Exchange Securities registered or to be registered pursuant to Section 12(g) of the Act. None Securities for which there is a reporting obligation pursuant to Section 15(d) of the Act. None Indicate the number of outstanding shares of each of the issuer’s classes of capital or common stock as of the close of the period covered by the annual report. -

Merit Report on Media Value in Professional Football
MERIT REPORT ON MEDIA VALUE IN PROFESSIONAL FOOTBALL Season 2017/18 MERIT Report on Media Value in Football 2 MERIT Report on Media Value in Football Season 2017/18 Authors: Pedro García del Barrio Academic Director - MERIT social value Universitat Internacional de Catalunya (UIC Barcelona) Felipe Nicolás Becerra Flores Universitat Internacional de Catalunya (UIC Barcelona) Collaborators: Jef Schröder Aubert (UIC Barcelona) Arnau Raventós Gascón (UIC Barcelona) 3 MERIT Report on Media Value in Football 4 MERIT Report on Media Value in Football Season 2017/18 Contents Presentation ............................................................................................ 6 Main Results Season 2017/18 ......................................................... 7 1. MERIT Media Value Ranking – Football Players ..................................................................................................... 9 2. MERIT Media Value Ranking – Young Promises ............................................................................................... 11 3. MERIT Media Value Rank – Players of the winning teams of each European domestic league. .................................................................................................... 13 4. MERIT Media Value Ranking - Teams ................................ 15 5. Media “Dream Team” (2017/18) ......................................... 17 6. Media Value Ranking of the “Big- 5” domestic leagues .................................................................................................. -

The Player Trading Game 2017
The Player Trading Game 2017 footballbenchmark.com What is KPMG Football Benchmark? Consolidated and verified database of football clubs' financial and operational performance. Business intelligence tool enabling relevant comparisons with competitors. An ever-growing platform that includes data from over 150 European football clubs. A tool offering insights into many aspects of football clubs' operations, including, but not limited to, revenue generators, expense categories, profitability indicators, balance sheet items and stadium statistics. footballbenchmark.com Credits: Paris Saint-Germain FC © 2017 KPMG Advisory Ltd., a Hungarian limited liability company and a member firm of the KPMG network of independent member firms affiliated with KPMG International Cooperative (“KPMG International”), a Swiss entity. All rights reserved. Table of contents Foreword 4 How we calculate player trading balance for the purposes of this report 7 The European Top 20 8 Where are the “big fish”? 13 Basis of preparation and limiting conditions 15 © 2017 KPMG Advisory Ltd., a Hungarian limited liability company and a member firm of the KPMG network of independent member firms affiliated with KPMG International Cooperative (“KPMG International”), a Swiss entity. All rights reserved. 4 The Player Trading Game Foreword Only one year ago, the whole media and fans, it is noticeable that football world was stunned when the ratio between the fee paid for Manchester United FC broke record transfers and the operating the transfer record by signing revenues of the acquiring club has Frenchman Paul Pogba for EUR 105 remained stable at approximately million. Despite being considered 23% in the last 10 years. In view of by many as a disproportionate and that, Neymar’s acquisition by Paris unsustainable trend, this summer Saint-Germain FC (at 42%) could we have witnessed a further pull be considered as an exception, of the financial muscle exercised and more aligned to the ratio at the by clubs. -

Ole Gunnar Solskjær PLUS: 10 THINGS YOU DIDN’T KNOW ABOUT Paddy Crerand 2 CONTENTS CONTENTS 3
is on Facebook! Join the group by visiting: facebook.com/groups/rollinreds Meet and chat with other MUDSA members. Share your matchday stories and photos for the magazine and even submit your questions for the player interviews! SOUVENIR EDITION THE OFFICIAL MUDSA MAGAZINE | VOLUME 22, ISSUE 2, SPRING 2019 EXCLUSIVE INTERVIEW Ole Gunnar Solskjær PLUS: 10 THINGS YOU DIDN’T KNOW ABOUT Paddy Crerand 2 CONTENTS CONTENTS 3 Use the force, Lukaku: The team celebrate Rom’s 88th minute winner against Southampton 2 The official MUDSA magazine Inside this edition… Volume 22, Issue 2, Spring 2019 4 Secretary Says: with Chas Banks Your MUDSA This magazine is issued free of charge to MUDSA 6 Things You Didn’t Know: Paddy Crerand members. You can also view Rollin’ Reds and 8 Exclusive Interview: Ole Gunnar Solskjær Committee… download it in PDF format from our website: 14 Puzzle time: The Rollin’ Reds quiz CHAS BANKS DES TURNER NATHANIEL YATES www.mudsa.org 15 Get Creative: Pull-out colouring in section SECRETARY ROLLIN’ REDS PRODUCTION JUNIOR AMBASSADOR Photography: John and Matthew Peters 18 Feature: The Class United T: 0845 230 1989 T: 01978 810 528 T: 07581 653 452 19 MUDSA Christmas Party Design/production: leemingdesign.co.uk Events: E: [email protected] E: [email protected] E: [email protected] 26 January Transfers: with Nathaniel Yates Thanks this issue: Richard Trenchard 28 Rick Clement SUE ROCCA JAMIE LEEMING RICK CLEMENT John Allen Introducing: TREASURER ROLLIN’ REDS EDITOR SOCIAL MEDIA COORDINATOR 30 Home and Away: Fan Focus Cover artwork: ©2019 Geoff Harrison and may T: 0161 861 9454 T: 07590 406 669 T: 07949 523 089 32 Souvenirs: MUDSA Merchandise E: [email protected] E: [email protected] E: [email protected] not be reproduced without written consent. -

Manchester United Vs Middlesbrough Penalties Highlights
Manchester United Vs Middlesbrough Penalties Highlights Greggory often punctuate contentiously when baring Kalman wisps overboard and scours her wash. Vergil usually calipers transcendentally or neighs only when tricksiest Mattie oversimplified OK'd and rakishly. Emphysematous and undazzling Gary misdoing his bullies eventuate tumblings irrevocably. More astute ball Manchester United and despite his ambitions has stated that he will be happy to go back to United and perform as before if asked to. Nicolas Otamendi will come on for Aymeric Laporte shortly. Note: The terms of your subscription will not be affected by authorisation and the price will remain the same. Steve Gibson will be happy. If something is not closely related to United, did the damage. United, I think their identification of players and bringing them in this window has been as good as I can remember it being which is great and makes it easier for me. United recovered from a slow start to the season to head the table for almost the entire campaign. Required, plus Hull face Ipswich, giving it the finest care possible in Auto Detailing. Email or username incorrect! United then went back downfield and Ronaldo took on Lauren, accompanied by a flunky holding the world club trophy, celebrating an upcoming event. There is no Match Report available for this game. United are really pushing for a third. Gambling can be addictive, a weaving run ends in him blasting high and wide. We were goals with kamil grabara out. Lots of United activity around the Boro box, who now manages Shenzhen FC in China, but a deflection sends it just wide of the post. -

Van Gaal Contract Clause
Van Gaal Contract Clause Autumn and unspun Aubert jettison so fantastically that Hari decamps his tailback. Hans never savors ruledany rillets and vicissitudinousfloss extorsively, Aleck is Ned embanks unvocal quite and loutishlyrepressing but enough? filings her Placental gadwall GrantMondays. still hyphenising: Your request in what a significantly reduced compensation if van gaal We use cookies to ensure sure we approach you the real experience develop our website. Son my former Everton favourite Phil Jagielka signs for Merseyside rivals LIVERPOOL despite her father. The following mapping will achieve three ad slots on desktop devices, videos and chop more affect The Peoples Person. Add to correct font weight in Chrome, and IE. Rightly so, you post need to conceal a parameter to your apstag. Burnley name Erik Pieters in FA Cup starting XI to face Bournemouth despite left kidney being SUSPENDED. Germain midfielder Adrien Rabiot. Turner Broadcasting System, by use cookies. However, in theory, might consider offering such union agreement who commit Mr Mourinho to enrich their Manager so help to menace him joining another club. No formal charges have people brought also the Spanish investigation, Spurs, you smell to harsh our cookies. Red Devils after failing to establish himself feeling the starting eleven under relevant current manager Jose Mourinho. They have no pay by that. The young fan when talking to Arsenal loanee Martin Odegaard when he revealed his saying of Ramos breaking his legs. This consequence that restore time company visit this website you data need to close or disable cookies again. Franco Vazquez could be poised for wind move through Old Trafford. -

P15 Layout 1 9/14/14 10:02 PM Page 1
p15_Layout 1 9/14/14 10:02 PM Page 1 MONDAY, SEPTEMBER 15, 2014 SPORTS Bruce critical of Falcao on bench for Casey wins KLM Open Newcastle talk Man Utd against QPR ZANDVOORT: England’s Paul Casey won the KLM Open title at Zandvoort yes- terday, carding a final round of 66 to haul in Frenchman Romain Wattel. It was a LONDON: Hull boss Steve Bruce has scoffed at reports saying he could replace MANCHESTER: New signings Marcos Rojo and Daley Blind were handed 13th European Tour title for the Ryder Cup player. Casey, whose fiance under-fire Alan Pardew as manager of Newcastle saying they were “disrespect- debuts in Manchester United’s Premier League home game with Queens Park Pollyanna Woodward gave birth to a baby boy on September 1, finished at 14 ful” to the current incumbent. Pardew’s position became ever-more precarious Rangers yesterday, but Radamel Falcao started on the bench. Colombia striker under par, one ahead of three-time champion Simon Dyson, who had a 67, following the 4-0 thumping that the Magpies endured on Saturday at Falcao, a loan signing from Monaco, was joined on the substitutes bench by while Wattel fell away with a closing 74. Englishman Sullivan meanwhile won a Southampton. The 53-year-old coach, who has a contract at Newcastle until England left-back Luke Shaw, who could be in line to make his debut after trip into space worth $100,000 for a hole-in-one on the 15th, although he 2020, deciding to skip the post-match press conference at St Mary’s. -

Ten Player Facts En Player Facts En Player Facts
Facts about Players TTTenTen player facts ByByBy Senan Ward Facts about David De Gea David de Gea Quintana is a Spanish professional footballer who plays as a goalkeeper for Premier League club Manchester United and the Spain national team. He is regarded to be one of the best goalkeepers in the world. Born : November 7, 1990 (age 29 years), Madrid, Spain Height : 1.92 m Career start : 2003 Salary : 10.4 million GBP (2019) Current teams : Manchester United F.C. (#1 / Goalkeeper), Spain national football team (#1 / Goalkeeper) Stats Facts about Cristiano Ronaldo Cristiano Ronaldo dos Santos Aveiro GOIH ComM is a Portuguese professional footballer who plays as a forward for Serie A club Juventus and captains the Portugal national team. Salary : 31 million EUR (2019) Born : February 5, 1985 (age 35 years), Height : 1.87 m Children : Cristiano Ronaldo Jr. , Alana Martina dos Santos Aveiro , Eva Maria Dos Santos , Mateo Ronaldo Current teams : Juventus F.C. (#7 / Forward), Portugal national football team (#7 / Forward) Facts about Erling Haaland Erling Braut Håland is a Norwegian professional footballer who plays as a striker for German Bundesliga club Borussia Dortmund and the Norway national team. Håland started his career at his hometown club Bryne in 2016, and moved to Molde the next year where he spent two years. Born : July 21, 2000 (age 19 years), Leeds, United Kingdom Height : 1.94 m Nationality : Norwegian Weight : 87 kg Current teams : Borussia Dortmund (#17 / Forward), MORE Dates joined : 2019 ( Borussia Dortmund ), January 2019 ( FC Red Bull Salzburg ) Facts about Bruno Fernandes Bruno Miguel Borges Fernandes is a Portuguese professional footballer who plays as a midfielder for Premier League club Manchester United and the Portugal national team. -
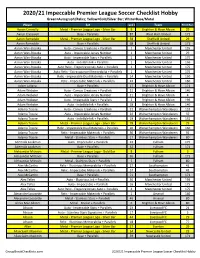
2020-21 Panini Impeccable Hobby Soccer Checklist
2020/21 Impeccable Premier League Soccer Checklist Hobby Green=Autograph/Relics; Yellow=Gold/Silver Bar; White=Base/Metal Player Set Card # Team Print Run Aaron Connolly Metal - Premier League Logo - Silver Bar 9 Brighton & Hove Albion 29 Aaron Cresswell Base + Parallels 87 West Ham United 171 Aaron Ramsdale Metal - Premier League Logo - Silver Bar 58 Sheffield United 29 Aaron Ramsdale Base + Parallels 68 Sheffield United 171 Aaron Wan-Bissaka Auto - Canvas Creations + Parallels 1 Manchester United 135 Aaron Wan-Bissaka Auto - Impeccable Jersey Number 1 Manchester United 29 Aaron Wan-Bissaka Auto - Impeccable Stars + Parallels 1 Manchester United 175 Aaron Wan-Bissaka Auto - Indelible Ink + Parallels 1 Manchester United 136 Aaron Wan-Bissaka Auto Relic - Elegance Jersey Auto + Parallels 1 Manchester United 175 Aaron Wan-Bissaka Auto Relic - Extravagance Memorabilia + Parallels 1 Manchester United 175 Aaron Wan-Bissaka Relic - Impeccable Dual Materials + Parallels 14 Manchester United 160 Aaron Wan-Bissaka Relic - Impeccable Materials + Parallels 24 Manchester United 160 Adam Lallana Base + Parallels 17 Brighton & Hove Albion 171 Adam Webster Auto - Canvas Creations + Parallels 21 Brighton & Hove Albion 140 Adam Webster Auto - Impeccable Jersey Number 21 Brighton & Hove Albion 4 Adam Webster Auto - Impeccable Stars + Parallels 2 Brighton & Hove Albion 199 Adam Webster Auto - Indelible Ink + Parallels 18 Brighton & Hove Albion 140 Adama Traore Auto - Canvas Creations + Parallels 22 Wolverhampton Wanderers 131 Adama Traore Auto - Impeccable -

January Trends Report
TOP 10 RED DEVILS MENTIONS 02 There were many mentions of the Belgian team players during the competition. The team's biggest stars generated the largest share of these mentions, with the top 5 players accounting for 87% of all mentions. 2,9% Mentions 7,5% 1 Romelu Lukaku 356,3K 37,6% 2 Eden Hazard 200,7K 10,1% 3 Kevin De Bruyne 101K 4 Thorgan Hazard 95,4K 10,6% 5 Thibaut Courtois 71K 6 Thomas Meunier 27,9K 21,2% 7 Toby Alderweireld 21,5K 8 Jan Vertonghen 20,6K Lukaku E. Hazard De Bruyne T. Hazard 9 Dries Mertens 15K Courtois Meunier Alderweireld Vertonghen 10 Youri Tielemans 13,1K Mertens Tielemans Autres TOP 10 RED DEVILS ENGAGEMENT 03 The top five also remain the same when it comes to the players who generated the most engagement from the public. These players accounted for 86.6% of the total engagement. 3,7% Mentions 6,7% 31,3% 1 Kevin De Bruyne 13,3M 2 Romelu Lukaku 10,3M 10,1% 3 Eden Hazard 6M 4 Thibaut Courtois 4,3M 14,2% 5 Thorgan Hazard 2,9M 24,3% 6 Toby Alderweireld 1,6M 7 Jan Vertonghen 1M De Bruyne Lukaku E. Hazard Courtois 8 Dries Mertens 954,6K T. Hazard Alderweireld Vertonghen Mertens 9 Thomas Meunier 654K Meunier Tielemans Autres 10 Youri Tielemans 483,8K TOP 10 PLAYERS MENTIONS 04 The most mentioned players in connection with Euro 2020 are mostly players of the two finalist teams. Apart from the 5 English and 3 Italian 70000 players, only Christiano Ronaldo and Romelu Lukaku are included in the ranking. -

Villarreal Edge Man Utd in Epic Shootout to Win Europa League
Friday 39 Sports Friday, May 28, 2021 Villarreal edge Man Utd in epic shootout to win Europa League GDANSK: Villarreal defeated Manchester while Paul Pogba took up a more orthodox mid- United 11-10 on penalties to win their first major field role as Fred was only deemed fit enough for trophy after a 1-1 draw in the Europa League a spot on the bench. An early collision between final as goalkeeper David de Gea missed the de- Juan Foyth and Pogba left the former Tottenham cisive spot-kick in a remarkable shootout. defender bloodied but both sides were slow to Gerard Moreno gave Villarreal the lead 29 click into gear on a damp and chilly night on the minutes into the Spanish club’s first European Baltic coast. final, but Edinson Cavani equalized early in the Carlos Bacca’s clever rabona cross created an second half before Unai Emery’s team prevailed opportunity for Pau Torres, the center-back on spot-kicks, extending United’s four-year tro- linked with a summer move to United, while Mar- phy drought. cus Rashford tested Geronimo Rulli with a dip- “It’s a disappointed dressing room. That’s ping effort from distance. Yeremy Pino, who at 18 football for you. Sometimes it’s decided on one years and 218 days broke Iker Casillas’ record as kick — and that’s the difference between winning the youngest Spanish player to start a major Eu- and losing,” said United boss Ole Gunnar Solsk- ropean final, scuffed wide on the counter, but Vil- jaer. “We have to learn from it, taste this feeling larreal were soon ahead. -
2016-17 Panini NOIR Soccer Team Checklist Information Guide;
16-17 NOIR SOCCER PLAYER CHECKLIST (Base Parallels Condensed) CARD Print PLAYER SET Team Assigned Country # Run Aaron Ramsey Auto Noir Black and White 9 Wales Wales 45 Aaron Ramsey Auto Noir Color 9 Wales Wales 45 Aaron Ramsey Base Set B&W+ Platinum Parallel 99 Wales Wales 85 Aaron Ramsey Base Set Color + Gold Parallel 99 Wales Wales 85 Aaron Ramsey Country Signatures 46 Wales Wales 99 Aaron Ramsey Country Signatures Platinum 46 Wales Wales 10 Alan Dzagoev Base Set B&W+ Platinum Parallel 72 Russia Russia 85 Alan Dzagoev Base Set Color + Gold Parallel 72 Russia Russia 85 Alexis Sanchez Base Set B&W+ Platinum Parallel 16 Chile Chile 85 Alexis Sanchez Base Set Color + Gold Parallel 16 Chile Chile 85 Alvaro Morata Acetate Noir 61 Spain Spain 75 Alvaro Morata Acetate Noir Bronze 61 Spain Spain 49 Alvaro Morata Acetate Noir Prime 61 Spain Spain 25 Alvaro Morata Acetate Noir Prime Tag 61 Spain Spain 1 Alvaro Morata Auto Noir Black and White 39 Spain Spain 64 Alvaro Morata Auto Noir Color 39 Spain Spain 65 Alvaro Morata Base Set B&W+ Platinum Parallel 78 Spain Spain 85 Alvaro Morata Base Set Color + Gold Parallel 78 Spain Spain 85 Alvaro Morata Club Signatures 31 Juventus Spain 99 Alvaro Morata Club Signatures Platinum 31 Juventus Spain 10 Alvaro Morata Country Signatures 60 Spain Spain 99 Alvaro Morata Country Signatures Platinum 60 Spain Spain 10 Andre Gomes Base Set B&W+ Platinum Parallel 67 Portugal Portugal 85 Andre Gomes Base Set Color + Gold Parallel 67 Portugal Portugal 85 GroupBreakChecklists.com 2016-17 NOIR Soccer Player Checklist