DOCSLIB.ORG

Visualizing Mathematics with 3D Printing

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Visualizing Mathematics with 3D Printing Visualizing Mathematics with 3D Printing job: 3D数学 内文 pi 160427 jun This page intentionally left blank Visualizing Mathematics with 3D Printing HENRY SEGERMAN JOHNS HOPKINS UNIVERSITY PRESS BALTIMORE job: 3D数学 内文 piii 160427 jun © 2016 Johns Hopkins University Press All rights reserved. Published 2016 Printed in China on acid-free paper 9 8 7 6 5 4 3 2 1 Johns Hopkins University Press 2715 North Charles Street Baltimore, Maryland 21218-4363 www.press.jhu.edu Library of Congress Cataloging-in-Publication Data Names: Segerman, Henry, 1979– Title: Visualizing mathematics with 3D printing / Henry Segerman. Description: Baltimore : Johns Hopkins University Press, 2016. | Includes bibli- ographical references and index. Identifi ers: LCCN 2015043848| ISBN 9781421420356 (hardcover : alk. paper) | ISBN 9781421420363 (electronic) | ISBN 142142035X (hardcover : alk. paper) | ISBN 1421420368 (electronic) Subjects: LCSH: Geometry—Computer-assisted instruction. | Mathemat- ics—Computer-assisted instruction. | Geometry—Study and teaching. | Geometrical constructions. | Three-dimensional imaging. | Three-dimen- sional printing. Classifi cation: LCC QA462.2.C65 S44 2016 | DDC 516.028/6—dc23 LC record available at http://lccn.loc.gov/2015043848 A catalog record for this book is available from the British Library. Special discounts are available for bulk purchases of this book. For more informa- tion, please contact Special Sales at 410-516-6936 or [email protected]. Johns Hopkins University Press uses environmentally friendly book mate- rials, including recycled text paper that is composed of at least 30 percent post-consumer waste, whenever possible. job: 3D数学 内文 piv 160427 jun Contents Preface vii Acknowledgments xi 1 Symmetry 1 2 Polyhedra 23 3 Four-Dimensional Space 33 4 Tilings and Curvature 69 5 Knots 97 6 Surfaces 111 7 Menagerie 149 Appendix A: Commentary on Figures 159 Appendix B: How I Made These Models 177 Index 181 n job: 3D数学 内文 pv 160427 jun This page intentionally left blank Preface Welcome to my book, dear reader. Before anything else, let me fi rst encourage you to visit the companion website to this book, 3dprintmath.com. This is a popular mathematics book, intended for everyone, no matter his or her mathematical level. This book is a little diff erent from other popular math or science books. In this book, whenever it makes sense, the diagrams are photographs of real-life 3D printed models. Almost all of these models are avail- able virtually on the website—they can be rotated around on the screen so that you can view them from any angle. They are also available to download and 3D print on your own 3D printer or purchase online at the website. With these models, you, the reader, can experi- ence three-dimensional concepts directly, as three- dimensional objects. They let me describe some very beautiful mathematics, including some topics that, although accessible, are diffi cult to explain well using only two-dimensional images. I’ve tried hard to make things understandable with only the book, but ideally you should be reading while holding the 3D printed diagrams in your hands or using the virtual models on the website. Because this book is built around 3D printed diagrams, the topics we will look at tend toward the geometric. The fi rst chapter is about the diff erent ways that three-dimensional objects can be symmetric. Chapter 2 is about some of the simplest shapes: the two-dimensional polygons and the polyhedra, their three-dimensional relatives. Chapter 3 builds off chap- ter 2, reaching up to the four-dimensional relatives vii n job: 3D数学 内文 pvii 160427 jun of polygons and polyhedra and investigating how we can see four-dimensional objects by casting shadows of them down to three dimensions. Chapter 4 is about tilings and curvature—whether a surface is shaped like a hill, a fl at plane, or a saddle. Chapter 5 is about knots and thinking topologically—looking at geomet- ric objects but not caring about the precise shapes, as if everything were made of very stretchy rubber. Chapter 6 continues the topological theme by looking at surfaces and then later on thinking about geome- try again by putting tilings on surfaces. Chapter 7 is a menagerie, of mathematical prints I couldn’t resist including in the book. Appendix A lists credits and technical details for the fi gures and 3D prints. Some of these include parametric equations that the adventurous reader may want to use to create her own visualizations. If you’re interested in how I go about making models, see appendix B. There isn’t much in the way of tricky notation or calculations in this book. It’s more about getting a visual sense of what’s going on. Having said that, some things might be a bit diffi cult to follow. If you get stuck on something, feel absolutely free to skip over it and come back later. Why 3D printing? 3D printing is a technology that gives unprecedented freedom in the creation of three-dimensional physical objects. A 3D printer builds an object layer by layer in an automated addi- tive process, based on a design given to it by a com- puter. 3D printers are particularly suited to producing mathematically inspired objects, in part because designs can be generated by programs written to pre- cisely represent the mathematics. Because production is automated, the physical models you obtain closely approximate the mathematical ideals. Small produc- tion runs of 3D objects and production on demand aren’t as possible with other manufacturing technol- ogies. There’s no way I could have made all of the diagrams in this book without 3D printing. One last comment before we get started: 3D print- viii Preface job: 3D数学 内文 pviii 160427 jun ers are so good at producing mathematical models that I sometimes run into an interesting problem. A photograph of a physical 3D printed object is so close to the mathematical ideal that viewers sometimes assume that the photograph is actually a computer render. All of the pictures in this book that look like photographs of real objects are indeed photographs of real objects, sometimes with some color added to the image to highlight a feature. I have deliberately left occasional imperfections in the photographs to prove their reality. Or at least, this seems like an excellent excuse/reason for any fl aws you may fi nd. ix Preface un job: 3D数学 内文 pix 160427 jun This page intentionally left blank Acknowledgments This book would not have happened without many, many other people. First of all, my parents, Eph and Jil Segerman, were instrumental in my existence. Ap- parently, they also had a large part to play in getting me into 3D stuff in the fi rst place, because both my brother, Will, and I have (in very diff erent ways) built our careers around 3D. Will’s current main source of income is as a virtual milliner. Make of that what you will. Huge thanks to my various collaborators. My brother, Will, worked with me on the monkey sculp- tures, and Vi Hart got us thinking about four-dimen- sional symmetries. Keenan Crane fl owed a coff ee mug, Geoff rey Irving fi gured out where to put hinged triangles, Craig S. Kaplan tiled a bunny, Marco Mahler worked with me on mobiles, and Roice Nelson tiled two- and three-dimensional hyperbolic space. Par- ticular thanks to Saul Schleimer, my collaborator in both topology research and mathematical illustration, who is very easy to distract from the former to the latter. Saul and I worked on too many projects to list here, apart from the one with yet another collabora- tor: the parametrization of the fi gure-eight knot, with François Guéritaud. Thanks to the other mathematicians, designers, and artists whose work I featured: Vladimir Bulatov, Bathsheba Grossman, George Hart, Oliver Labs, Carlo Séquin, Laura Taalman, Oskar van Deventer; Jessica Rosenkrantz and Jesse Louis-Rosenberg of Nervous System; the team that worked on the ropelength knots: Jason Cantarella, Eric Rawdon, Michael Piatek, and Ted Ashton; and the team that worked on the fl at xi job: 3D数学 内文 pxi 160427 jun torus: Vincent Borrelli, Saïd Jabrane, Francis Lazarus, and Boris Thibert. Thanks to Bus Jaco (the head of) and the rest of the Department of Mathematics at Oklahoma State University, for their support while I was writing the book. Bus helped me track down the OSU physics and chemistry instrument shop that built the photo rig for me and also found Joyce Lucca and Sam Welch, who loaned me the turntable. The purchases of many of the models were supported by a Dean’s Incentive Grant from the College of Arts and Sciences at OSU. Thanks to Robert McNeel & Associates for making Rhinoceros, the main program I used to design the models, and to the 3D printing service Shapeways for printing them. Jarey Shay designed the companion website to the book, and NeilFred Picciotto acquired the domain names. Stephan Tillmann and an anonymous reviewer both made early suggestions that changed the core focus of the book. I had some useful conversations about nega- tively curved spaces with Chaim Goodman-Strauss. Thanks to Vincent J. Burke, Andre M. Barnett, and everyone else at Johns Hopkins University Press, who turned my manuscript into a book. Moira Bucciarelli, Evelyn Lamb, Craig Kaplan, Rick Rubinstein, Saul Schleimer, Jil Segerman, Carlo Séquin, Rosa Zwier, and the anonymous reviewers read through versions of the book and found lots of ways to make it better and clearer. All errors are, of course, my own. xii Acknowledgments job: 3D数学 内文 pxii 160427 jun Visualizing Mathematics with 3D Printing n job: 3D数学 内文 pxiii 160427 jun This page intentionally left blank 1 Symmetry Symmetrical objects and patterns surround us, in art, architecture, and design.
Load more

Recommended publications
  • Arxiv:Math/9807161V1
    FOUR OBSERVATIONS ON n-TRIVIALITY AND BRUNNIAN LINKS Theodore B. Stanford Mathematics Department United States Naval Academy 572 Holloway Road Annapolis, MD 21402 [email protected] Abstract. Brunnian links have been known for a long time in knot theory, whereas the idea of n-triviality is a recent innovation. We illustrate the relationship between the two concepts with four short theorems. In 1892, Brunn introduced some nontrivial links with the property that deleting any single component produces a trivial link. Such links are now called Brunnian links. (See Rolfsen [7]). Ohyama [5] introduced the idea of a link which can be independantly undone in n different ways. Here “undo” means to change some set of crossings to make the link trivial. “Independant” means that once you change the crossings in any one of the n sets, the link remains trivial no matter what you do to the other n − 1 sets of crossings. Philosophically, the ideas are similar because, after all, once you delete one component of a Brunnian link the result is trivial no matter what you do to the other components. We shall prove four theorems that make the relationship between Brunnian links and n-triviality more precise. We shall show (Theorem 1) that an n-component Brunnian link is (n − 1)-trivial; (Theorem 2) that an n-component Brunnian link with a homotopically trivial component is n-trivial; (Theorem 3) that an (n − k)-component link constructed from an n-component Brunnian link by twisting along k components is (n − 1)-trivial; and (Theorem 4) that a knot is (n − 1)-trivial if and only if it is “locally n-Brunnian equivalent” to the unknot.
    [Show full text]
  • Arxiv:1601.05292V3 [Math.GT] 28 Mar 2017
    LINK HOMOTOPIC BUT NOT ISOTOPIC BAKUL SATHAYE Abstract. Given an m-component link L in S3 (m ≥ 2), we construct a family of links which are link homotopic, but not link isotopic, to L. Every proper sublink of such a link is link isotopic to the corresponding sublink of L. Moreover, if L is an unlink then there exist links that in addition to the above properties have all Milnor invariants zero. 1. Introduction 3 1 3 An n-component link L in S is a collection of piecewise linear maps (l1; : : : ; ln): S ! S , 1 1 where the images l1(S ); : : : ; ln(S ) are pairwise disjoint. A link with one component is a knot. 3 Two links in S , L1 and L2, are said to be isotopic if there is an orientation preserving homeo- 3 3 morphism h : S ! S such that h(L1) = L2 and h is isotopic to the identity map. The notion of link homotopy was introduced by Milnor in [4]. Two links L and L0 are said 0 to be link homotopic if there exist homotopies hi;t, between the maps li and the maps li so that 1 1 the sets h1;t(S ); : : : ; hn;t(S ) are disjoint for each value of t. In particular, a link is said to be link homotopically trivial if it is link homotopic to the unlink. Notice that this equivalence allows self-crossings, that is, crossing changes involving two strands of the same component. The question that arises now is: how different are these two notions of link equivalence? From the definition it is clear that a link isotopy is a link homotopy as well.
    [Show full text]
  • Knots, Molecules, and the Universe: an Introduction to Topology
    KNOTS, MOLECULES, AND THE UNIVERSE: AN INTRODUCTION TO TOPOLOGY AMERICAN MATHEMATICAL SOCIETY https://doi.org/10.1090//mbk/096 KNOTS, MOLECULES, AND THE UNIVERSE: AN INTRODUCTION TO TOPOLOGY ERICA FLAPAN with Maia Averett David Clark Lew Ludwig Lance Bryant Vesta Coufal Cornelia Van Cott Shea Burns Elizabeth Denne Leonard Van Wyk Jason Callahan Berit Givens Robin Wilson Jorge Calvo McKenzie Lamb Helen Wong Marion Moore Campisi Emille Davie Lawrence Andrea Young AMERICAN MATHEMATICAL SOCIETY 2010 Mathematics Subject Classification. Primary 57M25, 57M15, 92C40, 92E10, 92D20, 94C15. For additional information and updates on this book, visit www.ams.org/bookpages/mbk-96 Library of Congress Cataloging-in-Publication Data Flapan, Erica, 1956– Knots, molecules, and the universe : an introduction to topology / Erica Flapan ; with Maia Averett [and seventeen others]. pages cm Includes index. ISBN 978-1-4704-2535-7 (alk. paper) 1. Topology—Textbooks. 2. Algebraic topology—Textbooks. 3. Knot theory—Textbooks. 4. Geometry—Textbooks. 5. Molecular biology—Textbooks. I. Averett, Maia. II. Title. QA611.F45 2015 514—dc23 2015031576 Copying and reprinting. Individual readers of this publication, and nonprofit libraries acting for them, are permitted to make fair use of the material, such as to copy select pages for use in teaching or research. Permission is granted to quote brief passages from this publication in reviews, provided the customary acknowledgment of the source is given. Republication, systematic copying, or multiple reproduction of any material in this publication is permitted only under license from the American Mathematical Society. Permissions to reuse portions of AMS publication content are handled by Copyright Clearance Center’s RightsLink service.
    [Show full text]
  • Brunnian Weavings
    Bridges 2010: Mathematics, Music, Art, Architecture, Culture Brunnian Weavings Douglas G. Burkholder Donald & Helen Schort School of Mathematics & Computing Sciences Lenoir-Rhyne College 625 7th Avenue NE Hickory, North Carolina, 28601 E-mail: [email protected] Abstract In this paper, we weave Borromean Rings to create interesting objects with large crossing number while retaining the characteristic property of the Borromean Rings. Borromean Rings are interesting because they consist of three rings linked together and yet when any single ring is removed the other two rings become unlinked. The first weaving applies an iterative self-similar technique to produce an artistically interesting weaving of three rings into a fractal pattern. The second weaving uses an iterative Peano Curve technique to produce a tight weaving over the surface of a sphere. The third weaving produces a tight weaving of four rings over the surface of a torus. All three weavings can produce links with an arbitrarily large crossing number. The first two procedures produce Brunnian Links which are links that retain the characteristic property of the Borromean Rings. The third produces a link that retains some of the characteristics Borromean Rings when perceived from the surface of a torus. 1. Borromean Rings and Brunnian Links Our goal is to create interesting Brunnian Weavings with an arbitrarily large crossing number. The thought in this paper is that Borromean Rings become more interesting as they become more intertwined. Borromean Rings consist of three rings linked together and yet when any single ring is removed the other two rings become unlinked. Figure 1.1 shows the most common representation of the Borromean Rings.
    [Show full text]
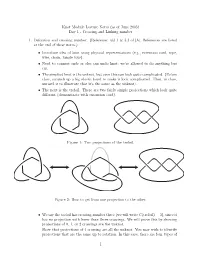
  • Knot Module Lecture Notes (As of June 2005) Day 1 - Crossing and Linking Number
    Knot Module Lecture Notes (as of June 2005) Day 1 - Crossing and Linking number 1. Definition and crossing number. (Reference: §§1.1 & 3.3 of [A]. References are listed at the end of these notes.) • Introduce idea of knot using physical representations (e.g., extension cord, rope, wire, chain, tangle toys). • Need to connect ends or else can undo knot; we’re allowed to do anything but cut. • The simplest knot is the unknot, but even this can look quite complicated. (Before class, scrunch up a big elastic band to make it look complicated. Then, in class, unravel it to illustrate that it’s the same as the unknot). • The next is the trefoil. There are two fairly simple projections which look quite different (demonstrate with extension cord). Figure 1: Two projections of the trefoil. Figure 2: How to get from one projection to the other. • We say the trefoil has crossing number three (we will write C(trefoil) = 3), since it has no projection with fewer than three crossings. We will prove this by showing projections of 0, 1, or 2 crossings are the unknot. Show that projections of 1 crossing are all the unknot. You may wish to identify projections that are the same up to rotation. In this case, there are four types of 1 Figure 3: Some 1-crossing projections. 1-crossing projection. If you also allow reflections, then there are only two types, one represented by the left column of Figure 3 and the other by any of the eight other projections. The crossing number two case is homework.
    [Show full text]
  • Detecting Linkage in an N-Component Brunnian Link (Work in Progress)
    Detecting Linkage in an n-Component Brunnian Link (work in progress) Ron Umble, Barbara Nimershiem, and Merv Fansler Millersville U and Franklin & Marshall College Tetrahedral Geometry/Topology Seminar December 4, 2015 Tetrahedral Geometry/Topology Seminar ( DetectingTetrahedral Brunnian Geometry/Topology Linkage Seminar ) December4,2015 1/28 Ultimate Goal of the Project Computationally detect the linkage in an n-component Brunnian link Tetrahedral Geometry/Topology Seminar ( DetectingTetrahedral Brunnian Geometry/Topology Linkage Seminar ) December4,2015 2/28 Review of Cellular Complexes Let X be a connected network, surface, or solid embedded in S3 Tetrahedral Geometry/Topology Seminar ( DetectingTetrahedral Brunnian Geometry/Topology Linkage Seminar ) December4,2015 3/28 closed intervals (edges or 1-cells) closed disks (faces or 2-cells) closed balls (solids or 3-cells) glued together so that the non-empty boundary of a k-cell is a union of (k 1)-cells non-empty intersection of cells is a cell union of all cells is X Cellular Decompositions A cellular decomposition of X is a finite collection of discrete points (vertices or 0-cells) Tetrahedral Geometry/Topology Seminar ( DetectingTetrahedral Brunnian Geometry/Topology Linkage Seminar ) December4,2015 4/28 closed disks (faces or 2-cells) closed balls (solids or 3-cells) glued together so that the non-empty boundary of a k-cell is a union of (k 1)-cells non-empty intersection of cells is a cell union of all cells is X Cellular Decompositions A cellular decomposition of X is a finite
    [Show full text]
  • Master Thesis Supervised by Dr
    THE RASMUSSEN INVARIANT OF ARBORESCENT AND OF MUTANT LINKS LUKAS LEWARK master of science eth in mathematics master thesis supervised by dr. sebastian baader Abstract. In the first section, an account of the definition and basic prop- erties of the Rasmussen invariant for knots and links is given. An inequality involving the number of positive Seifert circles of a link diagram, originally due to Kawamura, is proven. In the second section, arborescent links are intro- duced as links arising from plumbing twisted bands along a tree. An algorithm to calculate their signature is given, and, using the inequality mentioned above, their Rasmussen invariant is computed. In the third section, an account of the concept of mutant links is given and an upper bound for the difference of the Rasmussen invariants of two mutant links is proven. Contents Introduction 2 I. The Rasmussen invariant 3 I.1. Filtered vector spaces 3 I.2. The Khovanov-Lee complex 6 I.3. Cobordisms and definition of the Rasmussen invariant s for links 9 I.4. Basic properties of s 13 I.5. An inequality involving the number of positive circles 16 I.6. The relationship of the signature and s 18 II. Arborescent links 20 II.1. Definition and basic properties of arborescent links 20 II.2. The signature of arborescent links 22 II.3. The Rasmussen invariant of arborescent links 24 III. Mutant links 26 III.1. Definition of mutant links 26 III.2. Behaviour of the Rasmussen invariant under mutation 27 Conclusion: Results and open problems 29 References 30 Date: April 11th, 2009.
    [Show full text]
  • Intelligence of Low Dimensional Topology 2006 : Hiroshima, Japan
    INTELLIGENCE OF LOW DIMENSIONAL TOPOLOGY 2006 SERIES ON KNOTS AND EVERYTHING Editor-in-charge: Louis H. Kauffman (Univ. of Illinois, Chicago) The Series on Knots and Everything: is a book series polarized around the theory of knots. Volume 1 in the series is Louis H Kauffman’s Knots and Physics. One purpose of this series is to continue the exploration of many of the themes indicated in Volume 1. These themes reach out beyond knot theory into physics, mathematics, logic, linguistics, philosophy, biology and practical experience. All of these outreaches have relations with knot theory when knot theory is regarded as a pivot or meeting place for apparently separate ideas. Knots act as such a pivotal place. We do not fully understand why this is so. The series represents stages in the exploration of this nexus. Details of the titles in this series to date give a picture of the enterprise. Published: Vol. 1: Knots and Physics (3rd Edition) by L. H. Kauffman Vol. 2: How Surfaces Intersect in Space — An Introduction to Topology (2nd Edition) by J. S. Carter Vol. 3: Quantum Topology edited by L. H. Kauffman & R. A. Baadhio Vol. 4: Gauge Fields, Knots and Gravity by J. Baez & J. P. Muniain Vol. 5: Gems, Computers and Attractors for 3-Manifolds by S. Lins Vol. 6: Knots and Applications edited by L. H. Kauffman Vol. 7: Random Knotting and Linking edited by K. C. Millett & D. W. Sumners Vol. 8: Symmetric Bends: How to Join Two Lengths of Cord by R. E. Miles Vol. 9: Combinatorial Physics by T.
    [Show full text]
  • Knots, Lassos, and Links
    KNOTS, LASSOS, AND LINKS pawełdabrowski˛ -tumanski´ Topological manifolds in biological objects June 2019 – version 1.0 [ June 25, 2019 at 18:23 – classicthesis version 1.0 ] PawełD ˛abrowski-Tuma´nski: Knots, lassos, and links, Topological man- ifolds in biological objects, © June 2019 Based on the ClassicThesis LATEXtemplate by André Miede. [ June 25, 2019 at 18:23 – classicthesis version 1.0 ] To my wife, son, and parents. [ June 25, 2019 at 18:23 – classicthesis version 1.0 ] [ June 25, 2019 at 18:23 – classicthesis version 1.0 ] STRESZCZENIE Ła´ncuchybiałkowe opisywane s ˛azazwyczaj w ramach czterorz ˛edowej organizacji struktury. Jednakze,˙ ten sposób opisu nie pozwala na uwzgl ˛ednienieniektórych aspektów geometrii białek. Jedn ˛az braku- j ˛acych cech jest obecno´s´cw˛ezła stworzonego przez ła´ncuchgłówny. Odkrycie białek posiadaj ˛acych taki w˛ezełbudzi pytania o zwijanie takich białek i funkcj ˛ew˛ezła. Pomimo poł˛aczonegopodej´sciateore- tycznego i eksperymentalnego, odpowied´zna te pytania nadal po- zostaje nieuchwytna. Z drugiej strony, prócz zaw˛e´zlonych białek, w ostatnich czasach zostały zidentyfikowane pojedyncze struktury zawie- raj ˛aceinne, topologicznie nietrywialne motywy. Funkcja tych moty- wów i ´sciezka˙ zwijania białek ich zawieraj ˛acych jest równiez˙ nieznana w wi ˛ekszo´sciprzypadków. Ta praca jest pierwszym holistycznym podej´sciemdo całego tematu nietrywialnej topologii w białkach. Prócz białek z zaw˛e´zlonymła´ncu- chem głównym, praca opisuje takze˙ inne motywy: białka-lassa, sploty, zaw˛e´zlonep ˛etlei ✓-krzywe. Niektóre spo´sród tych motywów zostały odkryte w ramach pracy. Wyniki skoncentrowano na klasyfikacji, wys- t ˛epowaniu, funkcji oraz zwijaniu białek z topologicznie nietrywial- nymi motywami. W cz ˛e´scipo´swi˛econejklasyfikacji, zaprezentowane zostały wszys- tkie topologicznie nietrywialne motywy wyst ˛epuj˛acew białkach.
    [Show full text]
  • A GENERALIZATION of MILNOR's Pinvariants to HIGHER
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Pergamon Topology Vol. 36, No. 2, pp. 301-324, 1997 Copyrigt 6 1996 Elsevier Science Ltd Printed in Great Britain. All rights reserved 004&9383/96 $15.00 + 0.00 SOO40-93tt3(96)00018-3 A GENERALIZATION OF MILNOR’S pINVARIANTS TO HIGHER-DIMENSIONAL LINK MAPS ULRICH KOSCHORKE~ (Receivedfor publication 26 March 1996) In this paper we generalize Milnor’s p-invariants (which were originally defined for “almost trivial” classical links in R3) to (a corresponding large class of) link maps in arbitrary higher dimensions. The resulting invariants play a central role in link homotopy classification theory. They turn out to be often even compatible with singular link concordances. Moreover, we compare them to linking coefficients of embedded links and to related invariants of Turaev and Nezhinskij. Along the way we also study certain auxiliary but important “Hopf homomorphisms”. Copyright 0 1996 Elsevier Science Ltd 1. INTRODUCTION Given r > 2 and arbitrary dimensions pl, . , p, 2 0 and m > 3, we want to study (spherical) link maps f=flJJ . ufr:S”lu .*. ~SP~-dP (1) (i.e. the continuous component maps fi have pairwise disjoint images) up to link homotopy, i.e. up to continuous deformations through such link maps. In other words, two link maps f and f’ are called link homotopic if there is a continuous map F =F,U . UFr: I) SP’XZ-+RrnXZ (2) i=l such that (i) Fi and Fj have disjoint images for 1 < i <j < r; (ii) F(x, 0) = (f(x), 0) and F(x, 1) = (f’(x), 1) for all x E JJ Spi; and (iii) F preserves Z-levels.
    [Show full text]
  • Milnor's Invariants and Self
    PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 137, Number 2, February 2009, Pages 761–770 S 0002-9939(08)09521-X Article electronically published on August 28, 2008 MILNOR’S INVARIANTS AND SELF Ck-EQUIVALENCE THOMAS FLEMING AND AKIRA YASUHARA (Communicated by Daniel Ruberman) Abstract. It has long been known that a Milnor invariant with no repeated index is an invariant of link homotopy. We show that Milnor’s invariants with repeated indices are invariants not only of isotopy, but also of self Ck- equivalence. Here self Ck-equivalence is a natural generalization of link homo- topy based on certain degree k clasper surgeries, which provides a filtration of link homotopy classes. 1. Introduction In his landmark 1954 paper [8], Milnor introduced his eponymous higher order linking numbers. For an n-component link, Milnor numbers are specified by a multi-index I, where the entries of I are chosen from {1,...,n}. In the paper [8], Milnor proved that when the multi-index I has no repeated entries, the numbers µ(I) are invariants of link homotopy. In a follow-up paper [9], Milnor explored some of the properties of the other numbers and showed they are invariant under isotopy, but not link homotopy. Milnor’s invariants have been connected with finite-type invariants, and the con- nection between them is increasingly well understood. For string links, these in- variants are known to be of finite-type [1, 6], and in fact related to (the tree part of) the Kontsevich integral in a natural and beautiful way [4]. By work of Habiro [5], the finite-type invariants of knots are intimately related to clasper surgery.
    [Show full text]
  • Brunnian Spheres
    Brunnian Spheres Hugh Nelson Howards 1. INTRODUCTION. Can the link depicted in Figure 1 be built out of round circles in 3-space? Surprisingly, although this link appears to be built out of three round circles, a theorem of Michael Freedman and Richard Skora (Theorem 2.1) proves that this must be an optical illusion! Although each component seems to be a circle lying in a plane, it is only the projection that is composed of circles and at least one of these components is bent in 3-space. Figure 1. The Borromean Rings are a Brunnian link. In this article we shed new light on the Freedman and Skora result that shows that no Brunnian link can be constructed of round components. We then extend it to two different traditional generalizations of Brunnian links. Recall that a “knot” is a subset of R3 that is homeomorphic to a circle (also called a 1-sphere or S1). Informally, a knot is said to be an “unknot” if it can be deformed through space to become a perfect (round) circle without ever passing through itself (see Figure 2); otherwise it is knotted (see Figure 3). Figure 2. The figure on the left is an unknot because it can be straightened to look like the figure on the right without introducing any self-intersections. A “link” L is just a collection of disjoint knots. A link L is an “unlink” of n com- ponents if it consists of n unknots and if the components can be separated without passing through each other (more rigorous definitions are given in section 3).
    [Show full text]