DOCSLIB.ORG

Black Hole Shadow with a Cosmological Constant for Cosmological Observers

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Black Hole Shadow with a Cosmological Constant for Cosmological Observers Eur. Phys. J. C (2019) 79:930 https://doi.org/10.1140/epjc/s10052-019-7464-2 Regular Article - Theoretical Physics Black hole shadow with a cosmological constant for cosmological observers Javad T. Firouzjaee1,2,a, Alireza Allahyari3,b 1 Department of Physics, K.N. Toosi University of Technology, P.O. Box 15418-49611, Tehran, Iran 2 School of Physics, Institute for Research in Fundamental Sciences (IPM), P. O. Box 19395-5531, Tehran, Iran 3 School of Astronomy, Institute for Research in Fundamental Sciences (IPM), P. O. Box 19395-5531, Tehran, Iran Received: 24 June 2019 / Accepted: 6 November 2019 / Published online: 15 November 2019 © The Author(s) 2019 Abstract Weinvestigate the effect of the cosmological con- cosmological expansion [12]. Motivated by the accelerated stant on the angular size of a black hole shadow. It is known expansion of the universe, we seek to investigate the effect that the accelerated expansion which is created by the cos- of the cosmological constant on the shadow shape. mological constant changes the angular size of the black hole Dark energy, one of the most important problems in cos- shadow for static observers. However, the shadow size must mology, is assumed to drive the current cosmic acceler- be calculated for the appropriate cosmological observes. We ated expansion. The cosmological constant, , is among calculate the angular size of the shadow measured by cosmo- the favored candidates responsible for this acceleration. The logical comoving observers by projecting the shadow angle cosmological constant has imprints on various phenomena to this observer rest frame. We show that the shadow size in structure formation and astrophysics. These effects can tends to zero as the observer approaches the cosmological appear as the integrated Sachs-Wolfe effect in the Cosmic horizon. We estimate the angular size of the shadow for a Microwave Background and large scale structure observ- typical supermassive black hole, e.g M87. It is found that the ables. Moreover, the cosmological constant can change the angular size of the shadow for cosmological observers and luminosity distance in the gravitational wave observations. static observers is approximately the same at these scales Recently, the role of the cosmological constant in gravita- of mass and distance. We present a catalog of supermassive tional lensing has been the subject of focused studies [13–22]. black holes and calculate the effect of the cosmological con- It seems there is no general agreement on the final results. The stant on their shadow size and find that the effect could be black hole shadow arises as a result of gravitational lensing in 3 precent for distant sources. strong gravity regime. Thus, one can investigate the influence of the cosmological constant on the shadow of black holes. The first attempt to derive the shadow size as measured by 1 Introduction the comoving observers was performed by Perlick et al. [23] using the Kottler metric. Authors in [12] presented an approx- Recent observations of black holes shadow at a wavelength imate method based on the angular size-redshift relation for of 1.3 mm spectrum succeeded in observing the first image of the general case of any multicomponent universe. Although the black hole in the center of the galaxy M87 [1,2]. Although the cosmological constant correction on the shadow shape of the first image of the black hole does not distinguish the black black holes has been studied in [24–27], choosing the appro- hole geometry precisely, the future improvement of measure- priate (cosmological) observers is another issue that one has ments will lead to a much higher resolution. This will allow to consider. us to study different aspects of cosmological black holes [3– Tostudy the effect of the cosmological constant in the lens- 8]. To this end, one needs to calculate the influence of dif- ing of a cosmological structure or shadow of a black hole, ferent parameters on the shape of cosmological (astrophys- one has to model a cosmological structure like a black hole in ical) black holes shadow, e.g accretion plasma effects [9], the expanding background. There have been many attempts semi-classical quantum effects [10], dark matter [11] and the to model a cosmological black hole (CBH). The authors in [3–8,30,31] have studied the effect of the expanding back- a e-mail: fi[email protected] ground. Since a cosmological structure like a galaxy, a cluster b e-mail: [email protected] of galaxies or a supermassive black hole in the center of a 123 930 Page 2 of 7 Eur. Phys. J. C (2019) 79 :930 quasar have dynamical evolution due to their dynamics or metric (1) will be written as cosmological expansion, one has to use a dynamical cosmo- 2M logical model to study its lensing [32,33]. It’s been shown ds2 =−dτ 2 + + R2 dr2 + R2d2. (4) [30,31] that the background expansion for CBHs leads to R 3 the formation of voids. These voids are formed between the We need to find R as a function of (r,τ). Using the coordinate black hole and the expanding background and prevent the transformation (3) yields black hole’s matter flux from increasing. After this phase of dR the black hole evolution, the black hole can be approximated τ + r = as a point mass [29]. As a result, the final stage of evolution R2 + 2M can be approximated by a point mass located in a dark energy 3 R 3 √ dominated background. 2 R 2 + 6M + 2 R3 = √ ln . (5) There is a well-known solution of the Einstein equation 3 κ for a point mass black hole in the presence of the cosmo- logical constant known as Schwarzschild-de Sitter/Kottler Solving Eq. (5) for R, we get spacetime. This solution is written in static coordinates. To √ 2 − (r+τ) ( +τ) 3 find the geodesic observers we have to apply an appropri- e 3 e 3 r κ2 − 6M = , ate coordinate transformation to present the Schwarzschild- R 2 (6) de Sitter/Kottler spacetime in the cosmological synchronous (2κ)3 gauge [28,29]. where κ is a constant. When M = 0, one can define a new This paper is organized as follows. In Sect. 2 we introduce radial coordinate as a point mass cosmological black hole. In Sect. 3, we calcu- late the angular size of the shadow in the Schwarzschild-de 2 κ 3 r R˜ = 3 . Sitter spacetime as measured by a cosmological comoving e (7) observer and calculate the different limits. The conclusion and discussion are given in Sect. 4. In this coordinate we obtain the de Sitter metric in the syn- chronous coordinates as 2 Point mass black holes metrics ds2 =−dτ 2 + a(τ)2 d R˜2 + R˜2 d2 , (8) It is known that the Schwarzschild-de Sitter is a standard met- τ ric for the CBH, but Schwarzschild-de Sitter has been written where a(τ) = e 3 . The four-velocity of the comoving in the static coordinates. To study the point mass metric in an observer, dr = 0, who measures the proper time τ can be expanding background, one needs to find the Schwarzschild- written using transformation (3) in the static coordinates as de Sitter metric in the cosmological coordinates. Since the √ standard cosmological metrics are written in the synchronous μ 1 U = , 1 − , 0, 0 , (9) coordinate, one has to transform the Schwarzschild-de Sitter to the synchronous coordinate [28,29]. The Schwarzschild- Four-acceleration of this observer is zero. Hence, it is called de Sitter metric in the static coordinates is given by the comoving cosmological observer. In contrast to the met- − ds2 =−dt2 + 1dR2 + R2 d2, (1) ric introduced in [23], the metric (4) is the appropriate met- ricinwhichr=constant world lines are attached to the where geodesic (comoving) observers. The position of each comov- 2M ing observer r = constant in static coordinates is given by = 1 − R2 − . (2) 3 R Eq. (6). In the next section, we calculate the angular shadow size seen by the cosmological comoving observers. 2 In the weak field limit, one can interpret 3 R as the cosmo- logical constant potential and compare it with the gravita- tional potential of the black hole, M/R for the gravitational 3 Shadow for cosmological comoving observer interactions. Using coordinate transformations √ 1 − Before calculating the angular size of the shadow for the dτ = dt − dR, cosmological observers, let us present the result for the static (3) dR observers from [23]. The shadow is locally seen by a static dr =−dt + √ , ( , ,θ = π/ ,φ = ) 1 − observer at a spacetime point tO RO O 2 O 0 123 Eur. Phys. J. C (2019) 79 :930 Page 3 of 7 930 outside the black hole horizon and inside the cosmologi- the photon trajectory denoted by d. In these coordinates, 1 2 cal horizon. The Lagrangian for geodesics in the equatorial δμ = ( , R , , ) dμ = kμ = L ER , A, , 0 o 0 0 and R2 L 0 1 where plane gives = dR A dφ on the null geodesics. As Ishak and Rindler have 1 R˙2 shown [14,15], one can calculate the bending angle using the L(x, x˙) = − (R)t˙2 + + R2φ˙2 . (10) 2 (R) invariant formula for the cosine of the angles between two directions d and δ. This gives The Euler–Lagrange equations for t and φ coordinates give two constants of motion, A cos ψ = √ , (17) E = (R) t˙, L = R2 φ˙ (11) A2 + R2 where E and L represent the energy and angular momentum where dot denotes the inner product. For the static observers of the geodesic. For null geodesics we have of the Schwartzchild-de Sitter spacetime, one can show ˙2 ˙2 R 2 ˙2 1 − 2M − R2 − (R) t + + R φ = 0.
Load more

Recommended publications
  • Astronomie in Theorie Und Praxis 8. Auflage in Zwei Bänden Erik Wischnewski
    Astronomie in Theorie und Praxis 8. Auflage in zwei Bänden Erik Wischnewski Inhaltsverzeichnis 1 Beobachtungen mit bloßem Auge 37 Motivation 37 Hilfsmittel 38 Drehbare Sternkarte Bücher und Atlanten Kataloge Planetariumssoftware Elektronischer Almanach Sternkarten 39 2 Atmosphäre der Erde 49 Aufbau 49 Atmosphärische Fenster 51 Warum der Himmel blau ist? 52 Extinktion 52 Extinktionsgleichung Photometrie Refraktion 55 Szintillationsrauschen 56 Angaben zur Beobachtung 57 Durchsicht Himmelshelligkeit Luftunruhe Beispiel einer Notiz Taupunkt 59 Solar-terrestrische Beziehungen 60 Klassifizierung der Flares Korrelation zur Fleckenrelativzahl Luftleuchten 62 Polarlichter 63 Nachtleuchtende Wolken 64 Haloerscheinungen 67 Formen Häufigkeit Beobachtung Photographie Grüner Strahl 69 Zodiakallicht 71 Dämmerung 72 Definition Purpurlicht Gegendämmerung Venusgürtel Erdschattenbogen 3 Optische Teleskope 75 Fernrohrtypen 76 Refraktoren Reflektoren Fokus Optische Fehler 82 Farbfehler Kugelgestaltsfehler Bildfeldwölbung Koma Astigmatismus Verzeichnung Bildverzerrungen Helligkeitsinhomogenität Objektive 86 Linsenobjektive Spiegelobjektive Vergütung Optische Qualitätsprüfung RC-Wert RGB-Chromasietest Okulare 97 Zusatzoptiken 100 Barlow-Linse Shapley-Linse Flattener Spezialokulare Spektroskopie Herschel-Prisma Fabry-Pérot-Interferometer Vergrößerung 103 Welche Vergrößerung ist die Beste? Blickfeld 105 Lichtstärke 106 Kontrast Dämmerungszahl Auflösungsvermögen 108 Strehl-Zahl Luftunruhe (Seeing) 112 Tubusseeing Kuppelseeing Gebäudeseeing Montierungen 113 Nachführfehler
    [Show full text]
  • The Global Jet Structure of the Archetypical Quasar 3C 273
    galaxies Article The Global Jet Structure of the Archetypical Quasar 3C 273 Kazunori Akiyama 1,2,3,*, Keiichi Asada 4, Vincent L. Fish 2 ID , Masanori Nakamura 4, Kazuhiro Hada 3 ID , Hiroshi Nagai 3 and Colin J. Lonsdale 2 1 National Radio Astronomy Observatory, 520 Edgemont Rd, Charlottesville, VA 22903, USA 2 Massachusetts Institute of Technology, Haystack Observatory, 99 Millstone Rd, Westford, MA 01886, USA; vfi[email protected] (V.L.F.); [email protected] (C.J.L.) 3 National Astronomical Observatory of Japan, 2-21-1 Osawa, Mitaka, Tokyo 181-8588, Japan; [email protected] (K.H.); [email protected] (H.N.) 4 Institute of Astronomy and Astrophysics, Academia Sinica, P.O. Box 23-141, Taipei 10617, Taiwan; [email protected] (K.A.); [email protected] (M.N.) * Correspondence: [email protected] Received: 16 September 2017; Accepted: 8 January 2018; Published: 24 January 2018 Abstract: A key question in the formation of the relativistic jets in active galactic nuclei (AGNs) is the collimation process of their energetic plasma flow launched from the central supermassive black hole (SMBH). Recent observations of nearby low-luminosity radio galaxies exhibit a clear picture of parabolic collimation inside the Bondi accretion radius. On the other hand, little is known of the observational properties of jet collimation in more luminous quasars, where the accretion flow may be significantly different due to much higher accretion rates. In this paper, we present preliminary results of multi-frequency observations of the archetypal quasar 3C 273 with the Very Long Baseline Array (VLBA) at 1.4, 15, and 43 GHz, and Multi-Element Radio Linked Interferometer Network (MERLIN) at 1.6 GHz.
    [Show full text]
  • Near-Infrared Luminosity Relations and Dust Colors L
    A&A 578, A47 (2015) Astronomy DOI: 10.1051/0004-6361/201525817 & c ESO 2015 Astrophysics Obscuration in active galactic nuclei: near-infrared luminosity relations and dust colors L. Burtscher1, G. Orban de Xivry1, R. I. Davies1, A. Janssen1, D. Lutz1, D. Rosario1, A. Contursi1, R. Genzel1, J. Graciá-Carpio1, M.-Y. Lin1, A. Schnorr-Müller1, A. Sternberg2, E. Sturm1, and L. Tacconi1 1 Max-Planck-Institut für extraterrestrische Physik, Postfach 1312, Gießenbachstr., 85741 Garching, Germany e-mail: [email protected] 2 Raymond and Beverly Sackler School of Physics & Astronomy, Tel Aviv University, 69978 Ramat Aviv, Israel Received 5 February 2015 / Accepted 5 April 2015 ABSTRACT We combine two approaches to isolate the AGN luminosity at near-IR wavelengths and relate the near-IR pure AGN luminosity to other tracers of the AGN. Using integral-field spectroscopic data of an archival sample of 51 local AGNs, we estimate the fraction of non-stellar light by comparing the nuclear equivalent width of the stellar 2.3 µm CO absorption feature with the intrinsic value for each galaxy. We compare this fraction to that derived from a spectral decomposition of the integrated light in the central arcsecond and find them to be consistent with each other. Using our estimates of the near-IR AGN light, we find a strong correlation with presumably isotropic AGN tracers. We show that a significant offset exists between type 1 and type 2 sources in the sense that type 1 MIR X sources are 7 (10) times brighter in the near-IR at log LAGN = 42.5 (log LAGN = 42.5).
    [Show full text]
  • Messier Objects
    Messier Objects From the Stocker Astroscience Center at Florida International University Miami Florida The Messier Project Main contributors: • Daniel Puentes • Steven Revesz • Bobby Martinez Charles Messier • Gabriel Salazar • Riya Gandhi • Dr. James Webb – Director, Stocker Astroscience center • All images reduced and combined using MIRA image processing software. (Mirametrics) What are Messier Objects? • Messier objects are a list of astronomical sources compiled by Charles Messier, an 18th and early 19th century astronomer. He created a list of distracting objects to avoid while comet hunting. This list now contains over 110 objects, many of which are the most famous astronomical bodies known. The list contains planetary nebula, star clusters, and other galaxies. - Bobby Martinez The Telescope The telescope used to take these images is an Astronomical Consultants and Equipment (ACE) 24- inch (0.61-meter) Ritchey-Chretien reflecting telescope. It has a focal ratio of F6.2 and is supported on a structure independent of the building that houses it. It is equipped with a Finger Lakes 1kx1k CCD camera cooled to -30o C at the Cassegrain focus. It is equipped with dual filter wheels, the first containing UBVRI scientific filters and the second RGBL color filters. Messier 1 Found 6,500 light years away in the constellation of Taurus, the Crab Nebula (known as M1) is a supernova remnant. The original supernova that formed the crab nebula was observed by Chinese, Japanese and Arab astronomers in 1054 AD as an incredibly bright “Guest star” which was visible for over twenty-two months. The supernova that produced the Crab Nebula is thought to have been an evolved star roughly ten times more massive than the Sun.
    [Show full text]
  • Star Maps: Where Are the Black Holes?
    BLACK HOLE FAQ’s 1. What is a black hole? A black hole is a region of space that has so much mass concentrated in it that there is no way for a nearby object to escape its gravitational pull. There are three kinds of black hole that we have strong evidence for: a. Stellar-mass black holes are the remaining cores of massive stars after they die in a supernova explosion. b. Mid-mass black hole in the centers of dense star clusters Credit : ESA, NASA, and F. Mirabel c. Supermassive black hole are found in the centers of many (and maybe all) galaxies. 2. Can a black hole appear anywhere? No, you need an amount of matter more than 3 times the mass of the Sun before it can collapse to create a black hole. 3. If a star dies, does it always turn into a black hole? No, smaller stars like our Sun end their lives as dense hot stars called white dwarfs. Much more massive stars end their lives in a supernova explosion. The remaining cores of only the most massive stars will form black holes. 4. Will black holes suck up all the matter in the universe? No. A black hole has a very small region around it from which you can't escape, called the “event horizon”. If you (or other matter) cross the horizon, you will be pulled in. But as long as you stay outside of the horizon, you can avoid getting pulled in if you are orbiting fast enough. 5. What happens when a spaceship you are riding in falls into a black hole? Your spaceship, along with you, would be squeezed and stretched until it was torn completely apart as it approached the center of the black hole.
    [Show full text]
  • Cinemática Estelar, Modelos Dinâmicos E Determinaç˜Ao De
    UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL PROGRAMA DE POS´ GRADUA¸CAO~ EM F´ISICA Cinem´atica Estelar, Modelos Din^amicos e Determina¸c~ao de Massas de Buracos Negros Supermassivos Daniel Alf Drehmer Tese realizada sob orienta¸c~aoda Professora Dra. Thaisa Storchi Bergmann e apresen- tada ao Programa de P´os-Gradua¸c~aoem F´ısica do Instituto de F´ısica da UFRGS em preenchimento parcial dos requisitos para a obten¸c~aodo t´ıtulo de Doutor em Ci^encias. Porto Alegre Mar¸co, 2015 Agradecimentos Gostaria de agradecer a todas as pessoas que de alguma forma contribu´ıram para a realiza¸c~ao deste trabalho e em especial agrade¸co: • A` Profa. Dra. Thaisa Storchi-Bergmann pela competente orienta¸c~ao. • Aos professores Dr. Fabr´ıcio Ferrari da Universidade Federal do Rio Grande, Dr. Rogemar Riffel da Universidade Federal de Santa Maria e ao Dr. Michele Cappellari da Universidade de Oxford cujas colabora¸c~oes foram fundamentais para a realiza¸c~ao deste trabalho. • A todos os professores do Departamento de Astronomia do Instituto de F´ısica da Universidade Federal do Rio Grande do Sul que contribu´ıram para minha forma¸c~ao. • Ao CNPq pelo financiamento desse trabalho. • Aos meus pais Ingon e Selia e meus irm~aos Neimar e Carla pelo apoio. Daniel Alf Drehmer Universidade Federal do Rio Grande do Sul Mar¸co2015 i Resumo O foco deste trabalho ´eestudar a influ^encia de buracos negros supermassivos (BNSs) nucleares na din^amica e na cinem´atica estelar da regi~ao central das gal´axias e determinar a massa destes BNSs.
    [Show full text]
  • Virgo the Virgin
    Virgo the Virgin Virgo is one of the constellations of the zodiac, the group tion Virgo itself. There is also the connection here with of 12 constellations that lies on the ecliptic plane defined “The Scales of Justice” and the sign Libra which lies next by the planets orbital orientation around the Sun. Virgo is to Virgo in the Zodiac. The study of astronomy had a one of the original 48 constellations charted by Ptolemy. practical “time keeping” aspect in the cultures of ancient It is the largest constellation of the Zodiac and the sec- history and as the stars of Virgo appeared before sunrise ond - largest constellation after Hydra. Virgo is bordered by late in the northern summer, many cultures linked this the constellations of Bootes, Coma Berenices, Leo, Crater, asterism with crops, harvest and fecundity. Corvus, Hydra, Libra and Serpens Caput. The constella- tion of Virgo is highly populated with galaxies and there Virgo is usually depicted with angel - like wings, with an are several galaxy clusters located within its boundaries, ear of wheat in her left hand, marked by the bright star each of which is home to hundreds or even thousands of Spica, which is Latin for “ear of grain”, and a tall blade of galaxies. The accepted abbreviation when enumerating grass, or a palm frond, in her right hand. Spica will be objects within the constellation is Vir, the genitive form is important for us in navigating Virgo in the modern night Virginis and meteor showers that appear to originate from sky. Spica was most likely the star that helped the Greek Virgo are called Virginids.
    [Show full text]
  • And Ecclesiastical Cosmology
    GSJ: VOLUME 6, ISSUE 3, MARCH 2018 101 GSJ: Volume 6, Issue 3, March 2018, Online: ISSN 2320-9186 www.globalscientificjournal.com DEMOLITION HUBBLE'S LAW, BIG BANG THE BASIS OF "MODERN" AND ECCLESIASTICAL COSMOLOGY Author: Weitter Duckss (Slavko Sedic) Zadar Croatia Pусскй Croatian „If two objects are represented by ball bearings and space-time by the stretching of a rubber sheet, the Doppler effect is caused by the rolling of ball bearings over the rubber sheet in order to achieve a particular motion. A cosmological red shift occurs when ball bearings get stuck on the sheet, which is stretched.“ Wikipedia OK, let's check that on our local group of galaxies (the table from my article „Where did the blue spectral shift inside the universe come from?“) galaxies, local groups Redshift km/s Blueshift km/s Sextans B (4.44 ± 0.23 Mly) 300 ± 0 Sextans A 324 ± 2 NGC 3109 403 ± 1 Tucana Dwarf 130 ± ? Leo I 285 ± 2 NGC 6822 -57 ± 2 Andromeda Galaxy -301 ± 1 Leo II (about 690,000 ly) 79 ± 1 Phoenix Dwarf 60 ± 30 SagDIG -79 ± 1 Aquarius Dwarf -141 ± 2 Wolf–Lundmark–Melotte -122 ± 2 Pisces Dwarf -287 ± 0 Antlia Dwarf 362 ± 0 Leo A 0.000067 (z) Pegasus Dwarf Spheroidal -354 ± 3 IC 10 -348 ± 1 NGC 185 -202 ± 3 Canes Venatici I ~ 31 GSJ© 2018 www.globalscientificjournal.com GSJ: VOLUME 6, ISSUE 3, MARCH 2018 102 Andromeda III -351 ± 9 Andromeda II -188 ± 3 Triangulum Galaxy -179 ± 3 Messier 110 -241 ± 3 NGC 147 (2.53 ± 0.11 Mly) -193 ± 3 Small Magellanic Cloud 0.000527 Large Magellanic Cloud - - M32 -200 ± 6 NGC 205 -241 ± 3 IC 1613 -234 ± 1 Carina Dwarf 230 ± 60 Sextans Dwarf 224 ± 2 Ursa Minor Dwarf (200 ± 30 kly) -247 ± 1 Draco Dwarf -292 ± 21 Cassiopeia Dwarf -307 ± 2 Ursa Major II Dwarf - 116 Leo IV 130 Leo V ( 585 kly) 173 Leo T -60 Bootes II -120 Pegasus Dwarf -183 ± 0 Sculptor Dwarf 110 ± 1 Etc.
    [Show full text]
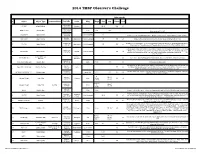
  • 2014 Observers Challenge List
    2014 TMSP Observer's Challenge Atlas page #s # Object Object Type Common Name RA, DEC Const Mag Mag.2 Size Sep. U2000 PSA 18h31m25s 1 IC 1287 Bright Nebula Scutum 20'.0 295 67 -10°47'45" 18h31m25s SAO 161569 Double Star 5.77 9.31 12.3” -10°47'45" Near center of IC 1287 18h33m28s NGC 6649 Open Cluster 8.9m Integrated 5' -10°24'10" Can be seen in 3/4d FOV with above. Brightest star is 13.2m. Approx 50 stars visible in Binos 18h28m 2 NGC 6633 Open Cluster Ophiuchus 4.6m integrated 27' 205 65 Visible in Binos and is about the size of a full Moon, brightest star is 7.6m +06°34' 17h46m18s 2x diameter of a full Moon. Try to view this cluster with your naked eye, binos, and a small scope. 3 IC 4665 Open Cluster Ophiuchus 4.2m Integrated 60' 203 65 +05º 43' Also check out “Tweedle-dee and Tweedle-dum to the east (IC 4756 and NGC 6633) A loose open cluster with a faint concentration of stars in a rich field, contains about 15-20 stars. 19h53m27s Brightest star is 9.8m, 5 stars 9-11m, remainder about 12-13m. This is a challenge obJect to 4 Harvard 20 Open Cluster Sagitta 7.7m integrated 6' 162 64 +18°19'12" improve your observation skills. Can you locate the miniature coathanger close by at 19h 37m 27s +19d? Constellation star Corona 5 Corona Borealis 55 Trace the 7 stars making up this constellation, observe and list the colors of each star asterism Borealis 15H 32' 55” Theta Corona Borealis Double Star 4.2m 6.6m .97” 55 Theta requires about 200x +31° 21' 32” The direction our Sun travels in our galaxy.
    [Show full text]
  • Perseus Perseus
    Lateinischer Name: Deutscher Name: Per Perseus Perseus Atlas (2000.0) Karte Cambridge Star Kulmination um 2, 3 Atlas Mitternacht: Benachbarte 1, 4, Sky Atlas Sternbilder: 5 And Ari Aur Cam Cas 7. November Tau Tri Deklinationsbereich: 30° ... 59° Fläche am Himmel: 615° 2 Mythologie und Geschichte: Akrisios war der König von Argos und hatte eine hübsche Tochter namens Danae. Das Orakel von Delphi prophezeite ihm, sein Enkelsohn werde ihn einst töten. Aus Furcht vor diesem Orakelspruch ließ Akrisios seine Tochter Danae in einen Turm einschließen, damit sie keinen Mann empfangen könne. Akrisios konnte natürlich nicht wissen, dass Zeus selbst sich der liebreizenden Danae nähern wollte. Zeus tat dies auch und nahm dazu die Form eines goldenen Regens an, der durch die Wände, Fugen, Ritzen und Fenster drang. Danae gebar einen Sohn, welcher "Der aus fließendem Gold entstandene" oder auch "Der Goldgeborene" genannt wurde - eben den Perseus. Akrisios blieb dies natürlich nicht lange verborgen und er ließ seine Tochter und sein Enkelkind in einen Kasten einnageln, der dann ins Meer geworfen wurde. Danae und Perseus trieben lange Zeit auf dem Meer, bis sie schließlich an der Küste der steinigen Insel Seriphos strandeten und aus ihrem Gefängnis befreit wurden. Auf dieser Insel herrschte Polydektes, der bald jahrelang um die schöne Danae warb, jedoch vergebens. Entweder um Danae doch noch zur Ehe zu zwingen oder um Perseus aus dem Weg zu schaffen, schickte er den inzwischen zum Jüngling herangewachsenen Sohn der Danae aus, eine tödliche Aufgabe zu erledigen. Er solle das Haupt der Medusa zu holen. Die Medusa war eine der Gorgonen, eine der drei Töchter des Phorkys, die mit Schlangenhaaren ausgestattet waren und einen versteinernden Blick werfen konnten.
    [Show full text]
  • Celebrating the Wonder of the Night Sky
    Celebrating the Wonder of the Night Sky The heavens proclaim the glory of God. The skies display his craftsmanship. Psalm 19:1 NLT Celebrating the Wonder of the Night Sky Light Year Calculation: Simple! [Speed] 300 000 km/s [Time] x 60 s x 60 m x 24 h x 365.25 d [Distance] ≈ 10 000 000 000 000 km ≈ 63 000 AU Celebrating the Wonder of the Night Sky Milkyway Galaxy Hyades Star Cluster = 151 ly Barnard 68 Nebula = 400 ly Pleiades Star Cluster = 444 ly Coalsack Nebula = 600 ly Betelgeuse Star = 643 ly Helix Nebula = 700 ly Helix Nebula = 700 ly Witch Head Nebula = 900 ly Spirograph Nebula = 1 100 ly Orion Nebula = 1 344 ly Dumbbell Nebula = 1 360 ly Dumbbell Nebula = 1 360 ly Flame Nebula = 1 400 ly Flame Nebula = 1 400 ly Veil Nebula = 1 470 ly Horsehead Nebula = 1 500 ly Horsehead Nebula = 1 500 ly Sh2-106 Nebula = 2 000 ly Twin Jet Nebula = 2 100 ly Ring Nebula = 2 300 ly Ring Nebula = 2 300 ly NGC 2264 Nebula = 2 700 ly Cone Nebula = 2 700 ly Eskimo Nebula = 2 870 ly Sh2-71 Nebula = 3 200 ly Cat’s Eye Nebula = 3 300 ly Cat’s Eye Nebula = 3 300 ly IRAS 23166+1655 Nebula = 3 400 ly IRAS 23166+1655 Nebula = 3 400 ly Butterfly Nebula = 3 800 ly Lagoon Nebula = 4 100 ly Rotten Egg Nebula = 4 200 ly Trifid Nebula = 5 200 ly Monkey Head Nebula = 5 200 ly Lobster Nebula = 5 500 ly Pismis 24 Star Cluster = 5 500 ly Omega Nebula = 6 000 ly Crab Nebula = 6 500 ly RS Puppis Variable Star = 6 500 ly Eagle Nebula = 7 000 ly Eagle Nebula ‘Pillars of Creation’ = 7 000 ly SN1006 Supernova = 7 200 ly Red Spider Nebula = 8 000 ly Engraved Hourglass Nebula
    [Show full text]
  • Uncovering the Orbit of the Hercules Dwarf Galaxy
    MNRAS 000,1{15 (2019) Preprint 3 December 2019 Compiled using MNRAS LATEX style file v3.0 Uncovering the Orbit of the Hercules Dwarf Galaxy Alexandra L. Gregory1?, Michelle L. M. Collins1, Denis Erkal1, Erik Tollerud2, Maxime Delorme1, Lewis Hill1, David J. Sand3, Jay Strader4 Beth Willman5, 1Department of Physics, University of Surrey, Guildford, GU2 7XH, Surrey, UK 2Space Telescope Science Institute, 3700 San Martin Dr, Baltimore, MD 21218, USA 3Department of Astronomy/Steward Observatory, 933 North Cherry Avenue, Rm. N204, Tucson, AZ 85721-0065, USA 4Department of Physics and Astronomy, Michigan State University, East Lansing, MI 48824, USA 5National Optical-Infrared Astronomy Research Laboratory, 950 North Cherry Avenue, Tucson, AZ 85719, USA Accepted XXX. Received YYY; in original form ZZZ ABSTRACT We present new chemo{kinematics of the Hercules dwarf galaxy based on Keck II{ DEIMOS spectroscopy. Our 21 confirmed members have a systemic velocity of vHerc = −1 +1:4 −1 46:4 1:3 kms and a velocity dispersion σv;Herc = 4:4−1:2 kms . From the strength of the± Ca II triplet, we obtain a metallicity of [Fe/H]= 2:48 0:19 dex and dispersion +0:18 − ± of σ[Fe=H] = 0:63−0:13 dex. This makes Hercules a particularly metal{poor galaxy, placing it slightly below the standard mass{metallicity relation. Previous photometric and spectroscopic evidence suggests that Hercules is tidally disrupting and may be on a highly radial orbit. From our identified members, we measure no significant velocity gradient. By cross{matching with the second Gaia data release, we determine an ∗ uncertainty{weighted mean proper motion of µα = µα cos(δ) = 0:153 0:074 mas −1 −1 − ± yr , µδ = 0:397 0:063 mas yr .
    [Show full text]