DOCSLIB.ORG

Arguments Validity of Arguments Example the Truth Table

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Arguments Validity of Arguments Example the Truth Table Arguments Definition of a Symbolic Argument Validity of Arguments • An argument is an implication (conditional) • Arguments are either valid or invalid. whose “if” component consists of the • Ways of determining the validity of an Arguments conjunction of several propositions called premises (hypotheses) and whose “then” argument. component is a proposition called the 1. Truth table Determining Validity conclusion. 2. Analysis • Symbolic notation of an argument: 3. Syllogism [P1 P2 P3] → C Chapter 3 – Section 5 In-class Assignment 13 - 1 No in-class assignment problem Validity of an Argument by A Truth Example The Truth Table Table • 2 is an even number. • P1: p • Write each premise and the conclusion in • If 7 is odd then 2 is not • P2: (q → ~p) symbolic form. even. • Enclose each premise and the conclusion that is • If 7 is not odd then 8 is • P3: (~q → r) compound within parentheses. even. • _____________ • Write the conjunction of the several premises. • ________________ • C : r • Enclose the conjunction in braces. • 8 is even. • Write the conditional of the conjunction and the conclusion. Symbolic Argument: [p (q → ~p) (~q → r)] → r • Make a truth table for this symbolic implication. • Only if it is a tautology is the argument valid. The argument is invalid because the implication is not a tautology In-class Assignment 13 - 2 In-class Assignment 13 - 2 In-class Assignment 13 - 3 1 Arguments Validity by Analysis - Reminder Validity by Analysis Syllogisms • A conditional is only false if the “if” • Write the argument in From left to right component is true and the “then” symbolic form. • Identify the premises. component is false. 1. Law of Detachment • Force all premises to be 2. Fallacy of Inverse • A conjunction is true only if all true by using the rules of 3. Disjunction Law 1 logic. 1 components are true. In an argument the 4. Fallacy of Converse • If it is possible for the conjunction is the “if” component. conclusion to be false 5. Chain Rule • Therefore, all premises must be true. then the argument is 6. Law of Contraposition invalid. No in-class assignment problem. In-class assignment 13 - 4 Syllogisms Lead to Valid Recognizing Syllogisms Conclusions 1. If the sun shines then it will not rain. 1. Law of It is raining. • Mary did not go to • A form of p → q Contraposition Therefore, the sun is not shining. school or Tom went p 2. All puppies are cute. Felix is not a puppy. 2. Fallacy of to the store. Therefore, Felix is not cute. converse • Mary went to school. • Use the Law of 3. Sam is wet if he went swimming. Detachment to write the Sam is wet. 3. Law of conclusion. Therefore, Sam went swimming. syllogism (chain rule) 4. If you study hard you get a good grade. If you get a good grade then you can transfer. • Tom went to the Therefore, if you study hard you can transfer. 4. Fallacy of store. inverse In-class Assignment 13 – 5 In-class Assignment 13 - 6 2.
Load more

Recommended publications
  • The Validities of Pep and Some Characteristic Formulas in Modal Logic
    THE VALIDITIES OF PEP AND SOME CHARACTERISTIC FORMULAS IN MODAL LOGIC Hong Zhang, Huacan He School of Computer Science, Northwestern Polytechnical University,Xi'an, Shaanxi 710032, P.R. China Abstract: In this paper, we discuss the relationships between some characteristic formulas in normal modal logic with their frames. We find that the validities of the modal formulas are conditional even though some of them are intuitively valid. Finally, we prove the validities of two formulas of Position- Exchange-Principle (PEP) proposed by papers 1 to 3 by using of modal logic and Kripke's semantics of possible worlds. Key words: Characteristic Formulas, Validity, PEP, Frame 1. INTRODUCTION Reasoning about knowledge and belief is an important issue in the research of multi-agent systems, and reasoning, which is set up from the main ideas of situational calculus, about other agents' states and actions is one of the most important directions in Al^^'^\ Papers [1-3] put forward an axiom scheme in reasoning about others(RAO) in multi-agent systems, and a rule called Position-Exchange-Principle (PEP), which is shown as following, was abstracted . C{(p^y/)^{C(p->Cy/) (Ce{5f',...,5f-}) When the length of C is at least 2, it reflects the mechanism of an agent reasoning about knowledge of others. For example, if C is replaced with Bf B^/, then it should be B':'B]'{(p^y/)-^iBf'B]'(p^Bf'B]'y/) 872 Hong Zhang, Huacan He The axiom schema plays a useful role as that of modus ponens and axiom K when simplifying proof. Though examples were demonstrated as proofs in papers [1-3], from the perspectives both in semantics and in syntax, the rule is not so compellent.
    [Show full text]
  • The Substitutional Analysis of Logical Consequence
    THE SUBSTITUTIONAL ANALYSIS OF LOGICAL CONSEQUENCE Volker Halbach∗ dra version ⋅ please don’t quote ónd June óþÕä Consequentia ‘formalis’ vocatur quae in omnibus terminis valet retenta forma consimili. Vel si vis expresse loqui de vi sermonis, consequentia formalis est cui omnis propositio similis in forma quae formaretur esset bona consequentia [...] Iohannes Buridanus, Tractatus de Consequentiis (Hubien ÕÉßä, .ì, p.óóf) Zf«±§Zh± A substitutional account of logical truth and consequence is developed and defended. Roughly, a substitution instance of a sentence is dened to be the result of uniformly substituting nonlogical expressions in the sentence with expressions of the same grammatical category. In particular atomic formulae can be replaced with any formulae containing. e denition of logical truth is then as follows: A sentence is logically true i all its substitution instances are always satised. Logical consequence is dened analogously. e substitutional denition of validity is put forward as a conceptual analysis of logical validity at least for suciently rich rst-order settings. In Kreisel’s squeezing argument the formal notion of substitutional validity naturally slots in to the place of informal intuitive validity. ∗I am grateful to Beau Mount, Albert Visser, and Timothy Williamson for discussions about the themes of this paper. Õ §Z êZo±í At the origin of logic is the observation that arguments sharing certain forms never have true premisses and a false conclusion. Similarly, all sentences of certain forms are always true. Arguments and sentences of this kind are for- mally valid. From the outset logicians have been concerned with the study and systematization of these arguments, sentences and their forms.
    [Show full text]
  • Propositional Logic (PDF)
    Mathematics for Computer Science Proving Validity 6.042J/18.062J Instead of truth tables, The Logic of can try to prove valid formulas symbolically using Propositions axioms and deduction rules Albert R Meyer February 14, 2014 propositional logic.1 Albert R Meyer February 14, 2014 propositional logic.2 Proving Validity Algebra for Equivalence The text describes a for example, bunch of algebraic rules to the distributive law prove that propositional P AND (Q OR R) ≡ formulas are equivalent (P AND Q) OR (P AND R) Albert R Meyer February 14, 2014 propositional logic.3 Albert R Meyer February 14, 2014 propositional logic.4 1 Algebra for Equivalence Algebra for Equivalence for example, The set of rules for ≡ in DeMorgan’s law the text are complete: ≡ NOT(P AND Q) ≡ if two formulas are , these rules can prove it. NOT(P) OR NOT(Q) Albert R Meyer February 14, 2014 propositional logic.5 Albert R Meyer February 14, 2014 propositional logic.6 A Proof System A Proof System Another approach is to Lukasiewicz’ proof system is a start with some valid particularly elegant example of this idea. formulas (axioms) and deduce more valid formulas using proof rules Albert R Meyer February 14, 2014 propositional logic.7 Albert R Meyer February 14, 2014 propositional logic.8 2 A Proof System Lukasiewicz’ Proof System Lukasiewicz’ proof system is a Axioms: particularly elegant example of 1) (¬P → P) → P this idea. It covers formulas 2) P → (¬P → Q) whose only logical operators are 3) (P → Q) → ((Q → R) → (P → R)) IMPLIES (→) and NOT. The only rule: modus ponens Albert R Meyer February 14, 2014 propositional logic.9 Albert R Meyer February 14, 2014 propositional logic.10 Lukasiewicz’ Proof System Lukasiewicz’ Proof System Prove formulas by starting with Prove formulas by starting with axioms and repeatedly applying axioms and repeatedly applying the inference rule.
    [Show full text]
  • Sets, Propositional Logic, Predicates, and Quantifiers
    COMP 182 Algorithmic Thinking Sets, Propositional Logic, Luay Nakhleh Computer Science Predicates, and Quantifiers Rice University !1 Reading Material ❖ Chapter 1, Sections 1, 4, 5 ❖ Chapter 2, Sections 1, 2 !2 ❖ Mathematics is about statements that are either true or false. ❖ Such statements are called propositions. ❖ We use logic to describe them, and proof techniques to prove whether they are true or false. !3 Propositions ❖ 5>7 ❖ The square root of 2 is irrational. ❖ A graph is bipartite if and only if it doesn’t have a cycle of odd length. ❖ For n>1, the sum of the numbers 1,2,3,…,n is n2. !4 Propositions? ❖ E=mc2 ❖ The sun rises from the East every day. ❖ All species on Earth evolved from a common ancestor. ❖ God does not exist. ❖ Everyone eventually dies. !5 ❖ And some of you might already be wondering: “If I wanted to study mathematics, I would have majored in Math. I came here to study computer science.” !6 ❖ Computer Science is mathematics, but we almost exclusively focus on aspects of mathematics that relate to computation (that can be implemented in software and/or hardware). !7 ❖Logic is the language of computer science and, mathematics is the computer scientist’s most essential toolbox. !8 Examples of “CS-relevant” Math ❖ Algorithm A correctly solves problem P. ❖ Algorithm A has a worst-case running time of O(n3). ❖ Problem P has no solution. ❖ Using comparison between two elements as the basic operation, we cannot sort a list of n elements in less than O(n log n) time. ❖ Problem A is NP-Complete.
    [Show full text]
  • A Validity Framework for the Use and Development of Exported Assessments
    A Validity Framework for the Use and Development of Exported Assessments By María Elena Oliveri, René Lawless, and John W. Young A Validity Framework for the Use and Development of Exported Assessments María Elena Oliveri, René Lawless, and John W. Young1 1 The authors would like to acknowledge Bob Mislevy, Michael Kane, Kadriye Ercikan, and Maurice Hauck for their valuable input and expertise in reviewing various iterations of the framework as well as Priya Kannan, Don Powers, and James Carlson for their input throughout the technical review process. Copyright © 2015 Educational Testing Service. All Rights Reserved. ETS, the ETS logo, GRADUATE RECORD EXAMINATIONS, GRE, LISTENTING. LEARNING. LEADING, TOEIC, and TOEFL are registered trademarks of Educational Testing Service (ETS). EXADEP and EXAMEN DE ADMISIÓN A ESTUDIOS DE POSGRADO are trademarks of ETS. 1 Abstract In this document, we present a framework that outlines the key considerations relevant to the fair development and use of exported assessments. Exported assessments are developed in one country and are used in countries with a population that differs from the one for which the assessment was developed. Examples of these assessments include the Graduate Record Examinations® (GRE®) and el Examen de Admisión a Estudios de Posgrado™ (EXADEP™), among others. Exported assessments can be used to make inferences about performance in the exporting country or in the receiving country. To illustrate, the GRE can be administered in India and be used to predict success at a graduate school in the United States, or similarly it can be administered in India to predict success in graduate school at a graduate school in India.
    [Show full text]
  • From Fuzzy Sets to Crisp Truth Tables1 Charles C. Ragin
    From Fuzzy Sets to Crisp Truth Tables1 Charles C. Ragin Department of Sociology University of Arizona Tucson, AZ 85721 USA [email protected] Version: April 2005 1. Overview One limitation of the truth table approach is that it is designed for causal conditions are simple presence/absence dichotomies (i.e., Boolean or "crisp" sets). Many of the causal conditions that interest social scientists, however, vary by level or degree. For example, while it is clear that some countries are democracies and some are not, there are many in-between cases. These countries are not fully in the set of democracies, nor are they fully excluded from this set. Fortunately, there is a well-developed mathematical system for addressing partial membership in sets, fuzzy-set theory. Section 2 of this paper provides a brief introduction to the fuzzy-set approach, building on Ragin (2000). Fuzzy sets are especially powerful because they allow researchers to calibrate partial membership in sets using values in the interval between 0 (nonmembership) and 1 (full membership) without abandoning core set theoretic principles, for example, the subset relation. Ragin (2000) demonstrates that the subset relation is central to the analysis of multiple conjunctural causation, where several different combinations of conditions are sufficient for the same outcome. While fuzzy sets solve the problem of trying to force-fit cases into one of two categories (membership versus nonmembership in a set), they are not well suited for conventional truth table analysis. With fuzzy sets, there is no simple way to sort cases according to the combinations of causal conditions they display because each case's array of membership scores may be unique.
    [Show full text]
  • 12 Propositional Logic
    CHAPTER 12 ✦ ✦ ✦ ✦ Propositional Logic In this chapter, we introduce propositional logic, an algebra whose original purpose, dating back to Aristotle, was to model reasoning. In more recent times, this algebra, like many algebras, has proved useful as a design tool. For example, Chapter 13 shows how propositional logic can be used in computer circuit design. A third use of logic is as a data model for programming languages and systems, such as the language Prolog. Many systems for reasoning by computer, including theorem provers, program verifiers, and applications in the field of artificial intelligence, have been implemented in logic-based programming languages. These languages generally use “predicate logic,” a more powerful form of logic that extends the capabilities of propositional logic. We shall meet predicate logic in Chapter 14. ✦ ✦ ✦ ✦ 12.1 What This Chapter Is About Section 12.2 gives an intuitive explanation of what propositional logic is, and why it is useful. The next section, 12,3, introduces an algebra for logical expressions with Boolean-valued operands and with logical operators such as AND, OR, and NOT that Boolean algebra operate on Boolean (true/false) values. This algebra is often called Boolean algebra after George Boole, the logician who first framed logic as an algebra. We then learn the following ideas. ✦ Truth tables are a useful way to represent the meaning of an expression in logic (Section 12.4). ✦ We can convert a truth table to a logical expression for the same logical function (Section 12.5). ✦ The Karnaugh map is a useful tabular technique for simplifying logical expres- sions (Section 12.6).
    [Show full text]
  • Lecture 1: Propositional Logic
    Lecture 1: Propositional Logic Syntax Semantics Truth tables Implications and Equivalences Valid and Invalid arguments Normal forms Davis-Putnam Algorithm 1 Atomic propositions and logical connectives An atomic proposition is a statement or assertion that must be true or false. Examples of atomic propositions are: “5 is a prime” and “program terminates”. Propositional formulas are constructed from atomic propositions by using logical connectives. Connectives false true not and or conditional (implies) biconditional (equivalent) A typical propositional formula is The truth value of a propositional formula can be calculated from the truth values of the atomic propositions it contains. 2 Well-formed propositional formulas The well-formed formulas of propositional logic are obtained by using the construction rules below: An atomic proposition is a well-formed formula. If is a well-formed formula, then so is . If and are well-formed formulas, then so are , , , and . If is a well-formed formula, then so is . Alternatively, can use Backus-Naur Form (BNF) : formula ::= Atomic Proposition formula formula formula formula formula formula formula formula formula formula 3 Truth functions The truth of a propositional formula is a function of the truth values of the atomic propositions it contains. A truth assignment is a mapping that associates a truth value with each of the atomic propositions . Let be a truth assignment for . If we identify with false and with true, we can easily determine the truth value of under . The other logical connectives can be handled in a similar manner. Truth functions are sometimes called Boolean functions. 4 Truth tables for basic logical connectives A truth table shows whether a propositional formula is true or false for each possible truth assignment.
    [Show full text]
  • Propositional Logic, Truth Tables, and Predicate Logic (Rosen, Sections 1.1, 1.2, 1.3) TOPICS
    Propositional Logic, Truth Tables, and Predicate Logic (Rosen, Sections 1.1, 1.2, 1.3) TOPICS • Propositional Logic • Logical Operations • Equivalences • Predicate Logic Logic? What is logic? Logic is a truth-preserving system of inference Truth-preserving: System: a set of If the initial mechanistic statements are transformations, based true, the inferred on syntax alone statements will be true Inference: the process of deriving (inferring) new statements from old statements Proposi0onal Logic n A proposion is a statement that is either true or false n Examples: n This class is CS122 (true) n Today is Sunday (false) n It is currently raining in Singapore (???) n Every proposi0on is true or false, but its truth value (true or false) may be unknown Proposi0onal Logic (II) n A proposi0onal statement is one of: n A simple proposi0on n denoted by a capital leJer, e.g. ‘A’. n A negaon of a proposi0onal statement n e.g. ¬A : “not A” n Two proposi0onal statements joined by a connecve n e.g. A ∧ B : “A and B” n e.g. A ∨ B : “A or B” n If a connec0ve joins complex statements, parenthesis are added n e.g. A ∧ (B∨C) Truth Tables n The truth value of a compound proposi0onal statement is determined by its truth table n Truth tables define the truth value of a connec0ve for every possible truth value of its terms Logical negaon n Negaon of proposi0on A is ¬A n A: It is snowing. n ¬A: It is not snowing n A: Newton knew Einstein. n ¬A: Newton did not know Einstein.
    [Show full text]
  • Valid Arguments
    CHAPTER 3 Logic Copyright © 2015, 2011, 2007 Pearson Education, Inc. Section 3.7, Slide 1 3.7 Arguments and Truth Tables Copyright © 2015, 2011, 2007 Pearson Education, Inc. Section 3.7, Slide 2 Objectives 1. Use truth tables to determine validity. 2. Recognize and use forms of valid and invalid arguments. Copyright © 2015, 2011, 2007 Pearson Education, Inc. Section 3.7, Slide 3 Arguments An Argument consists of two parts: Premises: the given statements. Conclusion: the result determined by the truth of the premises. Valid Argument: The conclusion is true whenever the premises are assumed to be true. Invalid Argument: Also called a fallacy Truth tables can be used to test validity. Copyright © 2015, 2011, 2007 Pearson Education, Inc. Section 3.7, Slide 4 Testing the Validity of an Argument with a Truth Table Copyright © 2015, 2011, 2007 Pearson Education, Inc. Section 3.7, Slide 5 Example: Did the Pickiest Logician in the Galaxy Foul Up? In Star Trek, the spaceship Enterprise is hit by an ion storm, causing the power to go out. Captain Cook wonders if Mr. Scott is aware of the problem. Mr. Spock replies, “If Mr. Scott is still with us, the power should be on momentarily.” Moments later the ship’s power comes back on. Argument: If Mr. Scott is still with us, then the power will come on. The power comes on. Therefore, Mr. Scott is still with us. Determine whether the argument is valid or invalid. Copyright © 2015, 2011, 2007 Pearson Education, Inc. Section 3.7, Slide 6 Example continued Solution Step 1: p: Mr.
    [Show full text]
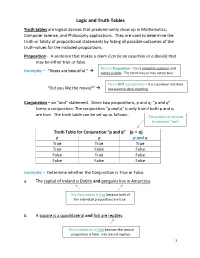
  • Logic and Truth Tables Truth Tables Are Logical Devices That Predominantly Show up in Mathematics, Computer Science, and Philosophy Applications
    Logic and Truth Tables Truth tables are logical devices that predominantly show up in Mathematics, Computer Science, and Philosophy applications. They are used to determine the truth or falsity of propositional statements by listing all possible outcomes of the truth-values for the included propositions. Proposition - A sentence that makes a claim (can be an assertion or a denial) that may be either true or false. This is a Proposition – It is a complete sentence and Examples – “Roses are beautiful.” makes a claim. The claim may or may not be true. This is NOT a proposition – It is a question and does “Did you like the movie?” not assert or deny anything. Conjunction – an “and” statement. Given two propositions, p and q, “p and q” forms a conjunction. The conjunction “p and q” is only true if both p and q are true. The truth table can be set up as follows… This symbol can be used to represent “and”. Truth Table for Conjunction “p and q” (p ˄ q) p q p and q True True True True False False False True False False False False Examples – Determine whether the Conjunction is True or False. a. The capital of Ireland is Dublin and penguins live in Antarctica. This Conjunction is True because both of the individual propositions are true. b. A square is a quadrilateral and fish are reptiles. This Conjunction is False because the second proposition is false. Fish are not reptiles. 1 Disjunction – an “or” statement. Given two propositions, p and q, “p or q” forms a disjunction.
    [Show full text]
  • Validity and Soundness
    1.4 Validity and Soundness A deductive argument proves its conclusion ONLY if it is both valid and sound. Validity: An argument is valid when, IF all of it’s premises were true, then the conclusion would also HAVE to be true. In other words, a “valid” argument is one where the conclusion necessarily follows from the premises. It is IMPOSSIBLE for the conclusion to be false if the premises are true. Here’s an example of a valid argument: 1. All philosophy courses are courses that are super exciting. 2. All logic courses are philosophy courses. 3. Therefore, all logic courses are courses that are super exciting. Note #1: IF (1) and (2) WERE true, then (3) would also HAVE to be true. Note #2: Validity says nothing about whether or not any of the premises ARE true. It only says that IF they are true, then the conclusion must follow. So, validity is more about the FORM of an argument, rather than the TRUTH of an argument. So, an argument is valid if it has the proper form. An argument can have the right form, but be totally false, however. For example: 1. Daffy Duck is a duck. 2. All ducks are mammals. 3. Therefore, Daffy Duck is a mammal. The argument just given is valid. But, premise 2 as well as the conclusion are both false. Notice however that, IF the premises WERE true, then the conclusion would also have to be true. This is all that is required for validity. A valid argument need not have true premises or a true conclusion.
    [Show full text]