Risk Aversion in Game Shows
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

American Idol S3 Judge Audition Venue Announcement 2019
Aug. 5, 2019 TELEVISION’S ICONIC STAR-MAKER ‘AMERICAN IDOL’ HITS THE RIGHT NOTES LUKE BRYAN, KATY PERRY AND LIONEL RICHIE TO RETURN FOR NEW SEASON ON ABC Twenty-two City Cross-Country Audition Tour Kicked Off on Tuesday, JuLy 23, in BrookLyn, New York Bobby Bones to Return as In-House Mentor In its second season on ABC, “American Idol” dominated Sunday nights and claimed the position as Sunday’s No. 1 most social show. In doing so, the reality competition series also proved that untapped talent from coast to coast is still waiting to be discovered. As previously announced, the star-maker will continue to help young singers realize their dreams with an all-new season premiering spring 2020. Returning to help find the next singing sensation are music industry legends and all-star judges Luke Bryan, Katy Perry and Lionel Richie. Multimedia personality Bobby Bones will return as in-house mentor. The all-new nationwide search for the next superstar kicked off with open call auditions in Brooklyn, New York, and will advance on to 21 additional cities across the country. In addition to auditioning in person, hopefuls can also submit audition videos online or show off their talent via Instagram, Facebook or Twitter using the hashtag #TheNextIdol. “‘American Idol’ is the original music competition series,” said Karey Burke, president, ABC Entertainment. “It was the first of its kind to take everyday singers and catapult them into superstardom, launching the careers of so many amazing artists. We couldn’t be more excited for Katy, Luke, Lionel and Bobby to continue in their roles as ‘American Idol’ searches for the next great music star, with more live episodes and exciting, new creative elements coming this season.” “We are delighted to have our judges Katy, Luke and Lionel as well as in-house mentor Bobby back on ‘American Idol,’” said executive producer and showrunner Trish Kinane. -

PRESS RELEASE Endless Games Deals New Card Sharks Game
PRESS RELEASE For Immediate Release Media Contact: Greg Walsh, Walsh Public Relations 305 Knowlton Street, Bridgeport, CT 06608 [email protected]; 203-292-6280 Endless Games Deals New Card Sharks Game New York, NY - (January 29, 2020) – Endless Games gets “deal” to expand its licensed TV Game Show category with a home version of the current hit ABC-TV Game Show, Card Sharks, hosted by funnyman Joel McHale. Debuting at The 2020 American International Toy Fair in New York, Endless Games (Javits Center Booth 165) will debut the Official Card Sharks TV Game Show Game (MSRP $24.99 for 3 or more players ages 14+) which brings all of the fun of the show into your home for friends and family to play together. Card Sharks is the game where one turn of a playing card can make you a winner or a loser! Answer tough guess-timate questions, while your opponent has to choose if you guessed too high or too low. The winner has a chance to predict their hand of cards one at a time. In the Endless Games home version of Card Sharks, individuals can play as solo contestants or a large group can organize for team play. Card Sharks is latest in Endless Games’ extremely successful line of game show adaptations, which already includes Jeopardy and Wheel of Fortune Card Games and Junior Card Games, as well as Password board game. About Endless Games: Founded in 1996 by industry veterans Mike Gasser, Kevin McNulty and game inventor Brian Turtle, Endless Games specializes in games that offer classic entertainment and hours of fun at affordable prices. -

Epic Television Events Clue
Nov. 18, 2019 CATEGORY: EPIC TELEVISION EVENTS CLUE: THE THREE HIGHEST MONEY WINNERS IN ‘JEOPARDY!’ HISTORY COMING TO ABC IN A PRIME-TIME COMPETITION HOSTED BY ALEX TREBEK CORRECT RESPONSE: WHO ARE KEN JENNINGS, BRAD RUTTER AND JAMES HOLZHAUER? The Multiple Consecutive Night Event, ‘JEOPARDY! The Greatest of All Time,’ Begins Tuesday, Jan. 7, on ABC Photo credit: Jeopardy Productions Inc.* On the heels of the iconic Tournament of Champions, “JEOPARDY!” is coming to ABC in a multiple consecutive night event with “JEOPARDY! The Greatest of All Time,” premiering TUESDAY, JAN. 7 (8:00-9:00 p.m. EST), on ABC. Hosted by Alex Trebek, “JEOPARDY! The Greatest of All Time” is produced by Sony Pictures Television. Harry Friedman will executive produce. This epic television event brings together the three highest money winners in the long-running game show’s history: Ken Jennings, Brad Rutter and James Holzhauer. The “JEOPARDY!” fan favorites will compete in a series of matches; the first to win three receives $1 million and the title of “JEOPARDY! The Greatest of All Time.” The two runners up will each receive $250,000. “Based on their previous performances, these three are already the ‘greatest,’ but you can’t help wondering: who is the best of the best?” Trebek said. “I am always so blown away by the incredibly talented and legendary Alex Trebek who has entertained, rallied and championed the masses for generations—and the world class ‘JEOPARDY!’ team who truly are ‘the greatest of all time,’” Said Karey Burke, President, ABC Entertainment. “This timeless and extraordinary format is the gift that keeps on giving and winning the hearts of America every week. -

Before the FEDERAL COMMUNICATIONS COMMISSION Washington, D.C
REDACTED - FOR PUBLIC INSPECTION Before the FEDERAL COMMUNICATIONS COMMISSION Washington, D.C. ) In the Matter of ) ) Game Show Network, LLC, ) ) Complainant, ) File No. CSR-8529-P ) v. ) ) Cablevision Systems Corporation, ) ) Defendant. ) EXPERT REPORT OF MICHAEL EGAN REDACTED - FOR PUBLIC INSPECTION TABLE OF CONTENTS Page I. INTRODUCTION ...............................................................................................................1 II. QUALIFICATIONS ............................................................................................................1 III. METHODOLOGY ..............................................................................................................4 IV. SUMMARY OF CONCLUSIONS......................................................................................5 V. THE PROGRAMMING ON GSN IS NOT AND WAS NOT SIMILAR TO THAT ON WE tv AND WEDDING CENTRAL .........................................................................11 A. GSN Is Not Similar In Genre To WE tv................................................................11 1. WE tv devoted 93% of its broadcast hours to its top five genres of Reality, Comedy, Drama, Movie, and News while GSN aired content of those genres in less than 3% of its airtime. WE tv offers programming in 10 different genres while virtually all of GSN’s programming is found in just two genres. .................................................11 2. The 2012 public {{** **}} statements of GSN’s senior executives affirm that it has been a Game Show network -

The Paley Center for Media Announces New Selections to Its Paley Front Row Series
THE PALEY CENTER FOR MEDIA ANNOUNCES NEW SELECTIONS TO ITS PALEY FRONT ROW SERIES Selections Include: Apple’s Central Park: A Conversation with the Stars and Creative Team, MSNBC’s Know Your Value: On-Air & At Home - A Conversation About Reporting the Story While Living Through It, and ABC’s Summer Fun & Game Show Hosts @ Home Participants Include: Anthony Anderson, Alec Baldwin, Kristen Bell, Loren Bouchard, Mika Brzezinski, Daveed Diggs, Josh Gad, Kathryn Hahn, Steve Harvey, Sheinelle Jones, Alicia Mendez, Leslie Odom, Jr., Rob Riggle, Stephanie Ruhle, Sanjay Shah, Nora Smith, Michael Strahan, Halsted Sullivan, Joe Tessitore, Katy Tur, and Yasmin Vossoughian All Programs Will Be Available on the Paley Center’s YouTube Channel Paley Front Row Series is Part of Paley@Home Presented by Citi New York, NY, May 26, 2020 – The Paley Center for Media today announced new selections to its Paley Front Row series: Apple’s Central Park: A Conversation with the Stars and Creative Team, MSNBC’s Know Your Value: On-Air & At Home - A Conversation About Reporting the Story While Living Through It, and ABC’s Summer Fun & Game Show Hosts @ Home. All three programs will be available for view on the Paley Center’s YouTube channel. Paley Front Row is part of Paley@Home Presented by Citi, a new way to enjoy the behind-the-scenes stories of today’s top shows from the comfort of home. “We’re thrilled to announce the next three highly-anticipated selections in our Paley@Home Presented by Citi series,” said Maureen J. Reidy, the Paley Center’s President & CEO. -

Double Dare (CBS Game Show)
Double Dare (CBS game show) A âœDouble Dare Live!â tour will launch in October, bringing a live version of the show to cities across the country. Former host Marc Summers will join the tour, and audience members may get chosen to to answer trivia questions, completely physical stunts and run the showâ™s obstacle course. ANAHEIM, CA â“ JUNE 22: Youtube personality Josh Killacky experiences the Double Dare obstacle course at Nickelodeonâ™s booth at 2018 VidCon at Anaheim Convention Center on June 22, 2018 in Anaheim, California. (Photo by Charley Gallay/Getty Images for Nickelodeon). The tour will be at the Benedum Center in d Double Dare is an American television game show, produced by Mark Goodsonâ”Bill Todman Productions, that ran from 1976 to 1977 on CBS. Alex Trebek was the host, with Johnny Olson and later Gene Wood announcing. The show was created by Jay Wolpert. Two contestants, each in separate isolation booths, attempted to correctly identify a person, place or thing based on one-sentence clues that were given to them, one at a time, on an electronic gameboard. The correct response was shown to the home audience This short lived game show ran on CBS from December 13, 1976 through April 29, 1977 with host Alex Trebek and announcer Johnny Olson. The following year after cancellation, Card Sharks debuted on NBC with the exact same music soundtrack. Description Edit. This short lived game show ran on CBS from December 13, 1976 through April 29, 1977 with host Alex Trebek and announcer Johnny Olson. -
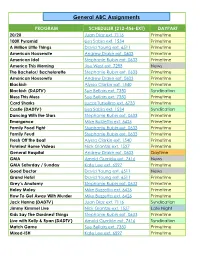
Fall Generalassignmentsgrid
General ABC Assignments PROGRAM SCHEDULER (212-456-EXT) DAYPART 20/20 Juan Diaz ext. 7116 Primetime 100K Pyramid Lisa Sabia ext. 1534 Primetime A Million Little Things David Young ext. 6511 Primetime American Housewife Andrew Drake ext. 0603 Primetime American Idol Stephanie Rubin ext. 0633 Primetime America This Morning Joe West ext. 7288 News The Bachelor/ Bachelorette Stephanie Rubin ext. 0633 Primetime American Housewife Andrew Drake ext. 0603 Primetime Blackish Alyssa Clarkin ext. 1540 Primetime Blackish (DADTV) Sue Bellairs ext. 7350 Syndication Bless This Mess Sue Bellairs ext. 7350 Primetime Card Sharks Lucas Tursellino ext. 6733 Primetime Castle (DADTV) Lisa Sabia ext. 1534 Syndication Dancing With the Stars Stephanie Rubin ext. 0633 Primetime Emergence Mike Buzzetta ext. 6426 Primetime Family Food Fight Stephanie Rubin ext. 0633 Primetime Family Feud Stephanie Rubin ext. 0633 Primetime Fresh Off the Boat Alyssa Clarkin ext. 1540 Primetime Funniest Home Videos Nick Glantzis ext. 1527 Primetime General Hospital Andrew Drake ext. 0603 Daytime GMA Arnold Gumble ext. 7416 News GMA Saturday / Sunday Kate Lee ext. 6597 Primetime Good Doctor David Young ext. 6511 News Grand Hotel David Young ext. 6511 Primetime Grey’s Anatomy Stephanie Rubin ext. 0633 Primetime Holey Moley Mike Buzzetta ext. 6426 Primetime How To Get Away With Murder Mike Buzzetta ext. 6426 Primetime Jack Hanna (DADTV) Juan Diaz ext. 7116 Syndication Jimmy Kimmel Live Nick Glantzis ext. 1527 Late Night Kids Say The Dardnest Things Stephanie Rubin ext. 0633 Primetime Live with Kelly & Ryan (DADTV) Arnold Gumble ext. 7416 Syndication Match Game Sue Bellairs ext. 7350 Primetime Mixed-ISH Kate Lee ext. -

Highs and Lows
August 3 - 9, 2019 Highs and lows Zendaya stars in “Euphoria” AUTO HOME FLOOD LIFE WORK 101 E. Clinton St., Roseboro, N.C. 910-525-5222 [email protected] We ought to weigh well, what we can only once decide. SEE WHAT YOUR NEIGHBORS Complete Funeral Service including: Traditional Funerals, Cremation Pre-Need-Pre-Planning Independently Owned & Operated ARE TALKING ABOUT! Since 1920’s FURNITURE - APPLIANCES - FLOOR COVERING ELECTRONICS - OUTDOOR POWER EQUIPMENT 910-592-7077 Butler Funeral Home 401 W. Roseboro Street 2 locations to Hwy. 24 Windwood Dr. Roseboro, NC better serve you Stedman, NC www.clintonappliance.com 910-525-5138 910-223-7400 910-525-4337 (fax) 910-307-0353(fax) Page 2 — Saturday, August 3, 2019 — Sampson Independent On the Cover Generation Z(endaya): Freshman season of ‘Euphoria’ wraps up on HBO By Breanna Henry TV Media ue Bennett is a drug addict. RDespite having been recently released from a rehab center, she is not recovering, and does not in- tend to remain clean. She routine- ly meets strangers online for “hook-ups,” browses sketchy websites, and lies about her age. Rue is only 17-years-old, and luckily for her parents, she is a fic- tional character from the premium cable show “Euphoria,” played by Disney Channel graduate Zendaya (“Spider-Man: Far From Home,” 2019). If you haven’t been keep- ing up with “Euphoria” so far, you can stream previous episodes on HBO Go, and the Season 1 finale (titled “And Salt the Earth Behind You”) airs Sunday, Aug. 4, on HBO. The fantastic cast of fresh young actors “Euphoria” revolves around includes Jacob Elordi (“The Kissing Booth,” 2018) as angry, confused jock Nate; Algee Smith (“The Hate U Give,” 2018) as struggling college athlete Chris; Barbie Ferreira (“Divorce”) as insecure, sexually curious Kat; Sydney Sweeney (“Sharp Ob- jects”) as Cassie, who can’t seem to escape her past; and the show’s breakout star, trans runway model Hunter Schafer in her first role as Jules, a transgender teen girl look- ing to find the place she belongs. -

The Mathematics of Game Shows
The Mathematics of Game Shows Frank Thorne May 1, 2018 These are the course notes for a class on The Mathematics of Game Shows which I taught at the University of South Carolina (through their Honors College) in Fall 2016, and again in Spring 2018. They are in the middle of revisions, being made as I teach the class a second time. Click here for the course website and syllabus: Link: The Mathematics of Game Shows { Course Website and Syllabus I welcome feedback from anyone who reads this (please e-mail me at thorne[at]math. sc.edu). The notes contain clickable internet links to clips from various game shows, hosted on the video sharing site Youtube (www.youtube.com). These materials are (presumably) all copyrighted, and as such they are subject to deletion. I have no control over this. Sorry! If you encounter a dead link I recommend searching Youtube for similar videos. The Price Is Right videos in particular appear to be ubiquitous. I would like to thank Bill Butterworth, Paul Dreyer, and all of my students for helpful feedback. I hope you enjoy reading these notes as much as I enjoyed writing them! Contents 1 Introduction 4 2 Probability 7 2.1 Sample Spaces and Events . .7 2.2 The Addition and Multiplication Rules . 14 2.3 Permutations and Factorials . 23 2.4 Exercises . 28 3 Expectation 33 3.1 Definitions and Examples . 33 3.2 Linearity of expectation . 44 3.3 Some classical examples . 47 1 3.4 Exercises . 52 3.5 Appendix: The Expected Value of Let 'em Roll . -
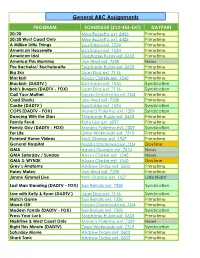
General ABC Assignments
General ABC Assignments PROGRAM SCHEDULER (212-456-EXT) DAYPART 20/20 Mike Buzzetta ext. 6426 Primetime 20/20 West Coast Only Mike Buzzetta ext. 6426 Primetime A Million Little Things Lisa Sabia ext. 1534 Primetime American Housewife Lisa Sabia ext. 1534 Primetime American Idol Stephanie Rubin ext. 0633 Primetime America This Morning Joe West ext. 7288 News The Bachelor/ Bachelorette Stephanie Rubin ext. 0633 Primetime Big Sky Juan Diaz ext. 7116 Primetime Blackish Alyssa Clarkin ext. 1540 Primetime Blackish (DADTV ) Lisa Sabia ext. 1534 Syndication Bob's Burgers (DADTV - FOX) Juan Diaz ext. 7116 Syndication Call Your Mother Magda Chrzanowska ext. 7334 Primetime Card Sharks Joe West ext. 7288 Primetime Castle (DADTV ) Lisa Sabia ext. 1534 Syndication COPS (DADTV - FOX) Monica Palermo ext. 7309 Syndication Dancing With the Stars Stephanie Rubin ext. 0633 Primetime Family Feud Kate Lee ext. 6597 Primetime Family Guy (DADTV - FOX) Monica Palermo ext. 7309 Syndication For Life Drew Wickrowski ext. 7319 Primetime Funniest Home Videos Nick Glantzis ext. 1527 Primetime General Hospital Magda Chrzanowska ext. 7334 Daytime GMA Arnold Gumble ext. 7416 News GMA Saturday / Sunday Alyssa Clarkin ext. 1540 News GMA 3: WYN2K Alyssa Clarkin ext. 1540 Daytime Grey’s Anatomy Andrew Drake ext. 0603 Primetime Holey Moley Joe West ext. 7288 Primetime Jimmy Kimmel Live Nick Glantzis ext. 1527 Late Night Last Man Standing (DADTV - FOX) Sue Bellairs ext. 7350 Syndication Live with Kelly & Ryan (DADTV ) Juan Diaz ext. 7116 Syndication Match Game Sue Bellairs ext. 7350 Primetime Mixed-ISH Magda Chrzanowska ext. 7334 Primetime Modern Family (DADTV - FOX) Sue Bellairs ext. 7350 Syndication Press Your Luck Stephanie Rubin ext. -

Hourly Bonus: Game Shows Game Shows Have Been Around in the US Since the Early Days of Radio
Second Place Stars presents… Hourly Bonus: Game Shows Game shows have been around in the US since the early days of radio. They rose to popularity in the 1950s as television was introduced in many homes and have since survived scandals and fluctuating ratings to remain a mainstay on the airwaves, offering to viewers a unique vicarious emotional experience. Try your hand at these game show questions and challenges: I. Identify the show from the still frame. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 20. II. Answer the following general questions. 21. Which game show was originally to be called What’s the Question? 22. Which host of a 2000s game show refused to shake hands with contestants, o!ering to bump "sts instead? 23. Which game show appears in the opening scene a 2002 movie about a legendary impostor? 24. A short-lived “Super” edition of a show hosted by whom was the "rst to o!er a eight-"gure prize (which nobody won)? 25. The host of which FOX game show had a name that sounds identical to a lead actor of The Other Guys? 26. Which show featured a honeycomb-shaped board "lled with letters? 27. In which 1996 movie did the title character’s family watch a "ctional game show in which contestants were covered in a sticky substance and attempted to grab cash falling from the ceiling? 28. Which show has a wheel labeled with amounts of money in 5-cent increments? 29. -
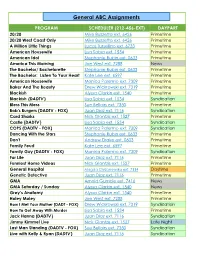
General Assignments Grid Spring 2020
General ABC Assignments PROGRAM SCHEDULER (212-456-EXT) DAYPART 20/20 Mike Buzzetta ext. 6426 Primetime 20/20 West Coast Only Mike Buzzetta ext. 6426 Primetime A Million Little Things Lucas Tursellino ext. 6733 Primetime American Housewife Lisa Sabia ext. 1534 Primetime American Idol Stephanie Rubin ext. 0633 Primetime America This Morning Joe West ext. 7288 News The Bachelor/ Bachelorette Stephanie Rubin ext. 0633 Primetime The Bachelor: Listen To Your Heart Kate Lee ext. 6597 Primetime American Housewife Monica Palermo ext. 7309 Primetime Baker And The Beauty Drew Wickrowski ext. 7319 Primetime Blackish Alyssa Clarkin ext. 1540 Primetime Blackish (DADTV) Lisa Sabia ext. 1534 Syndication Bless This Mess Sue Bellairs ext. 7350 Primetime Bob's Burgers (DADTV - FOX) Juan Diaz ext. 7116 Syndication Card Sharks Nick Glantzis ext. 1527 Primetime Castle (DADTV) Lisa Sabia ext. 1534 Syndication COPS (DADTV - FOX) Monica Palermo ext. 7309 Syndication Dancing With the Stars Stephanie Rubin ext. 0633 Primetime Don't Andrew Drake ext. 0603 Primetime Family Feud Kate Lee ext. 6597 Primetime Family Guy (DADTV - FOX) Monica Palermo ext. 7309 Syndication For Life Juan Diaz ext. 7116 Primetime Funniest Home Videos Nick Glantzis ext. 1527 Primetime General Hospital Magda Chrzanowska ext. 7334 Daytime Genetic Detective Juan Diaz ext. 7116 Primetime GMA Arnold Gumble ext. 7416 News GMA Saturday / Sunday Alyssa Clarkin ext. 1540 News Grey’s Anatomy Alyssa Clarkin ext. 1540 Primetime Holey Moley Joe West ext. 7288 Primetime How I Met Your Mother (DADT - FOX) Drew Wickrowski ext. 7319 Syndication How To Get Away With Murder Lisa Sabia ext. 1534 Primetime Jack Hanna (DADTV) Juan Diaz ext.