Stability of Elastic Grid Shells
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

2021 European Indoor Championships Statistics – Men PV
2021 European Indoor Championships Statistics – Men PV by KKenNakamura Summary Page: All time performance list at the European Indoor Championships Performance Performer Height Name Nat Pos Venue Year 1 1 6.04 Renaud Lavillenie FRA 1 Praha 20 15 2 6.03 Ren aud Lavillenie 1 Paris 2011 3 6.01 Renaud Lavillenie 1 Göteborg 2013 4 2 5.90 Pyotr Bochkaryov RUS 1 Paris 1994 4 2 5.90 Igor Pavlov RUS 1 Madrid 2005 4 2 5.90 Pawel Wojciechowski POL 1 Glasgow 2019 Margin of Victory Differe nce Height Name Nat Venue Year Max 27cm 6.03m Renaud Lavillenie FRA Paris 2011 25cm 6.01m Renaud Lavillenie FRA Göteborg 2013 Min 0cm 5.40 Wolfgang Nordwig GDR Grenoble 1972 5.60 Konstantin Volkov URS Sindelfingen 1980 5.60 Vladimir Polyakov URS Budapest 1983 5.70 Sergey Bubka URS Piraeus 1985 5.70 Atanas Tarev BUL Madrid 1986 5.85 Thierry Vigneron FRA Lievin 1987 5.75 Grigoriy Yegorov URS Den Haag 1989 5.80 Tim Lobinger GER Valencia 1998 5.75 Tim Lobinger GER Wien 2002 5.85 Piotr Lisek POL Beograd 2017 Best Marks for Places in the European Indoor Championships Po s Height Name Nat Venue Year 1 6.04 Renaud Lavillenie FR A Praha 20 15 6.03 Renaud Lavillenie FRA Paris 2011 2 5.85 Ferenc Salbert FRA Lieven 1987 Aleksandr Gripich RUS Praha 2015 Konstadinos Filippidis GRE Beograd 2017 Pio tr Lisek POL Glasgow 2019 3 5.85 Piotr Lisek POL Praha 2015 Pawel Wojciechowski POL Beograd 2017 Highest vault in each round at European Indoor Championships Round Heigh t Name Nat Position Venue Year Final 6.03 Renaud Lavillenie FRA 1 Paris 2011 First round 5.70 Artem Kuptsov RUS 1qA Madrid 2005 Lavillenie, Gripich, Lisek et.al. -

Men's Pole Vault International 02.09.2015
Men's Pole Vault International 02.09.2015 Start list Pole Vault Time: 18:00 Records Order Athlete Nat PB SB WR 6.16Renaud LAVILLENIE FRA Donetsk 15.02.14 1 Marquis RICHARDS SUI 5.55 5.30 AR 6.16Renaud LAVILLENIE FRA Donetsk 15.02.14 2 Mitch GREELEY USA 5.56 5.50 NR 5.71Felix BÖHNI SUI Bern 11.06.83 3 Carlo PAECH GER 5.80 5.80 WJR 5.80Maxim TARASOV URS Bryansk 14.07.89 4 Tobias SCHERBARTH GER 5.73 5.70 WJR 5.80 Raphael HOLZDEPPE GER Biberach 28.06.08 5 Konstantinos FILIPPIDIS GRE 5.91 5.91 MR 5.95Igor TRANDENKOV RUS 14.08.96 DLR 6.05Renaud LAVILLENIE FRA Eugene 30.05.15 6 Piotr LISEK POL 5.82 5.82 SB 6.05Renaud LAVILLENIE FRA Eugene 30.05.15 7 Paweł WOJCIECHOWSKI POL 5.91 5.84 8 Raphael HOLZDEPPE GER 5.94 5.94 2015 World Outdoor list 9 Shawn BARBER CAN 5.93 5.93 6.05Renaud LAVILLENIE FRA Eugene 30.05.15 5.94Raphael HOLZDEPPE GER Nürnberg 26.07.15 5.93Shawn BARBER CAN London 25.07.15 Medal Winners Zürich previous Winners 5.92Thiago BRAZ BRA Baku 24.06.15 2015 - Beijing IAAF World Ch. 12 Renaud LAVILLENIE (FRA) 5.70 5.91Konstantinos FILIPPIDIS GRE Paris 04.07.15 1. Shawn BARBER (CAN) 5.90 07 Igor PAVLOV (RUS) 5.75 5.84Paweł WOJCIECHOWSKI POL Lausanne 09.07.15 2. Raphael HOLZDEPPE (GER) 5.90 06 Brad WALKER (USA) 5.85 5.82Sam KENDRICKS USA Des Moines 25.04.15 3. -

Structural Exploration of a Fabrication-Aware Design Space with Marionettes Meshes Romain Mesnil, Cyril Douthe, Olivier Baverel, Christiane Richter, Bruno Leger
Structural exploration of a fabrication-aware design space with Marionettes Meshes Romain Mesnil, Cyril Douthe, Olivier Baverel, Christiane Richter, Bruno Leger To cite this version: Romain Mesnil, Cyril Douthe, Olivier Baverel, Christiane Richter, Bruno Leger. Structural explo- ration of a fabrication-aware design space with Marionettes Meshes. IASS Annual Symposium 2016: Spatial Structures in the 21st Century, Sep 2016, Tokyo, Japan. hal-01978811 HAL Id: hal-01978811 https://hal.archives-ouvertes.fr/hal-01978811 Submitted on 11 Jan 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. See discussions, stats, and author profiles for this publication at: https://www.researchgate.net/publication/308698359 Structural explorations of a fabrication-aware design space with marionette meshes Conference Paper · September 2016 CITATIONS READS 3 260 5 authors, including: Romain Mesnil Christiane Richter École des Ponts ParisTech Technische Universität München 28 PUBLICATIONS 106 CITATIONS 3 PUBLICATIONS 3 CITATIONS SEE PROFILE SEE PROFILE Olivier Baverel École des Ponts ParisTech 142 PUBLICATIONS 842 CITATIONS SEE PROFILE Some of the authors of this publication are also working on these related projects: thinkshell.fr View project Large scale additive manufacturing View project All content following this page was uploaded by Romain Mesnil on 03 October 2016. -

An Exploration of 3D Printing Design Space Inspired by Masonry Paul Carneau, Romain Mesnil, Nicolas Roussel, Olivier Baverel
An exploration of 3d printing design space inspired by masonry Paul Carneau, Romain Mesnil, Nicolas Roussel, Olivier Baverel To cite this version: Paul Carneau, Romain Mesnil, Nicolas Roussel, Olivier Baverel. An exploration of 3d printing design space inspired by masonry. IASS Symposium 2019, ”Form and Force”, Oct 2019, Barcelona, Spain. 10.5281/zenodo.3563672. hal-02385258 HAL Id: hal-02385258 https://hal.archives-ouvertes.fr/hal-02385258 Submitted on 28 Nov 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Proceedings of the IASS Annual Symposium 2019 - Structural Membranes 2019 Form and Force 7-10 October 2019, Barcelona, Spain C. L´azaro,K.-U. Bletzinger, E. O~nate(eds.) An exploration of 3d printing design space inspired by masonry Paul CARNEAUa, Romain MESNILb, Nicolas ROUSSELa, Olivier BAVERELa;c;d a Navier, UMR 8205, Ecole´ des Ponts, IFSTTAR, CNRS, UPE, Champs-sur-Marne, France [email protected] b Ecole´ des Ponts ParisTech, Champs-sur-Marne, France c ENSA Paris-Malaquais, Laboratoire Gometrie Structure Architecture, France d ENSA Grenoble, France Abstract This paper describes an approach of a process-aware exploration of the design space of building components constructed by extrusion of cementitious material (or concrete 3d printing). -

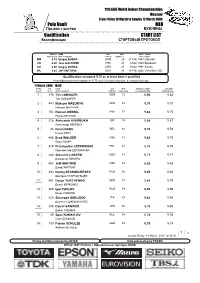
0 Sl Round 2L
11th IAAF World Indoor Championships Moscow From Friday 10 March to Sunday 12 March 2006 Pole Vault MEN Прыжок с шестом МУЖЧИНЫ ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHL Final START LIST Финал СТАРТОВЫЙ ПРОТОКОЛ ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETI RESULT NAME NAT AGE DATE VENUE РЕЗУЛЬТАТ ИМЯ, ФАМИЛИЯ СТРАНА ВОЗРАСТ ДАТА ГОРОД WR6.15 Sergey BUBKA UKR 2921 Feb 1993 Donetsk CR6.00 Jean GALFIONE FRA 276 Mar 1999 Maebashi CR6.00 Sergey BUBKA URS 279 Mar 1991 Sevilla WL5.85 Jeff HARTWIG USA 3818 Feb 2006 Vermillion, SD 12 March 2006 16:00 START BIB NAME NAT YEAR PERSONAL BEST 2006 BEST № П/П № УЧ. ИМЯ, ФАМИЛИЯ СТРАНА ГОД РОЖД. ЛИЧНЫЙ РЕКОРД РЕКОРД 2006 1 486 Brad WALKER USA 81 5.83 5.75 Брэд УОКЕР 2 451 Denys YURCHENKO UKR 78 5.85 5.70 Денис ЮРЧЕНКО 3 286 Giovanni LANARO MEX 81 5.71 5.71 Джованни ЛАНАРО 4 180 Fabian SCHULZE GER 84 5.75 5.75 Фабиан ШУЛЬЦЕ 5 216 Aleksandr AVERBUKH ISR 74 5.86 5.81 Александр АВЕРБУХ 6 176 Tim LOBINGER GER 72 5.95 5.82 Тим ЛОБИНГЕР 7 462 Jeff HARTWIG USA 67 6.02 5.85 Джеф ХАРТВИГ 8 413 Alhaji JENG SWE 81 5.80 5.80 Алхаджи ДЖЕНГ SERIES 5.50 5.60 5.65 5.70 5.75 ПОРЯДОК ПОДЪЕМА ВЫСОТ WORLD ALL-TIME WORLD TOP 2006 МИРОВОЙ ТОП-ЛИСТ ЗА ВСЕ ГОДЫ МИРОВОЙ ТОП-ЛИСТ 2006 RESULT NAME -

Free-Form Structures from Topologically Interlocking Masonries Vianney Loing, Olivier Baverel, Jean-François Caron, Romain Mesnil
Free-form structures from topologically interlocking masonries Vianney Loing, Olivier Baverel, Jean-François Caron, Romain Mesnil To cite this version: Vianney Loing, Olivier Baverel, Jean-François Caron, Romain Mesnil. Free-form structures from topologically interlocking masonries. Automation in Construction, Elsevier, 2020, 113, pp.103117. 10.1016/j.autcon.2020.103117. hal-03026528 HAL Id: hal-03026528 https://hal.archives-ouvertes.fr/hal-03026528 Submitted on 26 Nov 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Free-form structures from topologically interlocking masonries Vianney Loinga, Olivier Baverela, Jean-Fran¸coisCarona,∗, Romain Mesnila aLaboratoire Navier, UMR 8205, Ecole´ des Ponts, IFSTTAR, CNRS, UPE, Marne-La-Vall´ee,France Abstract The paper presents new results about the geometry of topological interlocking masonries and some possibilities they present to build without formwork. Construction without the use of formwork may be an important issue concerning both productivity increase and decreasing of waste generated on a construction site. Due to the development of compu- tational design and robotics in the construction industry, it makes sense to (re)explore innovative design and process of complex masonry structures. The design of this kind of masonry is standard for planar structures, and in this paper, a generalization is proposed for the parametric design of curved structures. -

2019 World Championships Statistics - Men’S PV by K Ken Nakamura
2019 World Championships Statistics - Men’s PV by K Ken Nakamura The records to look for in Doha: 1) Lavillenie, if he wins, will be the first Frenchman to win this event. He will then have gold at all major championships, Worlds, Olympics, World Indoor and European. He will also be the second (after Tarasov) to have complete set of medals. 2) If Duplantis wins either gold or silver, it will be the best medal for SWE. Summary: All time Performance List at the World Championships Performance Performer Height Name Nat Pos Venue Year 1 1 6.05 Dmitri Markov AUS 1 Edmonton 2001 2 2 6.02 Maksim Tarasov RUS 1 Sevilla 1999 3 3 6.01 Sergey Bubka UKR 1 Athinai 1997 4 6.00 Sergey Bubka 1 Stuttgart 1993 5 5.96 Maksim Tarasov 2 Athinai 19 97 6 5.95 Sergey Bubka 1 Tokyo 1991 6 4 5.95 Sam Kendricks USA 1 London 2017 8 5.92 Sergey Bubka 1 Göteborg 1995 9 5 5.91 Dean Starkey USA 3 Athinai 1997 Margin of Victory Difference Height Name Nat Venue Year Max 20cm 6.05m Dmitri Markov AUS Edmonton 2001 Min 0cm 5.86m Brad Walker USA Osaka 2007 5.90m Pawel Wojciechowski POL Daegu 2011 5.89m Raphael Holzdeppe GER Moskva 2013 5.90m Shawn Barber CAN Beijing 2015 Best Marks for Places in the World Championships Pos Height Name Nat Venue Year 1 6.05 Dmitri Markov AUS Edmonton 2001 2 5.96 Maksim Tarasov RUS Athinai 1997 3 5.91 Dean Starkey USA Athinai 1997 4 5.85 Rodion Gataulin URS Tokyo 1991 Michael Stolle GER Edmonton 2001 Dmitri Markov AUS Paris 2003 Lukasz Michalski POL Daegu 2011 Multiple Medalists: Renaud Lavillenie (FRA): 2009 Bronze, 2011 Bronze, 2013 Silver, -
0 Sl Round 2L
11th IAAF World Indoor Championships Moscow From Friday 10 March to Sunday 12 March 2006 Pole Vault MEN Прыжок с шестом МУЖЧИНЫ ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHL Qualification START LIST Квалификация СТАРТОВЫЙ ПРОТОКОЛ ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETI RESULT NAME NAT AGE DATE VENUE РЕЗУЛЬТАТ ИМЯ, ФАМИЛИЯ СТРАНА ВОЗРАСТ ДАТА ГОРОД WR6.15 Sergey BUBKA UKR 2921 Feb 1993 Donetsk CR6.00 Jean GALFIONE FRA 276 Mar 1999 Maebashi CR6.00 Sergey BUBKA URS 279 Mar 1991 Sevilla WL5.85 Jeff HARTWIG USA 3818 Feb 2006 Vermillion, SD Qualification standard 5.70 or at least best 8 qualified Квалификационный норматив 5.70 или 8 лучших выходят в следующий круг 11 March 2006 10:00 START BIB NAME NAT YEAR PERSONAL BEST 2006 BEST № П/П № УЧ. ИМЯ, ФАМИЛИЯ СТРАНА ГОД РОЖД. ЛИЧНЫЙ РЕКОРД РЕКОРД 2006 1 176 Tim LOBINGER GER 72 5.95 5.82 Тим ЛОБИНГЕР 2 443 Maksym MAZURYK UKR 83 5.70 5.70 Максим МАЗУРИК 3 152 Romain MESNIL FRA 77 5.86 5.75 Ромэн МЕСНИЛ 4 216 Aleksandr AVERBUKH ISR 74 5.86 5.81 Александр АВЕРБУХ 5 24 Kevin RANS BEL 82 5.70 5.70 Кевин РАНС 6 486 Brad WALKER USA 81 5.83 5.75 Брэд УОКЕР 7 318 Przemyslaw CZERWINSKI POL 83 5.70 5.70 Пржемислав ШЕРВИНСКИ 8 286 Giovanni LANARO MEX 81 5.71 5.71 Джованни -

Weekly Release
WASHINGTON TRACK AND FIELD Jan. 14, 2003 //For Immediate Release// Contact: Brian Beaky Husky Track and Field Opens 2004 Season 2004 Husky Track Schedule Indoor With First of Five Meets at Dempsey Indoor Date Meet Location Jan. 17 Husky Indoor Preview Seattle On the Track: Washington’s track and field teams seek to recapture the magic of an Jan. 31 UW Invitational Seattle exciting 2003 season on Saturday with the season-opening UW Indoor Preview at Feb. 7 Bronco Invitational Boise, Idaho Dempsey Indoor. With six of the team’s 11 NCAA Championships qualifiers returning, Feb. 14 Pac-10 Invitational Seattle and a recruiting class that boasts numerous prep and junior-college All-Americans, the Feb. 27-28 MPSF Championships Seattle Huskies will attempt to put together a fitting follow-up to the team’s 2003 campaign, Mar. 6 UW Last Chance Qualifier Seattle which featured one national champion, four All-Americans and a dozen school records. Mar. 12-13 NCAA Champs. Fayetteville, Ark. No fewer than 42 Division-I, small-college and club squads will be helping Washington Outdoor ring in 2004 on Saturday, including full teams from Oregon, Stanford, Sacramento State, Date Meet Location and Portland. Spectator seating is available for all events, and admission is free. Mar. 20 Cal Poly Invite San Luis Obispo, CA Mar. 26-27 Stanford Invitational Palo Alto, CA Vaulters Tune Up: Washington’s vaulters earned a jump-start on 2004 at last wekend’s Mar. 31-Apr.4 Texas Relays Austin, TX U.S. Pole Vault Summit in Reno, Nev. Senior All-American Brad Walker, who saw bid Apr. -

Shanghai 2018
Men's 100m Diamond Discipline 12.05.2018 Start list 100m Time: 20:53 Records Lane Athlete Nat NR PB SB 1 Isiah YOUNG USA 9.69 9.97 10.02 WR 9.58 Usain BOLT JAM Berlin 16.08.09 2 Andre DE GRASSE CAN 9.84 9.91 10.15 AR 9.91 Femi OGUNODE QAT Wuhan 04.06.15 AR 9.91 Femi OGUNODE QAT Gainesville 22.04.16 3 Justin GATLIN USA 9.69 9.74 10.05 NR 9.99 Bingtian SU CHN Eugene 30.05.15 4 Bingtian SU CHN 9.99 9.99 10.28 NR 9.99 Bingtian SU CHN Beijing 23.08.15 5 Chijindu UJAH GBR 9.87 9.96 10.08 WJR 9.97 Trayvon BROMELL USA Eugene 13.06.14 6 Ramil GULIYEV TUR 9.92 9.97 MR 9.69 Tyson GAY USA 20.09.09 7 Yoshihide KIRYU JPN 9.98 9.98 DLR 9.69 Yohan BLAKE JAM Lausanne 23.08.12 8 Zhenye XIE CHN 9.99 10.04 SB 9.97 Ronnie BAKER USA Torrance 21.04.18 9 Reece PRESCOD GBR 9.87 10.03 10.39 2018 World Outdoor list 9.97 +0.5 Ronnie BAKER USA Torrance 21.04.18 Medal Winners Shanghai previous 10.01 +0.8 Zharnel HUGHES GBR Kingston 24.02.18 10.02 +1.9 Isiah YOUNG USA Des Moines, IA 28.04.18 2017 - London IAAF World Ch. in Winners 10.03 +0.8 Akani SIMBINE RSA Gold Coast 09.04.18 Athletics 17 Bingtian SU (CHN) 10.09 10.03 +1.9 Michael RODGERS USA Des Moines, IA 28.04.18 1. -

Communiqué De Presse N°4 Lundi 21 Août 2006 Indécis Et Passionnant L
Communiqué de presse N°4 Lundi 21 août 2006 Indécis et passionnant L’équipe de France se présentera en force, samedi 26 août 2006, pour la deuxième édition du SEAT DécaNation. Mais elle aura fort à faire pour inscrire son nom au palmarès, l’adversité s’annoncant redoutable. Les Etats-Unis, l’Allemagne, la Russie, l’Espagne, la Chine, l’Ukraine et la Pologne ont répondu cette année à l’invitation de la Fédération française d’athlétisme, conceptrice et organisatrice de l’évènement. Et aucune de ces sept nations n’entend faire de la figuration sur la piste du stade Charléty, comme en témoigne la composition de leurs équipes. L’an passé, la sélection américaine avait semblé un peu tendre pour espérer inaugurer le palmarès de la compétition. Cette fois, elle fait plaisir à voir. Chez les hommes, elle sera emmenée par Otis Harris, champion olympique du 4x400 m à Athènes, et Reese Hoffa, champion du monde en salle du lancers du poids, l’hiver dernier à Moscou. Sa sélection féminine est articulée autour d’un solide trio, formé de Jenny Adams (12’’66 au 100 m haies cette saison), Amy Acuff (4ème du saut en hauteur aux Jeux d’Athènes), et Tianna Madison, surprenante championne du monde de la longueur l’été dernier à Helsinki. La Russie a démontré, en début de mois à Göteborg, que l’Europe était devenue trop petite pour ses athlètes, rentrés avec 34 médailles. Elle fera figure d’épouvantail, à Charléty, même privée de ses récentes championnes d’Europe. Yekaterina Volkova (9’20’’49 au 3000 m steeple en 2005), Yekaterina Khoroshikh (76,63 m au marteau), Dimitriy Sapinskiy (8,17 m en longueur), et Vadim Khersontsev (78,54 m au marteau), ne viseront qu’une seule place, la première. -
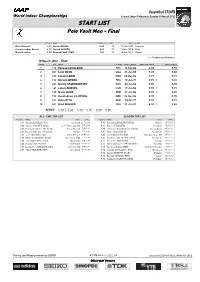
START LIST Pole Vault Men - Final
Istanbul (TUR) World Indoor Championships From Friday 9 March to Sunday 11 March 2012 START LIST Pole Vault Men - Final RESULT NAME COUNTRY AGE DATE VENUE World Record 6.15 Sergey BUBKA UKR 29 21 Feb 1993 Donetsk Championships Record 6.01 Steven HOOKER AUS 27 13 Mar 2010 Doha World Leading 5.93 Renaud LAVILLENIE FRA 25 18 Feb 2012 Nevers o = Outdoor performance 10 March 2012 17:00 ORDER BIB NAME COUNTRY DATE of BIRTH PERSONAL BEST SEASON BEST 1 110 Renaud LAVILLENIE FRA 18 Sep 86 6.03 5.93 2 331 Scott ROTH USA 25 Jun 88 5.72 5.60 3 127 Steven LEWIS GBR 20 May 86 5.77 5.77 4 112 Romain MESNIL FRA 13 Jun 77 5.95 o 5.72 5 261 Dmitry STARODUBTSEV RUS 03 Jan 86 5.90 5.90 6 61 Lázaro BORGES CUB 19 Jun 86 5.90 o 5.72 7 140 Malte MOHR GER 27 Jun 86 5.90 o 5.87 8 152 Konstadínos FILIPPÍDIS GRE 26 Nov 86 5.75 5.75 9 141 Björn OTTO GER 16 Oct 77 5.92 5.92 10 341 Brad WALKER USA 21 Jun 81 6.04 o 5.86 SERIES 5.50 5.60 5.70 5.75 5.80 5.85 ALL-TIME TOP LIST SEASON TOP LIST RESULT NAME Venue DATE RESULT NAME Venue DATE 6.15 Sergey BUBKA (UKR) Donetsk 21 Feb 93 5.93 Renaud LAVILLENIE (FRA) Nevers 18 Feb 12 6.06 Steven HOOKER (AUS) Boston (Roxbury), MA 7 Feb 09 5.92 Björn OTTO (GER) Potsdam 18 Feb 12 6.03 Renaud LAVILLENIE (FRA) Paris (Bercy) 5 Mar 11 5.90 Dmitry STARODUBTSEV (RUS) Chelyabinsk 29 Dec 11 6.02 Radion GATAULLIN (URS) Gomel 4 Feb 89 5.87 Malte MOHR (GER) Karlsruhe 26 Feb 12 6.02 Jeff HARTWIG (USA) Sindelfingen 10 Mar 02 5.86 Brad WALKER (USA) Albuquerque, NM 26 Feb 12 6.00 Maksim TARASOV (RUS) Budapest (SC) 5 Feb 99 5.82 Raphael HOLZDEPPE