1.3 the Secant Method
1 Chapter 1
1.3 The Secant Method
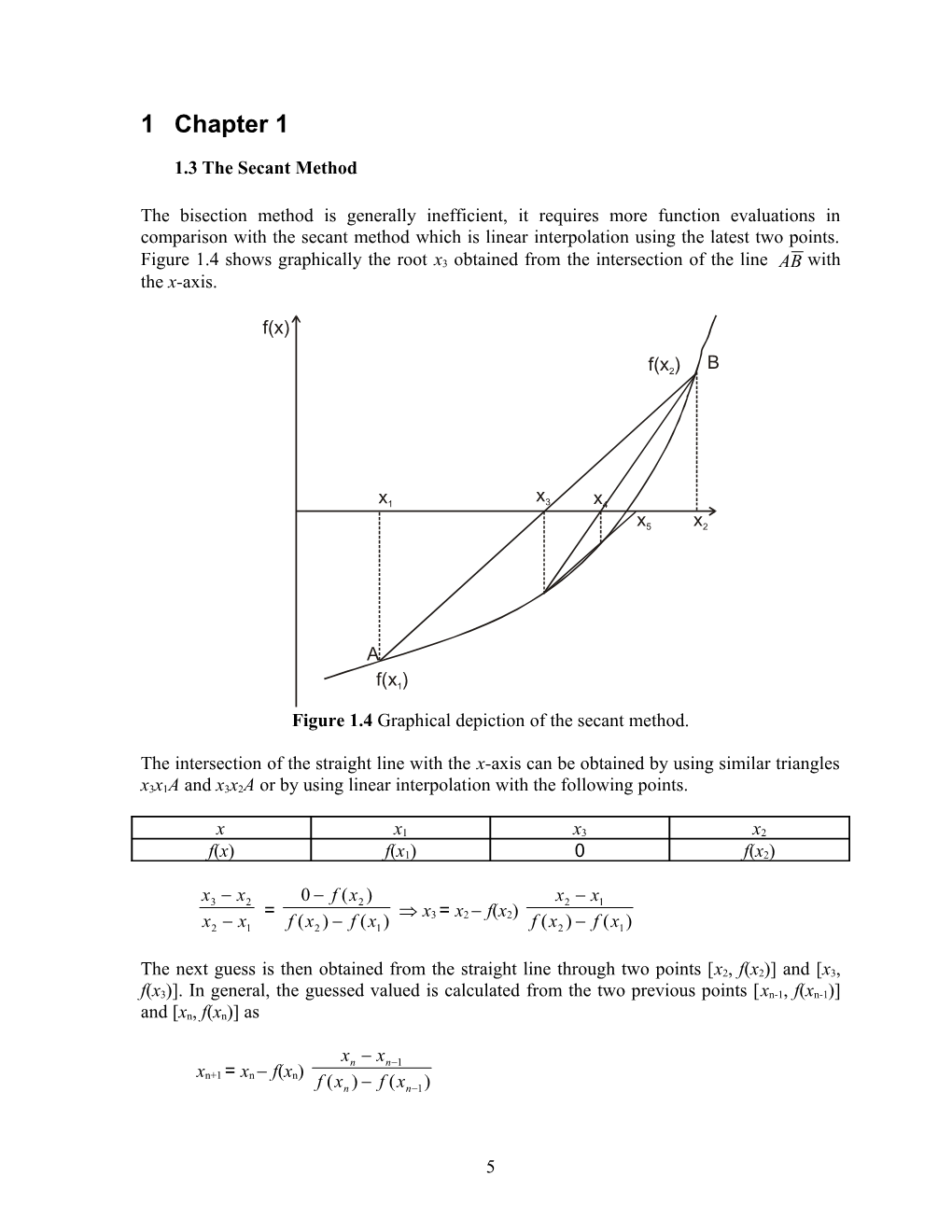
The bisection method is generally inefficient, it requires more function evaluations in comparison with the secant method which is linear interpolation using the latest two points. Figure 1.4 shows graphically the root x3 obtained from the intersection of the line with the x-axis.
Figure 1.4 Graphical depiction of the secant method.
The intersection of the straight line with the x-axis can be obtained by using similar triangles x3x1A and x3x2A or by using linear interpolation with the following points.
x / x1 / x3 / x2f(x) / f(x1) / 0 / f(x2)
= Þ x3 = x2 - f(x2)
The next guess is then obtained from the straight line through two points [x2, f(x2)] and [x3, f(x3)]. In general, the guessed valued is calculated from the two previous points [xn-1, f(xn-1)] and [xn, f(xn)] as
xn+1 = xn - f(xn)
The secant method always uses the latest two points without the requirement that they bracket the root as shown in Figure 1.4 for points [x3, f(x3)] and [x4, f(x4)]. As a consequence, the secant method can sometime diverge. A Matlab program for the secant method is listed in Table 1.2 where the function f(x) is an input to the program. The statement eval(f) is used to evaluate the function at a given value of x.
Table 1.2 ______
% Secant method
f=input('f(x)=','s');
tol=input('error tolerance =1e-5, new tolerance=');
if length(tol)==0,tol=1e-5;end
x1=input(' First guess=');
x=x1;
f1=eval(f);
x2=input(' Second guess=');
x=x2;
f2=eval(f);xsave=x2;
disp(' Secant method')
for i=2:21
x=x2-f2*(x2-x1)/(f2-f1);
fx=eval(f);
x1=x2;f1=f2;ex=abs(x2-x);
x2=x;f2=fx;
fprintf('i = %g, x = %g, fx = %g\n',i,x,fx)
if ex<tol, break,end
end
1.4 The False-Position Method
The false-position method is also a linear interpolation method, however is based on the previous two points that bracket the roots. Figure 1.5 shows graphically the root x3 obtained from the intersection of the line with the x-axis. This root is no different from the value obtained from the secant method. The next guess x4 is then obtained from the straight line through two points [x2, f(x2)] and [x3, f(x3)] since these two previous points also bracket the roots. However, for the next iteration, x5 is obtained from the two latest points [x2, f(x2)] and [x4, f(x4)] that bracket the root. The second method uses [x3, f(x3)] and [x4, f(x4)]. The false-position method always converges however the convergence can be slow if the solution is approached from one side of the root.
A Matlab program for the false-position method is listed in Table 1.3 where the function f(x) is an input to the program. The statement eval(f) is used to evaluate the function at a given value of x. The iteration will not start if the first two guesses do not bracket the root.
Figure 1.5 Graphical depiction of the false-position method.
Table 1.3 ______
% False Position method
f=input('f(x)=','s');
tol=input('error tolerance =1e-5, new tolerance=');
if length(tol)==0,tol=1e-5;end
x1=input(' First guess=');
x=x1;
f1=eval(f);
x2=input(' Second guess=');
x=x2;
f2=eval(f);xsave=x2;
if f1*f2<0
disp(' False Position ')
for i=2:21
x=x2-f2*(x2-x1)/(f2-f1);
fx=eval(f);
if fx*f1>0
x1=x;f1=fx;
else
x2=x;f2=fx;
end
fprintf('i = %g, x = %g, fx = %g\n',i,x,fx)
if abs(xsave-x)<tol, break,end
xsave=x;
end
else
disp('Need to bracket the roots')
end
1.5 The Newton-Raphson Method
The Newton-Raphson method and its modification is probably the most widely used of all root-finding methods. Starting with an initial guess x1 at the root, the next guess x2 is the intersection of the tangent from the point [x1, f(x1)] to the x-axis. The next guess x3 is the intersection of the tangent from the point [x2, f(x2)] to the x-axis as shown in Figure 1.6. The process can be repeated until the desired tolerance is attained.
Figure 1.6 Graphical depiction of the Newton-Raphson method.
The Newton-Raphson method can be derived from the definition of a slope
f’(x1) = Þ x2 = x1 -
In general, from the point [xn, f(xn)], the next guess is calculated as
xn+1 = xn -
The derivative or slope f(xn) can be approximated numerically as
f’(xn) =
Example 1.2
Solve f(x) = x3 + 4x2 - 10 using the the Newton-Raphson method for a root in [1, 2].
Solution
From the formula xn+1 = xn -
f(xn) = + 4- 10 Þ f’(xn) = 3 + 8xn
xn+1 = xn -
Using the initial guess, xn = 1.5, xn+1 is estimated as
xn+1 = 1.5 - = 1.3733
A Matlab program for the Newton-Raphson method is listed in Table 1.4 where the function f(x) is an input to the program. The statement eval(f) is used to evaluate the function at a given value of x. The derivative is evaluated numerically using f’(xn) =
with Dx = 0.01. A sample result is given at the end of the program.
Table 1.4 ______
% Newton method with numerical derivative
f=input('f(x)=','s');
tol=input('error tolerance =1e-5, new tolerance=');
if length(tol)==0,tol=1e-5;end
x1=input(' First guess=');
x=x1; fx=eval(f);
for i=1:100
if abs(fx)<tol, break,end
x=x+.01;
ff=eval(f);
fdx=(ff-fx)/.01;
x1=x1-fx/fdx;
x=x1;
fx=eval(f);
fprintf('i = %g, x = %g, fx = %g\n',i,x,fx)
end
f(x)=x^3+4*x^2-10
error tolerance =1e-5, new tolerance=
First guess=1.5
i = 1, x = 1.37391, fx = 0.143874
i = 2, x = 1.36531, fx = 0.00129871
i = 3, x = 1.36523, fx = 6.39291e-006
1-8