A Three-Dimensional Model for Arterial Tree Representation, Generated by Constrained Constructive Optimization
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Evaluation of Artery Visualizations for Heart Disease Diagnosis
Evaluation of Artery Visualizations for Heart Disease Diagnosis Michelle A. Borkin, Student Member, IEEE, Krzysztof Z. Gajos, Amanda Peters, Dimitrios Mitsouras, Simone Melchionna, Frank J. Rybicki, Charles L. Feldman, and Hanspeter Pfister, Senior Member, IEEE Fig. 1. Left: Traditional 2D projection (A) of a single artery, and 3D representation (C) of a right coronary artery tree with a rainbow color map. Right: 2D tree diagram representation (B) and equivalent 3D representation (D) of a left coronary artery tree with a diverging color map. Abstract—Heart disease is the number one killer in the United States, and finding indicators of the disease at an early stage is critical for treatment and prevention. In this paper we evaluate visualization techniques that enable the diagnosis of coronary artery disease. A key physical quantity of medical interest is endothelial shear stress (ESS). Low ESS has been associated with sites of lesion formation and rapid progression of disease in the coronary arteries. Having effective visualizations of a patient’s ESS data is vital for the quick and thorough non-invasive evaluation by a cardiologist. We present a task taxonomy for hemodynamics based on a formative user study with domain experts. Based on the results of this study we developed HemoVis, an interactive visualization application for heart disease diagnosis that uses a novel 2D tree diagram representation of coronary artery trees. We present the results of a formal quantitative user study with domain experts that evaluates the effect of 2D versus 3D artery representations and of color maps on identifying regions of low ESS. We show statistically significant results demonstrating that our 2D visualizations are more accurate and efficient than 3D representations, and that a perceptually appropriate color map leads to fewer diagnostic mistakes than a rainbow color map. -

Vessels and Circulation
CARDIOVASCULAR SYSTEM OUTLINE 23.1 Anatomy of Blood Vessels 684 23.1a Blood Vessel Tunics 684 23.1b Arteries 685 23.1c Capillaries 688 23 23.1d Veins 689 23.2 Blood Pressure 691 23.3 Systemic Circulation 692 Vessels and 23.3a General Arterial Flow Out of the Heart 693 23.3b General Venous Return to the Heart 693 23.3c Blood Flow Through the Head and Neck 693 23.3d Blood Flow Through the Thoracic and Abdominal Walls 697 23.3e Blood Flow Through the Thoracic Organs 700 Circulation 23.3f Blood Flow Through the Gastrointestinal Tract 701 23.3g Blood Flow Through the Posterior Abdominal Organs, Pelvis, and Perineum 705 23.3h Blood Flow Through the Upper Limb 705 23.3i Blood Flow Through the Lower Limb 709 23.4 Pulmonary Circulation 712 23.5 Review of Heart, Systemic, and Pulmonary Circulation 714 23.6 Aging and the Cardiovascular System 715 23.7 Blood Vessel Development 716 23.7a Artery Development 716 23.7b Vein Development 717 23.7c Comparison of Fetal and Postnatal Circulation 718 MODULE 9: CARDIOVASCULAR SYSTEM mck78097_ch23_683-723.indd 683 2/14/11 4:31 PM 684 Chapter Twenty-Three Vessels and Circulation lood vessels are analogous to highways—they are an efficient larger as they merge and come closer to the heart. The site where B mode of transport for oxygen, carbon dioxide, nutrients, hor- two or more arteries (or two or more veins) converge to supply the mones, and waste products to and from body tissues. The heart is same body region is called an anastomosis (ă-nas ′tō -mō′ sis; pl., the mechanical pump that propels the blood through the vessels. -

Vascular Anomalies Compressing the Oesophagus and Trachea
Thorax: first published as 10.1136/thx.24.3.295 on 1 May 1969. Downloaded from T7horax (1969), 24, 295. Vascular anomalies compressing the oesophagus and trachea J. C. R. LINCOLN, P. B. DEVERALL, J. STARK, E. ABERDEEN, AND D. J. WATERSTON From the Hospital for Sick Children, Great Ormond Street, London W.C.I Vascular rings formed by anomalies of major arteries can compress the trachea and oesophagus so much as to cause respiratory distress and dysphagia. Twenty-nine patients with this condition are reviewed and discussed in five groups. The symptoms and signs are noted. Radiological examination by barium swallow is the most useful diagnostic aid. Symptoms can only be relieved by operation. The trachea is often deformed at the site of the constricting ring. Only infrequently is there immediate relief from the pre-operative symptoms. Two babies were successfully treated for an aberrant left pulmonary artery. The diagnosis and treatment of major arterial DOUBLE AORTIC ARCH Nineteen children were anomalies which cause compression of the oeso- treated for some form of double aortic arch. Their phagus and trachea are now well established. age at operation ranged from 1 week to 11 months, Although an aberrant right subclavian artery was but the majority were treated at about the age of described in 1794 by Bayford (Fig. 1), who gave 5 to 6 months (Fig. 2). Frequently the presenting the detailed post-mortem finding in a woman who symptoms had been noticed since birth but for had died from starvation secondary to this varying reasons there was delay in making the http://thorax.bmj.com/ anomaly, and a double aortic arch was described correct diagnosis. -

Artery/Vein Classification of Blood Vessel Tree in Retinal Imaging
Artery/vein Classification of Blood Vessel Tree in Retinal Imaging Joaquim de Moura1, Jorge Novo1, Marcos Ortega1, Noelia Barreira1 and Pablo Charlon´ 2 1Departamento de Computacion,´ Universidade da Coruna,˜ A Coruna,˜ Spain 2Instituto Oftalmologico´ Victoria de Rojas, A Coruna,˜ Spain joaquim.demoura, jnovo, mortega, nbarreira @udc.es, [email protected] { } Keywords: Retinal Imaging, Vascular Tree, Segmentation, Artery/vein Classification. Abstract: Alterations in the retinal microcirculation are signs of relevant diseases such as hypertension, arteriosclerosis, or diabetes. Specifically, arterial constriction and narrowing were associated with early stages of hypertension. Moreover, retinal vasculature abnormalities may be useful indicators for cerebrovascular and cardiovascular diseases. The Arterio-Venous Ratio (AVR), that measures the relation between arteries and veins, is one of the most referenced ways of quantifying the changes in the retinal vessel tree. Since these alterations affect differently arteries and veins, a precise characterization of both types of vessels is a key issue in the development of automatic diagnosis systems. In this work, we propose a methodology for the automatic vessel classification between arteries and veins in eye fundus images. The proposal was tested and validated with 19 near-infrared reflectance retinographies. The methodology provided satisfactory results, in a complex domain as is the retinal vessel tree identification and classification. 1 INTRODUCTION Hence, direct analysis of many injuries caused by oc- ular pathologies can be achieved, as is the case, for The analysis of the eye fundus offers useful infor- example, the diabetic retinopathy (DR). The DR is a mation about the status of the different structures the diabetes mellitus complication, one of the principal human visual system integrates, as happens with the causes of blindness in the world (Pascolini, 2011). -

The Inferior Epigastric Artery: Anatomical Study and Clinical Significance
Int. J. Morphol., 35(1):7-11, 2017. The Inferior Epigastric Artery: Anatomical Study and Clinical Significance Arteria Epigástrica Inferior: Estudio Anatómico y Significancia Clínica Waseem Al-Talalwah AL-TALALWAH, W. The inferior epigastric artery: anatomical study and clinical significance. Int. J. Morphol., 35(1):7-11, 2017. SUMMARY: The inferior epigastric artery usually arises from the external iliac artery. It may arise from different origin. The aim of current study is to provide sufficient date of the inferior epigastric artery for clinician, radiologists, surgeons, orthopaedic surgeon, obstetricians and gynaecologists. The current study includes 171 dissected cadavers (92 male and 79 female) to investigate the origin and branch of the inferior epigastric artery in United Kingdom population (Caucasian) as well as in male and female. The inferior epigastric artery found to be a direct branch arising independently from the external iliac artery in 83.6 %. Inferior epigastric artery arises from common trunk of external iliac artery with the obturator artery or aberrant obturator artery in 15.1 % or 1.3 %. Further, the inferior epigastric artery gives obturator and aberrant obturator branch in 3.3 % and 0.3 %. Therefore, the retropubic connection vascularity is 20 % which is more in female than male. As the retropubic region includes a high vascular variation, a great precaution has to be considered prior to surgery such as hernia repair, internal fixation of pubic fracture and skin flap transplantation. The radiologists have to report treating physicians to decrease intra-pelvic haemorrhage due to iatrogenic lacerating obturator or its accessory artery KEY WORDS: Inferior epigastric; Obturator; Aberrant Oburator; Accessory Obturator; Hernia; Corona Mortis; Pubic fracture. -

Screening for Carotid Artery Stenosis
Understanding Task Force Recommendations Screening for Carotid Artery Stenosis The U.S. Preventive Services Task Force (Task Force) The final recommendation statement summarizes has issued a final recommendation statement on what the Task Force learned about the potential Screening for Carotid Artery Stenosis. benefits and harms of screening for carotid artery stenosis: Health professionals should not screen the This final recommendation statement applies to general adult population. adults who do not have signs or symptoms of a stroke and who have not already had a stroke or a This fact sheet explains this recommendation and transient ischemic attack (a “mini-stroke”). People what it might mean for you. with signs or symptoms of a stroke should see their doctor immediately. Carotid artery stenosis is the narrowing of the arteries that run along each What is carotid side of the neck. These arteries provide blood flow to the brain. Over time, plaque (a fatty, waxy substance) can build up and harden the arteries, artery stenosis? limiting the flow of blood to the brain. Facts About Carotid Artery Stenosis Carotid artery stenosis is one of many risk factors for stroke, a leading cause of death and disability in the United States. However, carotid artery stenosis is uncommon—about ½ to 1% of the population have the condition. The main risk factors are older age, being male, high blood pressure, smoking, high blood cholesterol, diabetes, and heart disease. Screening and Treatment for Carotid Artery Stenosis Carotid artery stenosis screening is often done using ultrasound, a painless test that uses sound waves to create a picture of the carotid arteries. -

Blood Vessels and Circulation
19 Blood Vessels and Circulation Lecture Presentation by Lori Garrett © 2018 Pearson Education, Inc. Section 1: Functional Anatomy of Blood Vessels Learning Outcomes 19.1 Distinguish between the pulmonary and systemic circuits, and identify afferent and efferent blood vessels. 19.2 Distinguish among the types of blood vessels on the basis of their structure and function. 19.3 Describe the structures of capillaries and their functions in the exchange of dissolved materials between blood and interstitial fluid. 19.4 Describe the venous system, and indicate the distribution of blood within the cardiovascular system. © 2018 Pearson Education, Inc. Module 19.1: The heart pumps blood, in sequence, through the arteries, capillaries, and veins of the pulmonary and systemic circuits Blood vessels . Blood vessels conduct blood between the heart and peripheral tissues . Arteries (carry blood away from the heart) • Also called efferent vessels . Veins (carry blood to the heart) • Also called afferent vessels . Capillaries (exchange substances between blood and tissues) • Interconnect smallest arteries and smallest veins © 2018 Pearson Education, Inc. Module 19.1: Blood vessels and circuits Two circuits 1. Pulmonary circuit • To and from gas exchange surfaces in the lungs 2. Systemic circuit • To and from rest of body © 2018 Pearson Education, Inc. Module 19.1: Blood vessels and circuits Circulation pathway through circuits 1. Right atrium (entry chamber) • Collects blood from systemic circuit • To right ventricle to pulmonary circuit 2. Pulmonary circuit • Pulmonary arteries to pulmonary capillaries to pulmonary veins © 2018 Pearson Education, Inc. Module 19.1: Blood vessels and circuits Circulation pathway through circuits (continued) 3. Left atrium • Receives blood from pulmonary circuit • To left ventricle to systemic circuit 4. -
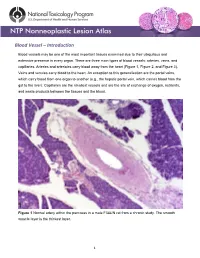
Blood Vessel – Introduction
Blood Vessel – Introduction Blood vessels may be one of the most important tissues examined due to their ubiquitous and extensive presence in every organ. There are three main types of blood vessels: arteries, veins, and capillaries. Arteries and arterioles carry blood away from the heart (Figure 1, Figure 2, and Figure 3). Veins and venules carry blood to the heart. An exception to this generalization are the portal veins, which carry blood from one organ to another (e.g., the hepatic portal vein, which carries blood from the gut to the liver). Capillaries are the smallest vessels and are the site of exchange of oxygen, nutrients, and waste products between the tissues and the blood. Figure 1 Normal artery within the pancreas in a male F344/N rat from a chronic study. The smooth muscle layer is the thickest layer. 1 Blood Vessel – Introduction Figure 2 Normal tunica media (asterisks) and tunica intima (arrows) of an artery within the pancreas in a male F344/N rat from a chronic study (higher magnification of Figure 1). Arteries and veins have walls composed of three layers: the tunica intima, the tunica media, and the tunica adventitia. The tunica intima is composed of endothelial cells on a basement membrane and a subendothelial layer of collagen and elastic fibers. The tunica media consists of smooth muscle cells, elastic fibers, and collagen. The tunica adventitia is composed of collagen and elastic fibers. The relative amounts of each of these components vary depending on the type of vessel. The tunica intima and tunica media of elastic arteries are generally thicker than those of the other types, and the tunica 2 Blood Vessel – Introduction Figure 3 Normal aorta in a male B6C3F1/N mouse from a chronic study. -

Bronchial-Artery Embolisation Information for Patients This Leaflet Tells You About the Bronchial-Artery Embolisation Procedure
Oxford Centre for Respiratory Medicine Bronchial-Artery Embolisation Information for patients This leaflet tells you about the bronchial-artery embolisation procedure. It explains what is involved and what the possible risks are. It is not meant to replace informed discussion between you and your doctor, but can act as a starting point for such a discussion. Whether you are having a planned bronchial-artery embolisation or an emergency procedure, you should make sure that the procedure has been fully explained to you before you sign the consent form. If you have any questions, please ask the doctor or nurse. page 2 The Radiology Department The Radiology Department may also be called the X-ray or Imaging department. It is the facility in the hospital where we carry out radiological examinations of patients, using a range of X-ray equipment such as a CT (computed tomography) scanner, an ultrasound machine and a MRI (magnetic resonance imaging) scanner. Radiologists are doctors specially trained to interpret (understand) the images produced during these scans and to carry out more complex examinations. They are supported by radiographers who are highly trained to carry out X-rays and other imaging procedures. What is a bronchial-artery embolisation? A bronchial-artery embolisation (BAE) is a procedure where X-rays are used to examine the bronchial arteries (arteries in your lung). This allows the doctor to find the bronchial artery which is bleeding and causing your haemoptysis (coughing up of blood). Blood vessels (veins and arteries) do not show up on a normal chest X-ray. In order to see the bronchial arteries a special dye is injected into the artery, via the groin, through a fine plastic tube called a catheter. -

Arterial Variations of the Subclavian-Axillary Arterial Tree: Its Association with the Supply of the Rotator Cuff Muscles
Int. J. Morphol., 32(4):1436-1443, 2014. Arterial Variations of the Subclavian-Axillary Arterial Tree: Its Association with the Supply of the Rotator Cuff Muscles Variaciones Arteriales del Árbol Arterial Subclavio-Axilar. Su Asociación con la Irrigación del Manguito de los Rotadores N. Naidoo*; L. Lazarus*; B. Z. De Gama*; N. O. Ajayi* & K. S. Satyapal* NAIDOO, N.; LAZARUS, L.; DE GAMA, B. Z.; AJAYI, N. O. & SATYAPAL, K. S. Arterial variations of the subclavian-axillary arterial tree: Its association with the supply of the rotator cuff muscles. Int. J. Morphol., 32(4):1436-1443, 2014. SUMMARY: The subclavian-axillary arterial tree is responsible for the arterial supply to the rotator cuff muscles as well as other shoulder muscles. This study comprised the bilateral dissection of the shoulder and upper arm region in thirty-one adult and nineteen fetal cadaveric specimens. The variable origins and branching patterns of the axillary, subscapular, circumflex scapular, thoracodorsal, posterior circumflex humeral and suprascapular arteries identified in this study corroborated the findings of previous studies. In addition, unique variations that are unreported in the literature were also observed. The precise anatomy of the arterial distribution to the rotator cuff muscles is important to the surgeon and radiologist. It will aid proper interpretation of radiographic images and avoid injury to this area during surgical procedures. KEY WORDS: Subclavian-axillary arterial tree; Variations; Supply; Rotator cuff muscles. INTRODUCTION Standard anatomical textbooks divide the axillary identified by Saralaya et al. (2008) to arise as a large artery into three parts using its relation to the pectoralis minor collateral branch from the first part of the axillary artery muscle (Salopek et al., 2007). -

Journal of Neurology Research Review & Reports
Journal of Neurology Research Review & Reports Case Report Open Access Bilateral Tortuous Upper Limb Arterial Tree and Their Clinical Significance Alka Bhingardeo Department of Anatomy, All India Institute of Medical Sciences, Bibinagar ABSTRACT The detailed knowledge about the possible anatomical variations of upper limb arteries is vital for the reparative surgery of the region. Brachial artery is the main artery of upper limb; it is a continuation of axillary artery from the lower border of teres major muscle. During routine cadaveric dissection, we found bilateral tortuous brachial artery which was superficial as well as tortuous throughout its course. It is called superficial as it was superficial to the median nerve. At the neck of radius, it was divided into two terminal branches radial and ulnar arteries which were also tortuous. Tortuosity of the radial artery was more near the flexor retinaculum. When observed, the continuation of ulnar artery as superficial palmar arch also showed tortuosity throughout, including its branches. Being superficial such brachial artery can be more prone to trauma. Tortuous radial artery is one of the causes of access failure in trans-radial approach of coronary interventions. To the best of our knowledge, this is the first case where entire post axillary upper limb arterial system is tortuous bilaterally. So knowledge of such tortuous upper limb arterial tree is important for cardiologist, radiologist, plastic surgeons and orthopedic surgeons. *Corresponding author Alka Bhingardeo, Assistant Professor, Department of Anatomy, All India Institute of Medical Sciences, Bibinagar, Telangana, India, Mob: 8080096151, Email: [email protected] Received: November 08, 2020; Accepted: November 16, 2020; Published: November 21, 2020 Keywords: Radial Artery, Superficial Brachial Artery, Tortuous, Brachial Artery Ulnar Artery, Upper Limb The brachial artery commenced from the axillary artery at the lower border of teres major muscle. -

The Aorta, and Pulmonary Blood Flow
Br Heart J: first published as 10.1136/hrt.36.5.492 on 1 May 1974. Downloaded from British HeartJournal, I974, 36, 492-498. Relation between fetal flow patterns, coarctation of the aorta, and pulmonary blood flow Elliot A. Shinebourne and A. M. Elseed From the Department of Paediatrics, Brompton Hospital, National Heart and Chest Hospitals, London Intracardiac anomalies cause disturbances in fetal flow patterns which in turn influence dimensions of the great vessels. At birth the aortic isthmus, which receives 25 per cent of the combinedfetal ventricular output, is normally 25 to 30 per cent narrower than the descending aorta. A shelf-like indentation of the posterior aortic wall opposite the ductus characterizes thejunction of the isthmus with descending aorta. In tetralogy ofFallot, pulmonary atresia, and tricuspid atresia, when pulmonary blood flow is reduced from birth, the main pul- monary artery is decreased and ascending aorta increased in size. Conversely in intracardiac anomalies where blood is diverted away from the aorta to the pulmonary artery, isthmal narrowing or the posterior indentation may be exaggerated. Analysis of I62 patients with coarctation of the aorta showed 83 with an intracardiac anomaly resulting in increased pulmonary bloodflow and 21 with left-sided lesions present from birth. In contrast no patients with coarctation were found with diminished pulmonary flow or right-sided obstructive lesions. From this evidence the hypothesis is developed that coarctation is prevented whenflow in the main pulmonary artery is reduced in thefetus. http://heart.bmj.com/ The association of coarctation with left-sided establishing the complete intracardiac diagnosis in I62 obstructive lesions such as mitral and aortic stenosis patients with coarctation.