The Moon Illusion Explained Introduction and Summary
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

12 Retina Gabriele K
299 12 Retina Gabriele K. Lang and Gerhard K. Lang 12.1 Basic Knowledge The retina is the innermost of three successive layers of the globe. It comprises two parts: ❖ A photoreceptive part (pars optica retinae), comprising the first nine of the 10 layers listed below. ❖ A nonreceptive part (pars caeca retinae) forming the epithelium of the cil- iary body and iris. The pars optica retinae merges with the pars ceca retinae at the ora serrata. Embryology: The retina develops from a diverticulum of the forebrain (proen- cephalon). Optic vesicles develop which then invaginate to form a double- walled bowl, the optic cup. The outer wall becomes the pigment epithelium, and the inner wall later differentiates into the nine layers of the retina. The retina remains linked to the forebrain throughout life through a structure known as the retinohypothalamic tract. Thickness of the retina (Fig. 12.1) Layers of the retina: Moving inward along the path of incident light, the individual layers of the retina are as follows (Fig. 12.2): 1. Inner limiting membrane (glial cell fibers separating the retina from the vitreous body). 2. Layer of optic nerve fibers (axons of the third neuron). 3. Layer of ganglion cells (cell nuclei of the multipolar ganglion cells of the third neuron; “data acquisition system”). 4. Inner plexiform layer (synapses between the axons of the second neuron and dendrites of the third neuron). 5. Inner nuclear layer (cell nuclei of the bipolar nerve cells of the second neuron, horizontal cells, and amacrine cells). 6. Outer plexiform layer (synapses between the axons of the first neuron and dendrites of the second neuron). -
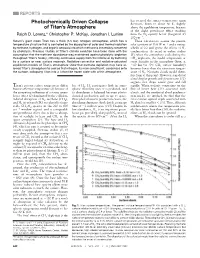
Photochemically Driven Collapse of Titan's Atmosphere
REPORTS has escaped, the surface temperature again Photochemically Driven Collapse decreases, down to about 86 K, slightly of Titan’s Atmosphere above the equilibrium temperature, because of the slight greenhouse effect resulting Ralph D. Lorenz,* Christopher P. McKay, Jonathan I. Lunine from the N2 opacity below (longward of) 200 cm21. Saturn’s giant moon Titan has a thick (1.5 bar) nitrogen atmosphere, which has a These calculations assume the present temperature structure that is controlled by the absorption of solar and thermal radiation solar constant of 15.6 W m22 and a surface by methane, hydrogen, and organic aerosols into which methane is irreversibly converted albedo of 0.2 and ignore the effects of N2 by photolysis. Previous studies of Titan’s climate evolution have been done with the condensation. As noted in earlier studies assumption that the methane abundance was maintained against photolytic depletion (5), when the atmosphere cools during the throughout Titan’s history, either by continuous supply from the interior or by buffering CH4 depletion, the model temperature at by a surface or near surface reservoir. Radiative-convective and radiative-saturated some altitudes in the atmosphere (here, at equilibrium models of Titan’s atmosphere show that methane depletion may have al- ;10 km for 20% CH4 surface humidity) lowed Titan’s atmosphere to cool so that nitrogen, its main constituent, condenses onto becomes lower than the saturation temper- the surface, collapsing Titan into a Triton-like frozen state with a thin atmosphere. -

Pupil Responses Associated with Coloured Afterimages Are Mediated by the Magno-Cellular Pathway
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Aston Publications Explorer Vision Research 43 (2003) 1423–1432 www.elsevier.com/locate/visres Pupil responses associated with coloured afterimages are mediated by the magno-cellular pathway S. Tsujimura *, J.S. Wolffsohn, B. Gilmartin Neurosciences Research Institute, Aston University, Aston Triangle, Birmingham B4 7ET, UK Received 14 August 2002; received in revised form 27 January 2003 Abstract Sustained fixation of a bright coloured stimulus will, on extinction of the stimulus and continued steady fixation, induce an afterimage whose colour is complementary to that of the initial stimulus; an effect thought to be caused by fatigue of cones and/or of cone-opponent processes to different colours. However, to date, very little is known about the specific pathway that causes the coloured afterimage. Using isoluminant coloured stimuli recent studies have shown that pupil constriction is induced by onset and offset of the stimulus, the latter being attributed specifically to the subsequent emergence of the coloured afterimage. The aim of the study was to investigate how the offset pupillary constriction is generated in terms of input signals from discrete functional elements of the magno- and/or parvo-cellular pathways, which are known principally to convey, respectively, luminance and colour signals. Changes in pupil size were monitored continuously by digital analysis of an infra-red image of the pupil while observers viewed isoluminant green pulsed, ramped or luminance masked stimuli presented on a computer monitor. It was found that the amplitude of the offset pupillary constriction decreases when a pulsed stimulus is replaced by a temporally ramped stimulus and is eliminated by a luminance mask. -

PREDICTIVE PROCESSING in the RETINA THROUGH EVALUATION of the OMITTED-STIMULUS RESPONSE by SAMANTHA I. FRADKIN a Thesis to Be Su
PREDICTIVE PROCESSING IN THE RETINA THROUGH EVALUATION OF THE OMITTED-STIMULUS RESPONSE By SAMANTHA I. FRADKIN A thesis to be submitted to the Graduate School-New Brunswick Rutgers, The State University of New Jersey In partial fulfillment of the requirements For the degree of Master of Science Graduate Program in Psychology Written under the direction of Steven M. Silverstein And approved by ______________________________________________ ______________________________________________ ______________________________________________ New Brunswick, New Jersey October 2020 ABSTRACT OF THE THESIS Predictive Processing in the Retina Through Evaluation of the Omitted-Stimulus Response By SAMANTHA I. FRADKIN Thesis Director: Dr. Steven M. Silverstein While previous studies have demonstrated that individuals with schizophrenia demonstrate predictive coding abnormalities in high-level vision, it is unclear whether impairments exist in low-level predictive processing within the disorder. Evaluation of the omitted-stimulus response (OSR), i.e., activity following the omission of a light flash subsequent to a repetitive stimulus, has been examined previously to assess prediction within retinal activity. Given that little research has focused on the OSR in humans, the present study investigated if predictive processing could be detected at the retinal level within a healthy human sample, and whether this activity was associated with high-level predictive processing. Flash electroretinography (fERG) was recorded while eighteen healthy control participants viewed a series of consecutive light flashes within a 1.96 Hz single-flash condition with a flash luminance of 85 Td · s, as well as a 28.3 Hz flicker condition with a flash luminance of 16 Td · s. Participants also completed the Ebbinghaus ii task, a context sensitivity task that assesses high-level predictive processing, and the Audio-Visual Abnormalities Questionnaire (AVAQ), which measures frequency of self- reported auditory and visual sensory distortions. -

Localisation of Visual Hallucinations
BRITISH MEDICAL JOURNAL 16 JULY 1977 147 of hypothermia; the duration of cardiac arrest; and the disturbances of sleep or consciousness.4 Hallucinations may be promptness and correctness of treatment. Peterson's pessi- evoked by sensory deprivation, but other factors are usually mistic report from California,8 in which all 15 near-drowned present; thus the "black-patch" delirium that may follow children who had fits, fixed dilated pupils, flaccidity, and loss cataract extraction in the elderly probably results from sensory Br Med J: first published as 10.1136/bmj.2.6080.147 on 16 July 1977. Downloaded from of pain sensation suffered severe anoxic encephalopathy, deprivation and mild senile brain changes and is more frequent may be explained by the high water temperatures there. In when hearing is also impaired.5 warm water the protective effect of hypothermia against brain Hallucinations may be due to focal lesions. Past experiences, damage would be missing. In contrast was the case described the quality of eidetic imagery, and psychodynamic "actors in Trondheim, Norway,9 in which a 5-year-old fell through influence the content of organic hallucinosis,6 and it would be ice in fresh water with an outside temperature of 10° below unwise to lean too heavily on the occurrence and nature of zero centigrade. He was in the water for 22 minutes and was hallucinosis in localising intracranial lesions. Visual hallucina- brought out apparently dead, with widely dilated pupils and tions are a relatively infrequent accompaniment oflesions ofthe bluish white skin. He was warmed up (the method was not calcarine cortex (Brodmann's area 17), which has few thalamo- described) and-despite the risks noted above-was given cortical connections; yet they may occur as a false-localising external cardiac massage without suffering ventricular symptom of frontal or subtentorial lesions. -

The Roles and Functions of Cutaneous Mechanoreceptors Kenneth O Johnson
455 The roles and functions of cutaneous mechanoreceptors Kenneth O Johnson Combined psychophysical and neurophysiological research has nerve ending that is sensitive to deformation in the resulted in a relatively complete picture of the neural mechanisms nanometer range. The layers function as a series of of tactile perception. The results support the idea that each of the mechanical filters to protect the extremely sensitive recep- four mechanoreceptive afferent systems innervating the hand tor from the very large, low-frequency stresses and strains serves a distinctly different perceptual function, and that tactile of ordinary manual labor. The Ruffini corpuscle, which is perception can be understood as the sum of these functions. located in the connective tissue of the dermis, is a rela- Furthermore, the receptors in each of those systems seem to be tively large spindle shaped structure tied into the local specialized for their assigned perceptual function. collagen matrix. It is, in this way, similar to the Golgi ten- don organ in muscle. Its association with connective tissue Addresses makes it selectively sensitive to skin stretch. Each of these Zanvyl Krieger Mind/Brain Institute, 338 Krieger Hall, receptor types and its role in perception is discussed below. The Johns Hopkins University, 3400 North Charles Street, Baltimore, MD 21218-2689, USA; e-mail: [email protected] During three decades of neurophysiological and combined Current Opinion in Neurobiology 2001, 11:455–461 psychophysical and neurophysiological studies, evidence has accumulated that links each of these afferent types to 0959-4388/01/$ — see front matter © 2001 Elsevier Science Ltd. All rights reserved. a distinctly different perceptual function and, furthermore, that shows that the receptors innervated by these afferents Abbreviations are specialized for their assigned functions. -

Investigation of Tactile Illusion Based on Gestalt Theory
philosophies Article Investigation of Tactile Illusion Based on Gestalt Theory Hiraku Komura 1,* , Toshiki Nakamura 2 and Masahiro Ohka 2 1 Faculty of Engineering, Kyushu Institute of Technology, 1-1 Sensui-cho, Tobata-ku, Kitakyushu-shi 804-8550, Japan 2 Graduate School of Informatics, Nagoya University, Furo-cho, Chikusa-ku, Nagoya 464-8601, Japan; [email protected] (T.N.); [email protected] (M.O.) * Correspondence: [email protected] Abstract: Time-evolving tactile sensations are important in communication between animals as well as humans. In recent years, this research area has been defined as “tactileology,” and various studies have been conducted. This study utilized the tactile Gestalt theory to investigate these sensations. Since humans recognize shapes with their visual sense and melodies with their auditory sense based on the Prägnanz principle in the Gestalt theory, this study assumed that a time-evolving texture sensation is induced by a tactile Gestalt. Therefore, the operation of such a tactile Gestalt was investigated. Two psychophysical experiments were conducted to clarify the operation of a tactile Gestalt using a tactile illusion phenomenon called the velvet hand illusion (VHI). It was confirmed that the VHI is induced in a tactile Gestalt when the laws of closure and common fate are satisfied. Furthermore, it was clarified that the tactile Gestalt could be formulated using the proposed factors, which included the laws of elasticity and translation, and it had the same properties as a visual Gestalt. For example, the strongest Gestalt factor had the highest priority among multiple competing factors. Keywords: tactileology; tactile gestalt; principle of prägnanz; law of closure; formulation; psy- chophysics; velvet hand illusion; dot-matrix display; texture sensation Citation: Komura, H.; Nakamura, T.; Ohka, M. -

Real Time Measurement and Processing of Pupillary Light Reflex for Early Detection of Disease
Journal of Computers Real Time Measurement and Processing of Pupillary Light Reflex for Early Detection of Disease Ippei Torii*, Takahito Niwa Aichi Institute of Technology, Dept. of Information Science, 1247 Yachigusa, Yakusa-cho, Toyota, Aichi, Japan. * Corresponding author. Tel.: 81-565-48-8121; email: mac[aitech.ac.jp Manuscript submitted January 10, 2019; accepted March 8, 2019. doi: 10.17706/jcp.14.3.161-169 Abstract: Recently, pupillary measurements have begun to be considered effective in the diagnosis of various physical conditions. Apart from optic neuropathy and retinal disorders, which are ocular diseases, diversions can be expected in the diagnosis of autonomic disturbance due to sympathetic and parasympathetic nerve disorders, cranial nerve disorders, cerebral infarction, depression, and diabetes. In this study, we have developed a real-time pupil diameter measuring system that is inexpensive and does not require a complicated device. When strong light is projected onto the eyeball, this system can measure the reaction time until the start of miosis, the time to achieve maximal miosis, and the difference in reaction speed of the left and right eyes. With this system, the status of a disease can be judged based on the distance from the threshold value. Key words: Real time measurement, eye movement, early detection of disease, image processing. 1. Introduction There are approximately one hundred million photoreceptor cells in the retina of human eyes. Light that shines on those cells is converted to nerve signals, which transmit the information to the brain, resulting in the visual recognition of objects. When light is radiated onto the eye, the pupillary light reflex is triggered, causing the pupillary diameter to decrease with a time delay of less than 1 sec. -

Eye-Movement Studies of Visual Face Perception
Eye-movement studies of visual face perception Joseph Arizpe A dissertation submitted for the degree of Doctor of Philosophy of the University College London Institute of Cognitive Neuroscience University College London 2015 1 Declaration I, Joseph Arizpe, confirm that the work presented in this thesis is my own. Where information has been derived from other sources, I confirm that this has been indicated in the thesis. 2 Abstract This thesis investigates factors influencing eye-movement patterns during face perception, the relationship of eye-movement patterns to facial recognition performance, and methodological considerations impacting the detection of differences in eye-movement patterns. In particular, in the first study (chapter 2), in which the basis of the other-race effect was investigated, differences in eye- movement patterns during recognition of own- versus other-race (African, Chinese) faces were found for Caucasian participants. However, these eye- movement differences were subtle and analysis-dependent, indicating that the discrepancy in prior reports regarding the presence or absence of such differences are due to variability in statistical sensitivity of analysis methods across studies. The second and third studies (chapters 3 and 4) characterized visuomotor factors, specifically pre-stimulus start position and distance, which strongly influence subsequent eye-movement patterns during face perception. An overall bias in fixation patterns to the opposite side of the face induced by start position and an increasing undershoot of the first ordinal fixation with increasing start distance were found. These visuomotor influences were not specific to faces and did not depend on the predictability of the location of the upcoming stimulus. -

Subliminal Afterimages Via Ocular Delayed Luminescence: Transsaccade Stability of the Visual Perception and Color Illusion
ACTIVITAS NERVOSA SUPERIOR Activitas Nervosa Superior 2012, 54, No. 1-2 REVIEW ARTICLE SUBLIMINAL AFTERIMAGES VIA OCULAR DELAYED LUMINESCENCE: TRANSSACCADE STABILITY OF THE VISUAL PERCEPTION AND COLOR ILLUSION István Bókkon1,2 & Ram L.P. Vimal2 1Doctoral School of Pharmaceutical and Pharmacological Sciences, Semmelweis University, Budapest, Hungary 2Vision Research Institute, Lowell, MA, USA Abstract Here, we suggest the existence and possible roles of evanescent nonconscious afterimages in visual saccades and color illusions during normal vision. These suggested functions of subliminal afterimages are based on our previous papers (i) (Bókkon, Vimal et al. 2011, J. Photochem. Photobiol. B) related to visible light induced ocular delayed bioluminescence as a possible origin of negative afterimage and (ii) Wang, Bókkon et al. (Brain Res. 2011)’s experiments that proved the existence of spontaneous and visible light induced delayed ultraweak photon emission from in vitro freshly isolated rat’s whole eye, lens, vitreous humor and retina. We also argue about the existence of rich detailed, subliminal visual short-term memory across saccades in early retinotopic areas. We conclude that if we want to understand the complex visual processes, mere electrical processes are hardly enough for explanations; for that we have to consider the natural photobiophysical processes as elaborated in this article. Key words: Saccades Nonconscious afterimages Ocular delayed bioluminescence Color illusion 1. INTRODUCTION Previously, we presented a common photobiophysical basis for various visual related phenomena such as discrete retinal noise, retinal phosphenes, as well as negative afterimages. These new concepts have been supported by experiments (Wang, Bókkon et al., 2011). They performed the first experimental proof of spontaneous ultraweak biophoton emission and visible light induced delayed ultraweak photon emission from in vitro freshly isolated rat’s whole eye, lens, vitreous humor, and retina. -

Light, Color, and Atmospheric Optics
Light, Color, and Atmospheric Optics GEOL 1350: Introduction To Meteorology 1 2 • During the scattering process, no energy is gained or lost, and therefore, no temperature changes occur. • Scattering depends on the size of objects, in particular on the ratio of object’s diameter vs wavelength: 1. Rayleigh scattering (D/ < 0.03) 2. Mie scattering (0.03 ≤ D/ < 32) 3. Geometric scattering (D/ ≥ 32) 3 4 • Gas scattering: redirection of radiation by a gas molecule without a net transfer of energy of the molecules • Rayleigh scattering: absorption extinction 4 coefficient s depends on 1/ . • Molecules scatter short (blue) wavelengths preferentially over long (red) wavelengths. • The longer pathway of light through the atmosphere the more shorter wavelengths are scattered. 5 • As sunlight enters the atmosphere, the shorter visible wavelengths of violet, blue and green are scattered more by atmospheric gases than are the longer wavelengths of yellow, orange, and especially red. • The scattered waves of violet, blue, and green strike the eye from all directions. • Because our eyes are more sensitive to blue light, these waves, viewed together, produce the sensation of blue coming from all around us. 6 • Rayleigh Scattering • The selective scattering of blue light by air molecules and very small particles can make distant mountains appear blue. The blue ridge mountains in Virginia. 7 • When small particles, such as fine dust and salt, become suspended in the atmosphere, the color of the sky begins to change from blue to milky white. • These particles are large enough to scatter all wavelengths of visible light fairly evenly in all directions. -

The Moon Illusion and Size–Distance Scaling—Evidence for Shared Neural Patterns
The Moon Illusion and Size–Distance Scaling—Evidence for Shared Neural Patterns Ralph Weidner1*, Thorsten Plewan1,2*, Qi Chen1, Axel Buchner3, Peter H. Weiss1,4, and Gereon R. Fink1,4 Abstract ■ A moon near to the horizon is perceived larger than a moon pathway areas including the lingual and fusiform gyri. The func- at the zenith, although—obviously—the moon does not change tional role of these areas was further explored in a second ex- its size. In this study, the neural mechanisms underlying the periment. Left V3v was found to be involved in integrating “moon illusion” were investigated using a virtual 3-D environ- retinal size and distance information, thus indicating that the ment and fMRI. Illusory perception of an increased moon size brain regions that dynamically integrate retinal size and distance was associated with increased neural activity in ventral visual play a key role in generating the moon illusion. ■ INTRODUCTION psia; Sperandio, Kaderali, Chouinard, Frey, & Goodale, Although the moon does not change its size, the moon 2013; Enright, 1989; Roscoe, 1989). near to the horizon is perceived as relatively larger com- One concept of size constancy scaling implies that the pared with when it is located at the zenith. This phenome- retinal image size and the estimated distance of an object non is called the “moon illusion” and is one of the oldest are conjointly considered, thereby enabling constant size visual illusions known (Ross & Plug, 2002). Despite exten- perception of objects at different distances (Kaufman & sive research, no consensus has been reached regarding Kaufman, 2000). With respect to the moon illusion, appar- the underlying perceptual and neural correlates (Ross & ent distance theories, for example, propose that “the per- Plug, 2002; Hershenson, 1989).