DOCSLIB.ORG

Translation of the Kimberling's Glossary Into

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text

Load more

Translation of the Kimberling’s Glossary into barycentrics (v48-dvipdfm) June 13, 2012 Acknowledgement. This document began its life as a private copy of the Glossary accompanying the Encyclopedia of Clark Kimberling. This Glossary - as its name suggests - is organized alpha- betically. As a –never satisfied– newcomer, I would have preferred a progression from the easiest to the hardest topics and I reordered this document in my own way. It is unclear whether this new ordering will be useful to someone else ! In any case a detailed index is provided. Second point, the Glossary is written using trilinear coordinates. From an advanced point of view, these coordinates are neither better nor worse than the barycentric coordinates. Nevertheless, having some practice of the barycentrics, and none of the trilinears, I undertook to translate everything, from one system to another. In any case, this was a formative exercise, and this also puts the focus on the covariance/contravariance properties that were subsequently systematized. Drawings are the third point. Everybody knows –or should know– that geometry is not possible at all without drawings. Having no intention to pay royalties for using rulers and compasses, I turned to an open source software (kseg) in order to produce my own drawings. Thereafter, I have used Geogebra, together with pstricks. What a battle, but no progress without practice ! Subsequently, other elements have been incorporated from other sources, including materials about cubics, from the Gibert web site. Finally, original elements were also added. As it will appear at first sight, "pldx" is addicted to a tradition that requires a precisely specified universal space for each object to live in. A second massive addiction of the author is computer algebra. Having at your fingertips a tool that gives the right answer to each and every expansion or factorization, and never lost the small paper sheet where the computation of the week was summarized is really great. Moreover, being constrained to explain everything to a computer helps to specify all the required details. For example, the "equivalence up to a proportionality factor" doesn’t apply in the same way to a matrix whether this matrix describes a collineation, a triangle, a trigon or a set of incidence relations. In this document, "beautiful geometrical proofs" are avoided as most as possible, since they are the most error prone. A safe proof of "the triangle of contacts of the inscribed circle and the triangle of the mid-arcs on the circumcircle admit the similicenter of the two circles as perspector (and therefore as center of similitude)" is : ency(persp(matcev(pX(7)),matucev(pX(1)))) 7! 56 where the crucial point is ency, i.e. a safe implementation of the Kimberling’s search key method to explore the database. To summarize, the present document is rather a "derived work", where the elements presented are not intended to be genuine, apart perhaps from the way to assemble the pieces and cook them all together. Index =well known circles, 108 cevadiv, 41, 150 =well known conics, 85 cevadivision, 151 =well known cubics, 166 cevamul, 40, 150 =well known lines, 24 cevapoint, 41 =well known triangles, 33 cevian collineation, 150 cevian conics, 86 A cevian conjugacies, 151 affix (complex), 137 cevian lines, 32 affix (Morley), 139 cevian nest, 38 affix, Morley, 140 cevian triangle, 32 alephdivision, 151 circle, 105 Al-Kashi, 46, 50, 106 circle (list of well known circles), 108 angle between lines, 54 circlekit, 106 anticevian triangle, 34 circum-anticevian, 71 anticomplement, 31, 150 circumcevian, 71 anticomplementary conjugate, 195 circumcircle, 85, 109 anticomplementary triangle, 31, 33 circumconic, 82 antigonal conjugacy, 163 circumconic (circumhyperbola), 95 antimedial triangle, 31 circumconic, asymptote, 95 antiorthic axis, 24 circumhyperbola, 95 Apollonius circle, 112 cK(F,U), 176 Arbelos, 117 cocevian triangle, 34 area (complex formula), 137 collinear, 18 area (Heron), 50 collineation, 147 area (matrix), 50 collineation algorithm, 147 Collings transform, 199 B backward matrix, 140 complement, 31, 150 backward substitutions, 142 complementary conjugate, 195 Barycentric division, 21 complex affix, 137 barycentric multiplication, 21, 149 concurrent, 19 barycentrics, 18, 21 conic, 77 barycentrics (standard), 19 Conic-cross-ratio, 156 base points (pencil of circles), 126, 161 conico-pivotal isocubic, 176 Bevan circle, 112 conjugate circle, 111 Bevan line, 24 cosinus of projection, 58 bicentric points, 27 cross conjugacy, 39 Brocard 3-6 circle, 115 cross ratio of four points, 32 Brocard ellipse, 92 crossdiff, 196 Brocard line, 24 crossdifference, 23 Brocard points, 56 crossdiv, 39, 150 Brocard second circle, 115 crossmul, 38, 150 crosspoint, 39 C cross-ratio, 155 center of a circle, 106 crosssum, 196 center of a conic, 80 crosssumbar, 196 central line, 27 crosssumdiv, 196 central point, 27 crosstriangle, 36 central triangle, 29 cubic, 165 ceva conjugacy, 41 cubic (list of well known cubics), 166 3 4 INDEX cubic (triangular), 168 hyperbola (inhyperbola), 96 cubic cK(F,U), 176 cubic nK(P,U,k), 175 I cubic nK0(P,U), 175 incentral triangle, 33 cubic pK(P,U), 166 incircle, 85, 86, 110 cubics PKA, 168 Incircle transform, 110 cycle, 122 inconic, 83 cyclocevian conjugate, 119 inconic (inhyperbola), 96 cyclopedal conjugate, 60 infinity line, 24 inhyperbola, 96 D intouch triangle, 33 dalethdivision, 153 inverse in a circle, 108 Daneels (first) perspector, 42 involutive collineation, 148 Darboux cubic, 171 isoceles triangles, 117 DC point, 73 Isoconjugacy, 161 de Longchamps axis, 24 isogonal conjugacy, 60 desmic mate, 73 isogonal conjugacy (Morley), 162 distance point-line, 56 isoptic pencil, 126 distance point-point, 51 isotomic conjugacy, 34 dual of a conic, 80 isotomic pencil, 125 Dual triangle, 73 duality, 22 J Jerabek RH, 85 E eigencenter, 154 K eigentransform, 174 K219, 96 embedded vector, 50 K170 cubic, 167, 174, 177 Euler line, 24 K004 Darboux, 171 excentral triangle, 33 K155 EAC2, 173 Exceter point, 71 K007 Lucas, 171 extouch triangle, 33 K003 McKay, 169 K001 Neuberg, 170 F K010 Simson, 177 focus, 88 K002 Thomson, 171 folium, 77 K-ellipse, 92 forward matrix, 140 Kiepert parabola, 85, 143 forward substitutions, 140 Kiepert RH, 85, 117 fourth harmonic, 32, 155 K-matrix, 50 Fuhrmann 4-8 circle, 116 kseg, 20 Fuhrmann triangle, 33, 192 L G Lemoine axis, 24 geogebra, 20 Lemoine first circle, 113 Gergonne axis, 24 Lemoine inconic, 85 Gibert-Simson transform, 177 Lemoine second circle, 114 gimeldivision, 152 limit points (pencil of circles), 125, 161 Gt mapping, 101 line, 18 gudulic point, 88 line (list of well known lines), 24 line at infinity, 19, 141 H Longchamps circle, 112 harmonic division, 32 Lubin parametrization, 140 helethdivision, 153 Lucas cubic, 171 Hirst inverse, 196 hirstpoint, 196 M homoltriangle, 36 MacBeath circumconic, 86 homothecy, 58 MacBeath inconic, 86 horizon, 122 major center, 27 hyperbola, 94 matrix K, 50 hyperbola (circumhyperbola), 95 matrix M, 54, 141 June 13, 2012 14:18 published under the GNU Free Documentation License INDEX 5 matrix OrtO, 53, 141 polynomial center, 27 matrix Pyth, 51, 141 power, 51 matrix W, 49, 141 power formula, 51, 105 McKay cubic K003, 169 projector (orthogonal), 57 medial triangle, 31, 33 psi-Kimberling, 151 Menelaus theorem, 35 Pythagoras theorem, 51 Miguel theorem, 35 Pyth-matrix, 51 mimosa, 152 Morley affix, 139, 140 R Morley space, 138 radical trace, 107 multiplier of an homography, 158 radius of a circle, 106, 125 rational center, 28 N reciprocal conjugacy, 161 Nagel line, 24 rectangular hyperbola, 95 Neuberg circles, 56 reflection, 31 Neuberg K001 cubic, 170 representative, 122 nine points circle, 86 RH, 95 nine-points circle, 111 Rigby point, 65 nK(P,U,k), 175 rotation, 149 nK0(P,U), 175 RS, 65 non pivotal isocubic, 165 S O Saragossa points, 73 orthic axis, 24, 62 search key, Kimberling, 19 orthic triangle, 33 search key, Morley, 20, 142 orthoassociate, 67 Second Daneels perspector, 43 orthocentroidal 2-4 circle, 116 shortest cubic, 170 orthocorrespondent, 67 similitude, 148 orthodir, 54, 141 similitude (centers of), 107 orthogonal projector, 57, 149 Simpson line, 61 orthogonal reflection, 58, 149 Simson cubic, 177 orthojoin, 64 Simson-Moses point, 66 orthologic (triangles), 67 sine-triple-angle circle, 114 Orthopoint, 53 SM, 66 orthopole, 62 Soddy (but not so) circles, 131 OrtO-matrix, 53 Soddy circles, 130 Soddy line, 24 P Sondat, 181 parabola, 81, 93 Spieker circle, 112 pedal triangle, 59 sqrtdiv, 22, 159 Pelle à Tarte, 117 sqrtmul, 22 pencil, 123 squarediv, 42 perspectivity, 36 squaremul, 42 perspectivity with ABC, 37 SR, 65 perspector, 36, 37 Star triangle, 192 perspector of a conic, 81 star triangle, 33 perspectrix, 36, 37 Steinbart transform, 71 pivot of a cubic, 165 Steiner circumellipse, 43, 85 pivotal conic, 176 Steiner inellipse, 85, 90 pivotal umbilical pK, 169 Steiner line, 61 PK transform, 167 symbolic substitution, 29 pK(P,U), 166 symmetrical functions, 140 Plucker formulas, 79 symmetry (orthogonal), 58 point, 18 polar wrt a conic, 80 T polar wrt a curve, 77 tangent, 54 polars-of-points triangle, 153 tangent of two lines, 54, 141 pole wrt a conic, 80 tangent to curve, 77 poles-of-lines triangle, 153 tangential triangle, 33 —– pldx : Translation of the Kimberling’s Glossary into barycentrics —– 6 INDEX Tarry point, 57 TCC-perspector, 71 Tg mapping, 101 Thomson K002 cubic, 171 transcendental center, 27 translation, 148 transpose, 23 triangle, 18 triangle (list of well known triangles), 33 triangle (may be degenerate), 18 triangle center, 27 trigone, 19 trilinear pole (deprecated), 23 Trilinears, 21 tripolar, 23 tripolar centroid, 36 tripolar line, 34 tripole, 23 type-crossing, 20 type-keeping, 20 U umbilics, 122 unary cofactor triangle, 154 V vandermonde, 140 Vertex associate, 74 vertex triangle, 36 vertex trigon, 36 visible point, 139 W wedge operator, 22 W-matrix, 49 Y Yff parabola, 85 Z Z(U) cubic, 168 Z+cubic, 176 zosma, 153 June 13, 2012 14:18 published under the GNU Free Documentation License List of Figures 1.1 Point P and line A”B”C” are the tripolars of each other.
Recommended publications
  • Self-Inverse Gemini Triangles

    Self-Inverse Gemini Triangles

    INTERNATIONAL JOURNAL OF GEOMETRY Vol. 9 (2020), No. 1, 25 - 39 SELF-INVERSE GEMINI TRIANGLES CLARK KIMBERLING and PETER MOSES Abstract. In the plane of a triangle ABC, every triangle center U = u : v : w (barycentric coordinates) is associated with a central triangle having A-vertex AU = −u : v + w : v + w. The triangle AU BU CU is a self-inverse Gemini triangle. Let mU (X) be the image of a point X under the collineation that maps A; B; C; G respectively onto AU ;BU ;CU ;G, where G is the centroid of ABC. Then mU (mU (X)) = X: Properties of the self-inverse mapping mU are presented, with attention to associated conics (e.g., Jerabek, Kiepert, Feuerbach, Nagel, Steiner), as well as cubics of the types pK(Y; Y ) and pK(U ∗ Y; Y ). 1. Introduction The term Gemini triangle, introduced in the Encyclopedia of Triangle Centers (ETC [7], just before X(24537)), applies to certain triangles defined by barycentric coordinates. In keeping with the meaning of gemini, these triangles tend to occur in pairs. Specifically, for a given reference triangle ABC with sidelengths a; b; c, a Germini triangle A0B0C0 is a cen- tral triangle ([6], pp. 53-56) with A-vertex given by (1.1) A0 = f(a; b; c): g(b; c; a): g(b; a; c); where f and g are center functions ([6], p. 46). Because A0B0C0 is a central triangle, the vertices B0 and C0 can be read from (1.1) as B0 = g(c; b; a): f(b; c; a): g(c; a; b) C0 = g(a; b; c): g(a; c; b): f(c; a; b): Now suppose that U = u : v : w is a triangle center, and let 0 −u v + w v + w 1 MU = @ w + u −v w + u A : u + v u + v −w Keywords and phrases Triangle, Gemini triangle, barycentric coordinates, collineation, conic, cubic, circumcircle, Jerabek, Kiepert, Feuerbach, Nagel, Steiner (2010)Mathematics Subject Classification: 51N15, 51N20 Received: 13.10.2019.
  • Orthocorrespondence and Orthopivotal Cubics

    Orthocorrespondence and Orthopivotal Cubics

    Forum Geometricorum b Volume 3 (2003) 1–27. bbb FORUM GEOM ISSN 1534-1178 Orthocorrespondence and Orthopivotal Cubics Bernard Gibert Abstract. We define and study a transformation in the triangle plane called the orthocorrespondence. This transformation leads to the consideration of a fam- ily of circular circumcubics containing the Neuberg cubic and several hitherto unknown ones. 1. The orthocorrespondence Let P be a point in the plane of triangle ABC with barycentric coordinates (u : v : w). The perpendicular lines at P to AP , BP, CP intersect BC, CA, AB respectively at Pa, Pb, Pc, which we call the orthotraces of P . These orthotraces 1 lie on a line LP , which we call the orthotransversal of P . We denote the trilinear ⊥ pole of LP by P , and call it the orthocorrespondent of P . A P P ∗ P ⊥ B C Pa Pc LP H/P Pb Figure 1. The orthotransversal and orthocorrespondent In barycentric coordinates, 2 ⊥ 2 P =(u(−uSA + vSB + wSC )+a vw : ··· : ···), (1) Publication Date: January 21, 2003. Communicating Editor: Paul Yiu. We sincerely thank Edward Brisse, Jean-Pierre Ehrmann, and Paul Yiu for their friendly and valuable helps. 1The homography on the pencil of lines through P which swaps a line and its perpendicular at P is an involution. According to a Desargues theorem, the points are collinear. 2All coordinates in this paper are homogeneous barycentric coordinates. Often for triangle cen- ters, we list only the first coordinate. The remaining two can be easily obtained by cyclically permut- ing a, b, c, and corresponding quantities. Thus, for example, in (1), the second and third coordinates 2 2 are v(−vSB + wSC + uSA)+b wu and w(−wSC + uSA + vSB )+c uv respectively.
  • Cevians, Symmedians, and Excircles Cevian Cevian Triangle & Circle

    Cevians, Symmedians, and Excircles Cevian Cevian Triangle & Circle

    10/5/2011 Cevians, Symmedians, and Excircles MA 341 – Topics in Geometry Lecture 16 Cevian A cevian is a line segment which joins a vertex of a triangle with a point on the opposite side (or its extension). B cevian C A D 05-Oct-2011 MA 341 001 2 Cevian Triangle & Circle • Pick P in the interior of ∆ABC • Draw cevians from each vertex through P to the opposite side • Gives set of three intersecting cevians AA’, BB’, and CC’ with respect to that point. • The triangle ∆A’B’C’ is known as the cevian triangle of ∆ABC with respect to P • Circumcircle of ∆A’B’C’ is known as the evian circle with respect to P. 05-Oct-2011 MA 341 001 3 1 10/5/2011 Cevian circle Cevian triangle 05-Oct-2011 MA 341 001 4 Cevians In ∆ABC examples of cevians are: medians – cevian point = G perpendicular bisectors – cevian point = O angle bisectors – cevian point = I (incenter) altitudes – cevian point = H Ceva’s Theorem deals with concurrence of any set of cevians. 05-Oct-2011 MA 341 001 5 Gergonne Point In ∆ABC find the incircle and points of tangency of incircle with sides of ∆ABC. Known as contact triangle 05-Oct-2011 MA 341 001 6 2 10/5/2011 Gergonne Point These cevians are concurrent! Why? Recall that AE=AF, BD=BF, and CD=CE Ge 05-Oct-2011 MA 341 001 7 Gergonne Point The point is called the Gergonne point, Ge. Ge 05-Oct-2011 MA 341 001 8 Gergonne Point Draw lines parallel to sides of contact triangle through Ge.
  • Control Point Based Representation of Inellipses of Triangles∗

    Control Point Based Representation of Inellipses of Triangles∗

    Annales Mathematicae et Informaticae 40 (2012) pp. 37–46 http://ami.ektf.hu Control point based representation of inellipses of triangles∗ Imre Juhász Department of Descriptive Geometry, University of Miskolc, Hungary [email protected] Submitted April 12, 2012 — Accepted May 20, 2012 Abstract We provide a control point based parametric description of inellipses of triangles, where the control points are the vertices of the triangle themselves. We also show, how to convert remarkable inellipses defined by their Brianchon point to control point based description. Keywords: inellipse, cyclic basis, rational trigonometric curve, Brianchon point MSC: 65D17, 68U07 1. Introduction It is well known from elementary projective geometry that there is a two-parameter family of ellipses that are within a given non-degenerate triangle and touch its three sides. Such ellipses can easily be constructed in the traditional way (by means of ruler and compasses), or their implicit equation can be determined. We provide a method using which one can determine the parametric form of these ellipses in a fairly simple way. Nowadays, in Computer Aided Geometric Design (CAGD) curves are repre- sented mainly in the form n g (u) = j=0 Fj (u) dj δ Fj :[a, b] R, u [a, b] R, dj R , δ 2 P→ ∈ ⊂ ∈ ≥ ∗This research was carried out as a part of the TAMOP-4.2.1.B-10/2/KONV-2010-0001 project with support by the European Union, co-financed by the European Social Fund. 37 38 I. Juhász where dj are called control points and Fj (u) are blending functions. (The most well-known blending functions are Bernstein polynomials and normalized B-spline basis functions, cf.
  • A Geometric Proof of the Siebeck–Marden Theorem Beniamin Bogosel

    A Geometric Proof of the Siebeck–Marden Theorem Beniamin Bogosel

    A Geometric Proof of the Siebeck–Marden Theorem Beniamin Bogosel Abstract. The Siebeck–Marden theorem relates the roots of a third degree polynomial and the roots of its derivative in a geometrical way. A few geometric arguments imply that every inellipse for a triangle is uniquely related to a certain logarithmic potential via its focal points. This fact provides a new direct proof of a general form of the result of Siebeck and Marden. Given three noncollinear points a, b, c ∈ C, we can consider the cubic polynomial P(z) = (z − a)(z − b)(z − c), whose derivative P (z) has two roots f1, f2. The Gauss–Lucas theorem is a well-known result which states that given a polynomial Q with roots z1,...,zn, the roots of its derivative Q are in the convex hull of z1,...,zn. In the simple case where we have only three roots, there is a more precise result. The roots f1, f2 of the derivative polynomial are situated in the interior of the triangle abc and they have an interesting geometric property: f1 and f2 are the focal points of the unique ellipse that is tangent to the sides of the triangle abc at its midpoints. This ellipse is called the Steiner inellipse associated to the triangle abc. In the rest of this note, we use the term inellipse to denote an ellipse situated in a triangle that is tangent to all three of its sides. This geometric connection between the roots of P and the roots of P was first observed by Siebeck (1864) [12] and was reproved by Marden (1945) [8].
  • Circles in Areals

    Circles in Areals

    Circles in areals 23 December 2015 This paper has been accepted for publication in the Mathematical Gazette, and copyright is assigned to the Mathematical Association (UK). This preprint may be read or downloaded, and used for any non-profit making educational or research purpose. Introduction August M¨obiusintroduced the system of barycentric or areal co-ordinates in 1827[1, 2]. The idea is that one may attach weights to points, and that a system of weights determines a centre of mass. Given a triangle ABC, one obtains a co-ordinate system for the plane by placing weights x; y and z at the vertices (with x + y + z = 1) to describe the point which is the centre of mass. The vertices have co-ordinates A = (1; 0; 0), B = (0; 1; 0) and C = (0; 0; 1). By scaling so that triangle ABC has area [ABC] = 1, we can take the co-ordinates of P to be ([P BC]; [PCA]; [P AB]), provided that we take area to be signed. Our convention is that anticlockwise triangles have positive area. Points inside the triangle have strictly positive co-ordinates, and points outside the triangle must have at least one negative co-ordinate (we are allowed negative masses). The equation of a line looks like the equation of a plane in Cartesian co-ordinates, but note that the equation lx + ly + lz = 0 (with l 6= 0) is not satisfied by any point (x; y; z) of the Euclidean plane. We use such equations to describe the line at infinity when doing projective geometry.
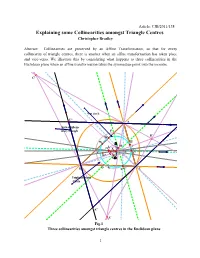
  • Explaining Some Collinearities Amongst Triangle Centres Christopher Bradley

    Explaining Some Collinearities Amongst Triangle Centres Christopher Bradley

    Article: CJB/2011/138 Explaining some Collinearities amongst Triangle Centres Christopher Bradley Abstract: Collinearities are preserved by an Affine Transformation, so that for every collinearity of triangle centres, there is another when an affine transformation has taken place and vice-versa. We illustrate this by considering what happens to three collinearities in the Euclidean plane when an affine transformation takes the symmedian point into the incentre. C' 9 pt circle C'' A B'' Anticompleme ntary triangle F B' W' W E' L M V O X Z E F' K 4 V' K'' Y G T H N' D B U D'U' C Triplicate ratio Circle A'' A' Fig.1 Three collinearities amongst triangle centres in the Euclidean plane 1 1. When the circumconic, the nine-point conic, the triplicate ratio conic and the 7 pt. conic are all circles The condition for this is that the circumconic is a circle and then the tangents at A, B, C form a triangle A'B'C' consisting of the ex-symmedian points A'(– a2, b2, c2) and similarly for B', C' by appropriate change of sign and when this happen AA', BB', CC' are concurrent at the symmedian point K(a2, b2, c2). There are two very well-known collinearities and one less well-known, and we now describe them. First there is the Euler line containing amongst others the circumcentre O with x-co-ordinate a2(b2 + c2 – a2), the centroid G(1, 1, 1), the orthocentre H with x-co-ordinate 1/(b2 + c2 – a2) and T, the nine-point centre which is the midpoint of OH.
  • The Vertex-Midpoint-Centroid Triangles

    The Vertex-Midpoint-Centroid Triangles

    Forum Geometricorum b Volume 4 (2004) 97–109. bbb FORUM GEOM ISSN 1534-1178 The Vertex-Midpoint-Centroid Triangles Zvonko Cerinˇ Abstract. This paper explores six triangles that have a vertex, a midpoint of a side, and the centroid of the base triangle ABC as vertices. They have many in- teresting properties and here we study how they monitor the shape of ABC. Our results show that certain geometric properties of these six triangles are equivalent to ABC being either equilateral or isosceles. Let A, B, C be midpoints of the sides BC, CA, AB of the triangle ABC and − let G be its centroid (i.e., the intersection of medians AA, BB , CC ). Let Ga , + − + − + Ga , Gb , Gb , Gc , Gc be triangles BGA , CGA , CGB , AGB , AGC , BGC (see Figure 1). C − + Gb Ga B A G + − Gb Ga − + Gc Gc ABC Figure 1. Six vertex–midpoint–centroid triangles of ABC. This set of six triangles associated to the triangle ABC is a special case of the cevasix configuration (see [5] and [7]) when the chosen point is the centroid G.It has the following peculiar property (see [1]). Theorem 1. The triangle ABC is equilateral if and only if any three of the trian- = { − + − + − +} gles from the set σG Ga ,Ga ,Gb ,Gb ,Gc ,Gc have the same either perime- ter or inradius. In this paper we wish to show several similar results. The idea is to replace perimeter and inradius with other geometric notions (like k-perimeter and Brocard angle) and to use various central points (like the circumcenter and the orthocenter – see [4]) of these six triangles.
  • Arxiv:2101.02592V1 [Math.HO] 6 Jan 2021 in His Seminal Paper [10]

    Arxiv:2101.02592V1 [Math.HO] 6 Jan 2021 in His Seminal Paper [10]

    International Journal of Computer Discovered Mathematics (IJCDM) ISSN 2367-7775 ©IJCDM Volume 5, 2020, pp. 13{41 Received 6 August 2020. Published on-line 30 September 2020 web: http://www.journal-1.eu/ ©The Author(s) This article is published with open access1. Arrangement of Central Points on the Faces of a Tetrahedron Stanley Rabinowitz 545 Elm St Unit 1, Milford, New Hampshire 03055, USA e-mail: [email protected] web: http://www.StanleyRabinowitz.com/ Abstract. We systematically investigate properties of various triangle centers (such as orthocenter or incenter) located on the four faces of a tetrahedron. For each of six types of tetrahedra, we examine over 100 centers located on the four faces of the tetrahedron. Using a computer, we determine when any of 16 con- ditions occur (such as the four centers being coplanar). A typical result is: The lines from each vertex of a circumscriptible tetrahedron to the Gergonne points of the opposite face are concurrent. Keywords. triangle centers, tetrahedra, computer-discovered mathematics, Eu- clidean geometry. Mathematics Subject Classification (2020). 51M04, 51-08. 1. Introduction Over the centuries, many notable points have been found that are associated with an arbitrary triangle. Familiar examples include: the centroid, the circumcenter, the incenter, and the orthocenter. Of particular interest are those points that Clark Kimberling classifies as \triangle centers". He notes over 100 such points arXiv:2101.02592v1 [math.HO] 6 Jan 2021 in his seminal paper [10]. Given an arbitrary tetrahedron and a choice of triangle center (for example, the circumcenter), we may locate this triangle center in each face of the tetrahedron.
  • An Area Inequality for Ellipses Inscribed in Quadrilaterals

    An Area Inequality for Ellipses Inscribed in Quadrilaterals

    1 Introduction It is well known(see [CH], [K], or [MP]) that there is a unique ellipse in- scribed in a given triangle, T , tangent to the sides of T at their respective midpoints. This is often called the midpoint or Steiner inellipse, and it can be characterized as the inscribed ellipse having maximum area. In addition, one has the following inequality. If E denotes any ellipse inscribed in T , then Area (E) π , (trineq) Area (T ) ≤ 3√3 with equality if and only if E is the midpoint ellipse. In [MP] the authors also discuss a connection between the Steiner ellipse and the orthogonal least squares line for the vertices of T . Definition: The line, £, is called a line of best fit for n given points z1, ..., zn n 2 in C, if £ minimizes d (zj ,l) among all lines l in the plane. Here d (zj,l) j=1 denotes the distance(Euclidean)P from zj to l. In [MP] the authors prove the following results, some of which are also proven in 1 n Theorem A: Suppose zj are points in C,g = zj is the centroid, and n j=1 n n 2 2 2 P Z = (zj g) = zj ng . j=1 − j=1 − (a)P If Z = 0, thenP every line through g is a line of best fit for the points z1, ..., zn. (b) If Z = 0, then the line, £, thru g that is parallel to the vector from 6 (0, 0) to √Z is the unique line of best fit for z1, ..., zn.
  • On a Construction of Hagge

    On a Construction of Hagge

    Forum Geometricorum b Volume 7 (2007) 231–247. b b FORUM GEOM ISSN 1534-1178 On a Construction of Hagge Christopher J. Bradley and Geoff C. Smith Abstract. In 1907 Hagge constructed a circle associated with each cevian point P of triangle ABC. If P is on the circumcircle this circle degenerates to a straight line through the orthocenter which is parallel to the Wallace-Simson line of P . We give a new proof of Hagge’s result by a method based on reflections. We introduce an axis associated with the construction, and (via an areal anal- ysis) a conic which generalizes the nine-point circle. The precise locus of the orthocenter in a Brocard porism is identified by using Hagge’s theorem as a tool. Other natural loci associated with Hagge’s construction are discussed. 1. Introduction One hundred years ago, Karl Hagge wrote an article in Zeitschrift fur¨ Mathema- tischen und Naturwissenschaftliche Unterricht entitled (in loose translation) “The Fuhrmann and Brocard circles as special cases of a general circle construction” [5]. In this paper he managed to find an elegant extension of the Wallace-Simson theorem when the generating point is not on the circumcircle. Instead of creating a line, one makes a circle through seven important points. In 2 we give a new proof of the correctness of Hagge’s construction, extend and appl§ y the idea in various ways. As a tribute to Hagge’s beautiful insight, we present this work as a cente- nary celebration. Note that the name Hagge is also associated with other circles [6], but here we refer only to the construction just described.
  • Coincidence of Centers for Scalene Triangles

    Coincidence of Centers for Scalene Triangles

    Forum Geometricorum b Volume 7 (2007) 137–146. bbb FORUM GEOM ISSN 1534-1178 Coincidence of Centers for Scalene Triangles Sadi Abu-Saymeh and Mowaffaq Hajja Abstract.Acenter function is a function Z that assigns to every triangle T in a Euclidean plane E a point Z(T ) in E in a manner that is symmetric and that respects isometries and dilations. A family F of center functions is said to be complete if for every scalene triangle ABC and every point P in its plane, there is Z∈F such that Z(ABC)=P . It is said to be separating if no two center functions in F coincide for any scalene triangle. In this note, we give simple examples of complete separating families of continuous triangle center functions. Regarding the impression that no two different center functions can coincide on a scalene triangle, we show that for every center function Z and every scalene triangle T , there is another center function Z, of a simple type, such that Z(T )=Z(T ). 1. Introduction Exercise 1 of [33, p. 37] states that if any two of the four classical centers coin- cide for a triangle, then it is equilateral. This can be seen by proving each of the 6 substatements involved, as is done for example in [26, pp. 78–79], and it also follows from more interesting considerations as described in Remark 5 below. The statement is still true if one adds the Gergonne, the Nagel, and the Fermat-Torricelli centers to the list. Here again, one proves each of the relevant 21 substatements; see [15], where variants of these 21 substatements are proved.