Ajuste De Datos Astronomicos Por Medio De Minimos Cuadrados
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Molecular Outflows Identified in the FCRAO CO Survey of the Taurus
Mon. Not. R. Astron. Soc. 000, 000–000 (0000) Printed 10 November 2018 (MN LATEX style file v2.2) Molecular Outflows Identified in the FCRAO CO Survey of the Taurus Molecular Cloud Gopal Narayanan1, Ronald Snell1, and Ashley Bemis1;2 1 Dept. of Astronomy, Univ. of Massachusetts, Amherst MA 01003 2 Department of Physics and Astronomy, Bonn University, Wegelerstrasse 8, 53115 Bonn, Germany Received 2012 June 14; in original form 2012 April 23; accepted 2012 June 22 ABSTRACT Jets and outflows are an integral part of the star formation process. While there are many detailed studies of molecular outflows towards individual star-forming sites, few studies have surveyed an entire star-forming molecular cloud for this phenomenon. The 100 square degree FCRAO CO survey of the Taurus molecular cloud provides an excellent opportunity to under- take an unbiased survey of a large, nearby, molecular cloud complex for molecular outflow activity. Our study provides information on the extent, energetics and frequency of outflows in this region, which are then used to assess the impact of outflows on the parent molecular cloud. The search identified 20 outflows in the Taurus region, 8 of which were previously unknown. Both 12CO and 13CO data cubes from the Taurus molecular map were used, and dynamical properties of the outflows are derived. Even for previously known outflows, our large-scale maps indicate that many of the outflows are much larger than previously suspected, with eight of the flows (40%) being more than a parsec long. The mass, momentum and kinetic energy from the 20 outflows are compared to the repository of turbulent energy in Taurus. -

Organic Molecules and Water in the Inner Disks of T Tauri Stars
Organic Molecules and Water in the Inner Disks of T Tauri Stars John S. Carr Naval Research Laboratory, Code 7211, Washington, DC 20375, USA [email protected] Joan R. Najita National Optical Astronomy Observatory, 950 N. Cherry Avenue, Tucson, AZ 85716, USA [email protected] ABSTRACT We report high signal-to-noise Spitzer IRS spectra of a sample of eleven classical T Tauri stars. Molecular emission from rotational transitions of H2O and OH and ro-vibrational bands of simple organic molecules (CO2, HCN, C2H2) is common among the sources in the sample. The emission shows a range in both flux and line-to-continuum ratio for each molecule and in the flux ratios of different molecular species. The gas temperatures (200–800 K) and emitting areas we derive are consistent with the emission originating in a warm disk atmosphere in the inner planet formation region at radii < 2 AU. The H2O emission appears to form under a limited range of excitation conditions, as demonstrated by the similarity in relative strengths of H2O features from star to star and the narrow range in derived temperature and column density. Emission from highly excited rotational levels of OH is present in all stars; the OH emission flux increases with the stellar accretion rate, and the OH/H2O flux ratio shows a relatively small scatter. We interpret these results as evidence for OH production via FUV photo-dissociation of H2O in the disk surface layers. No obvious explanation is found for the observed range in the relative emission strengths of different organic molecules or in their strength with respect to water. -

Binocular Double Star Logbook
Astronomical League Binocular Double Star Club Logbook 1 Table of Contents Alpha Cassiopeiae 3 14 Canis Minoris Sh 251 (Oph) Psi 1 Piscium* F Hydrae Psi 1 & 2 Draconis* 37 Ceti Iota Cancri* 10 Σ2273 (Dra) Phi Cassiopeiae 27 Hydrae 40 & 41 Draconis* 93 (Rho) & 94 Piscium Tau 1 Hydrae 67 Ophiuchi 17 Chi Ceti 35 & 36 (Zeta) Leonis 39 Draconis 56 Andromedae 4 42 Leonis Minoris Epsilon 1 & 2 Lyrae* (U) 14 Arietis Σ1474 (Hya) Zeta 1 & 2 Lyrae* 59 Andromedae Alpha Ursae Majoris 11 Beta Lyrae* 15 Trianguli Delta Leonis Delta 1 & 2 Lyrae 33 Arietis 83 Leonis Theta Serpentis* 18 19 Tauri Tau Leonis 15 Aquilae 21 & 22 Tauri 5 93 Leonis OΣΣ178 (Aql) Eta Tauri 65 Ursae Majoris 28 Aquilae Phi Tauri 67 Ursae Majoris 12 6 (Alpha) & 8 Vul 62 Tauri 12 Comae Berenices Beta Cygni* Kappa 1 & 2 Tauri 17 Comae Berenices Epsilon Sagittae 19 Theta 1 & 2 Tauri 5 (Kappa) & 6 Draconis 54 Sagittarii 57 Persei 6 32 Camelopardalis* 16 Cygni 88 Tauri Σ1740 (Vir) 57 Aquilae Sigma 1 & 2 Tauri 79 (Zeta) & 80 Ursae Maj* 13 15 Sagittae Tau Tauri 70 Virginis Theta Sagittae 62 Eridani Iota Bootis* O1 (30 & 31) Cyg* 20 Beta Camelopardalis Σ1850 (Boo) 29 Cygni 11 & 12 Camelopardalis 7 Alpha Librae* Alpha 1 & 2 Capricorni* Delta Orionis* Delta Bootis* Beta 1 & 2 Capricorni* 42 & 45 Orionis Mu 1 & 2 Bootis* 14 75 Draconis Theta 2 Orionis* Omega 1 & 2 Scorpii Rho Capricorni Gamma Leporis* Kappa Herculis Omicron Capricorni 21 35 Camelopardalis ?? Nu Scorpii S 752 (Delphinus) 5 Lyncis 8 Nu 1 & 2 Coronae Borealis 48 Cygni Nu Geminorum Rho Ophiuchi 61 Cygni* 20 Geminorum 16 & 17 Draconis* 15 5 (Gamma) & 6 Equulei Zeta Geminorum 36 & 37 Herculis 79 Cygni h 3945 (CMa) Mu 1 & 2 Scorpii Mu Cygni 22 19 Lyncis* Zeta 1 & 2 Scorpii Epsilon Pegasi* Eta Canis Majoris 9 Σ133 (Her) Pi 1 & 2 Pegasi Δ 47 (CMa) 36 Ophiuchi* 33 Pegasi 64 & 65 Geminorum Nu 1 & 2 Draconis* 16 35 Pegasi Knt 4 (Pup) 53 Ophiuchi Delta Cephei* (U) The 28 stars with asterisks are also required for the regular AL Double Star Club. -
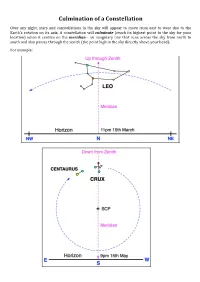
Culmination of a Constellation
Culmination of a Constellation Over any night, stars and constellations in the sky will appear to move from east to west due to the Earth’s rotation on its axis. A constellation will culminate (reach its highest point in the sky for your location) when it centres on the meridian - an imaginary line that runs across the sky from north to south and also passes through the zenith (the point high in the sky directly above your head). For example: When to Observe Constellations The taBle shows the approximate time (AEST) constellations will culminate around the middle (15th day) of each month. Constellations will culminate 2 hours earlier for each successive month. Note: add an hour to the given time when daylight saving time is in effect. The time “12” is midnight. Sunrise/sunset times are rounded off to the nearest half an hour. Sun- Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec Rise 5am 5:30 6am 6am 7am 7am 7am 6:30 6am 5am 4:30 4:30 Set 7pm 6:30 6pm 5:30 5pm 5pm 5pm 5:30 6pm 6pm 6:30 7pm And 5am 3am 1am 11pm 9pm Aqr 5am 3am 1am 11pm 9pm Aql 4am 2am 12 10pm 8pm Ara 4am 2am 12 10pm 8pm Ari 5am 3am 1am 11pm 9pm Aur 10pm 8pm 4am 2am 12 Boo 3am 1am 11pm 9pm 7pm Cnc 1am 11pm 9pm 7pm 3am CVn 3am 1am 11pm 9pm 7pm CMa 11pm 9pm 7pm 3am 1am Cap 5am 3am 1am 11pm 9pm 7pm Car 2am 12 10pm 8pm 6pm Cen 4am 2am 12 10pm 8pm 6pm Cet 4am 2am 12 10pm 8pm Cha 3am 1am 11pm 9pm 7pm Col 10pm 8pm 4am 2am 12 Com 3am 1am 11pm 9pm 7pm CrA 3am 1am 11pm 9pm 7pm CrB 4am 2am 12 10pm 8pm Crv 3am 1am 11pm 9pm 7pm Cru 3am 1am 11pm 9pm 7pm Cyg 5am 3am 1am 11pm 9pm 7pm Del -

Macrocosmo Nº24
A PRIMEIRA REVISTA ELETRÔNICA BRASILEIRA EXCLUSIVA DE ASTRONOMIA macroCOSMO .com ISSN 1808-0731 Ano II - Edição n° 24 - Novembro de 2005 Eclipse Anular 3 de outubro de 2005 O O ^^Q uando a W Lua S o l oculta o w l Cratera de Colônia 25 anos da Aspectos Gerais The Planetary Society revista macroCOSMO .com Ano II - Edição n° 24 - Novembro de 2005 Editorial Redação [email protected] Assim como tantos outros fenômenos naturais, para as primeiras civilizações, os eclipses já foram atribuídos à sinais de múltiplas Diretor Editor Chefe divindades. Eclipses Solares e Lunares, eventos estes repentinos que Hemerson Brandão quebravam a imutabilidade do céu, eram interpretados como [email protected] manifestações de ira dos deuses, predizendo morte de chefes de estado, grandes catástrofes, guerras, e várias pragas. Diagramadores Mesmo nos dias de hoje, com toda a tecnologia e conhecimento Hemerson Brandão adquirido é comum pessoas ficarem receosas com o desaparecimento [email protected] repentino temporário do Sol ou da Lua. Exemplo disso são alguns cristãos Rodolfo Saccani fanáticos, que afirmam que os eclipses são indícios do “fim do mundo”. [email protected] Durante a história, enquanto alguns povos nômades cultivavam um Sharon Camargo temor mítico por esses fenômenos, povos sedentários se empenhavam [email protected] em entender sobre a periodicidade desses fenômenos raros, tentando encontrar padrões que permitissem a previsão dos eclipses. Para isso, Revisão muitos povos erigiram grandes templos e observatórios para estudo e Tasso Napoleão previsão de eclipses além de outros fenômenos celestes. Há quem afirme [email protected] que as pedras megalíticas de Stonehenge, nas ilhas britânicas, estão Walkiria Schulz dispostas numa posição que permitia ao povo que o construiu, prever [email protected] eclipses, há mais de 3700 anos. -

La Constelacion De Tauro
LA CONSTELACION DE TAURO Es una de las constelaciones más interesantes desde el punto de vista observacional entre las que podemos ver desde el hemisferio norte. En la zona de la bóveda celeste donde identificamos la constelación de Tauro encontramos estrellas dobles y dos bellísimos cúmulos abiertos, asi como la famosa Nebulosa del Cangrejo, objeto Messier M1. 1. Las constelaciones: una aparente imágen estelar: Desde nuestra perspectiva visual como habitantes de un pequeño planeta orbitando alrededor de una estrella en una cierta galaxia espiral, observamos, en todas las direcciones de la bóveda celeste, agrupaciones aparentes de estrellas que llamamos constelaciones. Decimos que son agrupaciones aparentes porque, realmente, no tienen que estar - de hecho no lo están en general - agrupadas físicamente. Es esta la misma situación que se nos plantea en nuestra vida cotidiana cuando observamos a lo lejos dos objetos que aparentan estar juntos, y, ante la duda de si lo están o no, nosotros nos movemos lateralmente a una distancia suficiente para observarlos desde una perspectiva lateral. Es en ese momento cuando, vistos desde otro ángulo, comprobamos si están entre sí próximos o no. Este movimiento lateral es muy sencillo de realizar en nuestros avatares de la vida cotidiana, pero es evidente que, a escala astronómica, es imposible con la tecnología existente en nuestra civilización. Es imposible para nosotros salir de la Vía Láctea, nuestra galaxia espiral, para poder observar “lateralmente” una cierta estrella doble, por ejemplo, de la que sospechamos que no es una doble física, interactuando gravitacionalmente, sino que es una doble de perspectiva. Existen métodos radiométricos, espectrométricos, etc.., que nos permiten calcular la distancia de la estrellas que observamos a simple vista, y sabemos que en general, la distancia a nosotros de astros de una misma constelación varía grandemente. -

CURRICULUM VITAE Name: Matthew A. Wood Address
CURRICULUM VITAE Name: Matthew A. Wood Address: Department of Physics and Astronomy Texas A&M University{Commerce Tel: 903-886-5488 Email: [email protected] Education: Ph.D., Astronomy: The University of Texas at Austin, May 1990 M.A., Astronomy: The University of Texas at Austin, Dec. 1985 B.Sci., Physics: Iowa State University, May 1983 Work Experience: 8/12 { Present Deptartment Head & Professor Department of Physics and Astronomy Texas A&M University{Commerce 8/04 { 7/12 Professor Department of Physics & Space Sciences Florida Institute of Technology 8/96 { 7/04 Associate Professor Florida Institute of Technology 6/91 { 7/96 Assistant Professor Florida Institute of Technology 6/90 { 5/91 NSF{NATO Postdoctoral Fellow D´epartement de Physique Universit´ede Montr´eal Societies: American Astronomical Society International Astronomical Union Royal Astronomical Society Sigma Pi Sigma Florida Academy of Sciences Visiting Scientist: International Ultraviolet Explorer Satellite (NASA/Goddard) Kitt Peak National Observatory Mauna Kea Observatory Keck Observatory Hubble Space Telescope McDonald Observatory Proposal Reviewer: NSF / NASA / NOAO / NOVA (Dutch NSF) Referee: The Astrophysical Journal (Main Journal and Letters) Monthly Notices of the Royal Astronomical Society Astronomy and Astrophysics SCIENCE Publications of the Astronomical Society of the Pacific Astrophysics and Space Science Matthew A. Wood Curriculum Vitae Page 2 Major Grants: PI on grants totaling USD $1.9 million. Selected recent: NASA Kepler Mission (PI) \Cataclysmic Variables -

Astronomy with an Opera-Glass
SSSTRONOMY : : Opera-Glass V ASTRONOMY WITH AN OPEEA-GLASS A POPULAE INTRODUCTION TO THE STUDY OF THE STARRY HEAVENS WITH THE SIMPLEST OF OPTICAL INSTRUMENTS WITH MAPS AND DIRECTIONS TO FACILITATE THE RECOGNITION OF THE CONSTELLATIONS AND THE PRINCIPAL STARS VISIBLE TO THE NAKED EYE BY GARRETT P. SERVISS n " Known are their laws ; in harmony unroll The nineteen-orbed cycles of the Moon. And all the signs through which Night whirls her car From belted Orion back to Orion and his dauntless Hound, And all Poseidon's, all high Zeus' stars Bear on their beams true messages to man." Poste's Arattls. EIGHTH EDITION, WITH APPENDIX NEW YOEK D. APPLETON AND COMPANY 72 FIFTH AVENUE LONDON: 33 BEDFORD STREET 1896 Or • \%**- COPYRIGHT, 1888, By D. APPLETON AJSD COMPANY. .. ^ . TO THE READEK. In the pages that follow, the author has endeavored to encourage the study of the heavenly bodies by pointing out some of the interesting and marvelous phenomena of the uni- verse that are visible with little or no assistance from optical instruments, and indicating means of becoming acquainted with the constellations and the planets. Knowing that an opera-glass is capable of revealing some of the most beautiful sights in the starry dome, and believing that many persons would be glad to learn the fact, he set to work with such an instrument and surveyed all the constellations visible in the latitude of New York, carefully noting everything that it seemed might interest amateur star-gazers. All the objects thus observed have not been included in this book, lest the multiplicity of details should deter or discourage the very readers for whom it was specially written. -

Studying Hydrogen Emission Lines from Classical T Tauri Stars: Telluric Line Removal, Physical Conditions in the Emitting Gas, and Reddening
Studying Hydrogen Emission Lines from Classical T Tauri Stars: Telluric Line Removal, Physical Conditions in the Emitting Gas, and Reddening Dissertation zur Erlangung des Doktorgrades des Fachbereichs Physik der Universit¨atHamburg vorgelegt von Natascha Rudolf aus Hamburg Hamburg 2014 ii Gutachter der Dissertation: Prof. Dr. J¨urgenH. M. M. Schmitt Prof. Dr. Ralph Neuh¨auser Gutachter der Disputation: Prof. Dr. Robi Banerjee Dr. Frederic V. Hessman Datum der Disputation: 26. Juni 2014 Vorsitzender des Pr¨ufungsausschusses: Dr. Robert Baade Vorsitzende des Promotionsausschusses: Prof. Dr. Daniela Pfannkuche Dekan der MIN Fakult¨at: Prof. Dr. Heinrich Graener iii Zusammenfassung W¨ahrendihrer Entstehung durchlaufen Sterne verschiedene Entwicklungsphasen, bevor sie die Hauptreihe erreichen. Sie bilden sich durch den gravitativen Kollaps von molekularen Wolken. Die Erhaltung des Drehimpulses erfordert es, dass die Massenakkretion nicht radial, sondern von einer Scheibe aus stattfindet. Sterne mit niedriger Masse, die sich in einer Entwicklungsphase befinden, in der sich das meiste Material in der Scheibe befindet und der Stern nicht mehr in der Wolke verborgen ist, werden klassische T Tauri Sterne (CTTS) genannt. Diese Arbeit befasst sich mit der zirkumstellaren Umgebung dieser Sterne. Die Untersuchungen basieren auf VLT/X-Shooter-Spektren von 20 Sternen mit unterschiedlichen Spektraltypen und Massenakkretionsraten. Die X-Shooter-Spektren decken zeitgleich einen Spektralbereich von etwa 3000 A˚ bis etwa 25 000 A˚ bei einer mittleren Aufl¨osung(R ∼ 10 000) ab. Ein wichtiger Schritt der Datenreduktion ist die Entfernung der tellurischen Linien, die die Erdatmosph¨aredem Spektrum hinzuf¨ugt.An Stelle der Nutzung beobachteter tellurischer Standardsterne verwende ich Modelle der atmosph¨arischen Transmission, die an die Wetterbe- dingungen zum Zeitpunkt der Beobachtung angepasst sind, um diese Kontamination zu entfer- nen. -

Download This Article in PDF Format
A&A 397, 693–710 (2003) Astronomy DOI: 10.1051/0004-6361:20021545 & c ESO 2003 Astrophysics Near-IR echelle spectroscopy of Class I protostars: Mapping Forbidden Emission-Line (FEL) regions in [FeII] C. J. Davis1,E.Whelan2,T.P.Ray2, and A. Chrysostomou3 1 Joint Astronomy Centre, 660 North A’oh¯ok¯u Place, University Park, Hilo, Hawaii 96720, USA 2 Dublin Institute for Advanced Studies, School of Cosmic Physics, 5 Merrion Square, Dublin 2, Ireland 3 Department of Physical Sciences, University of Hertfordshire, Hatfield, Herts AL10 9AB, UK Received 27 August 2002 / Accepted 22 October 2002 Abstract. Near-IR echelle spectra in [FeII] 1.644 µm emission trace Forbidden Emission Line (FEL) regions towards seven Class I HH energy sources (SVS 13, B5-IRS1, IRAS 04239+2436, L1551-IRS5, HH 34-IRS, HH 72-IRS and HH 379-IRS) and three classical T Tauri stars (AS 353A, DG Tau and RW Aur). The parameters of these FEL regions are compared to the characteristics of the Molecular Hydrogen Emission Line (MHEL) regions recently discovered towards the same outflow sources (Davis et al. 2001 – Paper I). The [FeII] and H2 lines both trace emission from the base of a large-scale collimated outflow, although they clearly trace different flow components. We find that the [FeII] is associated with higher-velocity gas than the H2, and that the [FeII] emission peaks further away from the embedded source in each system. This is probably because the [FeII] is more closely associated with HH-type shocks in the inner, on-axis jet regions, while the H2 may be excited along the boundary between the jet and the near-stationary, dense ambient medium that envelopes the protostar. -

Introduction to Basic Stargazing Part III by Michael Usher
Introduction to Basic Stargazing Part III By Michael Usher Before you read this, you need to spend some time out under the stars learning your way around the sky. Now, when you read what I have to say next it will make much better sense. Otherwise you just might say “What is he talking about?” rather than “Oh yeah, I was wondering about that, now I know.” Nevertheless, there is still a great deal of information compressed into a few pages, so don’t feel bad if you have trouble understanding it. Humans took at least 5,000 years to figure all of this out, it’s ok for you to take your time. You can’t spend very much time out under the stars without noticing that everything is moving. Most of the motion is obviously because the earth is rotating. (This was not clear to our ancestors, but that is another subject.) The earth rotates 15 degrees an hour and thus that is the speed the stars move. Notice that the actual velocity the stars move is slower near the pole rather than the celestial equator. The 360 degree circle they need to traverse each day is smaller near the pole than the equator, thus they don’t need to move as quickly. The star gazer can’t help but notice the slow turning of the sky after 15 minutes or so, but there is another additional motion which is which is superimposed on the daily rotational one. If you go out at the same time each night the stars in the east are ever so slightly higher than they were the night before. -

R Alteola Okt R Altqisic Taiyde Tuarasc Il 2013
Ralteolaokt Raltqisic Taiyde Tuarascil 2013 Astronomy and Astrophysics Research Report 2013 Presented to the Governing Board of the School of Cosmic Physics on 28 March 2014 Contents 1 Research Work 1 1.1 High-Energy Phenomena.....................................1 1.1.1 Radiation processes....................................1 1.1.2 High Energy Radiation of Astrophysical sources....................2 1.1.3 HESS related activity....................................5 1.1.4 Electromagnetic Cascades, UHECR, and Neutrinos..................5 1.1.5 High energy emission from binary systems.......................8 1.2 General Theory...........................................9 1.2.1 The problem of small angular scale structure in the cosmic ray anisotropy data.9 1.2.2 Magnetic field generation in shock precursors..................... 10 1.2.3 Analytic Solution for Self-regulated Collective Escape of Cosmic Rays from Their Acceleration Sites...................................... 10 1.3 Star Formation........................................... 11 1.3.1 Characterization of Infrared Dark Clouds: NH3 Observations of an Absorption- contrast Selected IRDC Sample.............................. 11 1.3.2 X-Shooter spectroscopy of young stellar objects: Impact of chromospheric emis- sion on accretion rate estimates............................. 11 1.3.3 An Empirical Correction for Activity Effects on the Temperatures, Radii, and Es- timated Masses of Low-Mass Stars and Brown Dwarfs................ 12 1.3.4 Long-Term Monitoring of Accretion and Outflows in Young Stellar Objects: Search- ing for the Temporal Connection............................. 12 1.3.5 Non-thermal Radio Emission from Young Stellar Object Outflows......... 13 1.3.6 Very Large Array Observations of DG Tau’s Radio Jet: A Highly Collimated Ther- mal Outflow......................................... 13 1.3.7 New brown dwarf discs in Upper Scorpius observed with WISE..........