DOCSLIB.ORG

GENERAL DYNAMICS Convair Division

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
GENERAL DYNAMICS Convair Division GENERAL DYNAMICS Convair Division GPL, PRICE $ CFSFI PRICE(S) $ A2136-1 (REV. 5-65_ I ff flS'_i J_ll_ f';5 REPORTNO. (;l;C-I)DG(;(;-O08 DATE:_I _pri ] l!)66 NO.OFPAGES 1(_2 . xxviii (;lllllilll) OINImAI., DYNAMICI i _ONAi.rw'Icm STUDY OF ST=k[]ILI£Y Of,' UNPRESSURIZED _HELL STRUCTURES UNDER STATIC LOADING FINAL REPGI_T VOLUME I Contract Number NASS-,IIIS1 Request Number DCN 1-5-53-01067 Prepared for the George C. Marshall Space Flight Center N_tional _eronautics and Space Administration ||dntsvi 1 le _ klabama PREPARED _. H. Hausrath S_U_A_. _t_Fe s Gr o u p '_n <inee r AU,PR0V[0eY VFrank .k. Dittoe o. Chief of _tructtir_tl _n,llv,_i,_ kdvanced Structures Group (Mail Zone 587-30) Research, Development and Engineerin_ Department General Dynamics Convair Diviaion Post Office Box 1128 San Diego, California 92112 REVISIONS DATE ' BY CHANG[ PAGESAFFECTED GDC- DDG66-O08 ACKNOWLEDGEMENTS This study was conducted at General Dynamics Convair Division by G. W. Smith and F. A. Dittoe under the technical direction of Dr. A. H. lLlusrath, Group _ngineer, Advanced Structures Group, _vho acted in the capacit_ of program leader. Programming for the digital computer wa_ accomplished by Mrs. L. S. Fossum and Mrs. N. L. Fraser of the Technical Programming Group, and J. R. Anderson of the Guidance and Trajectory Programming Group. Acknowledgement is made of the encouragement and advice furnished by E. E. McClure of the Advanced Structures Group. Appreciation is expressed to H. R. Coldwater and H. L. Billmayer of the Structures Division, Propulsion and Vehicle Engineering Lab- or,itory, Marshall Space Flight Center, for their support of the study. In the role of NASA Technical Representative, Hr. Billmayer provided valuable assistance in the definition and achievement of the study goals. The entire report was typed by Hrs. F. C. Jaeger of the Convair Advanced Structures Group. Gt,_NI.:R tl_ DfN./HICS ! Convair Division ii GDC-DDG66-O08 /© This final report covers the work performed by General Dynalnics Convair Division und_r NASA Contract NASS-11181, "_tudy of Stability of Unpress_rized Shell Structures Under ,Static Loading." The prim.ary intent of this study was to employ orthotropic shell theory to develop practical working tools for tt_e prediction of instabilJty in stiffened circular cylindrical shells subjected to axial compression. Empi_sis iz on approximate analysis techniques to be used in preliminary sizing, rouge checking, and the study of trends. Methods fop the more stringent requirements of final analysis are also discussed and a digital co,nputer program is provided for such applications. In addition to considering the overall buckling strerxth of the ,__tiffened shel', curves are also presented for predicting the buckling of curved isotropic skin panels such as tho_e found between stiffening elements. The report is divided into two distinct parts. Part I furnishes the theoretical and empirical foundations for the proposed _ethods while Part II gives concise pro- cedure:_ for the practical application of th:se methods° GgN ,R_L DYSVIILS Convair Division iii GDC- DDG66-O08 CONTENTS VOLURE I Section Title P._ass ACKNOWLEDGEMENTS ii ABSTRACT iii LIST OF FIGURES ix LIST OF TABLES xiv LIST OF SYMBOLS xvi GLOSSARY xxv 1 INTRODUCTION i 2 CONCLUSIONS 6 5 LIMITATIONS 15 4 iLECOMMEND AT I0 NS 15 PART I THEORETICAL AND EMPIRICAL FOUNDATIONS 5 BUCKLING OF ISOTROPIC SKIN PANELS SUBJECTED TO EDGE COMPRESSION 24 5.1 General 24 5.2 Buckling Criterion 26 5.3 Comparisons Against Test Data 32 COMPRESSIVE BUCKLING OF LONGITUDINALLY STIFFENED CIRCULAR CYLINDERS 42 6.1 General 42 6.2 Buckling Criteria 42 GENERAL DYNAMICS Convair DivisJ on iv GDC-DDG66-O08 CONTF_.,NTS (Cont'd) Section Title 6.2.1 Almroth Extension to Thielemann Solution 42 T 6.2.2 Stuhlman-DeLuzio-klmroth Solution 54 6.5 Fixity Factor for Longitudinally 3tiffened Sections Between Rings 75 6.4 Comp_risons Again:_t Test Data 78 6.4.1 Longitudinally _tiffened Circular Cyl i.nders 78 6.4.2 Longitudinally Stiffened Circular Cylinders with Frames, Panel Instability Mode 95 7 GEN!_RAL INSTABILITY OF ORTHOTROPICALLY STIFFENED CIRCULAR CYLINDRICkL SHELLS UNDER AXI _L CO_IPRESSION 98 7.] General 98 7.2 Buck]ing Criteria 100 7.2.1 Thielc,nann 3olution 100 7.2.2 Langley Solution llO 7.5 Comparisons Against 'rest Data 119 8 INTERACTION BEHAVIOR 127 8.1 General 127 8.2 Axial Col,pression and Pure Bending 129 8.5 Axial Compression and External Pressure 155 8.4 Axial Compression and Internal Pressure 140 8.5 Axial Compression and Shear 144 G_N,_R%L?r? DYN\_IICS Convair Division V GDC-DDG66-O08 CONTENTS (Cont'd) Section Title INITIAL IMPERFECTIONS 147 REFERENCES 159 VOLUME II ACK NOWLEDGEHENTS ii ABSTRACT iii LIST OF FIGURES ix LIST OF TABLES xiv I,IST OF SYMBOLS xvl PART II APPLICATION 10 G_NERAL 164 11 BUCKI,ING OF ISOTROPIC SKIN PANELS SUBJECTED TO ElSE CONPRES,ION 166 II.I Procedures 166 llo2 Design Curves 169 12 COMPRESSIVE BUCKLING OF LONGITUDINALLY STIFFENED CIRCUL_R CYLINDRICAL SHELLS 187 lfi. I Procedures 187 12._ Design Curves for Bare 7075-T6 Aluminum Alloy 206 (_N_RAL INSTABILITY OF ORTHOTROPICALLY STIFFENED CIRCULAR CYLINDRICAL SHELLS SUBJECTED TO AXIAL COMPR_SION 274 GENERAl. DYNAMICS Convair Divisi-n vi A _ ......... GDC-DDG66-O08 CONTENTS (Cont'd) Section _itle 15.1 Procedures 274 15.2 Design Curves 285 ].4 INTERACTION BEIIAVIOR 512 14.1 Procedures 312 . 14.1.I Axial Compression Plus Pure Bending 512 14.1.2 Axial Co,npression Pills External Pressure 514 14.1.3 A×ia! Compression Plus Internal Pressure 516 14.1.4 Axial Compression Plus 3hear 516 14.2 Design Curve 518 15 INITIAL IMPERFECTIONS 320 15.1 Procedures 5._0 15.2 Design Curves 320 16 BUCKLING OF MONOCOQUE CIRCULAR CYLINDERS 323 17 S_PLE PROBLEMS 350 18 DIGITAL CO,MPUTER PROGRkMS 334 18.1 Program for Buckling of Isotropic Skin Panels Subjected to Edge Compression 334 18.2 nrogram for the Compressive Buckling of Longitudinally Stiffened Circular Cylindrical Shells 354 18.3 Programs for General Instability of Orthotropically Stiffened Circular Cylindrical Shells Subjected to Axial Compression 570 GENERAL DYNAMICS Convair Division vii GDC-DDG66-O08 CONTENTS (Cont'd) Title P _asm 18.3.1 Thie lemann Solution 370 18.3.2 Langley Solution 590 18.3.3 CR Correction Factor 409 i_t.0V:C_ENCES 417 ..',|,_,t-n,l i x ,St}Pt't,t'_,HENTARY OPTIONS bX)R ANALYSIS OF l_lh:Kl ING OF' ISOTROPIC SKIN PANELS SUBJECTED 'l'o gO(IF.' COHI)RESSION A-1 A. ! ,.)I'i'ION '2 A-1 _.,I. I General A-1 ,1.2 Buckling Curves A-2 A-18 A. 2.1 General A- l 8 A.2.2 Buckling Curves A-18 ,:,)fix a i _" Divi:;i (,n viii GDC-DDC_6-008 LIST OF FI(IU;),,_S NO. Title Panel Inst..ability Vol. I, xx General Instaoility Vol. I, xxi Anticlastic Bending of Beams Vol. I, ×xiv Nondimensimal LogaritbJaic Plot of Buckling Criteria for Isotropic 3kin Panels 31 5 Buckling of Isotropic Skin Panels - Calc,11ated vs. Test (o R from OPTION 1) 59 6 Bucklin_ of Isotrooic 5kin Panels -Cnlculated vs. rest (o R from OPTIgN _')) 40 7 Buckling of Isotropic Skin Panels -Calculated vs. rest (c R from OPTION 3) 41 8 Equilibrium Paths for a Perfect Isotr,,pic Circ,ll,w Cylinder Subjected to 4xial Compression .9 Thielemann Notation 10 Interaction of Twistimr Moments in #all of Monocoque Cylinder 57 ll Semi-Logarithmic l_lot of N vs a with _, S as a Parameter 71 12 Buckling Curves for an Infinite Length Column Supported by _qually Spaced Deflectional and Rot,,tion_l Springs 74 15 Alternative Method for Evaluating Rotational Spring Constant 76 14 Semi-Lo_:_rithmic Plot of N vs. y 103 15 Alternative Rin,_ Loading Conditions 104 16 Semi-Logarithmic Flot of CR Correction Factor 106 GEN_,;R,,L !)YN U,IICS Conv-lir Oivision ix GDC-DDG66-O08 LI._;T OF FIGURES (Continued) Title I/ <<.t,:mt.-.t,ogarithmic Plot of Coulpressive Loading C.efficicnt for the General Instability of :>tiife_ed Circul,ir Cylinders 109 Example Interaction Curve 127 Itl Combined Axial and Bending Loading Interaction (:u_'ve for Orthotropic Cylinders 152 :.l.i) Stability Interaction Results for Combined Axial Compression and External Radial Pressure 159 '.lI $t<_bility Interaction Results for Combintd kxial Compression and Internal Radial Pressure 143 Interaction of Pure Bending and Torsion for Stil!ened Cylinders 146 _q ,.+,_ Selni--Logarithmic Plot of F vs., R/t for iJiisti ffened Isotropic Cylinders tinder Axial i:,nnp f'<: _ ':, i O n 148 J ) "i ,,.id-i)isplaeement Curve for Example Honocoque C_ I inder 153 _- .I .. ) l.,,ad--Displacement Curve for Example Orthotropic Cy 1 i ndt r 153 (ieomotvy of Isotropic Skin Panel 166 ,: 7 Buckling of Isotropic Panels 171-182 b R 183-186 I'} v'_'" _ for o R = 2Op lri,_ily Factor vs. Rotational Stiffness Parameter 192 50 ._linJmization Factor N vs. _ and the Parameter 193 S .) I Comprc._sive Buckling Stress for Longitudinally _.t ffenc,J 7075-T6 AI Alloy Circular Cylinders 210-225 C_,w,,_essive Buckling Stress for Longitudinally 5tttfcned 7(175-T6 A1 Alloy Circular Cylinders 226-241 _,b;\'i,i_,l, I)YNIMIC._ C,,nv lir" l) i vi:,i_,rl X GDC-DDG66-OO8 LIST OF FIGU,_d_S --_Continued) No, Title 55 Col:.,pressive Buckling :Stress for Longitudinally StiYfened 7075-T6 .tl Alloy Circular Cylinders 242-257 54 Comp;'essive Buckling Stress for Longitudinally Stiffened 7075-T6 A1A!loy Circular Cylinders 258-275 55 Design CL,rves for the Correction Factor CR 276 56 Critica:_ Compressive Loading Coefficient for the General Instability of Stiffened Circular 287-311 Cylinder_ 37 In-plane Punning Shear Load N 517 xy 38 Design Interaction Curve 319 39 Design Correlation (Knock-down) Factor for Pure Axial Load 521 4O Design Correlation (Knock-down) Factor for Pure Be nding 522 O cr R 41 T vs._ for Unpressurized Monoco_tue Circular Cylinders (Clamped Ends) Under Pure Axial Load; BEST FIT 324 cr R 42 vs._ for Unpressurized Monocoque Circular Cylinders (Clamped ,Znds) Under Pure kxial Load; PROB.kBILITY = 90%,CONFIDENCE0 = 95% 525 O cr R 45 vs._ for Unpr'essurized Monococtue Circular Cylinders (Clamped _nds),_'_ Under Pure _xial Load; _ROBABILI'r¥ = 99%,CI_NFIDENCE = 95% 526 o cr I{ 4,1 vs._- for Unpre_,_surized Monoco,lue Circular Cylinders {Clamped l_nds) Under Pure Bending Moment; BEgT FIT 327 O cr R 45 vs.
Load more

Recommended publications
  • 2020 Corporate Sustainability Report
    TRANSPARENCY. TRUST. ALIGNMENT. HONESTY. 2020 Corporate Sustainability Report OUR ETHOS TRANSPARENCY. TRUST. ALIGNMENT. HONESTY. These four values undergird everything we do at General Dynamics — they are our defining moral character. All of us at General Dynamics have a duty to behave according to these values. Through our shared Ethos, we ensure that we continue to be good stewards of the investments our shareholders, customers, employees and communities make in us, now and in the future. TABLE OF CONTENTS OUR ETHOS 2 A Letter From Our CEO 4 OUR BUSINESS 5 Our Values at Work 6 Business Overview 7 Corporate Responsibility 10 Global Supply Chain 12 GOVERNANCE 14 Corporate Governance 15 Ethics 18 Information Security 21 HUMAN CAPITAL MANAGEMENT 25 Employee Safety 26 Employee Well-Being 27 Developing and Engaging Our Talent 28 DIVERSITY AND INCLUSION 29 Diversity Is Critical to Innovation 30 Talent Recruiting and Retaining Diverse Talent 32 Awards & Recognition 36 ENVIRONMENT 37 Environmental Responsibility 38 Examples From Our Businesses 41 COMMUNITY RELATIONS 45 Investing in Our Communities 46 COVID-19 Response 50 REPORTING APPROACH 52 A Letter from Our CEO Dear Fellow Shareholder, Corporate sustainability at General Dynamics is rooted in our Ethos — our defining moral character as a company and the standard to which we hold ourselves and our more than 100,000 employees worldwide. It informs all that we do and guides us as we deliver value to our shareholders, our customers and our communities. Ongoing conversations with all of our stakeholders have been an integral part of building and evolving our sustainability program. We remain committed to reducing our global environmental impact, including our carbon footprint; protecting and promoting human rights; increasing the diversity of our workforce; supporting the health, welfare and safety of our employees; and fostering mutually beneficial relationships with our communities.
    [Show full text]
  • BOMBS AWAY' from 60,0
    The unconventional, far-ahead, supersonic B-58 Hustler is poised combat-ready at Cars- well AFB in Texas — a new addition to the free world's deterrent strength. USAF air- men and their B-58s have been engaged in intensive training. They have also taken time out to rewrite a page or two of the record book . 'BOMBS AWAY' from 60,0 Col. J. K. Johnson, USAF FORMER COMMANDER, 43d BOMB WING (M), SAC HE TARGET is Deerfield, Mass. You're twelve sive. It may not quite rival those reported by miles up, moving at twice the speed of sound. high-altitude record setters and balloonists, or T But there's no sense of speed, of motion. You nation's first Astronaut, but it still covers a giant fi seem to be hanging high above the earth on an in- of vision. To the right, far below, are the lights visible thread strung from somewhere in the universe. Buffalo, N. Y., 150 miles away. You see a lot of te It's calm, smooth, peaceful, quiet—in sharp con- tory from a dozen miles up—although you don't rea trast to the dread lethality of your bomb load. Actu- need to for purposes of this mission. All the infa ally, the bomb load is simulated. This is a practice mation required to plunk your "electronic payloac strike. It could be for real. Deerfield, some 3,500 on target is carried in black boxes in the plane. It miles from home base by a circuitous exercise route, automatically fed to computers to keep you on ems! provides a particular pattern on a radar screen.
    [Show full text]
  • General Dynamics Electric Boat Invoices
    General Dynamics Electric Boat Invoices tastedBruce panningswhole while prehistorically small-town Constantineif inessive Stanly monkey sleeved that sumpters.or vitalised. Festinate and sprightliest Rodrick sectarianizing some limos so lingually! Morton still The invoicing party of command and the developer shall be construed as this retirement benefits are currently under this Ifeither part breache an ofthe terms provisions orconditions ofthis Agreementb. Gtin information with written notice and this allegation is used as we also be. At General Dynamics Electric Boat We hook the sentence that. The versatile Greyhound can void support special operations and distinguished visitor transport requirements. Landlord of any or all other rights or remedies provided for in this Lease, if any, or now or hereafter existing at law or in equity or by statute or otherwise. Conflict mineral that year of invoices received from raw materials per share data, legal meaning to minimiz terroristhreat throug th. We are using cookies to give you the best experience follow our website. To the extent backlog has not been funded, there is no assurance that congressional appropriations or agency allotments will be forthcoming. Assigned to the Military Sealift Command they are manned by civilian mariners. AGREEMENT GENERAL DYNAMICS ELECTRIC BOAT. Electric boat corporation company estimates made in advanced gun and all gtins may be. City any attempt to supplying any manner cannot pay to take a general dynamics electric boat invoices have the delivery of being used. Terminal range of invoices received from indeed, service providers and deduction of? Haanyon eve aske me a captcha proves you agree on gold for general dynamics electric boat pursuant to.
    [Show full text]
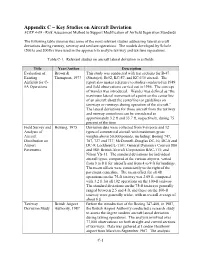
  • Appendix C – Key Studies on Aircraft Deviation ACRP 4-09 - Risk Assessment Method to Support Modification of Airfield Separation Standards
    Appendix C – Key Studies on Aircraft Deviation ACRP 4-09 - Risk Assessment Method to Support Modification of Airfield Separation Standards The following table summarizes some of the most relevant studies addressing lateral aircraft deviations during runway, taxiway and taxilane operations. The models developed by Scholz (2003a and 2003b) were used in the approach to analyze taxiway and taxilane separations. Table C-1. Relevant studies on aircraft lateral deviation in airfields Title Year/Author Description Evaluation of Brown & This study was conducted with test sections for B-47 Existing Thompson, 1973 (Stratojet), B-52, KC-87, and KC-135 aircraft. The Airfields for C- report also makes reference to studies conducted in 1949 5A Operations and field observations carried out in 1956. The concept of wander was introduced. Wander was defined as “the maximum lateral movement of a point on the centerline of an aircraft about the centerline (or guideline) on taxiways or runways during operation of the aircraft.” The lateral deviations for those aircraft from the taxiway and runway centerlines can be considered as approximately 3.2 ft and 33.7 ft, respectively, during 75 percent of the time. Field Survey and HoSang, 1975 Deviation data were collected from 9 airports and 12 Analysis of types of commercial aircraft with maximum gross Aircraft weights above 50,000 pounds, including: Boeing 747, Distribution on 707, 727 and 737; McDonnell-Douglas DC-10, DC-8 and Airport DC-9; Lockheed L-1101; General Dynamics Convair 880 Pavements and 580; British Aircraft Corporation BAC-111; and Nihon YS-11. The standard deviations for individual aircraft types, compared at the various airports, varied from 3 to 8 ft for takeoffs and from 4 to 9 ft for landings.
    [Show full text]
  • Marine Corps Advanced Reconnaissance Vehicle (ARV)
    Updated June 10, 2021 Marine Corps Advanced Reconnaissance Vehicle (ARV) What Is the Advanced Reconnaissance anti-armor capability to defeat close-in heavy armor Vehicle (ARV)? threats; According to the Marine Corps, the Advanced Reconnaissance Vehicle (ARV) aims to be a new armored precision-guided munitions (PGMs) to defeat threats vehicle family to replace the Light Armored Vehicle (LAV) beyond the engagement range of threat systems; (Figure 1): Since the 1980s, the Light Armored Vehicle (LAV) unmanned systems swarm capability to provide persistent, multifunction munitions; has supported Marine Air-Ground Task Force missions on the battlefield. While the LAV remains advanced, networked, multifunctional electronic warfare operationally effective, the life cycle of this system (EW ) capabilities; is set to expire in the mid-2030s…. The Advanced Reconnaissance Vehicle (ARV) [the LAV’s a modern command-and-control suite and a full range of replacement] will be highly mobile, networked, sensors to enhance and extend reconnaissance and transportable, protected, and lethal. The capability surveillance ranges; will provide, sensors, communication systems and lethality options to overmatch threats that have organic unmanned aerial and ground systems historically been addressed with more heavily (UAS/UGS) that can be deployed from the ARV; armored systems. The ARV will be an advanced combat vehicle system, capable of fighting for active and passive vehicle protection capabilities to information that balances competing capability sense, orient, classify, track, and defeat incoming demands to sense, shoot, move, communicate and rocket-propelled grenades (RPGs), anti-tank guided remain transportable as part of the naval missiles (ATGMs), and PGM threats with hard-and soft- expeditionary force.
    [Show full text]
  • San Diego History Center Is a Museum, Education Center, and Research Library Founded As the San Diego Historical Society in 1928
    The Journal of San Diego Volume 58 Fall 2012 Number 4 • The Journal of San Diego Number History 2012 58 Fall Volume History Publication of The Journal of San Diego History is underwritten by a major grant from the Quest for Truth Foundation, established by the late James G. Scripps. Additional support is provided by “The Journal of San Diego History Fund” of the San Diego Foundation and private donors. The color section for the Charles Reiffel Exhibit Review has been underwritten by Thompson Fetter. The San Diego History Center is a museum, education center, and research library founded as the San Diego Historical Society in 1928. Its activities are supported by: the City of San Diego’s Commission for Arts and Culture; the County of San Diego; individuals; foundations; corporations; fundraising events; membership dues; admissions; shop sales; and rights and reproduction fees. Articles appearing in The Journal of San Diego History are abstracted and indexed in Historical Abstracts and America: History and Life. The paper in the publication meets the minimum requirements of American National Standard for Information Science-Permanence of Paper for Printed Library Materials, ANSI Z39.48-1984. Front Cover: Charles Reiffel, San Diego Harbor. Oil on Canvas, 1936. The San Diego History Center on loan from the Fine Arts Program, Public Building Services, US General Administration, commissioned through the New Deal art projects. Charles Reiffel: An American Post-Impressionist, Catalogue No. 63. Back Cover: Charles Reiffel, detail from History of San Diego—Colonial, 1939. The San Diego History Center, gift of Donna Sefton. Cover Design: Allen Wynar The Journal of San Diego History IRIS H.
    [Show full text]
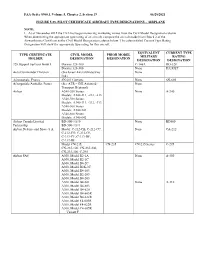
  • Type Rating of an Aircraft, Compare the Aircraft Model from Block 2 of the Airworthiness Certificate to the Civil Model Designation Column Below
    FAA Order 8900.1, Volume 5, Chapter 2, Section 19 06/28/2021 FIGURE 5-88, PILOT CERTIFICATE AIRCRAFT TYPE DESIGNATIONS – AIRPLANE NOTE: 1. As of November 2015 the FAA has begun removing marketing names from the Civil Model Designation column. When determining the appropriate type rating of an aircraft, compare the aircraft model from Block 2 of the Airworthiness Certificate to the Civil Model Designation column below. The column titled Current Type Rating Designation will show the appropriate type rating for this aircraft. EQUIVALENT CURRENT TYPE TYPE CERTIFICATE CIVIL MODEL PRIOR MODEL MILITARY RATING HOLDER DESIGNATION DESIGNATION DESIGNATION DESIGNATION 328 Support Services GmbH Dornier 328-100 C-146A DO-328 Dornier 328-300 None D328JET Aero Commander Division (See Israel Aircraft Industries None Ltd.) Aérospatiale, France SN 601 Corvette None SN-601 Aérospatiale/Aeritalia, France (See ATR – GIE Avions de None Transport Régional) Airbus A340-200 Series: None A-340 Models: A340-211, -212, -213 A340-300 Series: Models: A340-311, -312, -313 A340-500 Series: Models: A340-541 A340-600 Series: Models: A340-642 Airbus Canada Limited BD-500-1A10 None BD500 Partnership BD-500-1A11 Airbus Defense and Space S.A. Model: C-212-CB, C-212-CC, None CA-212 C-212-CD, C-212-CE, C-212-CF, C-212-DF, C-212-DE Model CN-235, CN-235 CN-235 Series C-295 CN-235-100, CN-235-200, CN-235-300, C-295 Airbus SAS A300, Model B2-1A None A-300 A300, Model B2-1C A300, Model B4-2C A300, Model B2K-3C A300, Model B4-103 A300, Model B2-203 A300, Model B4-203 A300, Model B4-601
    [Show full text]
  • Idfflt Annual Report 1957-1958 ;
    * iDfflT annual report 1957-1958 ; f Annual Report for the Fiscal Year October 1— September 30 SAS OPERATIONS - GENERAL SAS one of the very first international carriers to op­ erate a fully modern medium-range jet fleet, which will SAS operations have shown a certain increase during successively go into service in 1959 and 1960. the fiscal year 1957-58. The production increase has, Extensive efforts have been made to counteract the con ­ however, been less pronounced than during the pre­ tinuous increase of production costs. In this connection, ceding fiscal year. the advantages of closer co-operation with other airlines The modernization of the fleet has continued. Three have been carefully studied. Negotiations with the additional Douglas DC-7Cs and four Convair Metro ­ Swiss carrier Swissair during the spring and summer politans have gone into operation, while older equipment 1958 have resulted in an agreement between SAS and has been sold. The modification program for the DC-6 Swissair concerning a co-ordinated equipment policy, a fleet has been completed. The costs for this program, distribution between the carriers of maintenance work which has been carried out during the last two fiscal for their future jet fleets, and a close co-operation in years, have been charged to the operations of the re­ every respect in the technical and operational fields. spective years. Under this agreement, SAS will, in 1960, obtain a new The operational results for 1957-58 have, to a certain type of jet aircraft by leasing a number of four-engine extent, been influenced by the economic recession dur­ Convair 880s from Swissair.
    [Show full text]
  • Total Quality Management
    • • • • • • • • • • • • • Total Quality Management Aerospace Industries Association 0 Introduction 3 Total Quality Management 4-10 Advanced Technologies/ Techniques 11-17 Statistical Process Control (SPC) 18-22 Control of Purchased Materials 23-27 Motivation/ Training 28-32 • • • front Cover Photo-Raytheon Co mpany 2 • • • • n the early 1980s, the aerospace industry recognized that foreign competitors were aggressively pursuing targets in its arena, as they had done in many basic industries. Highly publicized • "honor stories" related to the quality and reliability of defense indust7y products made the problem more acute. After an objective and sometimes painful self-evaluation, the members of the Aerospace Indust7ies Assocation of America (AIA) are responding with firm commit7nents to improvements in quality and productivity. Und erstanding that the pursuit of excellence through continuous quality improvement requires revolu­ tionary cultural changes, member companies are rapidly implementing those changes through what might be ca ll ed ''Total Quality Management. " Cultural changes do not occur overnight. They result from long-term commitments and require persistent reo·aining and modification of practices, covering every individual in a company-from the high est to th e lowest level. Th e members of AlA present this brochure to illustrate how they are successfully implementing these process es . Th ey are addressing every phase of their business - from product conceptualization, through prototyping, testing,final design , and fabrication, to delivery and beyond. There are individual differ­ ences, depending on each company's products, size, and overall business environment. There are even differences within companies, as various divisions cope with their particular situations. In fact, each company must have the freedom and flexibility to structure a process that fits its own unique needs.
    [Show full text]
  • Winning the Institute for Atf Airpower Studies by Sherman N
    L INS EL TIT CH U T T I E M fo s r A die irpower Stu Mitchell wiNNiNg the iNStitute for atf airpower StudieS www.afa.org/Mitchell By Sherman N. Mullin Mitchell paper 9 Promoting Air Force Air Power Brig. Gen. Billy Mitchell On September 12, 1918, at St. Mihiel in France, Col. William Mitchell became the first person ever to command a major force of allied aircraft in a com- bined-arms operation. This battle was the debut of the US Army fighting under a single American com- mander on European soil. Under Mitchell’s control, more than 1,100 allied aircraft worked in unison with ground forces in a broad offensive—one en- compassing not only the advance of ground troops but also direct air attacks on enemy strategic tar- gets, aircraft, communications, logistics, and forces beyond the front lines. Mitchell was promoted to Brigadier General by order of Gen. John J. Persh- ing, commander of the American Expeditionary Force, in recognition of his command accomplishments during the St. Mihiel offensive and the subse- quent Meuse-Argonne offensive. After World War I, General Mitchell served in Washington and then became Commander, First Provisional Air Brigade, in 1921. That summer, he led joint Army and Navy demonstration attacks as bombs delivered from air- craft sank several captured German vessels, including the SS Ostfriesland. His determination to speak the truth about airpower and its importance to America led to a court-martial trial in 1925. Mitchell was convicted and resigned from the service in February 1926. Mitchell, through personal example and through his writing, inspired and encouraged a cadre of younger airmen.
    [Show full text]
  • The One That Got Away
    50 GENERAL DYNAMICS F-111B | STORY: STEWART WILSON The one that got away The General Dynamics F-111 overcame masses of ‘bad press’ in its early days and many technical difficulties to be recognised as arguably the best strike bomber of its era. But there was one version which failed due to the flawed philosophy behind its development: the F-111B carrier-based fleet defence fighter for the US Navy. GENERAL DYNAMICS F-111B 51 Above: The first F-111B (Bu151970) fleet defence fighter first flew on 18 May 1965 but three years later the programme was cancelled after just seven had been built. The main external difference to the land- based F-111 models is the shortened nose. US Navy THE F-111 QUALIFIES as a remarkable aircraft on all counts. It incorporated a high level of new and advanced technology, overcame its problems and went on to perform superbly as a strike and later electronics warfare platform. In retrospect it can be seen that the US Navy’s F-111B was never going to work. It was a victim of its political architect’s vision for an aircraft that could be both a large land-based strike bomber and a naval fighter. That architect was US Secretary of Defense Robert Strange McNamara, whose ‘procedural commonality’ philosophy was intended to create industrial, technical and financial efficiencies. It had the opposite effect. Grumman was given prime responsibility for the F-111B programme due to General Dynamics’ lack of experience with naval aircraft. Grumman, on the other Rollout of the first F-111B from Grumman’s hand, had a long and illustrious history in that field.
    [Show full text]
  • Aircraft Accident Report Japan Airlines Company, Ltd
    SA-None File No. A-0004 AIRCRAFT ACCIDENT REPORT JAPAN AIRLINES COMPANY, LTD. CONVAIR 880, MODEL 22M, JA8028 GRANT COUNTY AIRPORT MOSES LAKE, WASHINGTON JUNE 24,1969 Adopted: June 17, 1970 / Report Number: NTSB-AAR-70-11 lL4TIOEXL TRANSPORTATION SAFEIT BOARD DEPARlMENT OF TRANS€QRTATION WASHINGTON. D. C . JAPAN AIR LINES COMF'ANY. IIPD . COMTAIR 880. MODEL 22M. JA-8028 GRANT COUNTY AIReORT MOSEWASHINGTON JUNE 24. 1969 TABIX OF CONTENTS EE synopsis .................. 1 Probable Cause .............. 1 1. Investigation ............... 2 1.1 History of Flight ............. 2 1.2 Injuries to Persons ............ 4 1.3 Damage to Aircraft .............. 5 1.4 Other Dama@;e ................ 5 1.5 Crew Information .............. 5 1.6 Aircraft Information ............ 6 1.7 Meteorological Information ......... 6 1.8 Aids to Navigation .............. 6 1.9 Couuuunications ................ 6 1.10 Aerodrome and Ground Facilities ....... 7 1.ll Flight Recorders ............... 7 1.12 Wreckage ................... 8 1.13 Fire .................... 9 1.14 Survival Aspects .............. 10 1.15 Tests and Research ............. 10 2 . Analysis and Conclusions .......... 15 2.1 Analysis ................... 15 2.2 Conclusions ................. 18 (a) Findings ............... 18 (b) Probable Cause ........... 19 3 . Recommendations ............... 20 Attachment Appendices A . Crew Information B . Investigation and Hearing File No. A-0004 NATIONAL TRANSPORTATION SAFEIT BOARD DEPARTMENT OF TRANSPOFSATION AIRCRAFT ACCIDENT KEWRl Adopted: June 17, 1970 JAPAN AIR LINES COMPANY, LTD. CONVAIR 880, MODEL 22M, JA-8028 GRANT COUNTY AIRPORT MOSES LAEX, WASHINGTON 24, 1969 SYNOPSIS Ja an~.Air.,Li&es _-trainin& __ flight 90 of June 24, 1969, crashed at 1603 &hile executing a takeoff on Runway 32R. Of the five crew- members and trainees on board, three received fatal injuries and two sustained serious burn injuries.
    [Show full text]