Lesson 19: the Remainder Theorem
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Three Methods of Finding Remainder on the Operation of Modular
Zin Mar Win, Khin Mar Cho; International Journal of Advance Research and Development (Volume 5, Issue 5) Available online at: www.ijarnd.com Three methods of finding remainder on the operation of modular exponentiation by using calculator 1Zin Mar Win, 2Khin Mar Cho 1University of Computer Studies, Myitkyina, Myanmar 2University of Computer Studies, Pyay, Myanmar ABSTRACT The primary purpose of this paper is that the contents of the paper were to become a learning aid for the learners. Learning aids enhance one's learning abilities and help to increase one's learning potential. They may include books, diagram, computer, recordings, notes, strategies, or any other appropriate items. In this paper we would review the types of modulo operations and represent the knowledge which we have been known with the easiest ways. The modulo operation is finding of the remainder when dividing. The modulus operator abbreviated “mod” or “%” in many programming languages is useful in a variety of circumstances. It is commonly used to take a randomly generated number and reduce that number to a random number on a smaller range, and it can also quickly tell us if one number is a factor of another. If we wanted to know if a number was odd or even, we could use modulus to quickly tell us by asking for the remainder of the number when divided by 2. Modular exponentiation is a type of exponentiation performed over a modulus. The operation of modular exponentiation calculates the remainder c when an integer b rose to the eth power, bᵉ, is divided by a positive integer m such as c = be mod m [1]. -

1.3 Division of Polynomials; Remainder and Factor Theorems
1-32 CHAPTER 1. POLYNOMIAL AND RATIONAL FUNCTIONS 1.3 Division of Polynomials; Remainder and Factor Theorems Objectives • Perform long division of polynomials • Perform synthetic division of polynomials • Apply remainder and factor theorems In previous courses, you may have learned how to factor polynomials using various techniques. Many of these techniques apply only to special kinds of polynomial expressions. For example, the the previous two sections of this chapter dealt only with polynomials that could easily be factored to find the zeros and x-intercepts. In order to be able to find zeros and x-intercepts of polynomials which cannot readily be factored, we first introduce long division of polynomials. We will then use the long division algorithm to make a general statement about factors of a polynomial. Long division of polynomials Long division of polynomials is similar to long division of numbers. When divid- ing polynomials, we obtain a quotient and a remainder. Just as with numbers, if a remainder is 0, then the divisor is a factor of the dividend. Example 1 Determining Factors by Division Divide to determine whether x − 1 is a factor of x2 − 3x +2. Solution Here x2 − 3x +2is the dividend and x − 1 is the divisor. Step 1 Set up the division as follows: divisor → x − 1 x2−3x+2 ← dividend Step 2 Divide the leading term of the dividend (x2) by the leading term of the divisor (x). The result (x)is the first term of the quotient, as illustrated below. x ← first term of quotient x − 1 x2 −3x+2 1.3. -

Grade 7/8 Math Circles Modular Arithmetic the Modulus Operator
Faculty of Mathematics Centre for Education in Waterloo, Ontario N2L 3G1 Mathematics and Computing Grade 7/8 Math Circles April 3, 2014 Modular Arithmetic The Modulus Operator The modulo operator has symbol \mod", is written as A mod N, and is read \A modulo N" or "A mod N". • A is our - what is being divided (just like in division) • N is our (the plural is ) When we divide two numbers A and N, we get a quotient and a remainder. • When we ask for A ÷ N, we look for the quotient of the division. • When we ask for A mod N, we are looking for the remainder of the division. • The remainder A mod N is always an integer between 0 and N − 1 (inclusive) Examples 1. 0 mod 4 = 0 since 0 ÷ 4 = 0 remainder 0 2. 1 mod 4 = 1 since 1 ÷ 4 = 0 remainder 1 3. 2 mod 4 = 2 since 2 ÷ 4 = 0 remainder 2 4. 3 mod 4 = 3 since 3 ÷ 4 = 0 remainder 3 5. 4 mod 4 = since 4 ÷ 4 = 1 remainder 6. 5 mod 4 = since 5 ÷ 4 = 1 remainder 7. 6 mod 4 = since 6 ÷ 4 = 1 remainder 8. 15 mod 4 = since 15 ÷ 4 = 3 remainder 9.* −15 mod 4 = since −15 ÷ 4 = −4 remainder Using a Calculator For really large numbers and/or moduli, sometimes we can use calculators to quickly find A mod N. This method only works if A ≥ 0. Example: Find 373 mod 6 1. Divide 373 by 6 ! 2. Round the number you got above down to the nearest integer ! 3. -

Basic Math Quick Reference Ebook
This file is distributed FREE OF CHARGE by the publisher Quick Reference Handbooks and the author. Quick Reference eBOOK Click on The math facts listed in this eBook are explained with Contents or Examples, Notes, Tips, & Illustrations Index in the in the left Basic Math Quick Reference Handbook. panel ISBN: 978-0-615-27390-7 to locate a topic. Peter J. Mitas Quick Reference Handbooks Facts from the Basic Math Quick Reference Handbook Contents Click a CHAPTER TITLE to jump to a page in the Contents: Whole Numbers Probability and Statistics Fractions Geometry and Measurement Decimal Numbers Positive and Negative Numbers Universal Number Concepts Algebra Ratios, Proportions, and Percents … then click a LINE IN THE CONTENTS to jump to a topic. Whole Numbers 7 Natural Numbers and Whole Numbers ............................ 7 Digits and Numerals ........................................................ 7 Place Value Notation ....................................................... 7 Rounding a Whole Number ............................................. 8 Operations and Operators ............................................... 8 Adding Whole Numbers................................................... 9 Subtracting Whole Numbers .......................................... 10 Multiplying Whole Numbers ........................................... 11 Dividing Whole Numbers ............................................... 12 Divisibility Rules ............................................................ 13 Multiples of a Whole Number ....................................... -

Faster Chinese Remaindering Joris Van Der Hoeven
Faster Chinese remaindering Joris van der Hoeven To cite this version: Joris van der Hoeven. Faster Chinese remaindering. 2016. hal-01403810 HAL Id: hal-01403810 https://hal.archives-ouvertes.fr/hal-01403810 Preprint submitted on 27 Nov 2016 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Faster Chinese remaindering Joris van der Hoeven Laboratoire d'informatique, UMR 7161 CNRS Campus de l'École polytechnique 1, rue Honoré d'Estienne d'Orves Bâtiment Alan Turing, CS35003 91120 Palaiseau November 27, 2016 The Chinese remainder theorem is a key tool for the design of ecient multi-modular algorithms. In this paper, we study the case when the moduli m1; :::; m` are xed and can even be chosen by the user. Through an appropriate use of the technique of FFT-trading, we will show that this assumption allows for the gain of an asymptotic factor O(log log `) in the complexity of Chinese remaindering. For small `, we will also show how to choose gentle moduli that allow for further gains at the other end. The multiplication of integer matrices is one typical application where we expect practical gains for various common matrix dimensions and integer bitsizes. -

Understanding the Remainder When Dividing by Fractions Nancy Dwyer University of Detroit Mercy
Understanding the Remainder When Dividing by Fractions Nancy Dwyer University of Detroit Mercy Abstract: Whole number division is extensively modeled to help children intuitively make sense of the remainder as a fractional part of the divisor. To conceptualize division by fractions, children also need extensive modeling of these problems em- bedded in real-world context. Instruction should explicitly combine the paper-and- pencil algorithm with the three models of area measurement, dimensional analysis, and repeated subtraction. In this way, teachers can better help children connect their understanding of the remainder when dividing by fractions to their understanding of remainder in whole number division. Understanding the Remainder When Dividing By Fractions Given a division problem with whole numbers, most students can easily describe what the remainder means. However, when given a division problem in which the divisor is a fraction or mixed number, attaching meaning to the remainder is not so easy. In fact, many children (and adults) who correctly perform the paper-and-pencil calculation, will incorrectly describe what the remainder means. Embedding division by fractions and mixed numbers into real-world measurement problems can be very helpful to learners who are struggling to make sense of these calculations. Example 1: 23÷7 = 3, remainder 2 Children who have developed a part-whole concept of division, when asked what the remainder means, will reply that there are 2 “things” left over. Or, they will say that 2 the remainder 2 means that each person will receive 3 wholes and of whatever you are 7 dividing up and they will tend to name the things as cookies, cakes, etc. -

Efficient Modular Exponentiation
Efficient Modular Exponentiation R. C. Daileda February 27, 2018 1 Repeated Squaring Consider the problem of finding the remainder when am is divided by n, where m and n are both is \large." If we assume that (a; n) = 1, Euler's theorem allows us to reduce m modulo '(n). But this still leaves us with some (potential) problems: 1. '(n) will still be large as well, so the reduced exponent as well as the order of a modulo n might be too big to handle by previous techniques (e.g. with a hand calculator). 2. Without knowledge of the prime factorization of n, '(n) can be very hard to compute for large n. 3. If (a; n) > 1, Euler's theorem doesn't apply so we can't necessarily reduce the exponent in any obvious way. Here we describe a procedure for finding the remainder when am is divided by n that is extremely efficient in all situations. First we provide a bit of motivation. Begin by expressing m in binary1: N X j m = bj2 ; bj 2 f0; 1g and bN = 1: j=0 Notice that N N m PN b 2j Y b 2j Y 2j b a = a j=0 j = a j = (a ) j j=0 j=0 and that 2 2 j j−1 2 j−2 2 2 a2 = a2 = a2 = ··· = a22 ··· : | {z } j squares So we can compute am by repeatedly squaring a and then multiplying together the powers for which bj = 1. If we perform these operations pairwise, reducing modulo n at each stage, we will never need to perform modular arithmetic with a number larger than n2, no matter how large m is! We make this procedure explicit in the algorithm described below. -
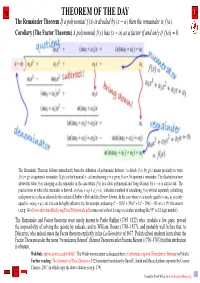
The Remainder Theorem If a Polynomial F (X) Is Divided by (X − Α) Then the Remainder Is F (Α)
THEOREM OF THE DAY The Remainder Theorem If a polynomial f (x) is divided by (x − α) then the remainder is f (α). Corollary (The Factor Theorem) A polynomial f (x) has (x − α) as a factor if and only if f (α) = 0. The Remainder Theorem follows immediately from the definition of polynomial division: to divide f (x) by g(x) means precisely to write f (x) = g(x) × quotient + remainder. If g(x) is the binomial x − a then choosing x = α gives f (a) = 0 × quotient + remainder. The illustration above shows the value f (α) emerging as the remainder in the case where f (x) is a cubic polynomial and ‘long division’ by x − α is carried out. The precise form in which the remainder is derived, α(α(αa0 + a1) + a2) + a3, indicates a method of calculating f (α) without separately calculating each power of α; this iseffectively the content of Ruffini’s Rule and the Horner Scheme. In the case where a1 is nearly equal to −αa0; a2 is nearly 6 5 4 2 equal to −α(αa0 + a1), etc, this can be highly effective; try, for example, evaluating x − 103x + 396x + 3x − 296x − 101 at x = 99: the answer (see p. 14 of www.theoremoftheday.org/Docs/Polynomials.pdf) comes out without having to calculate anything like 996 (a 12-digit number). The Remainder and Factor theorems were surely known to Paolo Ruffini (1765–1822) who, modulo a few gaps, proved the impossibility of solving the quintic by radicals, and to William Horner (1786–1837); and probably well before that, to Descartes,´ who indeed states the Factor theorem explicitly in his La G´eom´etrie of 1637. -

Programming with Numbers and Strings 2
,,. 26 Chapter 1 Introduction CHAPTER I � 2 4. In secondary storage, typically a hard disk. 21. Is the number of minutes at most 300? I 5. The central processing unit. a. If so, the answer is $29.95 x 1.125 = $33.70. PROGRAMMING 6. (1) It would be very tedious to do so. b. If not, (2) Programs that are written for one CPU are 1. Compute the difference: (number of WITH NUMBERS not portable to a different CPU type. minutes)- 300. 7. Ease of use and portability. 2. Multiply that difference by 0.45. 8. The answer varies among systems. A typical 3. Add $29.95. AND STRINGS answer might be /home/dave/csl/hel lo/hello. py 4. Multiply the total by 1.125. That is the or c:\Users\Dave\Workspace\hello\hello. py answer. 9. You back up your files and folders. 22. No. The step If it is more attractive than the "best © samxmeg/iStockphoto. 1 O. Change World to your name (here, Dave): so far" is not executable because there is no objective way f deciding which of two photos print("Hello, Dave!") ? is more attractive. To define and use variables and constants 11. print("H") 23. Pick the first photo and call it "the most expensive so far". print("e") To understand the properties and limitations of integers and floating-point numbers print("l ") For each photo in the sequence print("l ") If it is more expensive than "the most expensive so far" To appreciate the importance of comments and good code layout print("o") Discard "the most expensive so far". -

Basic Python Programming by Examples
LTAM-FELJC [email protected] 1 Basic Python by examples 1. Python installation On Linux systems, Python 2.x is already installed. To download Python for Windows and OSx, and for documentation see http://python.org/ It might be a good idea to install the Enthought distribution Canopy that contains already the very useful modules Numpy, Scipy and Matplotlib: https://www.enthought.com/downloads/ 2. Python 2.x or Python 3.x ? The current version is 3.x Some libraries may not yet be available for version 3, and Linux Ubuntu comes with 2.x as a standard. Many approvements from 3 have been back ported to 2.7. The main differences for basic programming are in the print and input functions. We will use Python 2.x in this tutorial. 3. Python interactive: using Python as a calculator Start Python (or IDLE, the Python IDE). A prompt is showing up: >>> Display version: >>>help() Welcome to Python 2.7! This is the online help utility. ... help> Help commands: modules: available modules keywords: list of reserved Python keywords quit: leave help To get help on a keyword, just enter it's name in help. LTAM-FELJC [email protected] 2 Simple calculations in Python >>> 3.14*5 15.700000000000001 Supported operators: Operator Example Explication +, - add, substract, *, / multiply, divide % modulo 25 % 5 = 0 25/5 = 5, remainder = 0 84 % 5 = 4 84/5 = 16, remainder = 4 ** exponent 2**10 = 1024 // floor division 84//5 = 16 84/5 = 16, remainder = 4 Take care in Python 2.x if you divide two numbers: Isn't this strange: >>> 35/6 5 Obviously the result is wrong! But: >>> 35.0/6 5.833333333333333 >>> 35/6.0 5.833333333333333 In the first example, 35 and 6 are interpreted as integer numbers, so integer division is used and the result is an integer. -

Division of Whole Numbers
The Improving Mathematics Education in Schools (TIMES) Project NUMBER AND ALGEBRA Module 10 DIVISION OF WHOLE NUMBERS A guide for teachers - Years 4–7 June 2011 4YEARS 7 Polynomials (Number and Algebra: Module 10) For teachers of Primary and Secondary Mathematics 510 Cover design, Layout design and Typesetting by Claire Ho The Improving Mathematics Education in Schools (TIMES) Project 2009‑2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations. The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations. © The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE‑EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution‑ NonCommercial‑NoDerivs 3.0 Unported License. 2011. http://creativecommons.org/licenses/by‑nc‑nd/3.0/ The Improving Mathematics Education in Schools (TIMES) Project NUMBER AND ALGEBRA Module 10 DIVISION OF WHOLE NUMBERS A guide for teachers - Years 4–7 June 2011 Peter Brown Michael Evans David Hunt Janine McIntosh Bill Pender Jacqui Ramagge 4YEARS 7 {4} A guide for teachers DIVISION OF WHOLE NUMBERS ASSUMED KNOWLEDGE • An understanding of the Hindu‑Arabic notation and place value as applied to whole numbers (see the module Using place value to write numbers). • An understanding of, and fluency with, forwards and backwards skip‑counting. • An understanding of, and fluency with, addition, subtraction and multiplication, including the use of algorithms. -

Massachusetts Mathematics Curriculum Framework — 2017
Massachusetts Curriculum MATHEMATICS Framework – 2017 Grades Pre-Kindergarten to 12 i This document was prepared by the Massachusetts Department of Elementary and Secondary Education Board of Elementary and Secondary Education Members Mr. Paul Sagan, Chair, Cambridge Mr. Michael Moriarty, Holyoke Mr. James Morton, Vice Chair, Boston Dr. Pendred Noyce, Boston Ms. Katherine Craven, Brookline Mr. James Peyser, Secretary of Education, Milton Dr. Edward Doherty, Hyde Park Ms. Mary Ann Stewart, Lexington Dr. Roland Fryer, Cambridge Mr. Nathan Moore, Chair, Student Advisory Council, Ms. Margaret McKenna, Boston Scituate Mitchell D. Chester, Ed.D., Commissioner and Secretary to the Board The Massachusetts Department of Elementary and Secondary Education, an affirmative action employer, is committed to ensuring that all of its programs and facilities are accessible to all members of the public. We do not discriminate on the basis of age, color, disability, national origin, race, religion, sex, or sexual orientation. Inquiries regarding the Department’s compliance with Title IX and other civil rights laws may be directed to the Human Resources Director, 75 Pleasant St., Malden, MA, 02148, 781-338-6105. © 2017 Massachusetts Department of Elementary and Secondary Education. Permission is hereby granted to copy any or all parts of this document for non-commercial educational purposes. Please credit the “Massachusetts Department of Elementary and Secondary Education.” Massachusetts Department of Elementary and Secondary Education 75 Pleasant Street, Malden, MA 02148-4906 Phone 781-338-3000 TTY: N.E.T. Relay 800-439-2370 www.doe.mass.edu Massachusetts Department of Elementary and Secondary Education 75 Pleasant Street, Malden, Massachusetts 02148-4906 Dear Colleagues, I am pleased to present to you the Massachusetts Curriculum Framework for Mathematics adopted by the Board of Elementary and Secondary Education in March 2017.