Bayesian Analysis of Dyadic Data Arising in Basketball
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Georgia Tech in the 2001 Ncaa Tournament 2000-01 Georgia
GEORGIA TECH IN THE THE YELLOW JACKETS 2001 NCAA TOURNAMENT IN SAN DIEGO NCAA West First & Second Rounds ¥ San Diego, Calif. Facility Thursday, March 15 & Saturday, March 17 Cox Arena 5500 Canyon Crest Drive PRACTICE/PRESS CONFERENCE, Wednesday, March 14 San Diego, CA 92182 All Times Local (Pacific Standard) Phone: 619-594-0234 Georgia Tech Press Conference, 1:30-2:00 p.m. Georgia Tech Practice, 2:10-3:00 p.m. Team Hotel: Town and Country Resort FIRST ROUND PAIRINGS, Thursday, March 15 500 Hotel Circle North All Times Local (Pacific Standard) San Diego, CA 92108 #8 Georgia Tech (17-12) vs. #9 St. Joseph’s (25-6), 11:42 a.m. Phone: 619-297-6006 #1 Stanford (28-2) vs. #16 UNC Greensboro (19-11), 30 min. following Fax: 619-294-5957 #4 Indiana (21-12) vs. #13 Kent State (23-9), 4:55 p.m. #5 Cincinnati (23-9) vs. #12 Brigham Young (23-8), 25 min. following SID: Mike Stamus cell: 404-218-9723 SECOND ROUND, Saturday, March 17 [email protected] All Times Local (Pacific Standard) Assoc. SID: Allison George Cincinnati-Brigham Young winner vs. Indiana-Kent State winner, cell: 678-595-7728 2:38 p.m. [email protected] Stanford-UNC Greensboro winner vs. Georgia Tech-St. Joseph’s winner, 30 min. following Media Hotel: San Diego Marriott Mission Valley 2000-01 GEORGIA TECH ROSTER 8757 Rio San Diego Drive No. Name Pos. Ht. Wt. Cl. Hometown (High School/College) San Diego, CA 92108 2 Darryl LaBarrie G 6-3 196 Sr.-R Decatur, Ga. -

O Klahoma City
MEDIA GUIDE O M A A H C L I K T Y O T R H U N D E 2 0 1 4 2 0 1 5 THUNDER.NBA.COM TABLE OF CONTENTS GENERAL INFORMATION ALL-TIME RECORDS General Information .....................................................................................4 Year-By-Year Record ..............................................................................116 All-Time Coaching Records .....................................................................117 THUNDER OWNERSHIP GROUP Opening Night ..........................................................................................118 Clayton I. Bennett ........................................................................................6 All-Time Opening-Night Starting Lineups ................................................119 2014-2015 OKLAHOMA CITY THUNDER SEASON SCHEDULE Board of Directors ........................................................................................7 High-Low Scoring Games/Win-Loss Streaks ..........................................120 All-Time Winning-Losing Streaks/Win-Loss Margins ...............................121 All times Central and subject to change. All home games at Chesapeake Energy Arena. PLAYERS Overtime Results .....................................................................................122 Photo Roster ..............................................................................................10 Team Records .........................................................................................124 Roster ........................................................................................................11 -
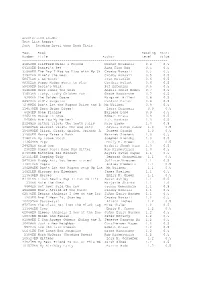
Quizinfo Level
Accelerated Reader Test List Report Sort – Reading Level then Book Title Test Book Reading Point Number Title Author Level Value -------------------------------------------------------------------------- 41850EN Clifford Makes a Friend Norman Bridwell 0.4 0.5 64100EN Daniel's Pet Alma Flor Ada 0.5 0.5 35988EN The Day I Had to Play with My Si Crosby Bonsall 0.5 0.5 31542EN Mine's the Best Crosby Bonsall 0.5 0.5 58671EN I Am Water Jean Marzollo 0.6 0.5 88312EN Puppy Mudge Wants to Play Cynthia Rylant 0.6 0.5 59439EN Rosie's Walk Pat Hutchins 0.6 0.5 31610EN Here Comes the Snow Angela Shelf Medea 0.7 0.5 31613EN Itchy, Itchy Chicken Pox Grace Maccarone 0.7 0.5 9366EN The Golden Goose Margaret Hillert 0.8 0.5 84920EN Sid's Surprise Candace Carter 0.8 0.5 72788EN Don't Let the Pigeon Drive the B Mo Willems 0.9 0.5 114579EN Dora Helps Diego! Laura Driscoll 0.9 0.5 6494EN Gone Fishing Earlene Long 0.9 0.5 44651EN Mouse in Love Robert Kraus 0.9 0.5 5456EN Are You My Mother? P.D. Eastman 1.0 0.5 21245EN Arthur Tricks the Tooth Fairy Marc Brown 1.0 0.5 106265EN Biscuit Visits the Big City Alyssa Satin Capuc 1.0 0.5 104090EN Click, Clack, Splish, Splash: A Doreen Cronin 1.0 0.5 31600EN Harry Takes a Bath Harriet Ziefert 1.0 0.5 31601EN My Loose Tooth Stephen Krensky 1.0 0.5 113649EN Pigs Emily K. -

Set Info - Player - National Treasures Basketball
Set Info - Player - National Treasures Basketball Player Total # Total # Total # Total # Total # Autos + Cards Base Autos Memorabilia Memorabilia Luka Doncic 1112 0 145 630 337 Joe Dumars 1101 0 460 441 200 Grant Hill 1030 0 560 220 250 Nikola Jokic 998 154 420 236 188 Elie Okobo 982 0 140 630 212 Karl-Anthony Towns 980 154 0 752 74 Marvin Bagley III 977 0 10 630 337 Kevin Knox 977 0 10 630 337 Deandre Ayton 977 0 10 630 337 Trae Young 977 0 10 630 337 Collin Sexton 967 0 0 630 337 Anthony Davis 892 154 112 626 0 Damian Lillard 885 154 186 471 74 Dominique Wilkins 856 0 230 550 76 Jaren Jackson Jr. 847 0 5 630 212 Toni Kukoc 847 0 420 235 192 Kyrie Irving 846 154 146 472 74 Jalen Brunson 842 0 0 630 212 Landry Shamet 842 0 0 630 212 Shai Gilgeous- 842 0 0 630 212 Alexander Mikal Bridges 842 0 0 630 212 Wendell Carter Jr. 842 0 0 630 212 Hamidou Diallo 842 0 0 630 212 Kevin Huerter 842 0 0 630 212 Omari Spellman 842 0 0 630 212 Donte DiVincenzo 842 0 0 630 212 Lonnie Walker IV 842 0 0 630 212 Josh Okogie 842 0 0 630 212 Mo Bamba 842 0 0 630 212 Chandler Hutchison 842 0 0 630 212 Jerome Robinson 842 0 0 630 212 Michael Porter Jr. 842 0 0 630 212 Troy Brown Jr. 842 0 0 630 212 Joel Embiid 826 154 0 596 76 Grayson Allen 826 0 0 614 212 LaMarcus Aldridge 825 154 0 471 200 LeBron James 816 154 0 662 0 Andrew Wiggins 795 154 140 376 125 Giannis 789 154 90 472 73 Antetokounmpo Kevin Durant 784 154 122 478 30 Ben Simmons 781 154 0 627 0 Jason Kidd 776 0 370 330 76 Robert Parish 767 0 140 552 75 Player Total # Total # Total # Total # Total # Autos -

Records All-Time Pistons Team Records All-Time Pistons Team Records
RECORDS ALL-TIME PISTONS TEAM RECORDS ALL-TIME PISTONS TEAM RECORDS SINGLE SEASON SINGLE GAME OR PORTION (CONTINUED) Most Points 9,725 1967-68 Steals 877 1976-77 MOST THREE-POINT FIELD GOALS ATTEMPTED Highest Scoring Average 118.6 1967-68 Blocked Shots 572 1982-83 LEADERSHIP Lowest Defensive Average 84.3 2003-04 Most Turnovers 1,858 1977-78 Game 47 at Memphis Apr. 8, 2018 Field Goals 3,840 1984-85 Fewest Turnovers *931 2005-06 Half 28 vs. Atlanta (2nd) Jan. 9, 2015 Field Goals Attempted 8,502 1965-66 Most Victories 64 2005-06 Quarter 15 vs. Atlanta (4th) Jan. 9, 2015 Field Goal % .494 1988-89 Fewest Victories 16 1979-80 MOST REBOUNDS Free Throws 2,408 1960-61 Best Winning % .780 (64-18) 2005-06 Game 107 vs. Boston (at New York) (OT) Nov. 15, 1960 Free Throws Attempted 3,220 1960-61 Poorest Winning % .195 (16-66) 1979-80 Half 52 vs. Seattle (2nd) Jan. 19, 1968 Free Throw % .788 1984-85 Most Home Victories 37 (of 41) 1988-89; 2005-06 Quarter 38 vs. St. Louis (at Olympia) (2nd) Dec. 7, 1960 Three-Point Field Goals 993 2018-19 Fewest Home Victories 9 (of 30) 1963-64 Three-Point Field Goals Attempted 2,854 2018-19 Most Road Victories 27 (of 41) 2005-06; 2006-07 MOST OFFENSIVE REBOUNDS 3-Point Field Goal % .404 1995-96 Fewest Road Victories 3 (of 19) 1960-61 Game 36 at L.A. Lakers Dec. 14, 1975 Most Rebounds 5,823 1961-62 3 (of 38) 1979-80 Half 19 vs. -

2019-20 Panini Flawless Basketball Checklist
2019-20 Flawless Basketball Player Card Totals 281 Players with Cards; Hits = Auto+Auto Relic+Relic Only **Totals do not include 2018/19 Extra Autographs TOTAL TOTAL Auto Relic Block Team Auto HITS CARDS Relic Only Chain A.C. Green 177 177 177 Aaron Gordon 141 141 141 Aaron Holiday 112 112 112 Admiral Schofield 77 77 77 Adrian Dantley 115 115 59 56 Al Horford 385 386 177 169 39 1 Alex English 177 177 177 Allan Houston 236 236 236 Allen Iverson 332 387 295 1 36 55 Allonzo Trier 286 286 118 168 Alonzo Mourning 60 60 60 Alvan Adams 177 177 177 Andre Drummond 90 90 90 Andrea Bargnani 177 177 177 Andrew Wiggins 484 485 118 225 141 1 Anfernee Hardaway 9 9 9 Anthony Davis 453 610 118 284 51 157 Arvydas Sabonis 59 59 59 Avery Bradley 118 118 118 B.J. Armstrong 177 177 177 Bam Adebayo 92 92 92 Ben Simmons 103 132 103 29 Bill Bradley 9 9 9 Bill Russell 186 213 177 9 27 Bill Walton 59 59 59 Blake Griffin 90 90 90 Bob McAdoo 177 177 177 Bobby Portis 118 118 118 Bogdan Bogdanovic 230 230 118 112 Bojan Bogdanovic 90 90 90 GroupBreakChecklists.com 2019-20 Flawless Basketball Player Card Totals TOTAL TOTAL Auto Relic Block Team Auto HITS CARDS Relic Only Chain Bradley Beal 93 95 93 2 Brandon Clarke 324 434 59 226 39 110 Brandon Ingram 39 39 39 Brook Lopez 286 286 118 168 Buddy Hield 90 90 90 Calvin Murphy 236 236 236 Cam Reddish 380 537 59 228 93 157 Cameron Johnson 290 291 225 65 1 Carmelo Anthony 39 39 39 Caron Butler 1 2 1 1 Charles Barkley 493 657 236 170 87 164 Charles Oakley 177 177 177 Chauncey Billups 177 177 177 Chris Bosh 1 2 1 1 Chris Kaman -

Open Andrew Bryant SHC Thesis.Pdf
THE PENNSYLVANIA STATE UNIVERSITY SCHREYER HONORS COLLEGE DEPARTMENT OF ECONOMICS REVISITING THE SUPERSTAR EXTERNALITY: LEBRON’S ‘DECISION’ AND THE EFFECT OF HOME MARKET SIZE ON EXTERNAL VALUE ANDREW DAVID BRYANT SPRING 2013 A thesis submitted in partial fulfillment of the requirements for baccalaureate degrees in Mathematics and Economics with honors in Economics Reviewed and approved* by the following: Edward Coulson Professor of Economics Thesis Supervisor David Shapiro Professor of Economics Honors Adviser * Signatures are on file in the Schreyer Honors College. i ABSTRACT The movement of superstar players in the National Basketball Association from small- market teams to big-market teams has become a prominent issue. This was evident during the recent lockout, which resulted in new league policies designed to hinder this flow of talent. The most notable example of this superstar migration was LeBron James’ move from the Cleveland Cavaliers to the Miami Heat. There has been much discussion about the impact on the two franchises directly involved in this transaction. However, the indirect impact on the other 28 teams in the league has not been discussed much. This paper attempts to examine this impact by analyzing the effect that home market size has on the superstar externality that Hausman & Leonard discovered in their 1997 paper. A road attendance model is constructed for the 2008-09 to 2011-12 seasons to compare LeBron’s “superstar effect” in Cleveland versus his effect in Miami. An increase of almost 15 percent was discovered in the LeBron superstar variable, suggesting that the move to a bigger market positively affected LeBron’s fan appeal. -

NBA.Com: Fan Night Crew Goes Courtside for Cavs-Hawks Dec. 29
12/18/2009 NBA.com: Fan Night crew goes courtsi… NBA TEAMS TICKETS GLOBAL NBA D-LEAGUE WNBA ENE-BE-A Get New s & Offers Login NEWS SCORES & SCHEDULES VIDEO PLAYERS STANDINGS STATISTICS FANTASY FAN STUFF PHOTOS MOBILE TV LEAGUE PASS STORE LATEST HEADLINES - NBA NEWS RSS Feeds E-New s Sign Up Add Widget EJ, Kevin McHale and C-Webb will announce their first live game for NBA TV on Dec. 29. NBA TV SEARCH NEWS Fan Night crew goes courtside for Cavs-Hawks Dec. 29 Posted Dec 17 2009 3:50PM Sponsored Links | what's this? NBA TV announced Thursday that its popular Fan Night studio crew of Ernie Johnson, Kevin McHale and Chris EXPOSED: The Acai Berry Scam? Webber will announce its first game for the network when the Cleveland Cavaliers and the Atlanta Hawks meet Want To Use Acai Berry? Do Not Use. Read This at Philips Arena in Atlanta on Tuesday, Dec. 29 at 7 p.m. (ET). Johnson will call play-by-play with McHale and Warning. Webber providing analysis, and Craig Sager serving as the sideline reporter. w w w .New s15TV.com For this special Fan Night telecast, NBA TV has selected the matchup. All NBA Fan Makes $127/Hr! nba.com/2009/news/…/fannight.atlanta/ 1/3 12/18/2009 NBA.com: Fan Night crew goes courtsi… other Tuesday night NBA TV games are selected by fans through an online $127/hr Part-Time Jobs Available. Requirements: Just vote on NBA.com. a Computer! w w w .PACourierNew s.com NBA TV's Fan Night has experienced a 239 percent increase in fan voting this season, including a record-breaking 180,000 votes for the Dec. -
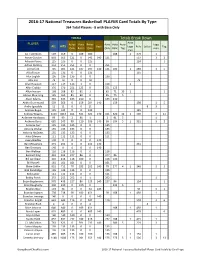
2016-17 National Treasures Basketball PLAYER Card Totals by Type 364 Total Players - 8 with Base Only
2016-17 National Treasures Basketball PLAYER Card Totals By Type 364 Total Players - 8 with Base Only TOTALS Totals Break Down Auto PLAYER Autos Auto Relics Auto Auto Auto Logo ALL HITS Base Logo Relic Letter Tag Only Relics Only Only Relic Tag man man A.J. Hammons 569 569 0 189 380 188 1 379 1 Aaron Gordon 803 663 121 0 542 140 121 537 3 2 Adreian Payne 125 125 0 0 125 124 1 Adrian Dantley 251 251 251 0 0 251 Al Horford 745 605 121 187 297 140 121 186 1 289 3 5 Al Jefferson 135 135 0 0 135 135 Alex English 136 136 136 0 0 136 Alex Len 79 79 0 0 79 79 Allan Houston 117 117 116 1 0 116 1 Allen Crabbe 376 376 251 125 0 251 125 Allen Iverson 168 168 85 82 1 85 71 10 1 1 Alonzo Mourning 165 165 85 80 0 85 75 5 Alvan Adams 345 345 135 210 0 135 210 Andre Drummond 503 363 0 159 204 140 159 198 1 5 Andre Iguodala 11 11 0 0 11 8 3 Andrew Bogut 135 135 0 0 135 135 Andrew Wiggins 1153 1013 161 331 521 140 161 320 10 1 507 3 11 Anfernee Hardaway 99 99 2 96 1 2 91 5 1 Anthony Davis 685 545 99 110 336 140 99 104 5 1 331 3 2 Antoine Carr 135 135 135 0 0 135 Antoine Walker 135 135 135 0 0 135 Antonio McDyess 135 135 135 0 0 135 Artis Gilmore 111 111 111 0 0 111 Avery Bradley 140 0 0 0 0 140 Ben McLemore 371 231 0 0 231 140 231 Ben Simmons 140 0 0 0 0 140 Ben Wallace 116 116 116 0 0 116 Bernard King 333 333 247 86 0 247 86 Bill Laimbeer 216 216 116 100 0 116 100 Bill Russell 161 161 161 0 0 161 Blake Griffin 852 712 78 282 352 140 78 277 4 1 346 3 3 Bob Dandridge 135 135 135 0 0 135 Bob Lanier 111 111 111 0 0 111 Bobby Portis 253 253 252 0 1 252 1 Bojan Bogdanovic 578 438 227 86 125 140 227 86 124 1 Brad Daugherty 230 230 0 230 0 225 5 Bradley Beal 174 34 0 0 34 140 30 3 1 Brandon Ingram 738 738 98 189 451 98 188 1 450 1 Brandon Jennings 140 0 0 0 0 140 Brandon Knight 643 643 116 0 527 116 518 3 6 Brandon Rush 4 4 0 0 4 4 Brice Johnson 640 640 0 189 451 188 1 450 1 Brook Lopez 625 485 0 0 485 140 479 6 Bryn Forbes 140 140 140 0 0 140 Buddy Hield 837 837 232 189 416 232 188 1 415 1 C.J. -

Brilliant Bryant Energizes Lakers Push
SPORTS CHINA DAILY WEDNESDAY MARCH 28, 2007 23 TOPSHOT Brilliant Bryant energizes Lakers push Maradona movie set for Italian release ROME: A movie biopic based on the rise and fall of Argentine football Kobe scoring consistently high to keep legend Diego Maradona is set to be released in cinemas throughout his team on course for playoff berth Italy on Friday. Directed by Marco Risi, Maradona La LOS ANGELES: Los Angeles Lakers the court.” Mano di Dio, or The Hand of God, the superstar Kobe Bryant, stung by two Even more important, however, phrase the Argentine used to explain National Basketball Association sus- is that Bryant’s heroics have turned how he scored a controversial goal pensions, has responded by writing things around for a Lakers team that against England with his hand in the himself into the record books. had fallen to 33-32 as they battled to 1986 World Cup quarter-fi nals, takes Last week Bryant joined Wilt overcome injuries to four key players. in different phases of the player’s life Chamberlain as the only player in Bryant’s 65-point outburst against including his drug problems. NBA history to record four or more Portland on March 16 saw the team Risi said that he wanted to show the straight games of 50 points or more. end a seven-game losing streak. humanity of a player regarded as In the process he turned in per- “If we don’t win games now, we one of the all-time greats, but who formances of 65 and 60 points, tying miss the playoffs, which means we’re has battled drugs and ill health. -

Racism in the Ron Artest Fight
UCLA UCLA Entertainment Law Review Title Flagrant Foul: Racism in "The Ron Artest Fight" Permalink https://escholarship.org/uc/item/4zr6d8wt Journal UCLA Entertainment Law Review, 13(1) ISSN 1073-2896 Author Williams, Jeffrey A. Publication Date 2005 DOI 10.5070/LR8131027082 Peer reviewed eScholarship.org Powered by the California Digital Library University of California Flagrant Foul: Racism in "The Ron Artest Fight" by Jeffrey A. Williams* "There's a reason. But I don't think anybody ought to be surprised, folks. I really don't think anybody ought to be surprised. This is the hip-hop culture on parade. This is gang behavior on parade minus the guns. That's what the culture of the NBA has become." - Rush Limbaugh1 "Do you really want to go there? Do I have to? .... I think it's fair to say that the NBA was the first sport that was widely viewed as a black sport. And whatever the numbers ultimately are for the other sports, the NBA will always be treated a certain way because of that. Our players are so visible that if they have Afros or cornrows or tattoos- white or black-our consumers pick it up. So, I think there are al- ways some elements of race involved that affect judgments about the NBA." - NBA Commissioner David Stern2 * B.A. in History & Religion, Columbia University, 2002, J.D., Columbia Law School, 2005. The author is currently an associate in the Manhattan office of Milbank Tweed Hadley & McCloy. The views reflected herein are entirely those of the author alone. -

Rosters Set for 2014-15 Nba Regular Season
ROSTERS SET FOR 2014-15 NBA REGULAR SEASON NEW YORK, Oct. 27, 2014 – Following are the opening day rosters for Kia NBA Tip-Off ‘14. The season begins Tuesday with three games: ATLANTA BOSTON BROOKLYN CHARLOTTE CHICAGO Pero Antic Brandon Bass Alan Anderson Bismack Biyombo Cameron Bairstow Kent Bazemore Avery Bradley Bojan Bogdanovic PJ Hairston Aaron Brooks DeMarre Carroll Jeff Green Kevin Garnett Gerald Henderson Mike Dunleavy Al Horford Kelly Olynyk Jorge Gutierrez Al Jefferson Pau Gasol John Jenkins Phil Pressey Jarrett Jack Michael Kidd-Gilchrist Taj Gibson Shelvin Mack Rajon Rondo Joe Johnson Jason Maxiell Kirk Hinrich Paul Millsap Marcus Smart Jerome Jordan Gary Neal Doug McDermott Mike Muscala Jared Sullinger Sergey Karasev Jannero Pargo Nikola Mirotic Adreian Payne Marcus Thornton Andrei Kirilenko Brian Roberts Nazr Mohammed Dennis Schroder Evan Turner Brook Lopez Lance Stephenson E'Twaun Moore Mike Scott Gerald Wallace Mason Plumlee Kemba Walker Joakim Noah Thabo Sefolosha James Young Mirza Teletovic Marvin Williams Derrick Rose Jeff Teague Tyler Zeller Deron Williams Cody Zeller Tony Snell INACTIVE LIST Elton Brand Vitor Faverani Markel Brown Jeffery Taylor Jimmy Butler Kyle Korver Dwight Powell Cory Jefferson Noah Vonleh CLEVELAND DALLAS DENVER DETROIT GOLDEN STATE Matthew Dellavedova Al-Farouq Aminu Arron Afflalo Joel Anthony Leandro Barbosa Joe Harris Tyson Chandler Darrell Arthur D.J. Augustin Harrison Barnes Brendan Haywood Jae Crowder Wilson Chandler Caron Butler Andrew Bogut Kentavious Caldwell- Kyrie Irving Monta Ellis