A Graphical User Interface (GUI) Input-Based Algorithm to Automate Generation of Multi-State Models for Release-Recapture Studies
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Command Line Interface Specification Windows
Command Line Interface Specification Windows Online Backup Client version 4.3.x 1. Introduction The CloudBackup Command Line Interface (CLI for short) makes it possible to access the CloudBackup Client software from the command line. The following actions are implemented: backup, delete, dir en restore. These actions are described in more detail in the following paragraphs. For all actions applies that a successful action is indicated by means of exit code 0. In all other cases a status code of 1 will be used. 2. Configuration The command line client needs a configuration file. This configuration file may have the same layout as the configuration file for the full CloudBackup client. This configuration file is expected to reside in one of the following folders: CLI installation location or the settings folder in the CLI installation location. The name of the configuration file must be: Settings.xml. Example: if the CLI is installed in C:\Windows\MyBackup\, the configuration file may be in one of the two following locations: C:\Windows\MyBackup\Settings.xml C:\Windows\MyBackup\Settings\Settings.xml If both are present, the first form has precedence. Also the customer needs to edit the CloudBackup.Console.exe.config file which is located in the program file directory and edit the following line: 1 <add key="SettingsFolder" value="%settingsfilelocation%" /> After making these changes the customer can use the CLI instruction to make backups and restore data. 2.1 Configuration Error Handling If an error is found in the configuration file, the command line client will issue an error message describing which value or setting or option is causing the error and terminate with an exit value of 1. -

Attacker Antics Illustrations of Ingenuity
ATTACKER ANTICS ILLUSTRATIONS OF INGENUITY Bart Inglot and Vincent Wong FIRST CONFERENCE 2018 2 Bart Inglot ◆ Principal Consultant at Mandiant ◆ Incident Responder ◆ Rock Climber ◆ Globetrotter ▶ From Poland but live in Singapore ▶ Spent 1 year in Brazil and 8 years in the UK ▶ Learning French… poor effort! ◆ Twitter: @bartinglot ©2018 FireEye | Private & Confidential 3 Vincent Wong ◆ Principal Consultant at Mandiant ◆ Incident Responder ◆ Baby Sitter ◆ 3 years in Singapore ◆ Grew up in Australia ©2018 FireEye | Private & Confidential 4 Disclosure Statement “ Case studies and examples are drawn from our experiences and activities working for a variety of customers, and do not represent our work for any one customer or set of customers. In many cases, facts have been changed to obscure the identity of our customers and individuals associated with our customers. ” ©2018 FireEye | Private & Confidential 5 Today’s Tales 1. AV Server Gone Bad 2. Stealing Secrets From An Air-Gapped Network 3. A Backdoor That Uses DNS for C2 4. Hidden Comment That Can Haunt You 5. A Little Known Persistence Technique 6. Securing Corporate Email is Tricky 7. Hiding in Plain Sight 8. Rewriting Import Table 9. Dastardly Diabolical Evil (aka DDE) ©2018 FireEye | Private & Confidential 6 AV SERVER GONE BAD Cobalt Strike, PowerShell & McAfee ePO (1/9) 7 AV Server Gone Bad – Background ◆ Attackers used Cobalt Strike (along with other malware) ◆ Easily recognisable IOCs when recorded by Windows Event Logs ▶ Random service name – also seen with Metasploit ▶ Base64-encoded script, “%COMSPEC%” and “powershell.exe” ▶ Decoding the script yields additional PowerShell script with a base64-encoded GZIP stream that in turn contained a base64-encoded Cobalt Strike “Beacon” payload. -

Powershell Integration with Vmware View 5.0
PowerShell Integration with VMware® View™ 5.0 TECHNICAL WHITE PAPER PowerShell Integration with VMware View 5.0 Table of Contents Introduction . 3 VMware View. 3 Windows PowerShell . 3 Architecture . 4 Cmdlet dll. 4 Communication with Broker . 4 VMware View PowerCLI Integration . 5 VMware View PowerCLI Prerequisites . 5 Using VMware View PowerCLI . 5 VMware View PowerCLI cmdlets . 6 vSphere PowerCLI Integration . 7 Examples of VMware View PowerCLI and VMware vSphere PowerCLI Integration . 7 Passing VMs from Get-VM to VMware View PowerCLI cmdlets . 7 Registering a vCenter Server . .. 7 Using Other VMware vSphere Objects . 7 Advanced Usage . 7 Integrating VMware View PowerCLI into Your Own Scripts . 8 Scheduling PowerShell Scripts . 8 Workflow with VMware View PowerCLI and VMware vSphere PowerCLI . 9 Sample Scripts . 10 Add or Remove Datastores in Automatic Pools . 10 Add or Remove Virtual Machines . 11 Inventory Path Manipulation . 15 Poll Pool Usage . 16 Basic Troubleshooting . 18 About the Authors . 18 TECHNICAL WHITE PAPER / 2 PowerShell Integration with VMware View 5.0 Introduction VMware View VMware® View™ is a best-in-class enterprise desktop virtualization platform. VMware View separates the personal desktop environment from the physical system by moving desktops to a datacenter, where users can access them using a client-server computing model. VMware View delivers a rich set of features required for any enterprise deployment by providing a robust platform for hosting virtual desktops from VMware vSphere™. Windows PowerShell Windows PowerShell is Microsoft’s command line shell and scripting language. PowerShell is built on the Microsoft .NET Framework and helps in system administration. By providing full access to COM (Component Object Model) and WMI (Windows Management Instrumentation), PowerShell enables administrators to perform administrative tasks on both local and remote Windows systems. -

Linux-PATH.Pdf
http://www.linfo.org/path_env_var.html PATH Definition PATH is an environmental variable in Linux and other Unix-like operating systems that tells the shell which directories to search for executable files (i.e., ready-to-run programs ) in response to commands issued by a user. It increases both the convenience and the safety of such operating systems and is widely considered to be the single most important environmental variable. Environmental variables are a class of variables (i.e., items whose values can be changed) that tell the shell how to behave as the user works at the command line (i.e., in a text-only mode) or with shell scripts (i.e., short programs written in a shell programming language). A shell is a program that provides the traditional, text-only user interface for Unix-like operating systems; its primary function is to read commands that are typed in at the command line and then execute (i.e., run) them. PATH (which is written with all upper case letters) should not be confused with the term path (lower case letters). The latter is a file's or directory's address on a filesystem (i.e., the hierarchy of directories and files that is used to organize information stored on a computer ). A relative path is an address relative to the current directory (i.e., the directory in which a user is currently working). An absolute path (also called a full path ) is an address relative to the root directory (i.e., the directory at the very top of the filesystem and which contains all other directories and files). -

Path Howto Path Howto
PATH HOWTO PATH HOWTO Table of Contents PATH HOWTO..................................................................................................................................................1 Esa Turtiainen etu@dna.fi.......................................................................................................................1 1. Introduction..........................................................................................................................................1 2. Copyright.............................................................................................................................................1 3. General.................................................................................................................................................1 4. Init........................................................................................................................................................1 5. Login....................................................................................................................................................1 6. Shells....................................................................................................................................................1 7. Changing user ID.................................................................................................................................1 8. Network servers...................................................................................................................................1 -

When Powerful SAS Meets Powershell
PharmaSUG 2018 - Paper QT-06 ® TM When Powerful SAS Meets PowerShell Shunbing Zhao, Merck & Co., Inc., Rahway, NJ, USA Jeff Xia, Merck & Co., Inc., Rahway, NJ, USA Chao Su, Merck & Co., Inc., Rahway, NJ, USA ABSTRACT PowerShell is an MS Windows-based command shell for direct interaction with an operating system and its task automation. When combining the powerful SAS programming language and PowerShell commands/scripts, we can greatly improve our efficiency and accuracy by removing many trivial manual steps in our daily routine work as SAS programmers. This paper presents five applications we developed for process automation. 1) Automatically convert RTF files in a folder into PDF files, all files or a selection of them. Installation of Adobe Acrobat printer is not a requirement. 2) Search the specific text of interest in all files in a folder, the file format could be RTF or SAS Source code. It is very handy in situations like meeting urgent FDA requests when there is a need to search required information quickly. 3) Systematically back up all existing files including the ones in subfolders. 4) Update the attributes of a selection of files with ease, i.e., change all SAS code and their corresponding output including RTF tables and SAS log in a production environment to read only after database lock. 5) Remove hidden temporary files in a folder. It can clean up and limit confusion while delivering the whole output folder. Lastly, the SAS macros presented in this paper could be used as a starting point to develop many similar applications for process automation in analysis and reporting activities. -

Command Line Interface (Shell)
Command Line Interface (Shell) 1 Organization of a computer system users applications graphical user shell interface (GUI) operating system hardware (or software acting like hardware: “virtual machine”) 2 Organization of a computer system Easier to use; users applications Not so easy to program with, interactive actions automate (click, drag, tap, …) graphical user shell interface (GUI) system calls operating system hardware (or software acting like hardware: “virtual machine”) 3 Organization of a computer system Easier to program users applications with and automate; Not so convenient to use (maybe) typed commands graphical user shell interface (GUI) system calls operating system hardware (or software acting like hardware: “virtual machine”) 4 Organization of a computer system users applications this class graphical user shell interface (GUI) operating system hardware (or software acting like hardware: “virtual machine”) 5 What is a Command Line Interface? • Interface: Means it is a way to interact with the Operating System. 6 What is a Command Line Interface? • Interface: Means it is a way to interact with the Operating System. • Command Line: Means you interact with it through typing commands at the keyboard. 7 What is a Command Line Interface? • Interface: Means it is a way to interact with the Operating System. • Command Line: Means you interact with it through typing commands at the keyboard. So a Command Line Interface (or a shell) is a program that lets you interact with the Operating System via the keyboard. 8 Why Use a Command Line Interface? A. In the old days, there was no choice 9 Why Use a Command Line Interface? A. -
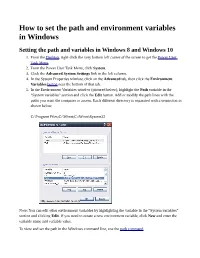
How to Set the Path and Environment Variables in Windows
How to set the path and environment variables in Windows Setting the path and variables in Windows 8 and Windows 10 1. From the Desktop, right-click the very bottom left corner of the screen to get the Power User Task Menu. 2. From the Power User Task Menu, click System. 3. Click the Advanced System Settings link in the left column. 4. In the System Properties window, click on the Advanced tab, then click the Environment Variables button near the bottom of that tab. 5. In the Environment Variables window (pictured below), highlight the Path variable in the "System variables" section and click the Edit button. Add or modify the path lines with the paths you want the computer to access. Each different directory is separated with a semicolon as shown below. C:\Program Files;C:\Winnt;C:\Winnt\System32 Note: You can edit other environment variables by highlighting the variable in the "System variables" section and clicking Edit. If you need to create a new environment variable, click New and enter the variable name and variable value. To view and set the path in the Windows command line, use the path command. Setting the path and variables in Windows Vista and Windows 7 1. From the Desktop, right-click the Computer icon and select Properties. If you don't have a Computer icon on your desktop, click the Start button, right-click the Computer option in the Start menu, and select Properties. 2. Click the Advanced System Settings link in the left column. 3. In the System Properties window, click on the Advanced tab, then click the Environment Variables button near the bottom of that tab. -

Operating Systems Homework Assignment 2
Operating Systems Homework Assignment 2 Preparation For this homework assignment, you need to get familiar with a Linux system (Ubuntu, Fedora, CentOS, etc.). There are two options to run Linux on your Desktop (or Laptop) computer: 1. Run a copy of a virtual machine freely available on-line in your own PC environment using Virtual Box. Create your own Linux virtual machine (Linux as a guest operating system) in Windows. You may consider installing MS Windows as a guest OS in Linux host. OS-X can host Linux and/or Windows as guest Operating systems by installing Virtual Box. 2. Or on any hardware system that you can control, you need to install a Linux system (Fedora, CentOS Server, Ubuntu, Ubuntu Server). Tasks to Be Performed • Write the programs listed (questions from Q1 to Q6), run the program examples, and try to answer the questions. Reference for the Assignment Some useful shell commands for process control Command Descriptions & When placed at the end of a command, execute that command in the background. Interrupt and stop the currently running process program. The program remains CTRL + "Z" stopped and waiting in the background for you to resume it. Bring a command in the background to the foreground or resume an interrupted program. fg [%jobnum] If the job number is omitted, the most recently interrupted or background job is put in the foreground. Place an interrupted command into the background. bg [%jobnum] If the job number is omitted, the most recently interrupted job is put in the background. jobs List all background jobs. -

The Complete Guide to Powershell Punctuation
The Complete Guide to PowerShell Punctuation Does not include special characters in globs (about_Wildcards) or regular expressions (about_Regular_Expressions) as those are separate “languages”. Green items are placeholders indicating where you insert either a single word/character or, with an ellipsis, a more complex expression. Symbol What it is Explanation Symbol What it is Explanation <enter> line break Allowed between statements, within strings, after these <#... Multi-line Everything between the opening and closing tokens— carriage separators [ | , ; = ] and—as of V3—these [ . :: ]. comment which may span multiple lines—is a comment. return Also allowed after opening tokens [ { [ ( ' " ] . #> Not allowed most anywhere else. call operator Forces the next thing to be interpreted as a command statement Optional if you always use line breaks after statements; & even if it looks like a string. So while either Get- ; required to put multiple statements on one line, e.g. semicolon separator ampersand ChildItem or & Get-ChildItem do the same thing, $a = 25; Write-Output $a "Program Files\stuff.exe" just echoes the string name variable prefix $ followed by letters, numbers, or underscores specifies a literal, while & "Program Files\stuff.exe" will $ variable name, e.g. $width. Letters and numbers are not execute it. dollar sign limited to ASCII; some 18,000+ Unicode chars are eligible. (a) line As the last character on a line, lets you continue on the variable prefix To embed any other characters in a variable name enclose ` continuation next line where PowerShell would not normally allow a ${...} it in braces, e.g ${save-items}. See about_Variables. back tick; line break. Make sure it is really last—no trailing spaces! grave accent See about_Escape_Characters path accessor Special case: ${drive-qualified path} lets you, e.g., ${path} store to (${C:tmp.txt}=1,2,3) or retrieve from (b) literal Precede a dollar sign to avoid interpreting the following character characters as a variable name; precede a quote mark ($data=${C:tmp.txt}) a file. -

Dell Command | Powershell Provider Version 2.3 User's Guide
Dell Command | PowerShell Provider Version 2.3 User's Guide April 2020 Rev. A00 Notes, cautions, and warnings NOTE: A NOTE indicates important information that helps you make better use of your product. CAUTION: A CAUTION indicates either potential damage to hardware or loss of data and tells you how to avoid the problem. WARNING: A WARNING indicates a potential for property damage, personal injury, or death. © 2020 Dell Inc. or its subsidiaries. All rights reserved. Dell, EMC, and other trademarks are trademarks of Dell Inc. or its subsidiaries. Other trademarks may be trademarks of their respective owners. Contents Chapter 1: Introduction to Dell Command | PowerShell Provider 2.3..............................................5 Document scope and intended audience.......................................................................................................................5 Other documents you may need......................................................................................................................................5 What’s new in this release.................................................................................................................................................5 Chapter 2: System requirements and prerequisites for Dell Command | PowerShell Provider 2.3............................................................................................................................................. 7 Supported Dell platforms.................................................................................................................................................. -

Lecture 22 Systems Programming Process Control
Lecture 22 Systems Programming Process Control A process is defined as an instance of a program that is currently running. A uni processor system can still execute multiple processes giving the appearance of a multi- processor machine. A call to a program spawns a process. If a mail program is called by n users then n processes or instances are created and executed by the unix system. Many operating systems including windows and unix executes many processes at the same time. When a program is called, a process is created and a process ID is issued. The process ID is given by the function getpid() defined in <unistd.h>. The prototype for pid( ) is given by #include < unistd.h > pid_t getpid(void); In a uni-processor machine, each process takes turns running and for a short duration, a process takes time interval called a timeslice. The unix command ps can be used to list all current process status. ps PID TTY TIME CMD 10150 pts/16 00:00:00 csh 31462 pts/16 00:00:00 ps The command ps lists the process ID (PID), the terminal name(TTY), the amount of time the process has used so far(TIME) and the command it is executing(CMD). Ps command only displays the current user processes. But we can get all the processes with the flag (- a) and in long format with flag (-l) ps –a ps -l ps -al Information provided by each process may include the following. PID The process ID in integer form PPID The parent process ID in integer form STAT The state of the process TIME CPU time used by the process (in seconds) TT Control terminal of the process COMMAND The user command that started the process Copyright @ 2008 Ananda Gunawardena Each process has a process ID that can be obtained using the getpid() a system call declared in unistd.h.