Adaptive Federated Learning in Resource Constrained Edge Computing Systems
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Explainable Federated Learning for Taxi Travel Time Prediction
Explainable Federated Learning for Taxi Travel Time Prediction Jelena Fiosina a Institute of Informatics, Clausthal Technical University, Julius-Albert Str. 4, D-38678, Clausthal-Zellerfeld, Germany Keywords: FCD Trajectories, Traffic, Travel Time Prediction, Federated Learning, Explainability. Abstract: Transportation data are geographically scattered across different places, detectors, companies, or organisations and cannot be easily integrated under data privacy and related regulations. The federated learning approach helps process these data in a distributed manner, considering privacy concerns. The federated learning archi- tecture is based mainly on deep learning, which is often more accurate than other machine learning models. However, deep-learning-based models are intransparent unexplainable black-box models, which should be explained for both users and developers. Despite the fact that extensive studies have been carried out on investigation of various model explanation methods, not enough solutions for explaining federated models exist. We propose an explainable horizontal federated learning approach, which enables processing of the dis- tributed data while adhering to their privacy, and investigate how state-of-the-art model explanation methods can explain it. We demonstrate this approach for predicting travel time on real-world floating car data from Brunswick, Germany. The proposed approach is general and can be applied for processing data in a federated manner for other prediction and classification tasks. 1 INTRODUCTION transparent. This feature of AI-driven systems com- plicates the user acceptance and can be troublesome Most real-world data are geographically scattered even for model developers. across different places, companies, or organisations, Therefore, the contemporary AI technologies and, unfortunately, cannot be easily integrated under should be capable of processing these data in a de- data privacy and related regulations. -

Exploiting Shared Representations for Personalized Federated Learning
Exploiting Shared Representations for Personalized Federated Learning Liam Collins 1 Hamed Hassani 2 Aryan Mokhtari 1 Sanjay Shakkottai 1 Abstract effective models for each client by leveraging the local com- putational power, memory, and data of all clients (McMahan Deep neural networks have shown the ability to et al., 2017). The task of coordinating between the clients extract universal feature representations from data is fulfilled by a central server that combines the models such as images and text that have been useful received from the clients at each round and broadcasts the for a variety of learning tasks. However, the updated information to them. Importantly, the server and fruits of representation learning have yet to be clients are restricted to methods that satisfy communica- fully-realized in federated settings. Although data tion and privacy constraints, preventing them from directly in federated settings is often non-i.i.d. across applying centralized techniques. clients, the success of centralized deep learning suggests that data often shares a global feature However, one of the most important challenges in federated representation, while the statistical heterogene- learning is the issue of data heterogeneity, where the under- ity across clients or tasks is concentrated in the lying data distribution of client tasks could be substantially labels. Based on this intuition, we propose a different from each other. In such settings, if the server novel federated learning framework and algorithm and clients learn a single shared model (e.g., by minimizing for learning a shared data representation across average loss), the resulting model could perform poorly for clients and unique local heads for each client. -

Architectural Patterns for the Design of Federated Learning Systems
Architectural Patterns for the Design of Federated Learning Systems a,b < a,b a,b b a,b a Sin Kit Lo , , Qinghua Lu , Liming Zhu , Hye-Young Paik , Xiwei Xu and Chen Wang aData61, CSIRO, Australia bUniversity of New South Wales, Australia ARTICLEINFO ABSTRACT Federated learning has received fast-growing interests from academia and industry to tackle the chal- Keywords: lenges of data hungriness and privacy in machine learning. A federated learning system can be viewed as a large-scale distributed system with different components and stakeholders as numerous client de- Federated Learning vices participate in federated learning. Designing a federated learning system requires software system design thinking apart from the machine learning knowledge. Although much effort has been put into Pattern federated learning from the machine learning technique aspects, the software architecture design con- Software Architecture cerns in building federated learning systems have been largely ignored. Therefore, in this paper, we present a collection of architectural patterns to deal with the design challenges of federated learning Machine Learning systems. Architectural patterns present reusable solutions to a commonly occurring problem within a Artificial Intelligence given context during software architecture design. The presented patterns are based on the results of a systematic literature review and include three client management patterns, four model management patterns, three model training patterns, and four model aggregation patterns. The patterns are asso- ciated to the particular state transitions in a federated learning model lifecycle, serving as a guidance for effective use of the patterns in the design of federated learning systems. Central Model 1. Introduction Server aggregation Federated Learning Overview The ever-growing use of big data systems, industrial-scale IoT platforms, and smart devices contribute to the exponen- tial growth in data dimensions [30]. -

A Survey on Federated Learning and Its Applications for Accelerating Industrial Internet of Things
A Survey on Federated Learning and its Applications for Accelerating Industrial Internet of Things Jiehan Zhou Shouhua Zhang Qinghua Lu [email protected] [email protected] [email protected] University of Oulu University of Oulu CSIRO, Data61 13 Garden Street Eveleigh SYDNEY Wenbin Dai Min Chen Xin Liu [email protected] [email protected] [email protected] Shanghai Jiao Tong University Huazhong Univ. of Science China University of and Technology, China Petroleum Huadong Susanna Pirttikangas Yang Shi Weishan Zhang [email protected] [email protected] [email protected] University of Oulu University of Victoria China University of Petroleum Huadong - Qingdao Campus Enrique Herrera-Viedma [email protected] (IoT) is being widely applied in mobile services. There are few Abstract—Federated learning (FL) brings collaborative reports on applying large-scale data and deep learning (DL) to intelligence into industries without centralized training data to implement large-scale enterprise intelligence. One of the accelerate the process of Industry 4.0 on the edge computing level. reasons is lack of machine learning (ML) approaches which can FL solves the dilemma in which enterprises wish to make the use make distributed learning available while not infringing the of data intelligence with security concerns. To accelerate user’s data privacy. Clearly, FL trains a model by enabling the industrial Internet of things with the further leverage of FL, existing achievements on FL are developed from three aspects: 1) individual devices to act as local learners and send local model define terminologies and elaborate a general framework of FL for parameters to a federal server (defined in section 2) instead of accommodating various scenarios; 2) discuss the state-of-the-art training data. -

A Federated Learning Framework for On-Device Anomaly Data Detection
Federated Learning for Internet of Things Tuo Zhang*, Chaoyang He*, Tianhao Ma, Lei Gao, Mark Ma, Salman Avestimehr Univerisity of Southern California Los Angeles, California, USA ABSTRACT anomaly-detection-based intrusion detection in IoT devices. IoTDe- Federated learning can be a promising solution for enabling IoT fender [2] is another similar framework but obtains a personalized cybersecurity (i.e., anomaly detection in the IoT environment) model by fine-tuning the global model trained with FL.[4] evaluates while preserving data privacy and mitigating the high communica- FL-based anomaly detection framework with learning tasks such tion/storage overhead (e.g., high-frequency data from time-series as aggressive driving detection and human activity recognition. [8] sensors) of centralized over-the-cloud approaches. In this paper, to further proposes an attention-based CNN-LSTM model to detect further push forward this direction with a comprehensive study anomalies in an FL manner, and reduces the communication cost in both algorithm and system design, we build FedIoT platform by using Top-: gradient compression. Recently, [15] even evaluates that contains FedDetect algorithm for on-device anomaly data the impact of malicious clients under the setting of FL-based anom- detection and a system design for realistic evaluation of federated aly detection. However, these works do not evaluate the efficacy learning on IoT devices. Furthermore, the proposed FedDetect of FL in a wide range of attack types and lack system design and learning framework improves the performance by utilizing a local performance analysis in a real IoT platform. adaptive optimizer (e.g., Adam) and a cross-round learning rate To further push forward the research in FL-based IoT cybersecu- scheduler. -

Selective Federated Transfer Learning Using Representation Similarity
Selective Federated Transfer Learning using Representation Similarity Tushar Semwal1, Haofan Wang2, Chinnakotla Krishna Teja Reddy3 { 1The University of Edinburgh, 2Carnegie Mellon University, 3GE Healthcare, 1;2;3OpenMined} { [email protected], 2 [email protected], [email protected] } Abstract Transfer Learning (TL) has achieved significant developments in the past few years. However, the majority of work on TL assume implicit access to both the target and source datasets, which limits its application in the context of Federated Learning (FL), where target (client) datasets are usually not directly accessible. In this paper, we address the problem of source model selection in TL for federated scenarios. We propose a simple framework, called Selective Federated Transfer Learning (SFTL), to select the best pre-trained models which provide a positive performance gain when their parameters are transferred on to a new task. We leverage the concepts from representation similarity to compare the similarity of the client model and the source models and provide a method which could be augmented to existing FL algorithms to improve both the communication cost and the accuracy of client models. 1 Introduction The conventional deep learning (DL) approaches involve first collecting data (for instance, images or text) from various sources such as smartphones, and storage devices, and then training a Deep Neural Network (DNN) using this centrally aggregated data. Though this centralised form of architecture is relatively practical to implement and provides full control, the act of gathering data in third-party private servers raises serious privacy concerns. Further, with the Internet of Things (IoT) entering a new era of development, International Data Corporation is estimating a total of 41.6 billion connected IoT devices generating 79.4 zettabytes of data in 2025 [1]. -

ASSIST-Iot Technical Report #2
This project has received funding from the European’s Union Horizon 2020 research innovation programme under Grant Agreement No. 957258 Architecture for Scalable, Self-*, human-centric, Intelligent, Secure, and Tactile next generation IoT ASSIST-IoT Technical Report #2 Sunday-FL – Developing Open Source Platform for Federated Learning Piotr Niedziela, Anastasiya Danilenka, Dominik Kolasa, Maria Ganzha, Marcin Paprzycki, Kumar Nalinaksh 2021 Emerging Trends in Industry 4.0 (ETI 4.0) Sunday-FL – Developing Open Source Platform for Federated Learning Piotr Niedziela, Anastasiya Danilenka, Maria Ganzha, Marcin Paprzycki Kumar Nalinaksh Dominik Kolasa Systems Research Institute Institute of Management and Department of Mathematics and Information Science Polish Academy of Sciences Technical Sciences Warsaw University of Technology fi[email protected] Warsaw Management University Abstract—Since its inception, in approximately 2017, federated The latter should be understood as follows. While it is possible learning became an area of intensive research. Obviously, such that computing takes place within a network of workstations, research requires tools that can be used for experimentation. loosely connected using PVM [4], or Condor middleware [5], Here, the biggest industrial players proposed their own platforms, but these platforms are anchored in tools that they “promote”. all nodes havw a single owner and should be treated jointly Moreover, they are mainly “all-in-one” solutions, aimed at as a part of single “virtual computer”. facilitating the federate learning process, rather than supporting Keeping this in mind, let us reflect on changes that took research “about it”. Taking this into account, we have decided place within last few years (and are still ongoing). -

Efficient and Less Centralized Federated Learning
Efficient and Less Centralized Federated Learning Li Chou?, Zichang Liu? ( ), Zhuang Wang, and Anshumali Shrivastava Department of Computer Science Rice University, Houston TX, USA flchou,zl71,zw50,[email protected] Abstract. With the rapid growth in mobile computing, massive amounts of data and computing resources are now located at the edge. To this end, Federated learning (FL) is becoming a widely adopted distributed machine learning (ML) paradigm, which aims to harness this expanding skewed data locally in order to develop rich and informative models. In centralized FL, a collection of devices collaboratively solve a ML task under the coordination of a central server. However, existing FL frame- works make an over-simplistic assumption about network connectivity and ignore the communication bandwidth of the different links in the network. In this paper, we present and study a novel FL algorithm, in which devices mostly collaborate with other devices in a pairwise man- ner. Our nonparametric approach is able to exploit network topology to reduce communication bottlenecks. We evaluate our approach on various FL benchmarks and demonstrate that our method achieves 10× better communication efficiency and around 8% increase in accuracy compared to the centralized approach. Keywords: Machine Learning · Federated Learning · Distributed Sys- tems. 1 Introduction The rapid growth in mobile computing on edge devices, such as smartphones and tablets, has led to a significant increase in the availability of distributed computing resources and data sources. These devices are equipped with ever more powerful sensors, higher computing power, and storage capability, which is contributing to the next wave of massive data in a decentralized manner. -

Fedcv: a Federated Learning Framework for Diverse Computer Vision Tasks
FedCV: A Federated Learning Framework for Diverse Computer Vision Tasks Chaoyang He1, Alay Dilipbhai Shah1, Zhenheng Tang2, Di Fan1 Adarshan Naiynar Sivashunmugam1, Keerti Bhogaraju1, Mita Shimpi1, Li Shen3, Xiaowen Chu2, Mahdi Soltanolkotabi1, Salman Avestimehr1 University of Southern California1, Hong Kong Baptist University2, Tencent AI Lab3 {chaoyang.he, avestime}@usc.edu Abstract Federated Learning (FL) is a distributed learning paradigm that can learn a global or personalized model from decentralized datasets on edge devices. However, in the computer vision domain, model performance in FL is far behind centralized training due to the lack of exploration in diverse tasks with a unified FL framework. FL has rarely been demonstrated effectively in advanced computer vision tasks such as object detection and image segmentation. To bridge the gap and facilitate the development of FL for computer vision tasks, in this work, we propose a feder- ated learning library and benchmarking framework, named FedCV, to evaluate FL on the three most representative com- puter vision tasks: image classification, image segmentation, and object detection. We provide non-I.I.D. benchmarking Figure 1. Our philosophy of federated learning on computer vision: datasets, models, and various reference FL algorithms. Our connecting the algorithmic FL research and CV application-drive benchmark study suggests that there are multiple challenges research with an unified research framework. that deserve future exploration: centralized training tricks may not be directly applied to FL; the non-I.I.D. dataset actually downgrades the model accuracy to some degree in sonalization [75, 14, 42, 55, 28, 20, 10], system efficiency different tasks; improving the system efficiency of federated (communication and computation) [23], robustness to at- training is challenging given the huge number of parame- tacks [67, 2, 15, 1, 68, 7, 58, 13, 7, 56, 49], and privacy ters and the per-client memory cost. -

Federated Learning: Opportunities and Challenges
Federated Learning: Opportunities and Challenges Priyanka Mary Mammen University of Massachusetts, Amherst [email protected] ABSTRACT patient information to a central server can reveal sensitive infor- Federated Learning (FL) is a concept first introduced by Google in mation to the public with several repercussions. In such scenarios, 2016, in which multiple devices collaboratively learn a machine Federated Learning can be better option.Federated Learning is a col- learning model without sharing their private data under the super- laborative learning technique among devices/organizations, where vision of a central server. This offers ample opportunities in critical the model parameters from local models are shared and aggregated domains such as healthcare, finance etc, where it is risky to share instead of sharing their local data. private user information to other organisations or devices. While The notion of Federated Learning is introduced by Google in FL appears to be a promising Machine Learning (ML) technique 2016, where they first applied in google keyboard to collabora- to keep the local data private, it is also vulnerable to attacks like tively learn from several android phones [24]. Given that FL can other ML models. Given the growing interest in the FL domain, be applied to any edge device, it has the potential to revolutionize this report discusses the opportunities and challenges in federated critical domains such as healthcare, transportation, finance, smart learning. home etc. The most prominent example is when the researchers and medical practitioners from different parts of the world collabo- CCS CONCEPTS ratively developed an AI pandemic engine for COVID-19 diagnosis from chest scans [1]. -
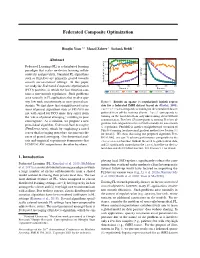
Federated Composite Optimization
Federated Composite Optimization Honglin Yuan 12 Manzil Zaheer 3 Sashank Reddi 3 Abstract Federated Learning (FL) is a distributed learning paradigm that scales on-device learning collab- oratively and privately. Standard FL algorithms such as FEDAVG are primarily geared towards smooth unconstrained settings. In this paper, we study the Federated Composite Optimization (FCO) problem, in which the loss function con- tains a non-smooth regularizer. Such problems arise naturally in FL applications that involve spar- sity, low-rank, monotonicity, or more general con- Figure 1. Results on sparse (`1-regularized) logistic regres- straints. We first show that straightforward exten- sion for a federated fMRI dataset based on (Haxby, 2001). sions of primal algorithms such as FEDAVG are centralized corresponds to training on the centralized dataset not well-suited for FCO since they suffer from gathered from all the training clients. local corresponds to the “curse of primal averaging,” resulting in poor training on the local data from only one training client without convergence. As a solution, we propose a new communication. FEDAVG (@) corresponds to running FEDAVG al- gorithms with subgradient in lieu of SGD to handle the non-smooth primal-dual algorithm, Federated Dual Averaging `1-regularizer. FEDMID is another straightforward extension of (FEDDUALAVG), which by employing a novel FEDAVG running local proximal gradient method (see Section 3.1 server dual averaging procedure circumvents the for details). We show that using our proposed algorithm FED- curse of primal averaging. Our theoretical anal- DUALAVG, one can 1) achieve performance comparable to the ysis and empirical experiments demonstrate that centralized baseline without the need to gather client data, FEDDUALAVG outperforms the other baselines. -

Advances and Open Problems in Federated Learning
Advances and Open Problems in Federated Learning Peter Kairouz7* H. Brendan McMahan7∗ Brendan Avent21 Aurelien´ Bellet9 Mehdi Bennis19 Arjun Nitin Bhagoji13 Kallista Bonawitz7 Zachary Charles7 Graham Cormode23 Rachel Cummings6 Rafael G.L. D’Oliveira14 Hubert Eichner7 Salim El Rouayheb14 David Evans22 Josh Gardner24 Zachary Garrett7 Adria` Gascon´ 7 Badih Ghazi7 Phillip B. Gibbons2 Marco Gruteser7;14 Zaid Harchaoui24 Chaoyang He21 Lie He 4 Zhouyuan Huo 20 Ben Hutchinson7 Justin Hsu25 Martin Jaggi4 Tara Javidi17 Gauri Joshi2 Mikhail Khodak2 Jakub Konecnˇ y´7 Aleksandra Korolova21 Farinaz Koushanfar17 Sanmi Koyejo7;18 Tancrede` Lepoint7 Yang Liu12 Prateek Mittal13 Mehryar Mohri7 Richard Nock1 Ayfer Ozg¨ ur¨ 15 Rasmus Pagh7;10 Hang Qi7 Daniel Ramage7 Ramesh Raskar11 Mariana Raykova7 Dawn Song16 Weikang Song7 Sebastian U. Stich4 Ziteng Sun3 Ananda Theertha Suresh7 Florian Tramer` 15 Praneeth Vepakomma11 Jianyu Wang2 Li Xiong5 Zheng Xu7 Qiang Yang8 Felix X. Yu7 Han Yu12 Sen Zhao7 1Australian National University, 2Carnegie Mellon University, 3Cornell University, 4Ecole´ Polytechnique Fed´ erale´ de Lausanne, 5Emory University, 6Georgia Institute of Technology, 7Google Research, 8Hong Kong University of Science and Technology, 9INRIA, 10IT University of Copenhagen, 11Massachusetts Institute of Technology, 12Nanyang Technological University, 13Princeton University, 14Rutgers University, 15Stanford University, 16University of California Berkeley, 17 University of California San Diego, 18University of Illinois Urbana-Champaign, 19University of Oulu, 20University of Pittsburgh, 21University of Southern California, 22University of Virginia, 23University of Warwick, 24University of Washington, 25University of Wisconsin–Madison arXiv:1912.04977v3 [cs.LG] 9 Mar 2021 Abstract Federated learning (FL) is a machine learning setting where many clients (e.g. mobile devices or whole organizations) collaboratively train a model under the orchestration of a central server (e.g.